二叉堆与树状数组

本章将介绍两种树形结构——二叉堆和树状数组。

大学生活是忙碌而丰富多彩的，有大量的任务需要完成，例如作业、实验、完成论文、兼职工作等。这些任务都是不得不做的，而且每个任务都有对应的截止日期。对于一个有拖延症的学生来说，他每次决定完成哪些任务，一定会选择最接近截止日期的任务，因为这个任务最为紧迫，优先级最高。

对于这种可以查询最大或最小值，可以插入新的元素，可以删除最大最小值的集合容器，被称为优先队列。通过使用二叉堆实现优先队列，可以较高效率地完成插入和查询操作。

而树状数组可以很方便的维护序列的前缀和等信息。因此，可以使用树状数组高效完成单点修改、区间求和的任务。虽然之后介绍的线段树也可以完成这些任务，而且时间复杂度都是O(logn)，但是树状数组运行时间的常数更小，所需空间更小，代码也更加短小精悍。

二叉堆

堆（Heap）是一类数据结构，它们拥有树状结构，且能够保证父节点比子节点大（或小）。当根节点保存堆中最大值时，称为大根堆；反之，则称为小根堆。

二叉堆是最简单、常用的堆，是一棵符合堆的性质的完全二叉树。它可以实现 O(log⁡n) 地插入或删除某个值，并且 O(1) 地查询最大（或最小）值。

作为一棵完全二叉树，二叉堆完全可以用一个数组实现

下面是关于最大堆的一些代码实现，有注释

//1.top操作
int top()
{
    return w[1];
    //返回堆顶也就是最大值
}
void modify(int x)
{
if(x==1||w[x]<w[x/2])
{
    return ;
    //就是你已经到达根顶了，或者你已经小于你的父节点了
    //这样就行了实际上
}
swap(w[x],w[x/2]);
//这也正是没有达到上述情况，那么你就要交换
modify(x/2);
//交换完继续处理上一个节点
//递归处理
}
void push(int x)
{
    w[++tot]=x;//加入元素直接在尾部进行加入
    modify(tot);//自底向上修复
}
void repair(int x)
{
if(x*2>tot)
{
    return ;
    //已经到达叶子节点，和上个modify操作一样
}
int tar=2*x;
if(x*2+1<=tot)
{
    tar=w[x*2]>w[x*2+1]?x*2:x*2+1;
}
if(w[x]<w[tar])
{
    swap(w[x],w[tar]);
    repair(tar);
}
}
void pop()
{
    swap(w[1],w[tot--]);
    //这一步有两个操作，第一个是交换头尾，第二个是删除尾部
   //接下来我们要修复头部
   repair(1); 
}

堆排序：来自华南理工大学2023年选拔赛2第一题

新生杯录取

题目背景

一年一度的新生杯结束啦！

题目描述

新生杯强者如云，12题里最多有人过了8题，并且同时有N个人过了8题，我们希望在这N个人中挑前K位(最多100位)选手入队，按照ICPC赛制，罚时少的选手排名会更靠前。

现在给到cp这N个选手的罚时，保证数据随机排列，请帮他求出前K位选手的罚时。

输入格式

第一行两个整数$N$和$K$

第二行$N$个整数，表示每名选手的罚时

保证：

$1\le N\le 10^7$

$1\le K \le 100$

$K\le N$

每名选手的总罚时都是非负整数，且罚时都 $<10^9$，可能会有多个人罚时相同

输出格式

一行$K$个整数，升序地输出罚时最少的$K$个选手的罚时

样例 #1

样例输入 #1

1 2	4 2 50 20 10 70

样例输出 #1

10 20

提示

如果你是C++选手，并且酷爱cin/cout，不妨按照以下方式，将一行神奇代码贴入你的main()函数下，可以加速数据读入

int main(){
std::ios_base::sync_with_stdio(false);std::cin.tie(0);
	//内容 
}

代码如下：

不解释，代码很易懂

#include<bits/stdc++.h>
using namespace std;
priority_queue<int >q;
int a[120];
int main()
{
	ios_base::sync_with_stdio(false);std::cin.tie(0);
int n,k;
cin>>n>>k;	
int x;
for(int i=1;i<=k;i++)
{
	cin>>x;
	q.push(x);
}
for(int i=k+1;i<=n;i++)
{
	cin>>x;
	if(x<q.top())
	{
		q.pop();
		q.push(x);
	}
}
int n2=0;
while(!q.empty())
{
	int c=q.top();
	a[n2++]=c;
	q.pop();
}
n2--;
for(int i=n2;i>=0;i--)
{
	cout<<a[i]<<' ';
}
}

介绍以下STL的堆实现

priority_queue

包含头文件#include <queue>

//升序队列
priority_queue <int,vector<int>,greater<int> > q;
//降序队列
priority_queue <int,vector<int>,less<int> >q;
//less相当于正常的

#include <stdio.h>
#include <queue>
using namespace std;
int main()
{
    priority_queue<int> q;
    q.push(3);
    q.push(4);
    q.push(1);
    cout<<q.top();
    return 0;
}

（1）push()

push(x) 将令 x 入队，时间复杂度为 O(logN)，其中 N 为当前优先队列中的元素个数。

（2）top()

top() 可以获得队首元素（即堆顶元素），时间复杂度为 O(1) 。

（3）pop()

pop() 令队首元素（即堆顶元素）出队，时间复杂度为 O(logN)，其中 N 为当前优先队列中的元素个数。

（4）empty()

empty() 检测优先队列是否为空，返回 true 则空，返回 false 则非空。时间复杂度为 O(1)。

（5）size()

size() 返回优先队列内元素的个数，时间复杂度为 O(1)。

【模板】堆

题目描述

给定一个数列，初始为空，请支持下面三种操作：

给定一个整数 $x$，请将 $x$ 加入到数列中。
输出数列中最小的数。
删除数列中最小的数（如果有多个数最小，只删除 $1$ 个）。

输入格式

第一行是一个整数，表示操作的次数 $n$。
接下来 $n$ 行，每行表示一次操作。每行首先有一个整数 $op$ 表示操作类型。

若 $op = 1$，则后面有一个整数 $x$，表示要将 $x$ 加入数列。
若 $op = 2$，则表示要求输出数列中的最小数。
若 $op = 3$，则表示删除数列中的最小数。如果有多个数最小，只删除 $1$ 个。

输出格式

对于每个操作 $2$，输出一行一个整数表示答案。

样例 #1

样例输入 #1

样例输出 #1

1
2

2
5

提示

【数据规模与约定】

对于 $30\%$ 的数据，保证 $n \leq 15$。
对于 $70\%$ 的数据，保证 $n \leq 10^4$。
对于 $100\%$ 的数据，保证 $1 \leq n \leq 10^6$，$1 \leq x \lt 2^{31}$，$op \in \{1, 2, 3\}$。

#include<bits/stdc++.h>
using namespace std;
const int N=1e7;
int w[N];
int tot;
//一个是数组，一个是最后一个节点所在位置
//1.top操作
int top()
{
    return w[1];
    //返回堆顶也就是最大值
}
void modify(int x)
{
if(x==1||w[x]<w[x/2])
{
    return ;
    //就是你已经到达根顶了，或者你已经小于你的父节点了
    //这样就行了实际上
}
swap(w[x],w[x/2]);
//这也正是没有达到上述情况，那么你就要交换
modify(x/2);
//交换完继续处理上一个节点
//递归处理
}
void push(int x)
{
    w[++tot]=x;//加入元素直接在尾部进行加入
    modify(tot);//自底向上修复
}
void repair(int x)
{
if(x*2>tot)
{
    return ;
    //已经到达叶子节点，和上个modify操作一样
}
int tar=2*x;
if(x*2+1<=tot)
{
    tar=w[x*2]>w[x*2+1]?x*2:x*2+1;
}
if(w[x]<w[tar])
{
    swap(w[x],w[tar]);
    repair(tar);
}
}
void pop()
{
    swap(w[1],w[tot--]);
    //这一步有两个操作，第一个是交换头尾，第二个是删除尾部
   //接下来我们要修复头部
   repair(1); 
}
int main()
{
int n;
cin>>n;
while(n--)
{
    int op;
    int x;
    cin>>op;
if(op==1)
{
    cin>>x;
    push(-x);
}
else if(op==2)
{
    cout<<-top()<<'\n';
}
else
{
    pop();
}
}
return 0;
}

黑匣子

题目描述

Black Box 是一种原始的数据库。它可以储存一个整数数组，还有一个特别的变量 $i$。最开始的时候 Black Box 是空的．而 $i=0$。这个 Black Box 要处理一串命令。

命令只有两种：

ADD(x)：把 $x$ 元素放进 Black Box;
GET：$i$ 加 $1$，然后输出 Black Box 中第 $i$ 小的数。

记住：第 $i$ 小的数，就是 Black Box 里的数的按从小到大的顺序排序后的第 $i$ 个元素。

我们来演示一下一个有11个命令的命令串。（如下表所示）

序号	操作	$i$	数据库	输出
1	`ADD(3)`	$0$	$3$	/
2	`GET`	$1$	$3$	$3$
3	`ADD(1)`	$1$	$1,3$	/
4	`GET`	$2$	$1,3$	$3$
5	`ADD(-4)`	$2$	$-4,1,3$	/
6	`ADD(2)`	$2$	$-4,1,2,3$	/
7	`ADD(8)`	$2$	$-4,1,2,3,8$	/
8	`ADD(-1000)`	$2$	$-1000,-4,1,2,3,8$	/
9	`GET`	$3$	$-1000,-4,1,2,3,8$	$1$
10	`GET`	$4$	$-1000,-4,1,2,3,8$	$2$
11	`ADD(2)`	$4$	$-1000,-4,1,2,2,3,8$	/

现在要求找出对于给定的命令串的最好的处理方法。ADD 命令共有 $m$ 个，GET 命令共有 $n$ 个。现在用两个整数数组来表示命令串：

$a_1,a_2,\cdots,a_m$：一串将要被放进 Black Box 的元素。例如上面的例子中 $a=[3,1,-4,2,8,-1000,2]$。
$u_1,u_2,\cdots,u_n$：表示第 $u_i$ 个元素被放进了 Black Box 里后就出现一个 GET 命令。例如上面的例子中 $u=[1,2,6,6]$ 。输入数据不用判错。

输入格式

第一行两个整数 $m$ 和 $n$，表示元素的个数和 GET 命令的个数。

第二行共 $m$ 个整数，从左至右第 $i$ 个整数为 $a_i$，用空格隔开。

第三行共 $n$ 个整数，从左至右第 $i$ 个整数为 $u_i$，用空格隔开。

输出格式

输出 Black Box 根据命令串所得出的输出串，一个数字一行。

样例 #1

样例输入 #1

1
2
3

7 4
3 1 -4 2 8 -1000 2
1 2 6 6

样例输出 #1

提示

数据规模与约定

对于 $30\%$ 的数据，$1 \leq n,m \leq 10^{4}$。
对于 $50\%$ 的数据，$1 \leq n,m \leq 10^{5}$。
对于 $100\%$ 的数据，$1 \leq n,m \leq 2 \times 10^{5},|a_i| \leq 2 \times 10^{9}$，保证 $u$ 序列单调不降。

对顶堆

对顶堆是由一个大顶堆和一个小顶堆组合而成的数据结构，与传统堆维护最大数不同，对顶堆用于动态维护第k大的数。在对顶堆中，小根堆位于大根堆的上方，要保证小根堆的所有数始终比大根堆大。

对顶堆由一个大根堆与一个小根堆组成: 小根堆维护大值即前k大的值（包含第k个）; 大根堆维护小值即比第k大数小的其他数。

维护：当小根堆的大小小于k时，不断将大根堆堆顶元素取出并插入小根堆，直到小根堆的大小等于k; 当小根堆的大小大于k时，不断将小根堆堆顶元素取出并插入大根堆，直到小根堆的大小等于k；

插入元素：

若插入的元素大于等于小根堆堆顶元素，则将其插入小根堆，否则将其插入大根堆，然后维护对顶堆；

查询第k大元素

查询第k大元素：小根堆堆顶元素即为所求；

删除第k大元素

删除第k大元素：删除小根堆堆顶元素，然后维护对顶堆；

#include<bits/stdc++.h>
using namespace std;
int a[200005];
int main(){    
    priority_queue<int>A;
    priority_queue<int,vector<int>,greater<int>>B;
    int n,m,r=1,q;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    for(int i=1;i<=m;i++){
        cin>>q;
        for(int j=r;j<=q;j++){
            A.push(a[j]);
            if(A.size()==i)B.push(A.top()),A.pop();
        }
        r=q+1;
        cout<<B.top()<<'\n';
        A.push(B.top());
        B.pop();
    }
    return 0;
}

[NOIP2004 提高组] 合并果子 / [USACO06NOV] Fence Repair G

题目描述

在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。

每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过 $n-1$ 次合并之后，就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为 $1$ ，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。

例如有 $3$ 种果子，数目依次为 $1$ ， $2$ ， $9$ 。可以先将 $1$ 、 $2$ 堆合并，新堆数目为 $3$ ，耗费体力为 $3$ 。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为 $12$ ，耗费体力为 $12$ 。所以多多总共耗费体力 $=3+12=15$ 。可以证明 $15$ 为最小的体力耗费值。

输入格式

共两行。
第一行是一个整数 $n(1\leq n\leq 10000)$ ，表示果子的种类数。

第二行包含 $n$ 个整数，用空格分隔，第 $i$ 个整数 $a_i(1\leq a_i\leq 20000)$ 是第 $i$ 种果子的数目。

输出格式

一个整数，也就是最小的体力耗费值。输入数据保证这个值小于 $2^{31}$ 。

样例 #1

样例输入 #1

1
2

3 
1 2 9

样例输出 #1

提示

对于 $30\%$ 的数据，保证有 $n \le 1000$：

对于 $50\%$ 的数据，保证有 $n \le 5000$；

对于全部的数据，保证有 $n \le 10000$。

#include<bits/stdc++.h>
using namespace std;
const int N=1e7;
#define rep(i,a,n) for(int i=a;i<=n;i++)
priority_queue <int,vector<int>,greater<int> >q;
int main()
{
int n,x,y;
int ans=0;
int cost;
cin>>n;
rep(i,1,n)
{
    cin>>x;
    q.push(x);
}
while(q.size()>1)
{
    x=q.top();
q.pop();
    y=q.top();
q.pop();
cost =x+y;
q.push(cost);
ans+=cost;
}
cout<<ans;


}

[NOI2015] 荷马史诗

题目背景

追逐影子的人，自己就是影子 —— 荷马

题目描述

Allison 最近迷上了文学。她喜欢在一个慵懒的午后，细细地品上一杯卡布奇诺，静静地阅读她爱不释手的《荷马史诗》。但是由《奥德赛》和《伊利亚特》组成的鸿篇巨制《荷马史诗》实在是太长了，Allison 想通过一种编码方式使得它变得短一些。

一部《荷马史诗》中有 $n$ 种不同的单词，从 $1$ 到 $n$ 进行编号。其中第 $i$ 种单词出现的总次数为 $w_i$。Allison 想要用 $k$ 进制串 $s_i$ 来替换第 $i$ 种单词，使得其满足如下要求：

对于任意的 $1\leq i, j\leq n$ ，$i\ne j$ ，都有：$s_i$ 不是 $s_j$ 的前缀。

现在 Allison 想要知道，如何选择 $s_i$，才能使替换以后得到的新的《荷马史诗》长度最小。在确保总长度最小的情况下，Allison 还想知道最长的 $s_i$ 的最短长度是多少？

一个字符串被称为 $k$ 进制字符串，当且仅当它的每个字符是 $0$ 到 $k-1$ 之间（包括 $0$ 和 $k-1$ ）的整数。

字符串 $str1$ 被称为字符串 $str2$ 的前缀，当且仅当：存在 $1 \leq t\leq m$ ，使得 $str1 = str2[1..t]$。其中，$m$ 是字符串 $str2$ 的长度，$str2[1..t]$ 表示 $str2$ 的前 $t$ 个字符组成的字符串。

输入格式

输入的第 $1$ 行包含 $2$ 个正整数 $n, k$ ，中间用单个空格隔开，表示共有 $n$ 种单词，需要使用 $k$ 进制字符串进行替换。

接下来 $n$ 行，第 $i + 1$ 行包含 $1$ 个非负整数 $w_i$，表示第 $i$ 种单词的出现次数。

输出格式

输出包括 $2$ 行。

第 $1$ 行输出 $1$ 个整数，为《荷马史诗》经过重新编码以后的最短长度。

第 $2$ 行输出 $1$ 个整数，为保证最短总长度的情况下，最长字符串 $s_i$ 的最短长度。

样例 #1

样例输入 #1

样例输出 #1

1
2

12
2

样例 #2

样例输入 #2

样例输出 #2

1
2

36
3

提示

【样例解释】

样例 1 解释

用 $X(k)$ 表示 $X$ 是以 $k$ 进制表示的字符串。

一种最优方案：令 $00(2)$ 替换第 $1$ 种单词， $01(2)$ 替换第 2 种单词， $10(2)$ 替换第 $3$ 种单词，$11(2)$ 替换第 $4$ 种单词。在这种方案下，编码以后的最短长度为：

$1 × 2 + 1 × 2 + 2 × 2 + 2 × 2 = 12$

最长字符串 $s_i$ 的长度为 $2$ 。

一种非最优方案：令 $000(2)$ 替换第 $1$ 种单词，$001(2)$ 替换第 $2$ 种单词，$01(2)$ 替换第 $3$ 种单词，$1(2)$ 替换第 $4$ 种单词。在这种方案下，编码以后的最短长度为：

$1 × 3 + 1 × 3 + 2 × 2 + 2 × 1 = 12$

最长字符串 $s_i$ 的长度为 $3$ 。与最优方案相比，文章的长度相同，但是最长字符串的长度更长一些。

样例 2 解释

一种最优方案：令 $000(3)$ 替换第 $1$ 种单词，$001(3)$ 替换第 $2$ 种单词，$01(3)$ 替换第 $3$ 种单词， $02(3)$ 替换第 $4$ 种单词， $1(3)$ 替换第 5 种单词， $2(3)$ 替换第 $6$ 种单词。

【数据规模与约定】

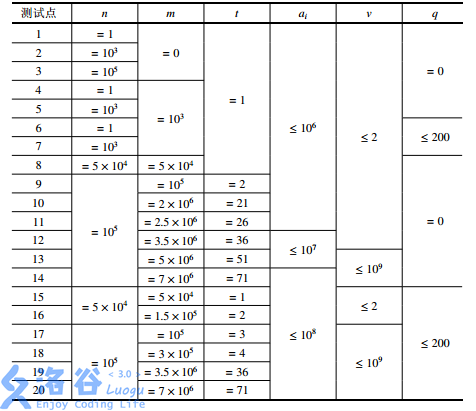
所有测试数据的范围和特点如下表所示（所有数据均满足 $0 < w_i \leq 10^{11}$）：

测试点编号	$n$ 的规模	$k$ 的规模	备注
$1$	$n=3$	$k=2$
$2$	$n=5$	$k=2$
$3$	$n=16$	$k=2$	所有 $w_i$ 均相等
$4$	$n=1\,000$	$k=2$	$w_i$ 在取值范围内均匀随机
$5$	$n=1\,000$	$k=2$
$6$	$n=100\,000$	$k=2$
$7$	$n=100\,000$	$k=2$	所有 $w_i$ 均相等
$8$	$n=100\,000$	$k=2$
$9$	$n=7$	$k=3$
$10$	$n=16$	$k=3$	所有 $w_i$ 均相等
$11$	$n=1\,001$	$k=3$	所有 $w_i$ 均相等
$12$	$n=99\,999$	$k=4$	所有 $w_i$ 均相等
$13$	$n=100\,000$	$k=4$
$14$	$n=100\,000$	$k=4$
$15$	$n=1\,000$	$k=5$
$16$	$n=100\,000$	$k=7$	$w_i$ 在取值范围内均匀随机
$17$	$n=100\,000$	$k=7$
$18$	$n=100\,000$	$k=8$	$w_i$ 在取值范围内均匀随机
$19$	$n=100\,000$	$k=9$
$20$	$n=100\,000$	$k=9$

【提示】

选手请注意使用 64 位整数进行输入输出、存储和计算。

【评分方式】

对于每个测试点：

若输出文件的第 $1$ 行正确，得到该测试点 $40\%$ 的分数；
若输出文件完全正确，得到该测试点 $100\%$ 的分数。

前置知识：哈夫曼树

哈夫曼树：带权路径长度WPL最短的多叉树（最优多叉树）构造这种树的算法最早是由哈夫曼(Huffman)1952年提出，这种树在信息检索中很有用。

每次挑选权值最小的两棵树进行合并即可得到哈夫曼树（二叉做法）

本题是k叉哈夫曼树

因此要取k个

#include<bits/stdc++.h>
using namespace std;
const int N=1e7;
#define rep(i,a,n) for(ll i=a;i<=n;i++)
using ll=long long ;
struct node
{
    ll w,h;
};
bool operator<(node a,node b)
{
    if(a.w!=b.w)
{
    return a.w>b.w;
}
return a.h>b.h;
}
//先长度后高度
priority_queue<node>q;
//单调队列
int main()
{
int n,k;
ll ans=0;
ll wi;
cin>>n>>k;
rep(i,1,n)
{
    cin>>wi;
    q.push(node{wi,1});
}
    //扔进去，一开始高度都是1
if((n-1)%(k-1)!=0)
{
    rep(i,1,k-1-(n-1)%(k-1))
    {
        q.push(node{0,1});
        //补足不够的点，因为要能整除，权值赋值为0就好，空点
    }
}
while(q.size()!=1)
  //终止条件
{
    node tmp;
    ll sum=0;
    ll maxh=0;
    //高度初始化
    rep(i,1,k)
    {
        tmp=q.top();
      sum+=tmp.w;
      maxh=max(maxh,tmp.h);
      q.pop();  
    }
    //挑选K个点
    ans+=sum;
    //加上和
    q.push(node{sum,maxh+1});
    //进行这个插入新节点
}
cout<<ans<<"\n"<<q.top().h-1;
}

[NOIP2016 提高组] 蚯蚓

题目背景

NOIP2016 提高组 D2T2

题目描述

本题中，我们将用符号 $\lfloor c \rfloor$ 表示对 $c$ 向下取整，例如：$\lfloor 3.0 \rfloor = \lfloor 3.1 \rfloor = \lfloor 3.9 \rfloor = 3$。

蛐蛐国最近蚯蚓成灾了！隔壁跳蚤国的跳蚤也拿蚯蚓们没办法，蛐蛐国王只好去请神刀手来帮他们消灭蚯蚓。

蛐蛐国里现在共有 $n$ 只蚯蚓（$n$ 为正整数）。每只蚯蚓拥有长度，我们设第 $i$ 只蚯蚓的长度为 $a_i\,(i=1,2,\dots,n)$，并保证所有的长度都是非负整数（即：可能存在长度为 $0$ 的蚯蚓）。

每一秒，神刀手会在所有的蚯蚓中，准确地找到最长的那一只（如有多个则任选一个）将其切成两半。神刀手切开蚯蚓的位置由常数 $p$（是满足 $0 < p < 1$ 的有理数）决定，设这只蚯蚓长度为 $x$，神刀手会将其切成两只长度分别为 $\lfloor px \rfloor$ 和 $x - \lfloor px \rfloor$ 的蚯蚓。特殊地，如果这两个数的其中一个等于 $0$，则这个长度为 $0$ 的蚯蚓也会被保留。此外，除了刚刚产生的两只新蚯蚓，其余蚯蚓的长度都会增加 $q$（是一个非负整常数）。

蛐蛐国王知道这样不是长久之计，因为蚯蚓不仅会越来越多，还会越来越长。蛐蛐国王决定求助于一位有着洪荒之力的神秘人物，但是救兵还需要 $m$ 秒才能到来……（$m$ 为非负整数）

蛐蛐国王希望知道这 $m$ 秒内的战况。具体来说，他希望知道：

$m$ 秒内，每一秒被切断的蚯蚓被切断前的长度（有 $m$ 个数）；
$m$ 秒后，所有蚯蚓的长度（有 $n + m$ 个数）。

蛐蛐国王当然知道怎么做啦！但是他想考考你……

输入格式

第一行包含六个整数 $n,m,q,u,v,t$，其中：$n,m,q$ 的意义见【问题描述】；$u,v,t$ 均为正整数；你需要自己计算 $p=u / v$（保证 $0 < u < v$）；$t$ 是输出参数，其含义将会在【输出格式】中解释。

第二行包含 $n$ 个非负整数，为 $a_1, a_2, \dots, a_n$，即初始时 $n$ 只蚯蚓的长度。

同一行中相邻的两个数之间，恰好用一个空格隔开。

保证 $1 \leq n \leq 10^5$，$0 \leq m \leq 7 \times 10^6$，$0 < u < v \leq 10^9$，$0 \leq q \leq 200$，$1 \leq t \leq 71$，$0 \leq a_i \leq 10^8$。

输出格式

第一行输出 $\left \lfloor \frac{m}{t} \right \rfloor$ 个整数，按时间顺序，依次输出第 $t$ 秒，第 $2t$ 秒，第 $3t$ 秒，……被切断蚯蚓（在被切断前）的长度。

第二行输出 $\left \lfloor \frac{n+m}{t} \right \rfloor$ 个整数，输出 $m$ 秒后蚯蚓的长度；需要按从大到小的顺序，依次输出排名第 $t$，第 $2t$，第 $3t$，……的长度。

同一行中相邻的两个数之间，恰好用一个空格隔开。即使某一行没有任何数需要输出，你也应输出一个空行。

请阅读样例来更好地理解这个格式。

样例 #1

样例输入 #1

1 2	3 7 1 1 3 1 3 3 2

样例输出 #1

1 2	3 4 4 4 5 5 6 6 6 6 5 5 4 4 3 2 2

样例 #2

样例输入 #2

1 2	3 7 1 1 3 2 3 3 2

样例输出 #2

1 2	4 4 5 6 5 4 3 2

样例 #3

样例输入 #3

1 2	3 7 1 1 3 9 3 3 2

样例输出 #3

1
2

//空行
2

提示

样例解释 1

在神刀手到来前：$3$ 只蚯蚓的长度为 $3,3,2$。

$1$ 秒后：一只长度为 $3$ 的蚯蚓被切成了两只长度分别为$1$ 和 $2$ 的蚯蚓，其余蚯蚓的长度增加了 $1$。最终 $4$ 只蚯蚓的长度分别为 $(1,2),4,3$。括号表示这个位置刚刚有一只蚯蚓被切断。

$2$ 秒后：一只长度为 $4$ 的蚯蚓被切成了 $1$ 和 $3$。$5$ 只蚯蚓的长度分别为：$2,3,(1,3),4$。

$3$ 秒后：一只长度为 $4$ 的蚯蚓被切断。$6$ 只蚯蚓的长度分别为：$3,4,2,4,(1,3)$。

$4$ 秒后：一只长度为 $4$ 的蚯蚓被切断。$7$ 只蚯蚓的长度分别为：$4,(1,3),3,5,2,4$。

$5$ 秒后：一只长度为 $5$ 的蚯蚓被切断。$8$ 只蚯蚓的长度分别为：$5,2,4,4,(1,4),3,5$。

$6$ 秒后：一只长度为 $5$ 的蚯蚓被切断。$9$ 只蚯蚓的长度分别为：$(1,4),3,5,5,2,5,4,6$。

$7$ 秒后：一只长度为 $6$ 的蚯蚓被切断。$10$ 只蚯蚓的长度分别为：$2,5,4,6,6,3,6,5,(2,4)$。所以，$7$ 秒内被切断的蚯蚓的长度依次为 $3,4,4,4,5,5,6$。$7$ 秒后，所有蚯蚓长度从大到小排序为 $6,6,6,5,5,4,4,3,2,2$。

样例解释 2

这个数据中只有 $t=2$ 与上个数据不同。只需在每行都改为每两个数输出一个数即可。

虽然第一行最后有一个 $6$ 没有被输出，但是第二行仍然要重新从第二个数再开始输出。

样例解释 3

这个数据中只有 $t=9$ 与上个数据不同。

注意第一行没有数要输出，但也要输出一个空行。

数据范围

//本题思路就是你每次要加太麻烦了，你就在要加的时候加，然后维护原来的相对大小就行了
//这里用3个队列来模拟优先队列，因为每次分成两份嘛，加进去即可，这里是决定保证正确性的
//因此只需要排序一个队列，其他两个队列放尸体就行
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+20;
#define rep(i,a,n) for(ll i=a;i<=n;i++)
using ll=long long ;
ll n, m, q, u, v, t, tmp;
ll a[N];
bool cmp(ll a,ll b)
{
    return a>b;
}
//保证从大到小
const ll inf= 2100000000;
//用来比较用的
queue<ll>q1,q2,q3;
//3个队列
ll x,y;
//中间值，往下看
ll findmax()
    //找3个队列的最大值
{
    ll x,x1,x2,x3;
    if(!q1.empty())
    {
        x1=q1.front();
    }
    else
    {
        x1=-inf;
    }
    if (!q2.empty())
    {
        x2 = q2.front();
    }
    else
    {
        x2 = -inf;
    }
    if (!q3.empty())
    {
        x3 = q3.front();
    }
    else
    {
        x3 = -inf;
    }
    if(x1>x2&&x1>x3)
    {
        x=x1;
        q1.pop();
    }
    else if(x2>x3)
    {
        x=x2;
        q2.pop();
    }
    else
    {
        x=x3;
        q3.pop();
    }
return x;
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    //关闭同步
  cin>>n>>m>>q>>u>>v>>t;
    //输入
  rep(i,1,n)
  {
    cin>>a[i];
  }
    //输入
  sort(a+1,a+1+n,cmp);
    //从大到小排序
   rep(i,1,n)
   {
    q1.push(a[i]);
   }
    //扔进队列
   rep(i,1,m)
   {
    x=findmax()+q*(i-1);
       //这时候要加上，因为前面少加了i-1轮
    if(i%t==0)
    {
cout<<x<<' ';
        //输出
    }
    y=1.0*x*u/v;
       //切成的两半，扔进去队列
    x=x-y;
    y-=q*i;
    q2.push(y);
    x-=q*i;
       //保证正确性，多减去一轮
    q3.push(x);
   }
   cout<<'\n';
    
rep(i,1,n+m)
{
    x=findmax()+q*m;
    //每次都找最大值并加上
    if(i%t==0)
    {
        if(x==8625869)
        {
            x++;
        }
        if(x==91374031)
        {
            x--;
        }
        //依照样例编程（当时调不出来了，不知道为什么wa了1个点）
        cout<<x<<' ';     
    }
}
return 0;
}
------------------------------------------------------------------------------
    //今天看了以下应该是精度问题，改了个小地方就过了
    //本题思路就是你每次要加太麻烦了，你就在要加的时候加，然后维护原来的相对大小就行了
//这里用3个队列来模拟优先队列，因为每次分成两份嘛，加进去即可，这里是决定保证正确性的
//因此只需要排序一个队列，其他两个队列放尸体就行
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+20;
#define rep(i,a,n) for(ll i=a;i<=n;i++)
using ll=long long ;
ll n, m, q, u, v, t, tmp;
ll a[N];
bool cmp(ll a,ll b)
{
    return a>b;
}
//保证从大到小
const ll inf= 2100000000;
//用来比较用的
queue<ll>q1,q2,q3;
//3个队列
ll x,y;
//中间值，往下看
ll findmax()
    //找3个队列的最大值
{
    ll x,x1,x2,x3;
    if(!q1.empty())
    {
        x1=q1.front();
    }
    else
    {
        x1=-inf;
    }
    if (!q2.empty())
    {
        x2 = q2.front();
    }
    else
    {
        x2 = -inf;
    }
    if (!q3.empty())
    {
        x3 = q3.front();
    }
    else
    {
        x3 = -inf;
    }
    if(x1>x2&&x1>x3)
    {
        x=x1;
        q1.pop();
    }
    else if(x2>x3)
    {
        x=x2;
        q2.pop();
    }
    else
    {
        x=x3;
        q3.pop();
    }
return x;
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    //关闭同步
  cin>>n>>m>>q>>u>>v>>t;
    //输入
  rep(i,1,n)
  {
    cin>>a[i];
  }
    //输入
  sort(a+1,a+1+n,cmp);
    //从大到小排序
   rep(i,1,n)
   {
    q1.push(a[i]);
   }
    //扔进队列
   rep(i,1,m)
   {
    x=findmax()+q*(i-1);
       //这时候要加上，因为前面少加了i-1轮
    if(i%t==0)
    {
cout<<x<<' ';
        //输出
    }
    y=1.0*x/v*u;
       //切成的两半，扔进去队列
    x=x-y;
    y-=q*i;
    q2.push(y);
    x-=q*i;
       //保证正确性，多减去一轮
    q3.push(x);
   }
   cout<<'\n';
    
rep(i,1,n+m)
{
    x=findmax()+q*m;
    //每次都找最大值并加上
    if(i%t==0)
    {

        //依照样例编程（当时调不出来了，不知道为什么wa了1个点）
        cout<<x<<' ';     
    }
}
return 0;
}

中位数

题目描述

给定一个长度为 $N$ 的非负整数序列 $A$，对于前奇数项求中位数。

输入格式

第一行一个正整数 $N$。

第二行 $N$ 个正整数 $A_{1\dots N}$。

输出格式

共 $\lfloor \frac{N + 1}2\rfloor$ 行，第 $i$ 行为 $A_{1\dots 2i - 1}$ 的中位数。

样例 #1

样例输入 #1

1 2	7 1 3 5 7 9 11 6

样例输出 #1

样例 #2

样例输入 #2

1 2	7 3 1 5 9 8 7 6

样例输出 #2

提示

对于 $20\%$ 的数据，$N \le 100$；

对于 $40\%$ 的数据，$N \le 3000$；

对于 $100\%$ 的数据，$1 \le N ≤ 100000$，$0 \le A_i \le 10^9$。

//题解第一篇真的太牛了，二分插入保证单调性，直接输出（），虽然是运气好过的（）
#include <bits/stdc++.h>
using namespace std;
int n;
vector<int>a;
int main()
{
    cin>>n;
    for(int i=1,x;i<=n;i++)
    {
        cin>>x;
        a.insert(upper_bound(a.begin(),a.end(),x),x);
        if(i%2==1)
        {
        	cout<<a[(i-1)/2]<<'\n';
        }
    }
    return 0;
}

正解应该是堆，而不是二分加vector()

#include<bits/stdc++.h>
using namespace std;
int n;
int a[100100];
int mid;
priority_queue<int,vector<int>,less<int> >q1;//大根堆
priority_queue<int,vector<int>,greater<int> >q2;//小根堆
int main()
{
    cin>>n;
    cin>>a[1];
    mid=a[1];
    cout<<mid<<'\n';
    //第一个答案
    for(int i=2;i<=n;i++){
        cin>>a[i];
        if(a[i]>mid) q2.push(a[i]);
        else q1.push(a[i]);
        //小根堆里面存比较大的
        //大根堆里面存比较小的
        if(i%2==1)
        {//第奇数次加入
            while(q1.size()!=q2.size())
            {
                //在输出答案前需要对mid进行调整，如果小根堆和大根堆内元素相同，就无需处理，此时mid仍然是当前的中位数。
                if(q1.size()>q2.size())
                {
                    q2.push(mid);
                    mid=q1.top();
                    q1.pop();
                }
                //哪边大输出哪边，进入另一边，并弹出输出的
                else
                {
                    q1.push(mid);
                    mid=q2.top();
                    q2.pop();
                }
            }
            cout<<mid<<'\n';
        }
    }
    return 0;
}

最小函数值

题目描述

有 $n$ 个函数，分别为 $F_1,F_2,\dots,F_n$。定义 $F_i(x)=A_ix^2+B_ix+C_i(x\in\mathbb N*)$。给定这些 $A_i$、$B_i$ 和 $C_i$，请求出所有函数的所有函数值中最小的 $m$ 个（如有重复的要输出多个）。

输入格式

第一行输入两个正整数 $n$ 和 $m$。

以下 $n$ 行每行三个正整数，其中第 $i$ 行的三个数分别为 $A_i$、$B_i$ 和 $C_i$。

输出格式

输出将这 $n$ 个函数所有可以生成的函数值排序后的前 $m$ 个元素。这 $m$ 个数应该输出到一行，用空格隔开。

样例 #1

样例输入 #1

样例输出 #1

1	9 12 12 19 25 29 31 44 45 54

提示

数据规模与约定

对于全部的测试点，保证 $1 \leq n,m\le10000$，$1 \leq A_i\le10,B_i\le100,C_i\le10^4$。

本题的思路是优先队列，因为a,b,c都是正的，先把所有的1放进去，然后取最小的，把最小的2放进去，以此类推，不难吧（）思维难度应该还行

//怎么好奇怪的熟悉感，这个操作，先放最小的，再放次小的，好像在一道异或的紫题看到过（），这比那题好多了
//闲话少叙，开始解析
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for(int i=a;i<=n;i++)
const int N=5e6;
using ll=long long;
ll n,m;
struct node
{
	ll val;
	ll x;
	ll from;
};
bool operator <(node a,node b)
{
	return a.val>b.val;
}
//重载了
priority_queue<node>q;
//优先队列
struct hanshu
{
	int a,b,c;
}b[N];
//计入三个参数
ll jisuan(ll i,ll x)
{
return b[i].a*x*x+b[i].b*x+b[i].c;
}
//计算函数
int main()
{
	cin>>n>>m;
	rep(i,1,n)
	{
		cin>>b[i].a>>b[i].b>>b[i].c;
		q.push((node){jisuan(i,1),1,i});
        //先放1
	}

rep(i,1,m)
{
	node h=q.top();
	cout<<h.val<<' '; 
	q.pop();
	q.push((node){jisuan(h.from,h.x+1),h.x+1,h.from});	
    //放进去下一个点
}		
}

序列合并

题目描述

有两个长度为 $N$ 的单调不降序列 $A,B$，在 $A,B$ 中各取一个数相加可以得到 $N^2$ 个和，求这 $N^2$ 个和中最小的 $N$ 个。

输入格式

第一行一个正整数 $N$；

第二行 $N$ 个整数 $A_{1\dots N}$。

第三行 $N$ 个整数 $B_{1\dots N}$。

输出格式

一行 $N$ 个整数，从小到大表示这 $N$ 个最小的和。

样例 #1

样例输入 #1

1
2
3

3
2 6 6
1 4 8

样例输出 #1

3 6 7

提示

对于 $50\%$ 的数据，$N \le 10^3$。

对于 $100\%$ 的数据，$1 \le N \le 10^5$，$1 \le a_i,b_i \le 10^9$。

//推导（看题解）得到是j枚举到n/i就够了（），不过确实是显而易见把，因为再枚举确实没什么意思
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,tmp,a[100010],b[100010];
priority_queue<int,vector<int>,greater<int> > pque;
int main()
{
   cin>>n;
    for(int i=1;i<=n;++i) cin>>a[i];
    for(int i=1;i<=n;++i) cin>>b[i];
    for(int i=1;i<=n;++i)
    {
        for(int j=1;j<=n/i;++j)
        {
            pque.push(a[i]+b[j]);
        }
    }
    for(int i=1;i<=n;++i)
    {
        cout<<pque.top()<<' ';
        pque.pop();
    }
    return 0;
}

[JSOI2007] 建筑抢修

题目描述

小刚在玩 JSOI 提供的一个称之为“建筑抢修”的电脑游戏：经过了一场激烈的战斗，T 部落消灭了所有 Z 部落的入侵者。但是 T 部落的基地里已经有 $N$ 个建筑设施受到了严重的损伤，如果不尽快修复的话，这些建筑设施将会完全毁坏。现在的情况是：T 部落基地里只有一个修理工人，虽然他能瞬间到达任何一个建筑，但是修复每个建筑都需要一定的时间。同时，修理工人修理完一个建筑才能修理下一个建筑，不能同时修理多个建筑。如果某个建筑在一段时间之内没有完全修理完毕，这个建筑就报废了。你的任务是帮小刚合理的制订一个修理顺序，以抢修尽可能多的建筑。

输入格式

第一行，一个整数 $N$。

接下来 $N$ 行，每行两个整数 $T_1,T_2$ 描述一个建筑：修理这个建筑需要 $T_1$ 秒，如果在 $T_2$ 秒之内还没有修理完成，这个建筑就报废了。

输出格式

输出一个整数 $S$，表示最多可以抢修 $S$ 个建筑。

样例 #1

样例输入 #1

样例输出 #1

提示

对于 $100 \%$ 的数据，$1 \le N < 150000$，$1 \le T_1 < T_2 < 2^{31}$。

#include <bits/stdc++.h>
using ll=long long;
const int  N =150001;
using namespace std;
struct Building
{
    ll t1;
    ll t2;
}build[N];
//按照时间二进行排序，力求最短报废时间
bool cmp(Building a , Building b)
{
    return a.t2 < b.t2;
}
int n;
ll sum , ans;
priority_queue<ll >Q;    //采用优先队列维护耗时最长的建筑。
int main()
{
    cin >> n;
    for(int i = 1; i <= n; i ++)
    {
        cin >> build[i].t1 >> build[i].t2;
    }
    sort(build + 1 , build + 1 + n , cmp);
    for(int i = 1; i <= n; i ++){
        sum += build[i].t1;
        //先加入修理时间，扔进去优先队列
        Q.push(build[i].t1);
        if(sum <= build[i].t2)
        {     //如果可以修，就修。
            ans ++;
        }
        else
        {       
            //否则报废耗时最长的建筑。
            sum -= Q.top();
            Q.pop();
        }
    }
    cout << ans << "\n";

    return 0;
}

舞蹈课

题目描述

有 $n$ 个人参加一个舞蹈课。每个人的舞蹈技术由整数来决定。在舞蹈课的开始，他们从左到右站成一排。当这一排中至少有一对相邻的异性时，舞蹈技术相差最小的那一对会出列并开始跳舞。如果不止一对，那么最左边的那一对出列。一对异性出列之后，队伍中的空白按原顺序补上（即：若队伍为 ABCD，那么 BC 出列之后队伍变为 AD）。舞蹈技术相差最小即是 $a_i$ 的绝对值最小。

任务是模拟以上过程，确定跳舞的配对及顺序。

输入格式

第一行一个正整数 $n$ 表示队伍中的人数。

第二行包含 $n$ 个字符 B 或者 G，B 代表男，G 代表女。

第三行为 $n$ 个整数 $a_i$。所有信息按照从左到右的顺序给出。

输出格式

第一行一个整数表示出列的总对数 $k$。

接下来 $k$ 行，每行是两个整数。按跳舞顺序输出，两个整数代表这一对舞伴的编号（按输入顺序从左往右 $1$ 至 $n$ 编号）。请先输出较小的整数，再输出较大的整数。

样例 #1

样例输入 #1

1
2
3

4
BGBG
4 2 4 3

样例输出 #1

1
2
3

2
3 4
1 2

提示

对于 $50\%$ 的数据，$1\leq n\leq 200$。

对于 $100\%$ 的数据，$1\leq n\leq 2\times 10^5$，$1\le a_i\le 10^7$。

本题利用的是断链成环+优先队列先拿掉的思想

#include<bits/stdc++.h>
using namespace std;
#define inf 2000000000
int ans[200005][2],sum=0;
struct node//链表 
{
	int l,r,cha,xu;
	bool judge;
}a[200005];
bool operator<(node rr,node ll)//优先队列有限法则 
{
	int lll=abs(ll.cha),rrr=abs(rr.cha);
	if(rrr!=lll)
		return lll<rrr;
	else
		return ll.xu<rr.xu;
}
//比较，插值小的放前面，不然就序号小的放前面
priority_queue <node> que;
//优先队列
int main ( )
{
	int n,now,next,t=0;
	char x;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>x;
		if(x=='B') 
            a[i].judge=0;
		else 
            a[i].judge=1;
	} //0代表男性，1代表女性
	cin>>now;
	for(int i=1;i<n;i++)
	{
		cin>>next;
        //与now进行递算
		a[i].xu=i;	 		
        //自身是第几个 
		a[i].cha=next-now;
        //预处理技术值差 
		a[i].l=i-1;a[i].r=i+1;
        //预处理左右 
		que.push(a[i]);
        //扔进去队列
		now=next;
        //继续进行now的变换
	}
	a[n].r=n+1;a[n].xu=n;a[n].cha=inf;
	while(!que.empty())//开始模拟过程 
	{
		int xx=que.top().xu;
        //记录序号
        int cmp=que.top().cha;
        //记录差值
		que.pop();
        //弹出
		int yy=a[xx].r;
        //记录右边，因为插值记录的实际上是自己减去前面，因此右边的记录右边减去自己，应该是需要绝对值
		if(a[xx].cha==cmp&&a[xx].judge!=a[yy].judge&&xx!=0&&yy!=n+1)
		{
			ans[++t][0]=xx;ans[t][1]=yy;
			a[a[xx].l].cha+=a[xx].cha+a[yy].cha;
            //更新差值 
			a[a[yy].r].l=a[xx].l;
            a[a[xx].l].r=a[yy].r;
            //断链重连 
			if(a[xx].l>0&&a[yy].r<=n)
                //特判链表首尾 
				que.push(a[a[xx].l]);
            //入队列 
			a[xx].l=a[xx].r=0;a[yy].l=a[yy].r=n+1;
		}
	}
	cout<<t<<'\n';
	for(int i=1;i<=t;i++)
		cout<<ans[i][0]<<" "<<ans[i][1]<<'\n';
	return 0;
}

质量检测

题目描述

为了检测生产流水线上总共 $N$ 件产品的质量，我们首先给每一件产品打一个分数 $A$ 表示其品质，然后统计前 $M$ 件产品中质量最差的产品的分值 $Q[m] = min\{A_1, A_2, ... A_m\}$，以及第 2 至第 $M + 1$ 件的 $Q[m + 1], Q[m + 2] $... 最后统计第 $N - M + 1$ 至第 $N$ 件的 $Q[n]$。根据 $Q$ 再做进一步评估。

请你尽快求出 $Q$ 序列。

输入格式

输入共两行。

第一行共两个数 $N$、$M$，由空格隔开。含义如前述。

第二行共 $N$ 个数，表示 $N$ 件产品的质量。

输出格式

输出共 $N - M + 1$ 行。

第 1 至 $N - M + 1$ 行每行一个数，第 $i$ 行的数 $Q[i + M - 1]$。含义如前述。

样例 #1

样例输入 #1

1 2	10 4 16 5 6 9 5 13 14 20 8 12

样例输出 #1

提示

[数据范围]

30%的数据，$N \le 1000$

100%的数据，$N \le 100000$

100%的数据，$M \le N, A \le 1 000 000$

ST表模板题目

#include<bits/stdc++.h>
using namespace std;
#define re register
#define rep(i,a,n) for(re int i=a;i<=n;i++)
#define frep(i,a,n) for(re int i=a;i>=n;i--)
const int N=1e6+10;
int st[N][21];
int query(int l,int r)
{
	int k=log2(r-l+1);
	return min(st[l][k],st[r-(1<<k)+1][k]);
}
int main()
{
	ios::sync_with_stdio(0);
 cin.tie(0);
 cout.tie(0);
	int n,m;
	cin>>n>>m;
	rep(i,1,n)
	{
		cin>>st[i][0];
	}
	rep(j,1,21)
	{
		rep(i,1,n-(1<<j)+1)
		{
			st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);
		}
		
	}
	rep(i,1,n-m+1)
	{
		cout<<query(i,i+m-1)<<'\n';
	}
}

【模板】树状数组 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

将某一个数加上 $x$
求出某区间每一个数的和

输入格式

第一行包含两个正整数 $n,m$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 个整数，表示一个操作，具体如下：

1 x k 含义：将第 $x$ 个数加上 $k$
2 x y 含义：输出区间 $[x,y]$ 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 $2$ 的结果。

样例 #1

样例输入 #1

样例输出 #1

1
2

14
16

提示

【数据范围】

对于 $30\%$ 的数据，$1 \le n \le 8$，$1\le m \le 10$；
对于 $70\%$ 的数据，$1\le n,m \le 10^4$；
对于 $100\%$ 的数据，$1\le n,m \le 5\times 10^5$。

数据保证对于任意时刻，$a$ 的任意子区间（包括长度为 $1$ 和 $n$ 的子区间）和均在 $[-2^{31}, 2^{31})$ 范围内。

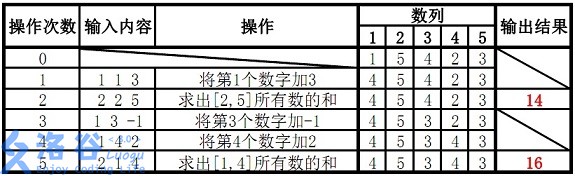
样例说明：

故输出结果14、16

以下两题详见树状数组

//直接作差版本，姑且这么说吧
#include<iostream>
using ll=long long; 
using namespace std;
int c[30000000];
int n,m;
int ans;
int lowbit(int x)
{
	return x&-x;
}
void add(int x,int k)
{
	for(int i=x;i<=n;i+=lowbit(i))
	c[i]+=k;
}
void search(int L,int R)
{
	for(int i=L-1;i;i-=lowbit(i))	
	ans-=c[i];	
	for(int i=R;i;i-=lowbit(i))
	ans+=c[i];
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		int number;
		cin>>number;
		add(i,number);
	}
	for(int i=1;i<=m;i++)
	{
		int choice,x,y;
		cin>>choice>>x>>y;
		if(choice==1)
        {
             add(x,y);
        }
		else
		{
			ans=0;
			search(x,y);
			cout<<ans<<'\n';
		}
	}
	return 0;
}

或者

//间接作差型
#include<bits/stdc++.h>
using namespace std;
int tree[30000000];
int n,m;
int lowbit(int x)
{
	return x&-x;
}
void add(int x,int y )
{
	for(int i=x;i<=n;i+=lowbit(i))
	{
		tree[i]+=y;
	}
}
int sum(int x)
{
	if(x==0)
	{
		return 0;
	}
	int ans=0;
	for(int i=x;i>0;i-=lowbit(i))
	{
		ans+=tree[i];
	}	
	return ans;
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		int a;
		cin>>a;
		add(i,a);
	}
	for(int i=1;i<=m;i++)
	{
		int x,y,z;
		cin>>x>>y>>z;
		if(x==1)
		{
			add(y,z);
		}
		if(x==2)
		{
			int end=sum(z)-sum(y-1);
			cout<<'\n';
		}
	}
	return 0;
}

【模板】树状数组 2

题目描述

如题，已知一个数列，你需要进行下面两种操作：

将某区间每一个数加上 $x$；
求出某一个数的值。

输入格式

第一行包含两个整数 $N$、$M$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $N$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i $ 项的初始值。

接下来 $M$ 行每行包含 $2$ 或 $4$个整数，表示一个操作，具体如下：

操作 $1$：格式：1 x y k 含义：将区间 $[x,y]$ 内每个数加上 $k$；

操作 $2$：格式：2 x 含义：输出第 $x$ 个数的值。

输出格式

输出包含若干行整数，即为所有操作 $2$ 的结果。

样例 #1

样例输入 #1

样例输出 #1

1
2

6
10

提示

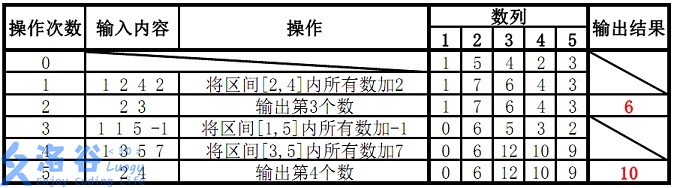
样例 1 解释：

故输出结果为 6、10。

数据规模与约定

对于 $30\%$ 的数据：$N\le8$，$M\le10$；

对于 $70\%$ 的数据：$N\le 10000$，$M\le10000$；

对于 $100\%$ 的数据：$1 \leq N, M\le 500000$，$1 \leq x, y \leq n$，保证任意时刻序列中任意元素的绝对值都不大于 $2^{30}$。

//这个就没什么间接直接了，这样就好了
#include<iostream>
using namespace std;
int n,m;
int tree[10000000];
int lowbit(int x)
{
	return x&-x;
}
void add(int x,int y)
{
	for(int i=x;i<=n;i+=lowbit(i))
	{
		tree[i]+=y;
	}	
}
int sum(int x)
{
	int ans=0;
	for(int i=x;i>0;i-=lowbit(i))
	{
		ans+=tree[i];
	}
	return ans;	
}
int a[10000000];
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
	
		cin>>a[i];
		add(i,a[i]-a[i-1]);
        //差分操作
	}
	while(m--)
	{
		int opt;
		cin>>opt;
		if(opt==1)
		{
			int x,y,k;
			cin>>x>>y>>k;
		add(x,k);
		add(y+1,-k);
		}
		else
		{
			int x;
			cin>>x;
		cout<<sum(x)<<'\n';
		}	
	}
}

逆序对

题目描述

猫猫 TOM 和小老鼠 JERRY 最近又较量上了，但是毕竟都是成年人，他们已经不喜欢再玩那种你追我赶的游戏，现在他们喜欢玩统计。

最近，TOM 老猫查阅到一个人类称之为“逆序对”的东西，这东西是这样定义的：对于给定的一段正整数序列，逆序对就是序列中 $a_i>a_j$ 且 $i<j$ 的有序对。知道这概念后，他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。注意序列中可能有重复数字。

Update:数据已加强。

输入格式

第一行，一个数 $n$，表示序列中有 $n$个数。

第二行 $n$ 个数，表示给定的序列。序列中每个数字不超过 $10^9$。

输出格式

输出序列中逆序对的数目。

样例 #1

样例输入 #1

1 2	6 5 4 2 6 3 1

样例输出 #1

提示

对于 $25\%$ 的数据，$n \leq 2500$

对于 $50\%$ 的数据，$n \leq 4 \times 10^4$。

对于所有数据，$n \leq 5 \times 10^5$

请使用较快的输入输出

应该不会 $O(n^2)$ 过 50 万吧 by chen_zhe

归并排序并且计算逆序对，详见分治与倍增

// P1908 逆序对
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define frep(i, a, n) for (int i = a; i >= n; i--)
const int N = 1e6;
int n, a[N],t[N];
ll ans;
void merge_sort(int a[],int l,int r)
{
    if(l==r)
{
    return ;
}
int mid=l+r>>1;
merge_sort(a,l,mid),merge_sort(a,mid+1,r);
for(int i=l,j=l,k=mid+1;i<=r;i++)
{
    if(j==mid+1)
    {
        t[i]=a[k++];
    }
    else if(k==r+1)
    {
        t[i]=a[j++];
        ans+=k-mid-1;
    }
    else if(a[j]<=a[k])
    {
        t[i]=a[j++];
         ans+=k-mid-1;
    }
    else
    {
        t[i]=a[k++];
    }
}
for (int i = l; i <= r; i++)
{
    a[i] = t[i];
}
}
int main()
{
    cin>>n;
    rep(i,1,n)
    {
        cin>>a[i];
    }
    merge_sort(a,1,n);
    cout<<ans;
    return 0;
}

是时候来发树状数组求解逆序对了。

#include<bits/stdc++.h>
using namespace std;
const int N=500010;
int tree[N],ranks[N],n;
long long ans; 
struct point
{
    int num,val;
}a[500010];
bool cmp(point q,point w)
{
    if(q.val==w.val)
        return q.num<w.num;
    return q.val<w.val;
}
void insert(int p,int d)
{
    for(;p<=n;p+=p&-p)
        tree[p]+=d; 
}
int query(int p)
{
    int sum=0;
    for(;p;p-=p&-p)
        sum+=tree[p];
    return sum;
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
     cin>>a[i].val;
    a[i].num=i;
    }
    sort(a+1,a+1+n,cmp);
    for(int i=1;i<=n;i++)
        ranks[a[i].num]=i;
    for(int i=1;i<=n;i++)
    {
        insert(ranks[i],1);
        ans+=i-query(ranks[i]);
    }
   cout<<ans;
    return 0;
}

[GZOI2017] 配对统计

题目背景

GZOI2017 D1T3

题目描述

给定 $n$ 个数 $a_1,\cdots,a_n$。

给出若干询问，每次询问区间 $[l,r]$ 中含有多少组好的配对。

即，取 $x,y$（$l\le x,y\le r$ 且 $x\not=y$），问有多少组 $(x,y)$ 是好的配对。

输入格式

第一行两个正整数 $n,m$。

第二行 $n$ 个数 $a_1,\cdots,a_n$。

接下来 $m$ 行，每行给出两个数 $l,r$。

输出格式

$Ans_i$ 表示第 $i$ 次询问的答案，输出 $\sum_{i=1}^m\limits Ans_i\times i$ 即可。

样例 #1

样例输入 #1

样例输出 #1

提示

【样例解释】

第一次询问好的配对有：$(1,2)(2,1)$；

第二次询问好的配对有：$(1,2)(2,1),(1,3)(3,1)$；

答案 $=2\times 1+4\times 2=10$。

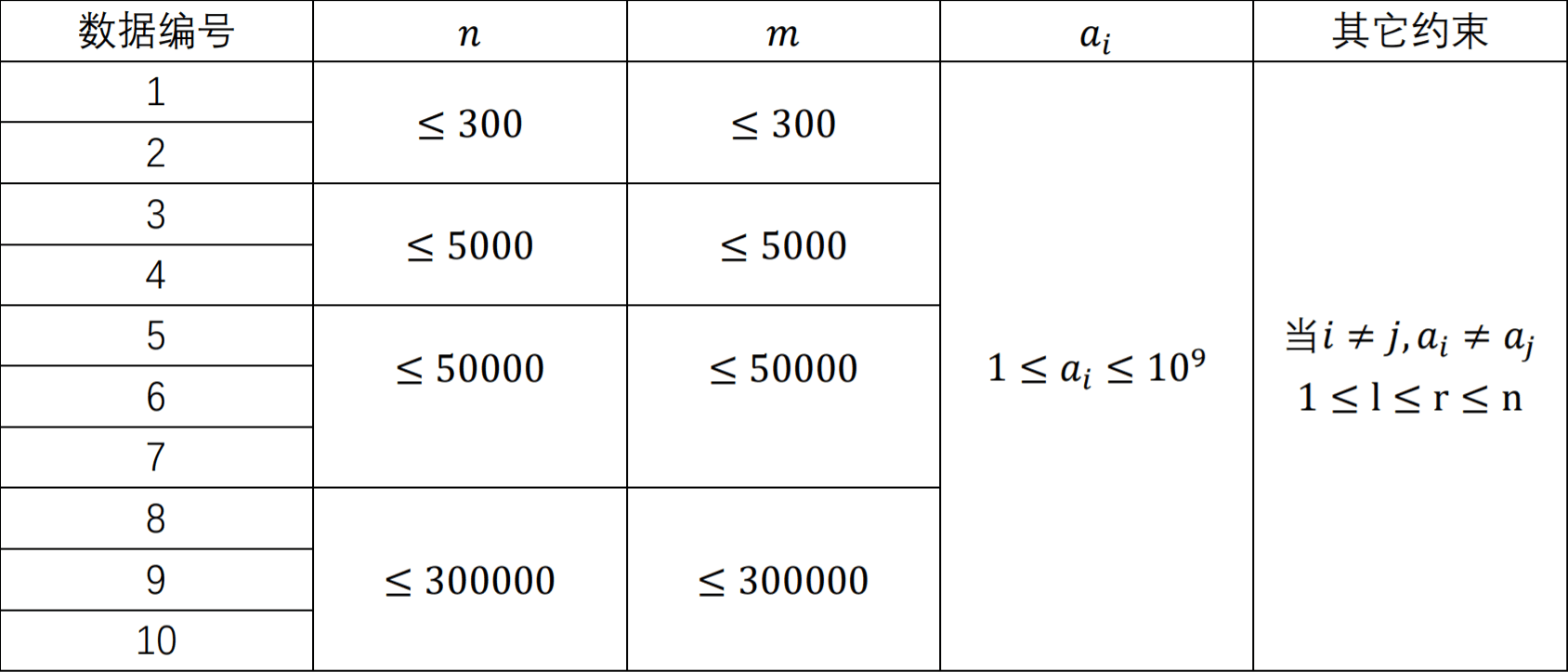
【数据约束】

找到两旁最近好对下标加入,树状数组加入一段减去一端的操作学会了

#include<bits/stdc++.h>
using ll=long long;
using namespace std;
int lowbit(int x)
{	
    return x & (-x);
}
int n,m;
ll tree[300001];
void add(int pos)
{	//单点修改（每次只用加1） 
	while(pos<=n)	
		tree[pos]++,pos+=lowbit(pos);
}
int Query(int num)
{
	ll sum=0;
	while(num>0)
		sum+=tree[num],num-=lowbit(num);
	return sum;
}
//以上为树状数组的单点修改区间查询 
struct Num{	
	ll num;	int pos;	
}a[300001];
//原数组 
bool cmp(Num a1,Num a2)
{
    return a1.num<a2.num;
}	
//原数组进行结构体排序 
struct Pair
{
	int l,r;			
}pairr[600002];
//好对 
int paircnt=0;		
//记录好对个数 
void add_pair(Num a1,Num a2)
{
	int l=min(a1.pos,a2.pos) , r=max(a1.pos,a2.pos);
	//为了方便查询，统一把好对中出现位置较小的那个放在前面 
	pairr[++paircnt].l=l;
	pairr[paircnt].r=r;
	return ;
}
bool cmpPair(Pair a1,Pair a2)
{		//对所有的好对按右端点从小到大排序 
	if(a1.r!=a2.r)	
        return a1.r<a2.r;
	else 
        return a1.l<a2.l;
}
struct Questions{
	int l,r,pos;	
}question[300001];
	//询问 
bool cmpQestions(Questions a1,Questions a2)
{	//对所有的询问按右端点从小到大排序 
	if(a1.r!=a2.r)	
        return a1.r<a2.r;
	else 
        return a1.l<a2.l;
}
int main(){
	cin>>n>>m;
    	if(n==1)
        {
            puts("0");
            return 0;
        }
    //特判
	for(int i=1 ; i<=n ; i++)
    {
		cin>>a[i].num;
		a[i].pos=i;			
        //记录下该数在原先序列里的位置，排完序后方便添加配对 
	}
	sort(a+1,a+1+n,cmp);	
    //排序 
	add_pair(a[1],a[2]);	//首位特殊处理
	add_pair(a[n],a[n-1]);	//末尾特殊处理
    //下面这个for循环用来记录所有点对
	for(int i=2 ; i<n ; i++)
    {
		int ldif = a[i].num-a[i-1].num ;
         int rdif = a[i+1].num-a[i].num;	
        //左边的差 和 右边的差 
		if(ldif<rdif)		
            add_pair(a[i],a[i-1]);		
        //左边差更小，只有左边的一对 
		else if(ldif==rdif)	
            add_pair(a[i],a[i-1]),add_pair(a[i],a[i+1]);
														
        //两边差更小，有两对 
		else				
            add_pair(a[i],a[i+1]);		
        //右边差更小，只有右边的一对 
	}
	sort(pairr+1 , pairr+1+paircnt , cmpPair);	
    //对所有的好对按右端点从小到大排序
	for(int i=1;i<=m;i++)
    {
		cin>>question[i].l>>question[i].r;
		question[i].pos=i;
	}
	sort(question+1 , question+1+m , cmpQestions);
    //对所有的询问按右端点从小到大排序
	ll ans=0;		
    //ans为最终答案
	for(int i=1,j=1 ; i<=m ; i++)
    {	
        //i为当前询问，j为当前待入树状数组的好对 
		while(pairr[j].r<=question[i].r && j<=paircnt)
        {
			add(pairr[j].l);		
            //如果当前好对的右端点在当前询问的右端点内，就加入树状数组 
			j++;
		}
		ans+=1ll * question[i].pos * (j-1- Query(question[i].l-1) );	//计算答案 
	}
	cout<<ans;	
    //输出 
}

[NOIP2013 提高组] 火柴排队

题目背景

NOIP2013 提高组 D1T2

题目描述

涵涵有两盒火柴，每盒装有 $n$ 根火柴，每根火柴都有一个高度。现在将每盒中的火柴各自排成一列，同一列火柴的高度互不相同，两列火柴之间的距离定义为：$ (a_i-b_i)^2$。

其中 $a_i$ 表示第一列火柴中第 $i$ 个火柴的高度，$b_i$ 表示第二列火柴中第 $i$ 个火柴的高度。

每列火柴中相邻两根火柴的位置都可以交换，请你通过交换使得两列火柴之间的距离最小。请问得到这个最小的距离，最少需要交换多少次？如果这个数字太大，请输出这个最小交换次数对 $10^8-3$ 取模的结果。

输入格式

共三行，第一行包含一个整数 $n$，表示每盒中火柴的数目。

第二行有 $n$ 个整数，每两个整数之间用一个空格隔开，表示第一列火柴的高度。

第三行有 $n$ 个整数，每两个整数之间用一个空格隔开，表示第二列火柴的高度。

输出格式

一个整数，表示最少交换次数对 $10^8-3$ 取模的结果。

样例 #1

样例输入 #1

1
2
3

4
2 3 1 4
3 2 1 4

样例输出 #1

样例 #2

样例输入 #2

1
2
3

4
1 3 4 2
1 7 2 4

样例输出 #2

提示

输入输出样例说明一

最小距离是 $ 0$，最少需要交换 $1$ 次，比如：交换第 $1 $ 列的前 $ 2$ 根火柴或者交换第 $2$ 列的前 $2 $ 根火柴。

输入输出样例说明二

最小距离是 $10$，最少需要交换 $2$ 次，比如：交换第 $1$ 列的中间 $2$ 根火柴的位置，再交换第 $2$ 列中后 $2$ 根火柴的位置。

数据范围

对于 $10\%$ 的数据， $1 \leq n \leq 10$；

对于 $30\%$ 的数据，$1 \leq n \leq 100$；

对于 $60\%$ 的数据，$1 \leq n \leq 10^3$；

对于 $100\%$ 的数据，$1 \leq n \leq 10^5$，$0 \leq$ 火柴高度 $< 2^{31}$。

详见分治与倍增

// P1966 [NOIP2013 提高组] 火柴排队
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define frep(i, a, n) for (int i = a; i >= n; i--)
const int N = 1e6;
int n;
struct huocai
{
    int hh, ll;

} a[1000005], b[1000005];

bool cmp(huocai X, huocai Y)
{
    return X.hh < Y.hh;
    // 一个小小的结构体排序
}
int x[N];
int p[N];
ll ans;
const ll mod=1e8-3;
void merge_sort(int a[], int l, int r)
{
    if (l == r)
    {
        return;
    }
    int mid = l + r >> 1;
    merge_sort(a, l, mid), merge_sort(a, mid + 1, r);
    for (int i = l, j = l, k = mid + 1; i <= r; i++)
    {
        if (j == mid + 1)
        {
            p[i] = a[k++];
        }
        else if (k == r + 1)
        {
            p[i] = a[j++];
            ans += k - mid - 1;
        }
        else if (a[j] <= a[k])
        {
            p[i] = a[j++];
            ans += k - mid - 1;
        }
        else
        {
            p[i] = a[k++];
        }
    }
    for (int i = l; i <= r; i++)
    {
        a[i] = p[i];
    }
}

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i].hh;
        a[i].ll = i;
    }
    sort(a + 1, a + 1 + n, cmp);

    for (int i = 1; i <= n; i++)
    {
        cin >> b[i].hh;
        b[i].ll = i;
    }
    sort(b + 1, b + 1 + n, cmp);

    // 两个排序
    for (int i = 1; i <= n; i++)
    {
        x[b[i].ll] = a[i].ll;
        // 一个离散化的过程，如果a和b的排序手法一致，那么会出现一个非常好的现象，就是说这是一个从，1开始到n的一个数列，如果有一个不一样，就会出现逆序对，至于
        // 如果出现逆序对，那么就需要进行归并操作了
        // 接下来，请凯斯你的归并操作，
    }
    merge_sort(x,1,n);

    cout << ans%mod;
    return 0;
}

[SHOI2009] 会场预约

题目背景

形式化描述

你需要维护一个在数轴上的线段的集合 $S$，支持两种操作：

A l r 表示将 $S$ 中所有与线段 $[l,r]$ 相交的线段删去，并将 $[l,r]$ 加入 $S$ 中。

B 查询 $S$ 中的元素数量。

对于 A 操作，每次还需输出删掉的元素个数。

题目描述

PP 大厦有一间空的礼堂，可以为企业或者单位提供会议场地。

这些会议中的大多数都需要连续几天的时间（个别的可能只需要一天），不过场地只有一个，所以不同的会议的时间申请不能够冲突。也就是说，前一个会议的结束日期必须在后一个会议的开始日期之前。所以，如果要接受一个新的场地预约申请，就必须拒绝掉与这个申请相冲突的预约。

一般来说，如果 PP 大厦方面事先已经接受了一个会场预约（例如从 $10$ 日到 $15$ 日），就不会再接受与之相冲突的预约（例如从 $12$ 日到 $17$ 日）。

不过，有时出于经济利益，PP 大厦方面有时会为了接受一个新的会场预约，而拒绝掉一个甚至几个之前预订的预约。于是，礼堂管理员 QQ 的笔记本上经常记录着这样的信息：（本题中为方便起见，所有的日期都用一个整数表示）例如，如果一个为期 $10$ 天的会议从 $90$ 日开始到 $99$ 日，那么下一个会议最早只能在 $100$ 日开始。（此处前后矛盾，若无法理解请参考形式化描述。）

最近，这个业务的工作量与日俱增，礼堂的管理员 QQ 希望参加 SHTSC 的你替他设计一套计算机系统，方便他的工作。这个系统应当能执行下面两个操作：

A 操作：有一个新的预约是从 $start$ 日到 $end$ 日，并且拒绝掉所有与它相冲突的预约。执行这个操作的时候，你的系统应当返回为了这个新预约而拒绝掉的预约个数，以方便 QQ 与自己的记录相校对。

B 操作：请你的系统返回当前的仍然有效的预约的总数。

输入格式

第一行一个正整数 $n$，表示操作个数。
接下来 $n$ 行，每行表示一个操作，都是上面两种中的一个。

输出格式

输出 $n$ 行，每行一个整数，表示对应操作的答案。

样例 #1

样例输入 #1

样例输出 #1

提示

【数据范围】
对于 $100\%$ 的数据，$1\le n \le 2\times 10^5$，$1\le l \le r \le 10^5$。

//STL赛高
#include<bits/stdc++.h>
using namespace std;
struct Plan
{
	int l,r;
	bool operator <(const Plan &rhs)const
    {
		return r<rhs.l;
	}
};
int T;
set<Plan> s;
int main()
{
	cin>>T;
	while(T--)
    {
		char c; 
        cin>>c; //空格可以防止读入无效字符
		if(c=='A')
        {
			int l,r,cnt=0; 
            cin>>l>>r;
			Plan tmp=(Plan){l,r};
			set<Plan>::iterator it=s.find(tmp);
			while(it!=s.end())
            {
				++cnt; s.erase(it);
				it=s.find(tmp);
			}
			s.insert(tmp);
			cout<<cnt<<'\n';
		}
		else
        {
			cout<<s.size()<<'\n';
		}
	}

}

树状数组才是要掌握的（）

#include<bits/stdc++.h>
using namespace std;
const int N=100001;
int tree[N],eend[N];
void add(int x,int c)
{
    for(;x<N;x+=x&-x)tree[x]+=c;
}//数组数组加
int ask(int x)
{
    int sum=0;
    for(;x;x&=x-1)sum+=tree[x];
    return sum;
}//数组数组求和
//上面为树状数组模板
int main()
{
    int n;int ans=0;
    cin>>n;
   while(n--)
   {
        scanf("\n");
       //不这样会wa
        if(getchar()=='A')
        {
            int del=0,st,ed;
            cin>>st>>ed;
            for(int p;p=ask(ed);)
                //不断往后查询
            {
                int l=0,r=ed;
                for(;l<r;)
                {
                    int m=(l+r)>>1;
                    if(ask(m)+1<=p)
                        l=m+1;
                    else 
                        r=m;
                }//二分找到最后可能交叉的区间
                if(eend[l]>=st)
                    add(l,-1),del++,ans--;
                else break;
            }
            add(st,1);
            eend[st]=ed;ans++;
            cout<<del<<'\n';
        }
        else cout<<ans<<'\n';
    }
    return 0;
}

世间温柔，不过是芳春柳摇染花香，槐序蝉鸣入深巷，白茂叶落醉故乡。

序号	操作	\(i\)	数据库	输出
1	`ADD(3)`	\(0\)	\(3\)	/
2	`GET`	\(1\)	\(3\)	\(3\)
3	`ADD(1)`	\(1\)	\(1,3\)	/
4	`GET`	\(2\)	\(1,3\)	\(3\)
5	`ADD(-4)`	\(2\)	\(-4,1,3\)	/
6	`ADD(2)`	\(2\)	\(-4,1,2,3\)	/
7	`ADD(8)`	\(2\)	\(-4,1,2,3,8\)	/
8	`ADD(-1000)`	\(2\)	\(-1000,-4,1,2,3,8\)	/
9	`GET`	\(3\)	\(-1000,-4,1,2,3,8\)	\(1\)
10	`GET`	\(4\)	\(-1000,-4,1,2,3,8\)	\(2\)
11	`ADD(2)`	\(4\)	\(-1000,-4,1,2,2,3,8\)	/

测试点编号	\(n\) 的规模	\(k\) 的规模	备注
\(1\)	\(n=3\)	\(k=2\)
\(2\)	\(n=5\)	\(k=2\)
\(3\)	\(n=16\)	\(k=2\)	所有 \(w_i\) 均相等
\(4\)	\(n=1\,000\)	\(k=2\)	\(w_i\) 在取值范围内均匀随机
\(5\)	\(n=1\,000\)	\(k=2\)
\(6\)	\(n=100\,000\)	\(k=2\)
\(7\)	\(n=100\,000\)	\(k=2\)	所有 \(w_i\) 均相等
\(8\)	\(n=100\,000\)	\(k=2\)
\(9\)	\(n=7\)	\(k=3\)
\(10\)	\(n=16\)	\(k=3\)	所有 \(w_i\) 均相等
\(11\)	\(n=1\,001\)	\(k=3\)	所有 \(w_i\) 均相等
\(12\)	\(n=99\,999\)	\(k=4\)	所有 \(w_i\) 均相等
\(13\)	\(n=100\,000\)	\(k=4\)
\(14\)	\(n=100\,000\)	\(k=4\)
\(15\)	\(n=1\,000\)	\(k=5\)
\(16\)	\(n=100\,000\)	\(k=7\)	\(w_i\) 在取值范围内均匀随机
\(17\)	\(n=100\,000\)	\(k=7\)
\(18\)	\(n=100\,000\)	\(k=8\)	\(w_i\) 在取值范围内均匀随机
\(19\)	\(n=100\,000\)	\(k=9\)
\(20\)	\(n=100\,000\)	\(k=9\)