分治与倍增

分治是解编程题常用的一种思想，而大多数分治思想都是用递归来实现的。

分治（divide and conquer）的全称称为“分而治之”，分治即是将大问题划分为若干个规模较小、可以直接解决的子问题，然后解决这些子问题，最后将这些子问题的解合并起来，即是原问题的解。

递归就是这个函数反复调用自身，然后将问题一步步地缩小，直到这个问题已经缩小到可以直接解决的程度，然后再一步一步地返回，最终解决原问题。

递归的逻辑中有两个重要的概念： 1.递归边界。递归边界是分解的尽头。 2.递归式。递归式是将问题规模一步步缩小的手段。

常见的递归

1
2
3
4
5
6
7
8
9
10
11
12
int gcd(int a,intb)
{
    if(b==0)return a;
    else return gcd(b,a%b);
}

int Fibonacci(int n)
{
     if(n==0||n==1)return 1;
     else return Fibonacci(n-1)+Fibonacci(n-2);
}

步骤

  • 分(Divide)：递归解决较小的问题(到终止层或者可以解决的时候停下)

  • 治(Conquer)：递归求解，如果问题够小直接求解。

  • 合并(Combine)：将子问题的解构建父类问题

    适应：

    1 . 原问题规模通常比较大，不易直接解决，但问题缩小到一定程度就能较容易的解决。

    2 . 问题可以分解为若干规模较小、求解方式相同(似)的子问题。且子问题之间求解是独立的互不影响。

    3 . 合并问题分解的子问题可以得到问题的解。

倍增则是一种基础算法，但它能够使得线性的处理转化为对数级的处理，大大地优化时间复杂度，在很多算法中都有应用，其中最常见的就是ST表以及LCA（树上最近公共祖先）了。

例子：

31个1可以，下面5个数也可以

只需要为 1,2,4,8,16 的数字，就能表示 [1,31] 内的所有数字

跳跃很多步数，每一步拿胡萝卜，这些步数可以拆分为：跳 1,2,4,8,16…次

image-20240225083025907

倍增应用：ST表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
using ll=long long;
int st[N][20];
int lg[N];
int n,m;
int main()
{
    ios::sync_with_stdio(0);
 	cin.tie(0);
 	cout.tie(0);
    cin>>n>>m;
    lg[1]=0;
    for(int i=2;i<=n;i++)
    {
        lg[i]=lg[i>>1]+1;
    }
    for(int i=1;i<=n;i++)
    {
        cin>>st[i][0];
    }
    for(int j=1;j<=lg[n];j++)
    {
        for(int i=1;i+(1<<j)-1<=n;i++)
        {
            st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]);
		}
	}
    int l,r;
    while(m--)
    {
        cin>>l>>r;
        int t=lg[r-l+1];
        cout<<max(st[l][t],st[r-(1<<t)+1][t])<<'\n';
    }  
}

LCA模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include<bits/stdc++.h>
using namespace std;
const int N=6e5;
int n,m,s,t,tot=0,f[N][20],d[N],ver[2*N],Next[2*N],head[N];
queue<int> q;
void add(int x,int y)
{
    ver[++tot]=y,Next[tot]=head[x],head[x]=tot;
}
void bfs()
{
    q.push(s);
    d[s]=1;//将根节点入队并标记
    while(q.size())
    {
        int x=q.front();q.pop();//取出队头
        for(int i=head[x];i;i=Next[i])
        {
            int y=ver[i];
            if(d[y])
                continue;
            d[y]=d[x]+1;
            f[y][0]=x;//初始化，因为y的父亲节点就是x
            for(int j=1;j<=t;j++)
                f[y][j]=f[f[y][j-1]][j-1];//递推f数组
            q.push(y);
        }
    }
}
int lca(int x,int y)
{
    if(d[x]>d[y])
        swap(x,y);
    for(int i=t;i>=0;i--)
        if(d[f[y][i]]>=d[x])
            y=f[y][i];//尝试上移y
    if(x==y)
        return x;//若相同说明找到了LCA
    for(int i=t;i>=0;i--)
        if(f[x][i]!=f[y][i])
        {
            x=f[x][i],y=f[y][i];
        }//尝试上移x、y并保持它们不相遇
    return f[x][0];//当前节点的父节点即为LCA
}
int main()
{
    cin>>n>>m>>s;
    t=log2(n)+1;
    for(int i=1;i<n;i++)
    {
        int x,y;
        cin>>x>>y;
        add(x,y),add(y,x);
    }
    bfs();
    while(m--)
    {
        int a,b;
        cin>>a>>b;
 cout<<lca(a,b)<<'\n';
    }
    return 0;
}

【模板】排序

题目描述

将读入的 \(N\) 个数从小到大排序后输出。

输入格式

第一行为一个正整数 \(N\)。

第二行包含 \(N\) 个空格隔开的正整数 \(a_i\)，为你需要进行排序的数。

输出格式

将给定的 \(N\) 个数从小到大输出，数之间空格隔开，行末换行且无空格。

样例 #1

样例输入 #1

1
2
5
4 2 4 5 1

样例输出 #1

1
1 2 4 4 5

提示

对于 \(20\%\) 的数据，有 \(1 \leq N \leq 10^3\)；

对于 \(100\%\) 的数据，有 \(1 \leq N \leq 10^5\)，\(1 \le a_i \le 10^9\)。

这个就是堆罢，堆发的一种排序写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include<bits/stdc++.h>
using namespace std;
const int N=1e7;
int w[N];
int tot;
#define rep(i,a,n) for(int i=a;i<=n;i++)
//一个是数组，一个是最后一个节点所在位置
//1.top操作
int top()
{
    return w[1];
    //返回堆顶也就是最大值
}
void modify(int x)
{
if(x==1||w[x]<w[x/2])
{
    return ;
    //就是你已经到达根顶了，或者你已经小于你的父节点了
    //这样就行了实际上
}
swap(w[x],w[x/2]);
//这也正是没有达到上述情况，那么你就要交换
modify(x/2);
//交换完继续处理上一个节点
//递归处理
}
void push(int x)
{
    w[++tot]=x;//加入元素直接在尾部进行加入
    modify(tot);//自底向上修复
}
void repair(int x)
{
if(x*2>tot)
{
    return ;
    //已经到达叶子节点，和上个modify操作一样
}
int tar=2*x;
if(x*2+1<=tot)
{
    tar=w[x*2]>w[x*2+1]?x*2:x*2+1;
}
if(w[x]<w[tar])
{
    swap(w[x],w[tar]);
    repair(tar);
}
}
void pop()
{
    swap(w[1],w[tot--]);
    //这一步有两个操作，第一个是交换头尾，第二个是删除尾部
   //接下来我们要修复头部
   repair(1); 
}
int main()
{
int n;
cin>>n;
rep(i,1,n)
{
    int x;
    cin>>x;
    push(-x);
}
rep(i,1,n)
{
    cout<<-top()<<' ';
    pop();
}
return 0;
}

逆序对

题目描述

猫猫 TOM 和小老鼠 JERRY 最近又较量上了，但是毕竟都是成年人，他们已经不喜欢再玩那种你追我赶的游戏，现在他们喜欢玩统计。

最近，TOM 老猫查阅到一个人类称之为“逆序对”的东西，这东西是这样定义的：对于给定的一段正整数序列，逆序对就是序列中 \(a_i>a_j\) 且 \(i<j\) 的有序对。知道这概念后，他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。注意序列中可能有重复数字。

Update:数据已加强。

输入格式

第一行，一个数 \(n\)，表示序列中有 \(n\)个数。

第二行 \(n\) 个数，表示给定的序列。序列中每个数字不超过 \(10^9\)。

输出格式

输出序列中逆序对的数目。

样例 #1

样例输入 #1

1
2
6
5 4 2 6 3 1

样例输出 #1

1
11

提示

对于 \(25\%\) 的数据，\(n \leq 2500\)

对于 \(50\%\) 的数据，\(n \leq 4 \times 10^4\)。

对于所有数据，\(n \leq 5 \times 10^5\)

请使用较快的输入输出

应该不会 \(O(n^2)\) 过 50 万吧 by chen_zhe

归并排序模板题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
// P1908 逆序对
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define frep(i, a, n) for (int i = a; i >= n; i--)
const int N = 1e6;
int n, a[N],t[N];
ll ans;
void merge_sort(int a[],int l,int r)
{
    if(l==r)
{
    return ;
}
    //将一个序列进行二分，直到分解成n个元素（l == r）
int mid=l+r>>1;
merge_sort(a,l,mid),merge_sort(a,mid+1,r);
for(int i=l,j=l,k=mid+1;i<=r;i++)
{
    if(j==mid+1)
    {
        t[i]=a[k++];
    }
    else if(k==r+1)
    {
        t[i]=a[j++];
        ans+=k-mid-1;
    }
    else if(a[j]<=a[k])//如果前面的元素比后面大(l ~ mid中的元素 > mid + 1 ~ r中的元素)(逆序对出现!!!) 
    {
        t[i]=a[j++];
         ans+=k-mid-1;
    }
    else
    {
        t[i]=a[k++];
    }
}
    //将已有序的子序列合并（二分到最后的时候，一个元素一定是有序的），得到完全有序的序列
    
for (int i = l; i <= r; i++)
{
    a[i] = t[i];
}
    //将已有序的b数组赋值到a数组（原数组）里
}
int main()
{
    cin>>n;
    rep(i,1,n)
    {
        cin>>a[i];
    }
    merge_sort(a,1,n);
    cout<<ans;
    return 0;
}

[NOIP2013 提高组] 火柴排队

题目背景

NOIP2013 提高组 D1T2

题目描述

涵涵有两盒火柴，每盒装有 \(n\) 根火柴，每根火柴都有一个高度。 现在将每盒中的火柴各自排成一列， 同一列火柴的高度互不相同， 两列火柴之间的距离定义为：$ (a_i-b_i)^2$。

其中 \(a_i\) 表示第一列火柴中第 \(i\) 个火柴的高度，\(b_i\) 表示第二列火柴中第 \(i\) 个火柴的高度。

每列火柴中相邻两根火柴的位置都可以交换，请你通过交换使得两列火柴之间的距离最小。请问得到这个最小的距离，最少需要交换多少次？如果这个数字太大，请输出这个最小交换次数对 \(10^8-3\) 取模的结果。

输入格式

共三行，第一行包含一个整数 \(n\)，表示每盒中火柴的数目。

第二行有 \(n\) 个整数，每两个整数之间用一个空格隔开，表示第一列火柴的高度。

第三行有 \(n\) 个整数，每两个整数之间用一个空格隔开，表示第二列火柴的高度。

输出格式

一个整数，表示最少交换次数对 \(10^8-3\) 取模的结果。

样例 #1

样例输入 #1

1
2
3
4
2 3 1 4
3 2 1 4

样例输出 #1

1
1

样例 #2

样例输入 #2

1
2
3
4
1 3 4 2
1 7 2 4

样例输出 #2

1
2

提示

输入输出样例说明一

最小距离是 $ 0$，最少需要交换 \(1\) 次，比如：交换第 $1 $ 列的前 $ 2$ 根火柴或者交换第 \(2\) 列的前 $2 $ 根火柴。

输入输出样例说明二

最小距离是 \(10\)，最少需要交换 \(2\) 次，比如：交换第 \(1\) 列的中间 \(2\) 根火柴的位置，再交换第 \(2\) 列中后 \(2\) 根火柴的位置。

数据范围

对于 \(10\%\) 的数据， \(1 \leq n \leq 10\)；

对于 \(30\%\) 的数据，\(1 \leq n \leq 100\)；

对于 \(60\%\) 的数据，\(1 \leq n \leq 10^3\)；

对于 \(100\%\) 的数据，\(1 \leq n \leq 10^5\)，\(0 \leq\) 火柴高度 \(< 2^{31}\)。

归并排序

本题破解之法：顺序x顺序>=乱序x乱序；

1
2
Σ(ai^2-2*ai*bi+bi^2)=Σ(ai^2+bi^2)-Σ(2*ai*bi)
     Σ(2*ai*bi)=2*Σ(ai*bi)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
// P1966 [NOIP2013 提高组] 火柴排队
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define frep(i, a, n) for (int i = a; i >= n; i--)
const int N = 1e6;
int n;
struct huocai
{
    int hh, ll;

} a[1000005], b[1000005];

bool cmp(huocai X, huocai Y)
{
    return X.hh < Y.hh;
    // 一个小小的结构体排序
}
int x[N];
int p[N];
ll ans;
const ll mod=1e8-3;
void merge_sort(int a[], int l, int r)
{
    if (l == r)
    {
        return;
    }
    int mid = l + r >> 1;
    merge_sort(a, l, mid), merge_sort(a, mid + 1, r);
    for (int i = l, j = l, k = mid + 1; i <= r; i++)
    {
        if (j == mid + 1)
        {
            p[i] = a[k++];
        }
        else if (k == r + 1)
        {
            p[i] = a[j++];
            ans += k - mid - 1;
        }
        else if (a[j] <= a[k])
        {
            p[i] = a[j++];
            ans += k - mid - 1;
        }
        else
        {
            p[i] = a[k++];
        }
    }
    for (int i = l; i <= r; i++)
    {
        a[i] = p[i];
    }
}

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i].hh;
        a[i].ll = i;
    }
    sort(a + 1, a + 1 + n, cmp);

    for (int i = 1; i <= n; i++)
    {
        cin >> b[i].hh;
        b[i].ll = i;
    }
    sort(b + 1, b + 1 + n, cmp);

    // 两个排序
    for (int i = 1; i <= n; i++)
    {
        x[b[i].ll] = a[i].ll;
        // 一个离散化的过程，如果a和b的排序手法一致，那么会出现一个非常好的现象，就是说这是一个从，1开始到n的一个数列，如果有一个不一样，就会出现逆序对，至于
        // 如果出现逆序对，那么就需要进行归并操作了
        // 接下来，请凯斯你的归并操作，
    }
    merge_sort(x,1,n);

    cout << ans%mod;
    return 0;
}

【模板】快速幂

题目描述

给你三个整数 \(a,b,p\)，求 \(a^b \bmod p\)。

输入格式

输入只有一行三个整数，分别代表 \(a,b,p\)。

输出格式

输出一行一个字符串 a^b mod p=s，其中 \(a,b,p\) 分别为题目给定的值， \(s\) 为运算结果。

样例 #1

样例输入 #1

1
2 10 9

样例输出 #1

1
2^10 mod 9=7

提示

样例解释

\(2^{10} = 1024\)，\(1024 \bmod 9 = 7\)。

数据规模与约定

对于 \(100\%\) 的数据，保证 \(0\le a,b < 2^{31}\)，\(a+b>0\)，\(2 \leq p \lt 2^{31}\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include<iostream>
using namespace std;
long long b, a, p, k, ans = 1, c;
int main()
{
    cin>>b>>p>>k;
    a = b; c = p;
    while (p > 0)//快速幂
    {
        if (p &1)
            ans = ans * b % k;//如果p为单数，乘到ans里面去，然后取模
        b = b * b % k;//每次运算都取模
        p = p >> 1;    //用位运算除2，可能会快一点
    }
    ans %= k;
    printf("%d^%d mod %d=%d", a, c, k, ans);
}

[NOIP2003 普及组] 麦森数

题目描述

形如 \(2^{P}-1\) 的素数称为麦森数，这时 \(P\) 一定也是个素数。但反过来不一定，即如果 \(P\) 是个素数，\(2^{P}-1\) 不一定也是素数。到 1998 年底，人们已找到了 37 个麦森数。最大的一个是 \(P=3021377\)，它有 909526 位。麦森数有许多重要应用，它与完全数密切相关。

任务：输入 \(P(1000<P<3100000)\)，计算 \(2^{P}-1\) 的位数和最后 \(500\) 位数字（用十进制高精度数表示）

输入格式

文件中只包含一个整数 \(P(1000<P<3100000)\)

输出格式

第一行：十进制高精度数 \(2^{P}-1\) 的位数。

第 \(2\sim 11\) 行：十进制高精度数 \(2^{P}-1\) 的最后 \(500\) 位数字。（每行输出 \(50\) 位，共输出 \(10\) 行，不足 \(500\) 位时高位补 \(0\)）

不必验证 \(2^{P}-1\) 与 \(P\) 是否为素数。

样例 #1

样例输入 #1

1
1279

样例输出 #1

1
2
3
4
5
6
7
8
9
10
11
386
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000104079321946643990819252403273640855
38615262247266704805319112350403608059673360298012
23944173232418484242161395428100779138356624832346
49081399066056773207629241295093892203457731833496
61583550472959420547689811211693677147548478866962
50138443826029173234888531116082853841658502825560
46662248318909188018470682222031405210266984354887
32958028878050869736186900714720710555703168729087

提示

【题目来源】

NOIP 2003 普及组第四题

详见数学基本问题那里（）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include<bits/stdc++.h>
using namespace std;
int P;
long long a[510];
long long POW2(int a)
{
    long long res=1;
    for(int i=1;i<=a;i++)
    {
        res*=2;
    }
    return res;
}
int main()
{
    cin>>P;
    cout<<ceil(P*log10(2))<<'\n'; 
    long long tmp=POW2(32);      
    a[500]=1;
    int t32=P/32;                 
	int t1=P-t32*32;            
    for(int T=1;T<=t32;T++)
    {
        for(int i=500;i>=1;i--)
        {
            a[i]*=tmp;            
        }
        for(int i=500;i>=1;i--)
        {
            a[i-1]+=a[i]/10;
            a[i]%=10;             
        }
    }
    for(int T=1;T<=t1;T++)
    {
        for(int i=500;i>=1;i--)
        {
            a[i]*=2;              
        }
        for(int i=500;i>=1;i--)
        {
            a[i-1]+=a[i]/10;
            a[i]%=10;             
        }
    }
    a[500]--;
    //直接减去即可
    for(int i=1;i<=500;i++)
    {
        cout<<a[i];
        if(i%50==0) cout<<'\n';
    }

}

最大子段和

题目描述

给出一个长度为 \(n\) 的序列 \(a\)，选出其中连续且非空的一段使得这段和最大。

输入格式

第一行是一个整数，表示序列的长度 \(n\)。

第二行有 \(n\) 个整数，第 \(i\) 个整数表示序列的第 \(i\) 个数字 \(a_i\)。

输出格式

输出一行一个整数表示答案。

样例 #1

样例输入 #1

1
2
7
2 -4 3 -1 2 -4 3

样例输出 #1

1
4

提示

样例 1 解释

选取 \([3, 5]\) 子段 \(\{3, -1, 2\}\)，其和为 \(4\)。

数据规模与约定

  • 对于 \(40\%\) 的数据，保证 \(n \leq 2 \times 10^3\)。
  • 对于 \(100\%\) 的数据，保证 \(1 \leq n \leq 2 \times 10^5\)，\(-10^4 \leq a_i \leq 10^4\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <bits/stdc++.h>
using namespace std;
const int N = 1e7;
#define rep(i, a, n) for (int i = a; i <= n; i++)
using ll=long long;
int a;
int main()
{
int n;
cin>>n;
int f=0;
int ans=-999999999;
rep(i,1,n)
{
cin>>a;
f=max(f+a,a);
//如果加上比这个值本身还小，加他干什么呢
ans=max(f,ans);
//维护作用
}
cout<<ans;
}

[USACO07JAN] Balanced Lineup G

题目描述

For the daily milking, Farmer John's N cows (1 ≤ N ≤ 50,000) always line up in the same order. One day Farmer John decides to organize a game of Ultimate Frisbee with some of the cows. To keep things simple, he will take a contiguous range of cows from the milking lineup to play the game. However, for all the cows to have fun they should not differ too much in height.

Farmer John has made a list of Q (1 ≤ Q ≤ 180,000) potential groups of cows and their heights (1 ≤ height ≤ 1,000,000). For each group, he wants your help to determine the difference in height between the shortest and the tallest cow in the group.

每天,农夫 John 的 \(n(1\le n\le 5\times 10^4)\) 头牛总是按同一序列排队。

有一天, John 决定让一些牛们玩一场飞盘比赛。他准备找一群在队列中位置连续的牛来进行比赛。但是为了避免水平悬殊，牛的身高不应该相差太大。John 准备了 \(q(1\le q\le 1.8\times10^5)\) 个可能的牛的选择和所有牛的身高 \(h_i(1\le h_i\le 10^6,1\le i\le n)\)。他想知道每一组里面最高和最低的牛的身高差。

输入格式

Line 1: Two space-separated integers, N and Q.

Lines 2..N+1: Line i+1 contains a single integer that is the height of cow i

Lines N+2..N+Q+1: Two integers A and B (1 ≤ A ≤ B ≤ N), representing the range of cows from A to B inclusive.

第一行两个数 \(n,q\)。

接下来 \(n\) 行，每行一个数 \(h_i\)。

再接下来 \(q\) 行，每行两个整数 \(a\) 和 \(b\)，表示询问第 \(a\) 头牛到第 \(b\) 头牛里的最高和最低的牛的身高差。

输出格式

Lines 1..Q: Each line contains a single integer that is a response to a reply and indicates the difference in height between the tallest and shortest cow in the range.

输出共 \(q\) 行，对于每一组询问，输出每一组中最高和最低的牛的身高差。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
10
6 3
1
7
3
4
2
5
1 5
4 6
2 2

样例输出 #1

1
2
3
6
3
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
//ST表查询最大值和最小值模板
#include<bits/stdc++.h>
using namespace std;
const int N=50010;
int n,q,h[N],log_2[N],rmax[N][18],rmin[N][18];
void init()
{
    for(int i=1;i<=n;i++)
    {
        rmax[i][0]=rmin[i][0]=h[i];
    }
    for(int j=1;(1<<j)<=n;j++)
    {
        for(int i=1;i<=n-(1<<j)+1;i++)
        {
            rmax[i][j]=max(rmax[i][j-1],rmax[i+(1<<j -1)][j-1]);
            rmin[i][j]=max(rmin[i][j-1],rmin[i+(1<<j-1)][j-1]);
        }
    }
}
int query_max(int a,int b)
{
    int x=log_2[b-a+1];
    return max(rmax[a][x],rmax[b-(1<<x)+1][x]);
}
int query_min(int a, int b)
{
    int x = log_2[b - a + 1];
    return min(rmin[a][x], rmin[b - (1 << x) + 1][x]);
}
int main()
{
cin>>n>>q;
for(int i=1;i<=n;i++)
{
    cin>>h[i];
}
for(int i=2;i<=n;i++)
{
    log_2[i]=log_2[i>>1]+1;
}
init();
while(q--)
{
    int a,b;
    cin>>a>>b;
    cout<<query_max(a,b)-query_min(a,b)<<'\n';
}
}

[eJOI2020 Day1] Fountain

题目描述

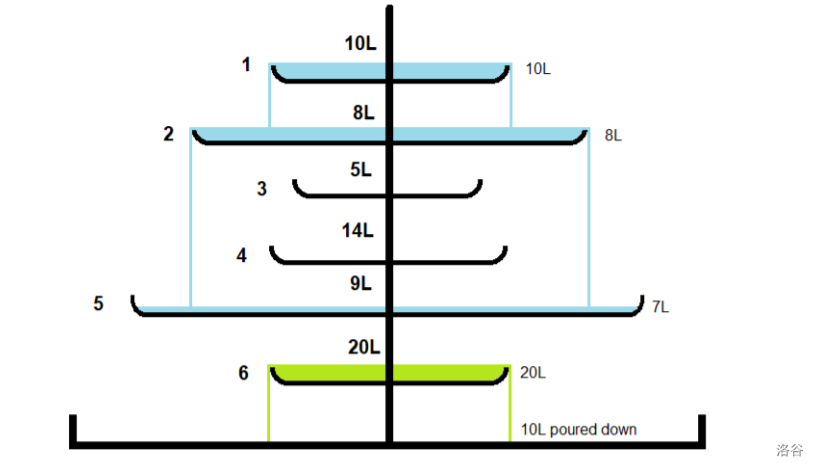
大家都知道喷泉吧？现在有一个喷泉由 \(N\) 个圆盘组成，从上到下以此编号为 \(1 \sim N\)，第 \(i\) 个喷泉的直径为 \(D_i\)，容量为 \(C_i\)，当一个圆盘里的水大于了这个圆盘的容量，那么水就会溢出往下流，直到流入半径大于这个圆盘的圆盘里。如果下面没有满足要求的圆盘，水就会流到喷泉下的水池里。

现在给定 \(Q\) 组询问，每一组询问这么描述：

  • 向第 \(R_i\) 个圆盘里倒入 \(V_i\) 的水，求水最后会流到哪一个圆盘停止。

如果最终流入了水池里，那么输出 \(0\)。

注意，每个询问互不影响。

输入格式

第一行两个整数 \(N,Q\) 代表圆盘数和询问数。
接下来 \(N\) 行每行两个整数 \(D_i,C_i\) 代表一个圆盘。
接下来 \(Q\) 行每行两个整数 \(R_i,V_i\) 代表一个询问。

输出格式

\(Q\) 行每行一个整数代表询问的答案。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
10
11
12
6 5
4 10
6 8
3 5
4 14
10 9
4 20
1 25
6 30
5 8
3 13
2 8

样例输出 #1

1
2
3
4
5
5
0
5
4
2

提示

样例 1 解释

前两个询问的解释如下图所示：

因为每个询问互不影响，对于第三个询问，第 \(5\) 个圆盘里的水不会溢出。

数据规模与约定

本题采用捆绑测试。

  • Subtask 1（30 pts）：\(N \le 1000\)，\(Q \le 2000\)。
  • Subtask 2（30 pts）：\(D_i\) 为严格单调递增序列。
  • Subtask 3（40 pts）：无特殊限制。

对于 \(100\%\) 的数据：

  • \(2 \le N \le 10^5\)。
  • \(1 \le Q \le 2 \times 10^5\)。
  • \(1 \le C_i \le 1000\)。
  • \(1 \le D_i,V_i \le 10^9\)。
  • $ 1R_i N$。

说明

翻译自 eJOI 2020 Day1 A Fountain。

也许会有单调栈+循环的解法（超时）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
//ne[i][j]代表从i开始，往后数2^j个满足能把从i倒下来的水接到的石块的下标。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
int d[N],c[N];
int ne[N][31],sum[N][31];
int st[N],t;
int n,q;
void init(){
    for(int i=1;i<=n;i++)
    {
        sum[i][0]=c[i];
    }
    //一开始
    for(int i=1;i<=23;i++)
    {
        for(int j=1;j<=n;j++)
        {
            ne[j][i]=ne[ne[j][i-1]][i-1];
            sum[j][i]=sum[j][i-1]+sum[ne[j][i-1]][i-1];
        }
    }
    //倍增过程
}

int main(){
    cin>>n>>q;
    for(int i=1;i<=n;i++)
        cin>>d[i]>>c[i];
    for(int i=n;i>=1;i--)
    {
        while(t && d[st[t]]<=d[i])
            t--;
        ne[i][0]=st[t];
        st[++t]=i;
    }
    //单调栈求解第一个大于
    init();
    while(q--){
        int a,b;
        cin>>a>>b;
        for(int i=23;i>=0;i--)
        {
            if(sum[a][i]<b)
            {
                b-=sum[a][i];
                a=ne[a][i];
            }
            //一直跳
        }
        cout<<a<<'\n';
    }

}

集合求和

题目描述

给定一个集合 \(s\)（集合元素数量 \(\le 30\)），求出此集合所有子集元素之和。

输入格式

集合中的元素（元素 \(\le 1000\)）

输出格式

\(s\) 所有子集元素之和。

样例 #1

样例输入 #1

1
2 3

样例输出 #1

1
10

提示

【样例解释】

子集为：\(\varnothing, \{ 2 \}, \{ 3 \}, \{ 2, 3 \}\)，和为 \(2 + 3 + 2 + 3 = 10\)。

【数据范围】

对于 \(100 \%\) 的数据，\(1 \le \lvert s \rvert \le 30\)，\(1 \le s_i \le 1000\)，\(s\) 所有子集元素之和 \(\le {10}^{18}\)。

image-20240224212449701 
1
2
3
4
5
6
7
8
9
10
11
12
#include <bits/stdc++.h>
using namespace std;
int main()
{
    long long ans=0;
    int n=0,i,a;
    while(cin>>a)
    ans+=a,n++; 
    for(i=1;i<n;i++)ans*=2;   
 cout<<ans;

}

平面上的最接近点对

题目描述

给定平面上 \(n\) 个点，找出其中的一对点的距离，使得在这 \(n\) 个点的所有点对中，该距离为所有点对中最小的。

输入格式

第一行一个整数 \(n\)，表示点的个数。

接下来 \(n\) 行，每行两个整数 \(x,y\) ，表示一个点的行坐标和列坐标。

输出格式

仅一行，一个实数，表示最短距离，四舍五入保留 \(4\) 位小数。

样例 #1

样例输入 #1

1
2
3
4
3
1 1
1 2
2 2

样例输出 #1

1
1.0000

提示

数据规模与约定

对于 \(100\%\) 的数据，保证 \(1 \leq n \leq 10^4\)，\(0 \leq x, y \leq 10^9\)。

好像是上个暑假做的，乐了（）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<cstdio>
#include<cmath>
#include<iostream>
using namespace std;
int n, x[10009], y[10009];
double ans = 233333333;
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++) { scanf("%d%d", &x[i], &y[i]); }
    for (int i = 1; i <= n; i++)
    {
        for (int j = i + 1; j <= n; j++)
        {
            if (sqrt((x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j])) < ans) { ans = sqrt((x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j])); }
        }
    }
    printf("%.4lf", ans);
    return 0;
}

地毯填补问题

题目描述

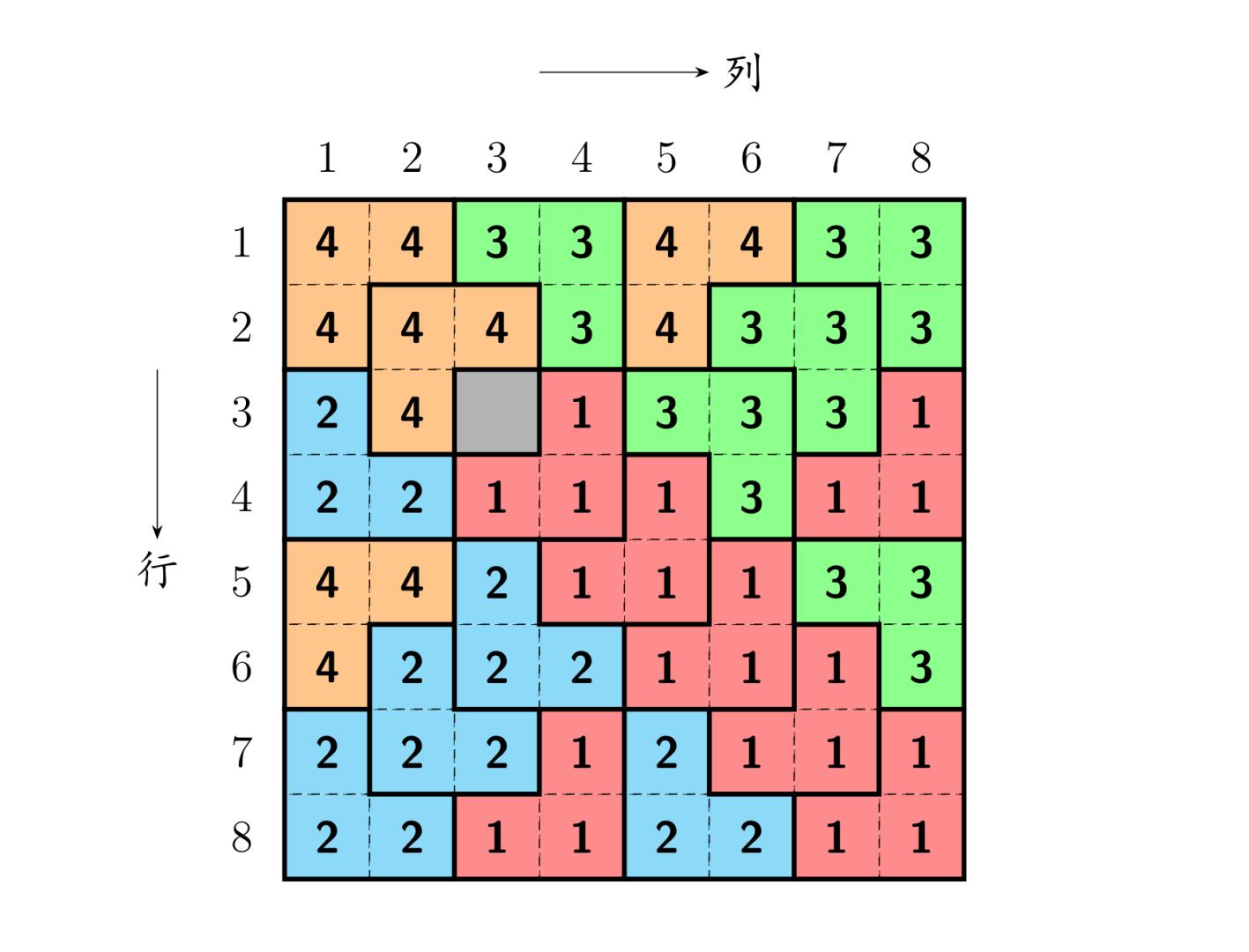
相传在一个古老的阿拉伯国家里，有一座宫殿。宫殿里有个四四方方的格子迷宫，国王选择驸马的方法非常特殊，也非常简单：公主就站在其中一个方格子上，只要谁能用地毯将除公主站立的地方外的所有地方盖上，美丽漂亮聪慧的公主就是他的人了。公主这一个方格不能用地毯盖住，毯子的形状有所规定，只能有四种选择（如图）：

并且每一方格只能用一层地毯，迷宫的大小为 \(2^k\times 2^k\) 的方形。当然，也不能让公主无限制的在那儿等，对吧？由于你使用的是计算机，所以实现时间为 \(1\) 秒。

输入格式

输入文件共 \(2\) 行。

第一行一个整数 \(k\)，即给定被填补迷宫的大小为 \(2^k\times 2^k\)（\(0\lt k\leq 10\)）； 第二行两个整数 \(x,y\)，即给出公主所在方格的坐标（\(x\) 为行坐标，\(y\) 为列坐标），\(x\) 和 \(y\) 之间有一个空格隔开。

输出格式

将迷宫填补完整的方案：每一补（行）为 \(x\ y\ c\)（\(x,y\) 为毯子拐角的行坐标和列坐标，\(c\) 为使用毯子的形状，具体见上面的图 \(1\)，毯子形状分别用 \(1,2,3,4\) 表示，\(x,y,c\) 之间用一个空格隔开）。

样例 #1

样例输入 #1

1
2
3                          
3 3

样例输出 #1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
5 5 1
2 2 4
1 1 4
1 4 3
4 1 2
4 4 1
2 7 3
1 5 4
1 8 3
3 6 3
4 8 1
7 2 2
5 1 4
6 3 2
8 1 2
8 4 1
7 7 1
6 6 1
5 8 3
8 5 2
8 8 1

提示

spj 报错代码解释：

  1. \(c\) 越界；
  2. \(x,y\) 越界；
  3. \((x,y)\) 位置已被覆盖；
  4. \((x,y)\) 位置从未被覆盖。

\(\text{upd 2023.8.19}\)：增加样例解释。

样例解释

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
/*
n = 2时，无论公主在哪个格子，我们都可以用一块毯子填满

n = 4的情况，首先，显然可以将4 * 4的盘面划分成4个2 * 2的小盘面，其中一块已经存在一个障碍了

而我们只需在正中间的2 * 2方格中放入一块地毯，就可以使所有小盘面都有一个障碍

回归到n=2的情况了
*/
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll x,y,len; int k;

void solve(ll x,ll y,ll a,ll b,ll l)
{
    if(l==1) return;
    if(x-a<=l/2-1 && y-b<=l/2-1)
    {
        printf("%lld %lld 1\n",a+l/2,b+l/2);
        solve(x,y,a,b,l/2);
        //分为四部分
        ///每一部分有一个障碍
        //直接弄中间
        //刚好符合
        //下面同理
        solve(a+l/2-1,b+l/2,a,b+l/2,l/2);
        solve(a+l/2,b+l/2-1,a+l/2,b,l/2);
        solve(a+l/2,b+l/2,a+l/2,b+l/2,l/2);
    }
    //用左上角
    else if(x-a<=l/2-1 && y-b>l/2-1)
    {
        printf("%lld %lld 2\n",a+l/2,b+l/2-1);
        solve(a+l/2-1,b+l/2-1,a,b,l/2);
        solve(x,y,a,b+l/2,l/2);
        solve(a+l/2,b+l/2-1,a+l/2,b,l/2);
        solve(a+l/2,b+l/2,a+l/2,b+l/2,l/2);
    }
    //左下角
    else if(x-a>l/2-1 && y-b<=l/2-1)
    {
        printf("%lld %lld 3\n",a+l/2-1,b+l/2);
        solve(a+l/2-1,b+l/2-1,a,b,l/2);
        solve(a+l/2-1,b+l/2,a,b+l/2,l/2);
        solve(x,y,a+l/2,b,l/2);
        solve(a+l/2,b+l/2,a+l/2,b+l/2,l/2);
    }
    //右上角
    else
    {
        printf("%lld %lld 4\n",a+l/2-1,b+l/2-1);
        solve(a+l/2-1,b+l/2-1,a,b,l/2);
        solve(a+l/2-1,b+l/2,a,b+l/2,l/2);
        solve(a+l/2,b+l/2-1,a+l/2,b,l/2);
        solve(x,y,a+l/2,b+l/2,l/2);
    }
}
//右下角
int main()
{
cin>>k>>x>>y;
    len=pow(2,k);
    solve(x,y,1,1,len);

}

[USACO04OPEN] MooFest G

题目背景

P5094 [USACO04OPEN] MooFest G 加强版

题目描述

约翰的 \(n\) 头奶牛每年都会参加“哞哞大会”。

哞哞大会是奶牛界的盛事。集会上的活动很多，比如堆干草，跨栅栏，摸牛仔的屁股等等。

它们参加活动时会聚在一起，第 \(i\) 头奶牛的坐标为 \(x_i\)，没有两头奶牛的坐标是相同的。

奶牛们的叫声很大，第 \(i\) 头和第 \(j\) 头奶牛交流，会发出 \(\max\{v_i,v_j\}\times |x_i − x_j |\) 的音量，其中 \(v_i\) 和 \(v_j\) 分别是第 \(i\) 头和第 \(j\) 头奶牛的听力。

假设每对奶牛之间同时都在说话，请计算所有奶牛产生的音量之和是多少。

输入格式

第一行：单个整数 \(n\)，\(1\le n\le2\times 10^4\)

第二行到第 \(n + 1\) 行：第 \(i + 1\) 行有两个整数 \(v_i\) 和 \(x_i\)（\(1\le v_i,x_i\le2\times 10^4\)）。

输出格式

单个整数：表示所有奶牛产生的音量之和

样例 #1

样例输入 #1

1
2
3
4
5
4
3 1
2 5
2 6
4 3

样例输出 #1

1
57
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//题出水了，可以暴力
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int n,m;
long long ans;
struct node             //结构体存储。
{
	int v,x;
}e[1000010];
int main() 
{
	scanf("%d",&n);
	for(int i=1;i<=n;++i) cin>>e[i].v>>e[i].x;
	for(int i=1;i<=n;++i) 
	for(int j=i+1;j<=n;++j)         //n方枚举累加。
	ans+=max(e[i].v,e[j].v)*abs(e[i].x-e[j].x);
	cout<<ans<<'\n';
	return 0;
}

由cdq分治的标签，那就学一下罢

用于解决离线或不强制在线问题中简化一层树结构的实用性分治算法

使用cdq分治的条件：

  • 修改操作对询问的贡献独立，修改操作相互不影响
  • 题目可以使用离线算法，不必强制在线（询问次数可以保存在数组）

cdq分治的性质：

  • cdq分治通过对时间复杂度增加一个log来降维
  • cdq可以用来代替复杂的数据结构
  • 在cdq分治中，对于划分出来的两个区间，前一个子问题需要用来解决后一个子问题。

CDQ分治主要思想还是分治的思想，即递归处理小范围信息，之后将处理的信息合并上传。一般来说，都是先处理左区间，之后用左区间更新右区间，顺便更新答案，然后处理右区间，之后再将两个区间的信息合并。

使用步骤：

  • 将整个操作序列分为两个长度相等的部分。
  • 递归处理前一部分的子问题（治1）
  • 计算前一部分子问题的修改操作对后一部分子问题的影响（治2）
  • 递归处理后一部分的子问题（治3）

究其原理，好比归并排序的计算左边块对右边块的贡献

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//归并排序求逆序对
void merge(int l,int r){
    if(l==r) return;
    int mid=(l+r)/2;
    merge(l,mid),merge(mid+1,r);
    int len=l,j=l;
    for(int i=mid+1;i<=r;i++){
        while(j<=mid&&a[j]<=a[i]) tmp[len++]=a[j++];
        tmp[len++]=a[i];
        ans+=mid-j+1;//计算左边对右边的贡献
    }
    while(j<=mid) tmp[len++]=a[j++];
    for(int i=l;i<=r;i++) a[i]=tmp[i]; 
}

看一道二维偏序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//二维偏序问题
void merge(int l,int r){
    //核心代码
    if(l==r)return;
    int mid=(l+r)>>1;
    merge(l,mid),merge(mid+1,r);
    int j=l,len=l;
    for(int i=mid+1;i<=r;i++){
        while(j<=mid&&a[i].y>=a[j].y){
            if(a[j].x==a[i].x&&a[j].y==a[i].y) break;
            j++;
        }
        a[i].num+=j-l;
    }
    sort(a+l,a+1+r,cmp);
}

[BJOI2016] 回转寿司

题目描述

酷爱日料的小Z经常光顾学校东门外的回转寿司店。在这里，一盘盘寿司通过传送带依次呈现在小Z眼前。

不同的寿司带给小Z的味觉感受是不一样的，我们定义小Z对每盘寿司都有一个满意度。

例如小Z酷爱三文鱼，他对一盘三文鱼寿司的满意度为 \(10\)；小Z觉得金枪鱼没有什么味道，他对一盘金枪鱼寿司的满意度只有 \(5\)；小Z最近看了电影《美人鱼》，被里面的八爪鱼恶心到了，所以他对一盘八爪鱼刺身的满意度是 \(-100\)。

特别地，小Z是个著名的吃货，他吃回转寿司有一个习惯，我们称之为“狂吃不止”。具体地讲，当他吃掉传送带上的一盘寿司后，他会毫不犹豫地吃掉它后面的寿司，直到他不想再吃寿司了为止。

今天，小Z再次来到了这家回转寿司店，\(N\) 盘寿司将依次经过他的面前。其中，小Z对第 \(i\) 盘寿司的满意度为\(a_i\)。

小Z可以选择从哪盘寿司开始吃，也可以选择吃到哪盘寿司为止。他想知道共有多少种不同的选择，使得他的满意度之和不低于 \(L\)，且不高于 \(R\)。

注意，虽然这是回转寿司，但是我们不认为这是一个环上的问题，而是一条线上的问题。即，小Z能吃到的是输入序列的一个连续子序列；最后一盘转走之后，第一盘并不会再出现一次。

输入格式

第一行三个正整数 \(N,L,R\)，表示寿司盘数，满意度的下限和上限。
第二行包含 \(N\) 个整数 \(a_i\)，表示小Z对寿司的满意度。

输出格式

一行一个整数，表示有多少种方案可以使得小Z的满意度之和不低于 \(L\) 且不高于 \(R\)。

样例 #1

样例输入 #1

1
2
5 5 9
1 2 3 4 5

样例输出 #1

1
6

提示

【数据范围】

\(1\le N \le 10^5\)
\(|a_i| \le 10^5\)
\(0\le L,R \le 10^9\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//核心代码
void merge(int l,int r){
    if(l==r) return;
    int mid=(l+r)/2;
    merge(l,mid),merge(mid+1,r);
    for(int j=l,i=mid+1;i<=r;i++){
        while(j<=mid&&sum[i]-sum[j]>=L) j++;
        ans+=j-l;
    }
    for(int j=l,i=mid+1;i<=r;i++){
        while(j<=mid&&sum[i]-sum[j]>R) j++;
        ans-=j-l;
    } 
    sort(sum+l,sum+1+r);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<bits/stdc++.h>//万能头文件
using namespace std;
long long L,R,ans,s[110000];
void cdq(int l,int r)
{
    if(l==r)return ;
    int mid=(l+r)/2;
    cdq(l,mid),cdq(mid+1,r);
    int head=l,tail=l-1;
    for(int i=mid+1;i<=r;i++)
    {
        while(tail+1<=mid && s[i]>=s[tail+1]+L)tail++;
        while(head<=mid && s[i]>s[head]+R)head++;
        ans+=tail-head+1;
    }
    sort(s+l,s+r+1);
}
//
int main()
{
    int n;
    cin>>n>>L>>R;
    for(int i=1;i<=n;i++)
    {
        int x;
        cin>>x;
        s[i]=s[i-1]+x;//前缀和
    }
    cdq(0,n);
    cout<<ans;
    return 0;
}

【模板】三维偏序（陌上花开）

题目背景

这是一道模板题，可以使用 bitset，CDQ 分治，KD-Tree 等方式解决。

题目描述

有 $ n $ 个元素，第 $ i $ 个元素有 $ a_i,b_i,c_i $ 三个属性，设 $ f(i) $ 表示满足 $ a_j a_i $ 且 $ b_j b_i $ 且 $ c_j c_i $ 且 $ j i $ 的 \(j\) 的数量。

对于 $ d ZAB-Frog

题面翻译

有 \(n\) 个点，升序给出每个点到起点的距离。有编号为 \(1 \sim n\) 的 \(n\) 只青蛙分别在第 \(1 \sim n\) 个点上，每次它们会跳到距离自己第 \(k\) 远的点上。

如果有相同距离的点，就跳到下标更小的点上。

求跳 \(m\) 次之后，第 \(i\) 只的青蛙在哪个点上。

输入共一行三个整数：代表 \(n, k, m\)。

输出共一行 \(n\) 个整数，代表每只青蛙最终所处在的点。

样例 #1

样例输入 #1

1
2
5 2 4
1 2 4 7 10

样例输出 #1

1
1 1 3 1 1

提示

\(1 \le k \lt n \le 10^6\)，\(1 \le m \le 10^{18}\)，\(1 \le p_1 \lt p_2 \lt ... \lt p_n \le 10^{18}\)

k 是固定的，所以可以先预处理，对于每个点 i，跳一次之后的位置nexti.

主要是k步知道，我们可以预处理出每一个位置怎么跳

这个预处理采取的是单调队列，如果右边还可以移动，还是先向右边移动

这样保证正确性，两头肯定就是我们的答案，因为我们控制了区间长度

倍增的过程，主要是next数组的快速幂这个很有精神

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
ll n,k,m;
const int N=1e6+100;
ll a[N];
ll nxt[N];
ll  ans[N];
ll temp[N];
int main()
{
	cin>>n>>k>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	int head=1,tail=k+1;
	//区间，要移动的区间
	//如果右边还可以再移动，那就向右边移动，两个++；
	nxt[1]=k+1;
	for(int i=2;i<=n;i++)
	{
		while(a[i]-a[head]>a[tail+1]-a[i]&&tail+1<=n)
		{
			head++;
			tail++;
		}
		if(a[i]-a[head]>=a[tail]-a[i])
		{
			nxt[i]=head;
		}
		else
		{
			nxt[i]=tail;
		}	
	}
	for(int i=1;i<=n;i++)
	{
		ans[i]=i;
	}
	while(m)
	{
		if(m&1)
		{
		for(int i=1;i<=n;i++)
		{
			ans[i]=nxt[ans[i]];
		}	
		}
		memcpy(temp,nxt,sizeof temp);
		for(int i=1;i<=n;i++)
		{
			nxt[i]=temp[temp[i]];
			//类似于next数组的倍增
		}
	m>>=1;	
	}
	for(int i=1;i<=n;i++)
	{
		cout<<ans[i]<<' ';
	}	
}

[POI2011] WYK-Plot

题目描述

We call any sequence of points in the plane a plot.

We intend to replace a given plot \((P_1,\cdots,P_n)\) with another that will have at most \(m\) points (\(m\le n\)) in such a way that it "resembles" the original plot best.

The new plot is created as follows. The sequence of points \(P_1,\cdots,P_n\) can be partitioned into \(s\) (\(s\le m\)) contiguous subsequences:

\((P_{k_0+1},\cdots,P_{k_1}),(P_{k_1+1},\cdots,P_{k_2}),\cdots,(P_{k_{s-1}+1},\cdots,P_{k_s})\) where \(0=k_0<k_1<k_2<\cdots<k_s=n\),and afterwards each subsequence \((P_{k_{i-1}+1},\cdots,P_{k_i})\), for \(i=1,\cdots,s\),is replaced by a new point \(Q_i\).

In that case we say that each of the points \(P_{k_{i-1}+1},\cdots,P_{k_i}\) has been contracted to the point \(Q_i\).

As a result a new plot, represented by the points \(Q_1,\cdots,Q_s\), is created.

The measure of such plot's resemblance to the original is the maximum distance of all the points \(P_1,\cdots,P_n\) to the point it has been contracted to:

\(max_{i=1,\cdots,s}(max_{j=k_{i-1}+1,\cdots,k_i}(d(P_j,Q_i)))\) where \(d(P_j,Q_i)\) denotes the distance between \(P_j\) and \(Q_i\), given by the well-known formula:

\(d((x_1,y_1),(x_2,y_2))=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)

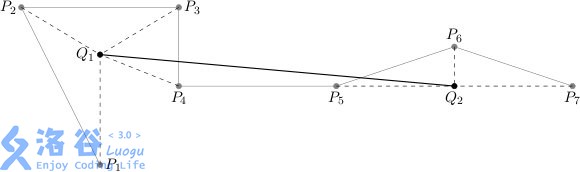
An exemplary plot \(P_1,\cdots,P_7\) and the new plot \((Q_1,Q_2)\), where \((P_1,\cdots,P_4)\) are contracted to \(Q_1\), whereas \((P_5,P_6,P_7)\) to \(Q_2\).

For a given plot consisting of \(n\) points, you are to find the plot that resembles it most while having at most \(m\) points, where the partitioning into contiguous subsequences is arbitrary.

Due to limited precision of floating point operations, a result is deemed correct if its resemblance to the given plot is larger than the optimum resemblance by at most \(0.000001\).

给定n个点，要求把n个点分成不多于m段，使得求出每段的最小覆盖圆的半径后，最大的半径最小。

输入格式

In the first line of the standard input there are two integers \(n\) and \(m\), \(1\le m\le n\le 100\ 000\), separated by a single space.

Each of the following \(n\) lines holds two integers, separated by a single space.

The \((i+1)\)-th line gives \(x_i\),\(y_i\),\(-1\ 000\ 000\le x_i,y_i\le 1\ 000\ 000\) denoting the coordinates \((x_i,y_i)\) of the point \(P_i\).

输出格式

In the first line of the standard output one real number \(d\) should be printed out, the resemblance measure of the plot found to the original one.

In the second line of the standard output there should be another integer \(s\), \(1\le s\le m\).

Next, the following \(s\) lines should specify the coordinates of the points \(Q_1,\cdots,Q_s\),one point per line.

Thus the \((i+2)\)-th line should give two real numbers \(u_i\) and \(v_i\), separated by a single space, that denote the coordinates \((u_i,v_i)\) of the point \(Q_i\).All the real numbers should be printed with at most 15 digits after the decimal point.

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
7 2
2 0
0 4
4 4
4 2
8 2
11 3
14 2

样例输出 #1

1
2
3
4
3.00000000
2
2.00000000 1.76393202
11.00000000 1.99998199

提示

给定n个点，要求把n个点分成不多于m段，使得求出每段的最小覆盖圆的半径后，最大的半径最小。

我看懂题解了！

$$ 设倍增得到最大的满足条件的区间长度为

2^ k ，那么我们二分的左端点为

min(n,i+2^(k+1) −1) $$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=100005;
int n,m,res[N][2],cnt,ci;
double eps=1e-10,R;
struct point{
    double x,y;
}a[N],b[N],O;
//点的结构体，a,b还有
point Mid(point A,point B)
{
    return (point){(A.x+B.x)/2,(A.y+B.y)/2};
}
//中点获取
double dist(point A,point B)
{
    return sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y));
}
//距离公式
void getO(point A,point B,point C)
{
    double aa,bb,cc,dd,ee,ff;
    aa=A.x-C.x;bb=A.y-C.y;
    cc=B.x-C.x;dd=B.y-C.y;
    ee=A.x*A.x+A.y*A.y-C.x*C.x-C.y*C.y;
    ff=B.x*B.x+B.y*B.y-C.x*C.x-C.y*C.y;
    O.x=(dd*ee-bb*ff)/(2*aa*dd-2*bb*cc);
    O.y=(aa*ff-cc*ee)/(2*aa*dd-2*bb*cc);
    R=dist(O,A);
}
//3点共圆，找到圆心和半径
void work(int l,int r)
{//随机增量求最小圆覆盖,O(r-l+1)
    int tot=0;
    for(int i=l;i<=r;i++) b[++tot]=a[i];
    for(int i=1;i<=tot;i++) swap(b[i],b[rand()%tot+1]);
    //求最小圆的预处理
    O=b[1],R=0;
    for(int i=1;i<=tot;i++)
    {
        if(dist(b[i],O)>R+eps)
        {//i不在圆内 
            O=b[i],R=0;
            for(int j=1;j<i;j++)
            {
                if(dist(b[j],O)>R+eps)
                {//j不在圆内
                    O=Mid(b[i],b[j]);
                    R=dist(O,b[i]);
                    for(int k=1;k<j;k++)
                        if(dist(b[k],O)>R+eps)
                            getO(b[i],b[j],b[k]);
                }
            }
        }
    }
}
bool check(double lim)
{
    cnt=0;
    int ans;
    for(int i=1;i<=n;i=ans+1)
    {
        int k;
        for(k=1;i+(1<<k)-1<=n;k++)
        {//k=0显然可行,从1开始 
            work(i,i+(1<<k)-1);
            if(R>lim+eps) break;
        }
        //求出那个能跳够跳多少步
        //
        ans=i;
        int l=i+(1<<(k-1))-1,r=min(n,i+(1<<k)-1);
        //左端点，然后二分
        while(l<=r)
        {
            int mid=(l+r)>>1;
            work(i,mid);
            if(R<lim+eps) l=mid+1,ans=mid;
            else r=mid-1;
        }
        //然后进行二分出哪个符合
        cnt++;
        res[cnt][0]=i,res[cnt][1]=ans;
        if(cnt>m) return 0;
    }
    return 1;
}
int main(){
    srand(20031128);
    cin>>n>>m;
    for(int i=1;i<=n;i++){
     cin>>a[i].x>>a[i].y;
    }
    work(1,n);
    //先求出最小圆涵盖所有点
    double l=0,r=R;
    //进行二分
    if(m>1)
    {
        ci=50;
        while(ci--&&r-l>eps)
        {
            double mid=(l+r)/2;
            if(check(mid)) r=mid;
            else l=mid;
        }
    }
    check(r);
    //求O,也就是圆心
    printf("%.8lf\n",r);
    cout<<cnt<<'\n';
    //分为几段
    for(int i=1;i<=cnt;i++)
    {
        work(res[i][0],res[i][1]);
        //输出
        printf("%.8lf %.8lf\n",O.x,O.y);
    }
}

[SCOI2015] 国旗计划

题目描述

A 国正在开展一项伟大的计划 —— 国旗计划。这项计划的内容是边防战士手举国旗环绕边境线奔袭一圈。这项计划需要多名边防战士以接力的形式共同完成，为此，国土安全局已经挑选了 \(N\) 名优秀的边防战上作为这项计划的候选人。

A 国幅员辽阔，边境线上设有 \(M\) 个边防站，顺时针编号 \(1\) 至 \(M\)。每名边防战士常驻两个边防站，并且善于在这两个边防站之间长途奔袭，我们称这两个边防站之间的路程是这个边防战士的奔袭区间。\(N\) 名边防战士都是精心挑选的，身体素质极佳，所以每名边防战士的奔袭区间都不会被其他边防战士的奔袭区间所包含。

现在，国十安全局局长希望知道，至少需要多少名边防战士，才能使得他们的奔袭区间覆盖全部的边境线，从而顺利地完成国旗计划。不仅如此，安全局局长还希望知道更详细的信息：对于每一名边防战士，在他必须参加国旗计划的前提下，至少需要多少名边防战士才能覆盖全部边境线，从而顺利地完成国旗计划。

输入格式

第一行，包含两个正整数 \(N,M\)，分别表示边防战士数量和边防站数量。

随后 \(N\) 行，每行包含两个正整数。其中第 \(i\) 行包含的两个正整数 \(C_i\)、\(D_i\) 分别表示 \(i\) 号边防战士常驻的两个边防站编号，\(C_i\) 号边防站沿顺时针方向至 \(D_i\) 号边防站力他的奔袭区间。数据保证整个边境线都是可被覆盖的。

输出格式

输出数据仅 \(1\) 行，需要包含 \(N\) 个正整数。其中，第 \(j\) 个正整数表示 \(j\) 号边防战士必须参加的前提下至少需要多少名边防战士才能顺利地完成国旗计划。

样例 #1

样例输入 #1

1
2
3
4
5
4 8
2 5
4 7
6 1
7 3

样例输出 #1

1
3 3 4 3

提示

\(N\leqslant 2×10^5,M<10^9,1\leqslant C_i,D_i\leqslant M\)。

几个月前被吊打的题如今依然被吊打（） \[ f[i][j]=f[f[i][j−1]][j−1] \]

$$

f[i][0] ，就可以求出全部的

f[i][j]。

f[i][0] 即每个区间后选的第一个区间。 $$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n,m,a,b,cnt,f[2 * N][25],ans[N];
struct line
{
	int id,l,r;
	bool operator < (const line &k) const 
	{
	    return r < k.r;
	}
}L[4*N];
void pre()
{
	int p2 = 1;
		//跳一步能跳到哪里呢
	for(int p1 = 1; p1 <= 2 * n; p1++)
	{
		while(p2 <= 2 * n)
		{
			if(L[p2].l > L[p1].r) break;
			//如果已经不能再跳了，就左端点已经比他的右端点大了就停下来
			p2++;
		}
		p2--;
		f[p1][0] = p2;
		//记录能跳到的那个军人
	}
	for(int j = 1; (1 << j) <= 2 * n; j++)
    {
    	for(int i = 1; i <= 2 * n; i++)
    		if(f[i][j - 1]) f[i][j] = f[f[i][j - 1]][j - 1];
	}
	//倍增处理
}
int main()
{
	cin>>n>>m;
	for(int i = 1; i <= n; i++)
	{
		cin>>a>>b;
		//输入两个端点
		if(b < a) b += m;
		//如果左端点大于右端点，给右端点+m
		L[i].id = i;
		L[i].l = a;
		L[i].r = b;
		//记录
	}
	sort(L + 1,L + n + 1);
	//排序，由于按照右端点排序，贪心，能更远要跳更远
	for(int i = 1; i <= n; i++)
	//接下来得到我们最后要处理的数组
	{
		L[i + n].id = 0;
		L[i + n].l = L[i].l + m;
		L[i + n].r = L[i].r + m;
	}
	pre();
	//进入倍增
	for(int k = 1; k <= n; k++)
	{
		int tp = k,cnt = 1;
		//记录一个初始值和一个计数器
		for(int i = 20; i >= 0; i--)
		{
			if(f[tp][i] > 0 && L[f[tp][i]].r - L[k].l < m) 
			{
				tp = f[tp][i];
				cnt += (1 << i);
				//如果这个值能到，并且小于m，就加上，然后从这个点开始跳跃
			}
		}
		ans[L[k].id] = cnt + 1;
		//最后加上
	}
	for(int i = 1; i <= n; i++)
	    cout<<ans[i]<<' ';
}

忠诚

题目描述

老管家是一个聪明能干的人。他为财主工作了整整 \(10\) 年。财主为了让自已账目更加清楚，要求管家每天记 \(k\) 次账。由于管家聪明能干，因而管家总是让财主十分满意。但是由于一些人的挑拨，财主还是对管家产生了怀疑。于是他决定用一种特别的方法来判断管家的忠诚，他把每次的账目按 \(1, 2, 3 \ldots\) 编号，然后不定时的问管家问题，问题是这样的：在 \(a\) 到 \(b\) 号账中最少的一笔是多少？为了让管家没时间作假，他总是一次问多个问题。

输入格式

输入中第一行有两个数 \(m, n\)，表示有 \(m\) 笔账 \(n\) 表示有 \(n\) 个问题。

第二行为 \(m\) 个数，分别是账目的钱数。

后面 \(n\) 行分别是 \(n\) 个问题，每行有 \(2\) 个数字说明开始结束的账目编号。

输出格式

在一行中输出每个问题的答案，以一个空格分割。

样例 #1

样例输入 #1

1
2
3
4
5
10 3
1 2 3 4 5 6 7 8 9 10
2 7
3 9
1 10

样例输出 #1

1
2 3 1

提示

对于 \(100\%\) 的数据，\(m \leq 10^5\)，\(n \leq 10^5\)。

ST表板子题目，贴个板子就过

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
using ll=long long;
int st[N][20];
int lg[N];
int n,m;
int main()
{
    ios::sync_with_stdio(0);
 	cin.tie(0);
 	cout.tie(0);
    cin>>n>>m;
    lg[1]=0;
    for(int i=2;i<=n;i++)
    {
        lg[i]=lg[i>>1]+1;
    }
    for(int i=1;i<=n;i++)
    {
        cin>>st[i][0];
    }
    for(int j=1;j<=lg[n];j++)
    {
        for(int i=1;i+(1<<j)-1<=n;i++)
        {
            st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);
		}
	}
    int l,r;
    while(m--)
    {
        cin>>l>>r;
        int t=lg[r-l+1];
        cout<<min(st[l][t],st[r-(1<<t)+1][t])<<' ';
    }  
}

[CCC2019] Triangle: The Data Structure

题目背景

在 Shuchong 的平行宇宙里，计算机学中的最重要的数据结构就是三角形。
注：因为原数据包太大，故这题缩减了一些数据，具体缩减的数据点如下：

  • Subtask 1：1 ~ 10
  • Subtask 2：1 ~ 10

所以此题拥有的测试点为：

  • Subtask 1：11 ~ 26
  • Subtask 2：11 ~ 24

若想测试本题没有的测试点请到 此处 测试。

题目描述

大小为 \(m\) 的一个三角形由 \(m\) 行组成，第 \(i\) 行包含 \(i\) 个元素。
并且，这些行必须排为等边三角形的形状。
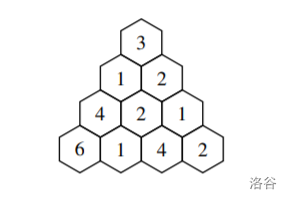
比如说，以下是一个 \(m=4\) 的三角形。

每个三角形还包含子三角形。
比如说上面这个三角形，包含：

  • \(10\) 个大小为 \(1\) 的三角形。
  • \(6\) 个大小为 \(2\) 的三角形。
  • \(3\) 个大小为 \(3\) 的三角形。

注意，每个三角形都是自身的子三角形。
现在给定一个大小为 \(n\) 的三角形，求对于每个大小为 \(k\) 的子三角形，子三角形内几个数的最大值的和。

输入格式

第一行两个整数 \(n,k\) 代表三角形的大小和要求的子三角形的大小。
接下来 \(n\) 行第 \(i\) 行有 \(i\) 个整数代表这个三角形。

输出格式

一行一个整数代表对于每个大小为 \(k\) 的子三角形，子三角形内几个数的最大值的和。

样例 #1

样例输入 #1

1
2
3
4
5
4 2
3
1 2
4 2 1
6 1 4 2

样例输出 #1

1
23

提示

数据规模与约定

  • Subtask 1（25 pts）：\(n \le 1000\)。
  • Subtask 2（75 pts）：无特殊限制。

对于 \(100\%\) 的数据，\(1 \le k \le n \le 3000\)，$0 $ 三角形内每个数 \(\le 10^9\)。

说明

翻译自 CCC 2019 Senior T5 Triangle: The Data Structure。
翻译者：@一只书虫仔。

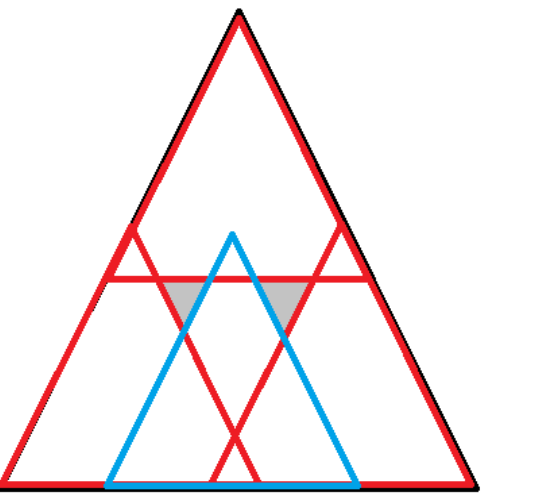
给你一个高度为n的数字金字塔，求它的所有高度为k的子金字塔的最大值的总和。

为了取到三个顶点，我们首先取三个正的着三角形

然后中间那个也直接用3个去取，然后答案倍增处理

（因为这句话看了半小时没看懂）

image-20240225151000090 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=3005;
int n,h,val[N][N],st[N][N][2],lg[N],k;
ll ans;
int query(int x,int y)
{
	int l=x+h-1,r=y+h-1; 
	int u=k&1;
	int ans=max(st[x][y][u],max(st[l-(1<<k)+1][y][u],st[l-(1<<k)+1][r-(1<<k)+1][u]));
	if(k<=1)
	return ans;
	int cha=(h-(1<<k))>>1;
	ans=max(max(ans,st[l-(1<<k)+1][y+cha][u]),max(st[x+cha][y][u],st[x+cha][y+cha][u]));
	return ans; 
}
//记录答案这里，自己推把（）也是和下面类似的
int main()
{
	cin>>n>>h;
	k=log2(h);
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=i;j++)
		{
			cin>>val[i][j];
			st[i][j][0]=val[i][j];
			//原地，一步而已此时对于ST数组而言
		}
	}
	for(int t=1;t<=k;t++)
	{
		int u=t&1,v=u^1;
		//滚动ST表的实现由来
		//不断1，0交替进行，实现滚动的效果
		//原因：这题的询问子三角形大小是固定的，因此我们的 ST 表可以滚动起来，保留 log2k 的值就可以了
		for(int i=1;i+(1<<t)-1<=n;i++)
		{
			for(int j=1;j<=i;j++){
				st[i][j][u]=max(max(st[i][j][v],st[i+(1<<t-1)][j][v]),st[i+(1<<t-1)][j+(1<<t-1)][v]);
				//对应最好找对的三个三角形
				if(t>1)
				{
st[i][j][u]=max(max(st[i][j][u],st[i+(1<<t-1)][j+(1<<t-2)][v]),max(st[i+(1<<t-2)][j][v],st[i+(1<<t-2)][j+(1<<t-2)][v]));
				}
				//对应中间那三个三角形
			}
		}
	}
	//对应上图的5个图形
	
	/*
4 2
3
1 2
4 2 1
6 1 4 2
	*/	
	for(int i=1;i<=n-h+1;i++)
	{
		for(int j=1;j<=i;j++)
		{
			ans+=query(i,j);
		}
	}
	cout<<ans;
}

[JOISC 2021 Day4] イベント巡り 2 (Event Hopping 2)

题目背景

因洛谷限制，本题不予评测每个 Subtask 的第 1 ~ 20 个测试点，您可以 点此 下载所有数据自行评测或在 这里 测试，若您希望写本题题解，建议您在通过 本题 与 每个 Subtask 前 20 个测试点 之后再写题解。

题目描述

IOI Park 将有 \(n\) 场活动。

这些活动的编号从 \(1\) 到 \(n\)。 活动 \(i\) 从时间 \(L_i+10^{-1}\) 到时间 \(R_i-10^{-1}\) 举行。数据保证 \(L_i\) 和 \(R_i\) 是整数。

JOI 君决定参加其中的 \(k\) 个活动。但是，JOI 君不能在中间加入或离开每个活动。在两个活动场所间移动的时间忽略不计。

JOI 君希望参加编号较小的活动。严格来说，JOI 君参加的 \(k\) 个活动的编号依次为 \(a_1,\cdots,a_k\)，其中 \(1 \le a_1 < \cdots < a_k \le n\)。如果序列 \((a_1, \cdots, a_k)\) 的编号小于 \((b_1, \cdots, b_k)\)，当且仅当存在 \(j\ (1 \le j \le k)\) 满足在区间 \([1,j-1]\) 里的所有 \(l\) 都有 \(a_l=b_l\) 和 \(a_j<b_j\)。

给出每个活动的信息和 JOI 君参加的活动个数 \(k\)，判断 JOI 君是否可以参加 \(k\) 个活动，如果可以，输出所有的 \(k\) 个活动的编号。

输入格式

第一行，两个正整数 \(n,k\)。

第 \(2 \sim n + 1\) 行，每行 \(2\) 个正整数，\(L_i, R_i\)。

输出格式

如果 JOI 君可以参加 \(k\) 个活动：

  • 输出 \(k\) 行。
  • 我们设 JOI 君参与的 \(k\) 个活动的编号为 \(a_1, a_2, \cdots, a_k\ (1\le a_1 < \cdots < a_k \le n）\)，你需要在第 \(j\) 行输出 \(a_j\ (1\le j \le k)\)。 请注意，序列 \((a_1, \cdots, a_k)\) 必须是 最小字典序。

如果 JOI 君无法参加 \(k\) 个活动，输出 \(\texttt{-1}\)。

样例 #1

样例输入 #1

1
2
3
4
5
6
5 4
1 3
2 5
8 9
6 8
10 15

样例输出 #1

1
2
3
4
1
3
4
5

样例 #2

样例输入 #2

1
2
3
4
5
4 3
1 4
3 5
4 9
7 10

样例输出 #2

1
-1

样例 #3

样例输入 #3

1
2
3
4
5
6
7
8
9
10
11
10 6
77412002 93858605
244306432 318243514
280338037 358494212
439397354 492065507
485779890 529132783
571714810 632053254
659767854 709114867
718405631 733610573
786950301 815106357
878719468 899999649

样例输出 #3

1
2
3
4
5
6
1
2
4
6
7
8

样例 #4

样例输入 #4

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
20 16
250732298 258217736
26470443 34965880
252620676 260043105
692063405 697656580
497457675 504191511
391372149 397942668
858168758 867389085
235756850 241022021
585764751 593366541
207824318 217052204
661682908 671226688
886273261 892279963
770109416 778960597
264372562 270395107
176883483 186662376
509929119 519063796
109491630 118520141
162731982 168101507
662727316 668317158
757072772 765493222

样例输出 #4

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
4
5
6
7
8
9
10
11
12
13
14
15
16
17

提示

样例 #1 解释

有 \(2\) 种方式可以参加正好 \(4\) 个活动。

  • 参加 \(1, 3, 4, 5\)；
  • 参加 \(2, 3, 4, 5\)。

数列 \((1,3,4,5)\) 比数列 \((2, 3, 4, 5)\) 字典序小，所以输出 \(1, 3, 4, 5\)。

样例 #2 解释

无论怎么选择都不可能正好参加 \(3\) 个活动，所以输出 \(\tt -1\)。

样例 #3 解释

本样例满足所有 Subtask 的条件。

数据规模与约定

因洛谷限制，本题不予评测每个 Subtask 的第 \(1\sim 20\) 个测试点。

本题采用 Subtask 计分法。

Subtask 分值占比百分率 \(n\) \(L_i\)
\(1\) \(7\%\) / \(L_i \le L_{i+1}\ (1 \le i \le n − 1)\)
\(2\) \(1\%\) \(\le20\) /
\(3\) \(31\%\) \(\le 3 \times 10^3\) /
\(4\) \(61\%\) / /

注：斜线表示无特殊限制。

对于 \(100\%\) 的数据：

  • \(1\le n\le 10^5\)；
  • \(1 \le k \le n\)；
  • \(1\le L_i < R_i \le 10^9 (1\le i \le n)\)。

说明

本题译自 第２０回日本情報オリンピック 2020/2021春季トレーニング合宿 - 競技 4 - T1 日文题面。

珂朵莉树（Chtholly Tree）起源于[CF896C]，那道题要求我们实现一种数据结构，可以较快地实现：

  • 区间加
  • 区间赋值
  • 求区间第k大值
  • 求区间n次方和

珂朵莉树的思想在于随机数据下的区间赋值操作很可能让大量元素变为同一个数。所以我们以三元组<l,r,v>的形式保存数据（区间 [l,r] 中的元素的值都是v）：

1
2
3
4
5
6
7
struct node
{
    ll l, r;
    mutable ll v; // 这里mutable要写不然可能会CE
    node(ll l, ll r, ll v) : l(l), r(r), v(v) {} // 构造函数
    bool operator<(const node &o) const { return l < o.l; } // 重载小于运算符
};

把这些三元组存储到set里

1
set<node> tree;

我们进行区间操作时并不总是那么幸运，可能会把原本连续的区间断开。我们需要一个函数来实现“断开”的操作，把<l,r,v>断成<l,pos-1,v>和<pos,r,v>：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
auto split(ll pos)
// 若不支持C++14，auto须改为set<node>::iterator
{
    auto it = tree.lower_bound(node(pos, 0, 0)); // 寻找左端点大于等于pos的第一个节点
    // 若不支持C++11，auto须改为set<node>::iterator
    if (it != tree.end() && it->l == pos) // 如果已经存在以pos为左端点的节点，直接返回
        return it;
    it--; // 否则往前数一个节点
    ll l = it->l, r = it->r, v = it->v;
    tree.erase(it); // 删除该节点
    tree.insert(node(l, pos - 1, v)); // 插入<l,pos-1,v>和<pos,r,v>
    return tree.insert(node(pos, r, v)).first; // 返回以pos开头的那个节点的迭代器
                                              // insert默认返回值是一个pair，第一个成员是我们要的
}

珂朵莉树的精髓在于区间赋值。而区间赋值操作的写法也极其简单：

1
2
3
4
5
6
void assign(ll l, ll r, ll v)
{
    auto end = split(r + 1), begin = split(l); // 顺序不能颠倒，否则可能RE
    tree.erase(begin, end); // 清除一系列节点
    tree.insert(node(l, r, v)); // 插入新的节点
}

其他操作

区间加

1
2
3
4
5
6
void add(int l, int r, LL val)
{
    IT itl = split(l),itr = split(r+1);
    for (; itl != itr; ++itl) 
        itl->v += val;
}

Physical Education Lessons

题面翻译

题意：

Alex高中毕业了，他现在是大学新生。虽然他学习编程，但他还是要上体育课，这对他来说完全是一个意外。快要期末了，但是不幸的Alex的体育学分还是零蛋！

Alex可不希望被开除，他想知道到期末还有多少天的工作日，这样他就能在这些日子里修体育学分。但是在这里计算工作日可不是件容易的事情：

从现在到学期结束还有 \(n\) 天(从 \(1\) 到 \(n\) 编号)，他们一开始都是工作日。接下来学校的工作人员会依次发出 \(q\) 个指令，每个指令可以用三个参数 \(l,r,k\) 描述：

  • 如果 \(k=1\)，那么从 \(l\) 到 \(r\) （包含端点）的所有日子都变成非工作日。

  • 如果 \(k=2\)，那么从 \(l\) 到 \(r\) （包含端点）的所有日子都变成工作日。

帮助Alex统计每个指令下发后，剩余的工作日天数。

输入格式：

第一行一个整数 \(n\)，第二行一个整数 \(q\) \((1\le n\le 10^9,\;1\le q\le 3\cdot 10^5)\)，分别是剩余的天数和指令的个数。

接下来 \(q\) 行，第 \(i\) 行有 \(3\) 个整数 \(l_i,r_i,k_i\)，描述第 \(i\) 个指令 \((1\le l_i,r_i\le n,\;1\le k\le 2)\)。

输出格式：

输出 \(q\) 行，第 \(i\) 行表示第 \(i\) 个指令被下发后剩余的工作日天数。

Translated by 小粉兔

题目描述

This year Alex has finished school, and now he is a first-year student of Berland State University. For him it was a total surprise that even though he studies programming, he still has to attend physical education lessons. The end of the term is very soon, but, unfortunately, Alex still hasn't attended a single lesson!

Since Alex doesn't want to get expelled, he wants to know the number of working days left until the end of the term, so he can attend physical education lessons during these days. But in BSU calculating the number of working days is a complicated matter:

There are $ n $ days left before the end of the term (numbered from $ 1 $ to $ n $ ), and initially all of them are working days. Then the university staff sequentially publishes $ q $ orders, one after another. Each order is characterised by three numbers $ l $ , $ r $ and $ k $ :

  • If $ k=1 $ , then all days from $ l $ to $ r $ (inclusive) become non-working days. If some of these days are made working days by some previous order, then these days still become non-working days;
  • If $ k=2 $ , then all days from $ l $ to $ r $ (inclusive) become working days. If some of these days are made non-working days by some previous order, then these days still become working days.

Help Alex to determine the number of working days left after each order!

输入格式

The first line contains one integer $ n $ , and the second line — one integer $ q $ ( $ 1<=n<=10^{9} $ , $ 1<=q<=3·10^{5} $ ) — the number of days left before the end of the term, and the number of orders, respectively.

Then $ q $ lines follow, $ i $ -th line containing three integers $ l_{i} $ , $ r_{i} $ and $ k_{i} $ representing $ i $ -th order ( $ 1<=l_{i}<=r_{i}<=n $ , $ 1<=k_{i}<=2 $ ).

输出格式

Print $ q $ integers. $ i $ -th of them must be equal to the number of working days left until the end of the term after the first $ i $ orders are published.

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
4
6
1 2 1
3 4 1
2 3 2
1 3 2
2 4 1
1 4 2

样例输出 #1

1
2
3
4
5
6
2
0
2
3
1
4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <bits/stdc++.h>
#define IT set<node>::iterator
using namespace std;
struct node
{
    int l,r;
    mutable bool v;
    node(int L, int R=-1, bool V=0):l(L), r(R), v(V) {}
    bool operator<(const node& o) const
    {
        return l < o.l;
    }
};
set<node> s;
int sum=0;
IT split(int pos)
{
    IT it = s.lower_bound(node(pos));
    if (it != s.end() && it->l == pos) 
        return it;
    --it;
    int L = it->l, R = it->r;
    bool V = it->v;
    s.erase(it);
    s.insert(node(L, pos-1, V));
    return s.insert(node(pos, R, V)).first;
}
void assign_val(int l,int r,bool val)
{
    IT itr = split(r+1), itl = split(l), it = itl;
    for( ;itl != itr; ++itl)
        sum-=itl->v*(itl->r-itl->l+1); //过程中顺带计算
    s.erase(it,itr);
    s.insert(node(l,r,val));
    sum+=val*(r-l+1); //过程中顺带计算
}
int main()
{
     ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
	int n,m;
    cin>>n>>m;
	s.insert(node(1,n,1));
	sum=n;
	while(m--)
	{
	int l,r,op;
        cin>>l>>r>>op;
		if(op==1) //修改
			assign_val(l,r,0);
		else
			assign_val(l,r,1);
		cout<<sum<<'\n';
	}
}

主要是 set 的应用

活动 \(i\) 为 \([x, y]\)，直接调用 set::find({x, y})，此时函数会返回一个与 \([x, y]\) 这个区间相交的区间。

set 会将相交的两段区间认为是相等的元素，这样做的好处是可以保证算法的正确性。
即，任何两个相交的元素都会被 set 认为相等，也就是会被自动去重。

问题二的求解

如果有一个 query 函数可以返回在 \([l, r]\) 这段区间里可以选择多少个活动，那么就可以通过在问题 1 中实现的维护空闲时间来解决这个问题。

如果选择了覆盖区间为 \([x, y]\) 的活动，那么这个查询就会变成： 

1
last - query(l, r) + query(l, x) + query(y, r);

如何实现 query 函数？

倍增思想可以用来实现。构造如下转移数组：
$ f[i][j] i 2^j $

递推关系： $ f[i][j] = f[f[i][j-1]][j-1], $ 其中，\(f[i][0]\) 表示从点 \(i\) 开始，挑选一个活动后所能到达的最靠左的坐标。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 100;
struct Seg
{
    int l, r; 
	// 区间的左右端点
    Seg(int x = 0, int y = 0) 
	// 构造函数，默认形参为 0
    {
        l = x;
        r = y;
    }
    bool operator<(const Seg &rhs) const 
	// 重载小于号，用于 set 的内部排序（不重载小于号，结构体不能放入 set）
    {
        return r < rhs.l;
    }
};
int n, k;
Seg s[N];           
// 存储所有的活动
vector<int> all;    
// 用于离散化
int f[2 * N][19];  
set<Seg> st;        
// 用 set 维护空余时间，对于这点上面已经描述过了
void get_f()
{
    memset(f, 0x3f, sizeof(f)); // 把整个矩阵初始化为最大值
    for (int i = 1; i <= n; i++) // 先通过所有活动的左右端点，赋上最初的初值
    {
        f[s[i].l][0] = min(f[s[i].l][0], s[i].r);
    }
    for (int i = all.size() - 1; i; i--) // 从右往左遍历离散化后的坐标，递推得出完整的第 0 列
    {
        f[i][0] = min(f[i][0], f[i + 1][0]);
    }
    // 用倍增板子，得出整个 f 矩阵
    for (int p = 1; p < 19; p++) // 外层循环枚举列
    {
        for (int i = 0; i < all.size(); i++) // 内层循环枚举行
        {
            // 如果往右选 2^(p-1) 个活动后跳到的坐标，是一个合法坐标才能进行递推
            // 否则，f[f[i][p - 1]][p - 1] 里的行号就是不合法的，调用后会数组越界
            if (f[i][p - 1] < all.size())
            f[i][p] = f[f[i][p - 1]][p - 1];
        }
    }
}

// 查询空闲区间 [l,r] 中最多能够选出几个活动
int query(int l, int r)
{
    int res = 0;
    int cur = l; // 初始位置位于左端点处
    for (int p = 18; ~p; p--)
    {
        if (f[cur][p] <= r)     // 往右选 2^p 个活动后不会超过右端点，那就选
        {
            cur = f[cur][p];    // 选了 2^p 个活动，跳到对应的位置
            res += (1 << p);    // 统计刚选上的 2^p 个活动
        }
    }
    return res; // 上述循环结束后 res 就是所求答案
}
// 用 x 与 y 构造出一个左端点为 x，右端点为 y 的元素，并将其返回
Seg make(int x, int y)
{
    Seg tmp(x, y);
    return tmp;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> k;
    for (int i = 1; i <= n; i++)    
	// 输入所有的活动
    {
        cin >> s[i].l >> s[i].r;
        all.push_back(s[i].l);      // 把每一个出现的左右端点放到 all 里，之后用于离散化
        all.push_back(s[i].r);
    }
    sort(all.begin(), all.end());               // 离散化前排序
    auto ed = unique(all.begin(), all.end());   // 离散化前去重
    all.erase(ed, all.end());                   // 把调用 unique 后放到最后的重复元素，直接删除，这样一来 all 的大小就是最右边的坐标值
    for (int i = 1; i <= n; i++)
    {
        s[i].l = lower_bound(all.begin(), all.end(), s[i].l) - all.begin(); // 令每个活动的端点变为离散化后的值
        s[i].r = lower_bound(all.begin(), all.end(), s[i].r) - all.begin();
    }
    get_f(); 
	// 得到 f 矩阵
    st.insert(make(0, all.size() - 1));
    vector<int> res;                        
	// res 里保存答案
    set<Seg>::iterator it;
    int last = query(0, all.size() - 1);    
	// 一开始，所有空余时间段内能够选择的活动数，就是整个坐标轴上能选的活动数
    for (int i = 1; i <= n && res.size() < k; i++)      
	// 从 1~n 遍历每一个活动，遍历完所有活动或已选活动数达到 k 个后退出循环
    {
        if ((it = st.find(s[i])) == st.end()) continue; 
		// 没有能与当前活动相交的空闲区间，直接跳过就好
        // it 现在指向的元素，就是与活动 i 相交的某一个元素
        if (s[i].l >= it->l && s[i].r <= it->r) 
		// 如果该元素完全包含了活动 i，则继续进行考虑，否则跳过就好
        {
            // 如果选完这个活动以后，剩下的空余时间里依然能选出足够的活动，那就选上这个活动
            if (last - query(it->l, it->r) + query(it->l, s[i].l) + query(s[i].r, it->r) >= k - res.size() - 1)
            {
                last = last - query(it->l, it->r) + query(it->l, s[i].l) + query(s[i].r, it->r);    
				// 剩余能选的活动数对应减少
                res.push_back(i);                                                                   
				// 把当前活动存入 res
                Seg t1(it->l, s[i].l), t2(s[i].r, it->r);   
				// 两个新的要插入的元素，即被活动 i 分割开来的两个区间
                st.erase(it);                               
				// 删除旧的元素
                st.insert(t1);                             
                st.insert(t2);
                 // 插入两个新元素
            }
        }
    }
    if (res.size() == k) // 退出循环后，如果已经选出了 k 个活动
    {
        for (auto j : res) // 输出选择的活动
        {
            cout << j << '\n';
        }
        return 0;
    }
        cout << -1;
        //不够选
}