动态规划的引入

[USACO1.5] [IOI1994]数字三角形 Number Triangles

题目描述

观察下面的数字金字塔。

写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

在上面的样例中，从 \(7 \to 3 \to 8 \to 7 \to 5\) 的路径产生了最大权值。

输入格式

第一个行一个正整数 \(r\) ,表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

输出格式

单独的一行,包含那个可能得到的最大的和。

样例 #1

样例输入 #1

1
2
3
4
5
6
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

样例输出 #1

1
30

提示

【数据范围】
对于 \(100\%\) 的数据，\(1\le r \le 1000\)，所有输入在 \([0,100]\) 范围内。

题目翻译来自NOCOW。

USACO Training Section 1.5

IOI1994 Day1T1

解释：

正着推要搜索，显然会陷入超时

于是我们考虑逆着推导

看样例分析：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
        7 
      3   8 
	8   1   0 
  2   7   4   4 
4   5   2   6   5

看样例我们可以更新倒数第二排，因为一定是从倒数第一排走过来的，因为都是正数，更相信后，就会等于
     7 
      3   8 
	8   1   0 
  7   12  10  10 
最后一行就没有用了
依次往上推
最后输出初始值就可以了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<iostream> 
#include<cstdio> 
#include<cmath> 
#include<algorithm>
using namespace std;  
int n;  
int a[1000][1000];  
int main()  
{       
    cin>>n;
	for(int i=0;i<n;i++)  
	for(int j=0;j<=i;j++)  
	cin>>a[i][j];
	for(int i=n-2;i>=0;i--)   
	{  
 		for(int j=0;j<=i;j++)
		a[i][j]+=max(a[i+1][j],a[i+1][j+1]); 
   
    } 
    cout<<a[0][0];
  
 }

不习惯从0开始看下面
    #include<bits/stdc++.h>
using namespace std;
long long n,a[1005][1005];
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	 for(int j=1;j<=i;j++) cin>>a[i][j];
	for(int i=n-1;i>=1;i--)
	 for(int j=1;j<=i;j++) a[i][j]+=max(a[i+1][j],a[i+1][j+1]);
	cout<<a[1][1];
	return 0;
}

[NOIP2005 普及组] 采药

题目描述

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是辰辰，你能完成这个任务吗？

输入格式

第一行有 \(2\) 个整数 \(T\)（\(1 \le T \le 1000\)）和 \(M\)（\(1 \le M \le 100\)），用一个空格隔开，\(T\) 代表总共能够用来采药的时间，\(M\) 代表山洞里的草药的数目。

接下来的 \(M\) 行每行包括两个在 \(1\) 到 \(100\) 之间（包括 \(1\) 和 \(100\)）的整数，分别表示采摘某株草药的时间和这株草药的价值。

输出格式

输出在规定的时间内可以采到的草药的最大总价值。

样例 #1

样例输入 #1

1
2
3
4
70 3
71 100
69 1
1 2

样例输出 #1

1
3

提示

【数据范围】

  • 对于 \(30\%\) 的数据，\(M \le 10\)；
  • 对于全部的数据，\(M \le 100\)。

【题目来源】

NOIP 2005 普及组第三题

01背包简介

01背包问题指有N件物品和一个容量为V的背包，每件物品都有一个价值和一个体积，目的是使用容量为V的背包装价值尽可能大的物品。01背包问题时最典型的动态规划问题之一，掌握01背包问题的动态规划解法很重要。

动态规划递推公式及一维数组实现 动态规划解法：定义一个二维数组dp,dp的第一维用于枚举物品数量，第二位用于枚举容量，所以dp[i][j]代表：在前i件物品中选取总容量不超过j的物品能够获得的最大价值。所以当递推结束后，dp[N] [V]就是我们要的答案。有递推公式如下： d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − w [ i ] ] + v [ i ] )

第i件物品只有2中状态：被选或者不被选(正因如此，所以才叫"01"背包)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
int dp[10000][10000];
int t[1000];
int v[1000];
int main()
	{
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <=m ; i++)
	{
		cin >> t[i] >> v[i];
	}
        for (int i = 1; i <= m; i++)
        for (int j = n; j >= 0; j--)
        {
            if (j >= t[i])
            {
                dp[i][j] = max(dp[i - 1][j - t[i]] + v[i], dp[i - 1][j]);
            }
            else
            {
                dp[i][j] = dp[i - 1][j];
            }
        }
cout<<dp[m][n];
    return 0;
	}





//压缩为一维要倒着枚举，不然会重复放东西，进阶为完全背包
一维代码

#include "stdio.h"
#include "iostream"
using namespace std;
int w[105], val[105];
int dp[1005];
int main()
{
    int t,m,res=-1;    
    scanf("%d%d",&t,&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&w[i],&val[i]);
    }
    for(int i=1;i<=m;i++) 
    {
        for(int j=t;j>=0;j--) 
        {
            if(j>=w[i])
            {
                dp[j]=max(dp[j-w[i]]+val[i], dp[j]);
            }
        }
    }    
    printf("%d",dp[t]);
    return 0;
}

[NOIP1996 提高组] 挖地雷

题目描述

在一个地图上有 \(N\ (N \le 20)\) 个地窖，每个地窖中埋有一定数量的地雷。同时，给出地窖之间的连接路径。当地窖及其连接的数据给出之后，某人可以从任一处开始挖地雷，然后可以沿着指出的连接往下挖（仅能选择一条路径），当无连接时挖地雷工作结束。设计一个挖地雷的方案，使某人能挖到最多的地雷。

输入格式

有若干行。

第 \(1\) 行只有一个数字，表示地窖的个数 \(N\)。

第 \(2\) 行有 \(N\) 个数，分别表示每个地窖中的地雷个数。

第 \(3\) 行至第 \(N+1\) 行表示地窖之间的连接情况：

第 \(3\) 行有 \(n-1\) 个数（\(0\) 或 \(1\)），表示第一个地窖至第 \(2\) 个、第 \(3\) 个 \(\dots\) 第 \(n\) 个地窖有否路径连接。如第 \(3\) 行为 \(11000\cdots 0\)，则表示第 \(1\) 个地窖至第 \(2\) 个地窖有路径，至第 \(3\) 个地窖有路径，至第 \(4\) 个地窖、第 \(5\) 个 \(\dots\) 第 \(n\) 个地窖没有路径。

第 \(4\) 行有 \(n-2\) 个数，表示第二个地窖至第 \(3\) 个、第 \(4\) 个 \(\dots\) 第 \(n\) 个地窖有否路径连接。

……

第 \(n+1\) 行有 \(1\) 个数，表示第 \(n-1\) 个地窖至第 \(n\) 个地窖有否路径连接。（为 \(0\) 表示没有路径，为 \(1\) 表示有路径）。

输出格式

第一行表示挖得最多地雷时的挖地雷的顺序，各地窖序号间以一个空格分隔，不得有多余的空格。

第二行只有一个数，表示能挖到的最多地雷数。

样例 #1

样例输入 #1

1
2
3
4
5
6
5
10 8 4 7 6
1 1 1 0
0 0 0
1 1
1

样例输出 #1

1
2
1 3 4 5
27

提示

【题目来源】

NOIP 1996 提高组第三题

读完题没给我一种dp的感觉，反而是搜索，那就搜索罢

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
int n;
bool f[100][100]; 
int a[1000];
int b[10000];
int path[111000];
int ans[100000];
int cnt;
int cmax;
bool check(int x)
{
	for (int i = 1; i <=n ; i++)
	{
		if (f[x][i]&&!b[i])
		{
			return false;
		}
	}
	return true;
}
//判断函数
void dfs(int x, int stp, int sum)
{
	if (check(x))
	{
		if (cmax<sum)
		{
			cmax = sum;
			cnt = stp;
			for (int i = 1; i <=stp ; i++)
			{
				ans[i] = path[i];
			}
		}
		return;
	}
    //更新答案
	for (int i = 1; i <=n ; i++)
	{
		if (f[x][i]&&!b[i])
		{
			b[i] = 1;
			path[stp + 1] = i;
			dfs(i, stp + 1,  sum + a[i]);
			b[i] = 0;
		}
	}
}
//深搜过程
int main()
{
	cin >> n;
	for (int i = 1; i <=n ; i++)
	{
		cin >> a[i];
	}
	for (int i = 1; i <n ; i++)
	{
		for (int j = i+1; j <=n ; j++)
		{
			cin >> f[i][j];
        }
	}
    //输入
	for (int i = 1; i <=n ; i++)
	{
		b[i] = 1;
		path[1] = i;
		//一个是记录遇见走过
		//一个是记录路径
		dfs(i, 1, a[i]);
		b[i] = 0;
        //恢复现场1
	}
	for (int i = 1; i <=cnt ; i++)
	{
		cout << ans[i] << " ";
	}
	cout << "\n";
	cout << cmax;
	return 0;
}

[SHOI2002] 滑雪

题目描述

Michael 喜欢滑雪。这并不奇怪，因为滑雪的确很刺激。可是为了获得速度，滑的区域必须向下倾斜，而且当你滑到坡底，你不得不再次走上坡或者等待升降机来载你。Michael 想知道在一个区域中最长的滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子： 

1
2
3
4
5
1   2   3   4   5
16  17  18  19  6
15  24  25  20  7
14  23  22  21  8
13  12  11  10  9
一个人可以从某个点滑向上下左右相邻四个点之一，当且仅当高度会减小。在上面的例子中，一条可行的滑坡为 \(24-17-16-1\)（从 \(24\) 开始，在 \(1\) 结束）。当然 \(25\)－\(24\)－\(23\)－\(\ldots\)－\(3\)－\(2\)－\(1\) 更长。事实上，这是最长的一条。

输入格式

输入的第一行为表示区域的二维数组的行数 \(R\) 和列数 \(C\)。下面是 \(R\) 行，每行有 \(C\) 个数，代表高度(两个数字之间用 \(1\) 个空格间隔)。

输出格式

输出区域中最长滑坡的长度。

样例 #1

样例输入 #1

1
2
3
4
5
6
5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9

样例输出 #1

1
25

提示

对于 \(100\%\) 的数据，\(1\leq R,C\leq 100\)。

还是搜索的感觉（）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int dx[4] = { 0,0,1,-1 };
int dy[4] = { 1,-1,0,0 };
int n, m, a[201][201], s[201][201], ans;

int dfs(int x, int y) {
    if (s[x][y])return s[x][y];
    s[x][y] = 1;
    for (int i = 0; i < 4; i++)
    {
        int xx = dx[i] + x;
        int yy = dy[i] + y;//四个方向
        if (xx > 0 && yy > 0 && xx <= n && yy <= m && a[x][y] > a[xx][yy])
        //判断这个方向是否在地图范围内
        //判断这个点是否能滑到
        {
            dfs(xx, yy);
            s[x][y] = max(s[x][y], s[xx][yy] + 1);
        }
    }
    return s[x][y];
}
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> a[i][j];
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            ans = max(ans, dfs(i, j));
cout<<ans;

}

最大食物链计数

题目背景

你知道食物链吗？Delia 生物考试的时候，数食物链条数的题目全都错了，因为她总是重复数了几条或漏掉了几条。于是她来就来求助你，然而你也不会啊！写一个程序来帮帮她吧。

题目描述

给你一个食物网，你要求出这个食物网中最大食物链的数量。

（这里的“最大食物链”，指的是生物学意义上的食物链，即最左端是不会捕食其他生物的生产者，最右端是不会被其他生物捕食的消费者。）

Delia 非常急，所以你只有 \(1\) 秒的时间。

由于这个结果可能过大，你只需要输出总数模上 \(80112002\) 的结果。

输入格式

第一行，两个正整数 \(n、m\)，表示生物种类 \(n\) 和吃与被吃的关系数 \(m\)。

接下来 \(m\) 行，每行两个正整数，表示被吃的生物A和吃A的生物B。

输出格式

一行一个整数，为最大食物链数量模上 \(80112002\) 的结果。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
5 7
1 2
1 3
2 3
3 5
2 5
4 5
3 4

样例输出 #1

1
5

提示

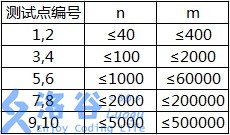
各测试点满足以下约定：

【补充说明】

数据中不会出现环，满足生物学的要求。（感谢 @AKEE ）

拓补排序+dp

dp用来计算食物链的条数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<bits/stdc++.h>
using namespace std;
int n,m,ru[5005],chu[5005],a,b,f[5005],ans;
int mp[5005][5005];
queue<int> q;
int main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		cin>>a>>b;
		mp[a][b]=1;
        //b吃a
		chu[a]++;
		ru[b]++;
	}
    /*
    最佳生产者 的入度一定为 0，而最佳消费者的出度也为 0
    */
	for(int i=1;i<=n;i++){
		if(ru[i]==0) {
			f[i]=1;
			q.push(i);
		}
	}
    //食物链起始，初始化为1
	while(!q.empty()){
		int a=q.front();
		q.pop();
		for(int k=1;k<=n;k++){
			if(mp[a][k]==0)continue;
			f[k]+=f[a];
			f[k]%=80112002;
			ru[k]--;
			if(ru[k]==0)
            {
				if(chu[k]==0)
                {
                    //代表来到了食物链的顶端了
					ans+=f[k];
					ans%=80112002;
				}
				q.push(k);
			}
		}
	}
	cout<<ans; 
}

最大子段和

题目描述

给出一个长度为 \(n\) 的序列 \(a\)，选出其中连续且非空的一段使得这段和最大。

输入格式

第一行是一个整数，表示序列的长度 \(n\)。

第二行有 \(n\) 个整数，第 \(i\) 个整数表示序列的第 \(i\) 个数字 \(a_i\)。

输出格式

输出一行一个整数表示答案。

样例 #1

样例输入 #1

1
2
7
2 -4 3 -1 2 -4 3

样例输出 #1

1
4

提示

样例 1 解释

选取 \([3, 5]\) 子段 \(\{3, -1, 2\}\)，其和为 \(4\)。

数据规模与约定

  • 对于 \(40\%\) 的数据，保证 \(n \leq 2 \times 10^3\)。
  • 对于 \(100\%\) 的数据，保证 \(1 \leq n \leq 2 \times 10^5\)，\(-10^4 \leq a_i \leq 10^4\)。

这个给我一种贪心的感觉（）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <bits/stdc++.h>
using namespace std;
const int N = 1e7;
#define rep(i, a, n) for (int i = a; i <= n; i++)
using ll=long long;
int a;
int main()
{
int n;
cin>>n;
int f=0;
int ans=-999999999;
rep(i,1,n)
{
cin>>a;
f=max(f+a,a);
//如果加上比这个值本身还小，加他干什么呢
ans=max(f,ans);
//维护作用
}
cout<<ans;
}

5 倍经验日

题目背景

现在乐斗有活动了！每打一个人可以获得 5 倍经验！absi2011 却无奈的看着那一些比他等级高的好友，想着能否把他们干掉。干掉能拿不少经验的。

题目描述

现在 absi2011 拿出了 \(x\) 个迷你装药物（嗑药打人可耻…），准备开始与那些人打了。

由于迷你装药物每个只能用一次，所以 absi2011 要谨慎的使用这些药。悲剧的是，用药量没达到最少打败该人所需的属性药药量，则打这个人必输。例如他用 \(2\) 个药去打别人，别人却表明 \(3\) 个药才能打过，那么相当于你输了并且这两个属性药浪费了。

现在有 \(n\) 个好友，给定失败时可获得的经验、胜利时可获得的经验，打败他至少需要的药量。

要求求出最大经验 \(s\)，输出 \(5s\)。

输入格式

第一行两个数，\(n\) 和 \(x\)。

后面 \(n\) 行每行三个数，分别表示失败时获得的经验 \(\mathit{lose}_i\)，胜利时获得的经验 \(\mathit{win}_i\) 和打过要至少使用的药数量 \(\mathit{use}_i\)。

输出格式

一个整数，最多获得的经验的五倍。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
6 8
21 52 1
21 70 5
21 48 2
14 38 3
14 36 1
14 36 2

样例输出 #1

1
1060

提示

【Hint】

五倍经验活动的时候，absi2011 总是吃体力药水而不是这种属性药。

【数据范围】

  • 对于 \(10\%\) 的数据，保证 \(x=0\)。
  • 对于 \(30\%\) 的数据，保证 \(0\le n\le 10\)，\(0\le x\le 20\)。
  • 对于 \(60\%\) 的数据，保证 \(0\le n,x\le 100\)， \(10<lose_i,win_i\le 100\)，\(0\le use_i\le 5\)。
  • 对于 \(100\%\) 的数据，保证 \(0\le n,x\le 10^3\)，\(0<lose_i\le win_i\le 10^6\)，\(0\le use_i\le 10^3\)。

【题目来源】

fight.pet.qq.com

absi2011 授权题目

隐藏的小贪心

打不过，我用药还打不过，我用干嘛？

所以说，打得过的可以用药也可以并不用药

但打不过的一定不用药

这样分析就行

和01背包也是相差无几

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
int n, x;
int f[100000];
int w[100000];
int dp[1000][111];
int y[10000];
//表示能够打败第i人所剩下j药剂时候的经验值
int main()
{
	cin >> n >> x;
	for (int i = 1; i <= n; i++)
	{
		cin >> f[i] >> w[i] >> y[i];
		
	}

	for (int i = 1; i <=n ; i++)
	{
		for (int j = x; j >=0; j--)
		{
			if (j>=y[i])
			{
				dp[i][j] = max(dp[i - 1][j - y[i]] + w[i], dp[i - 1][j] + f[i]);


			}
			else
			{
				dp[i][j] = dp[i - 1][j] + f[i];
			}


		}

	}

	cout << dp[n][x]*5ll;


	return 0;
}

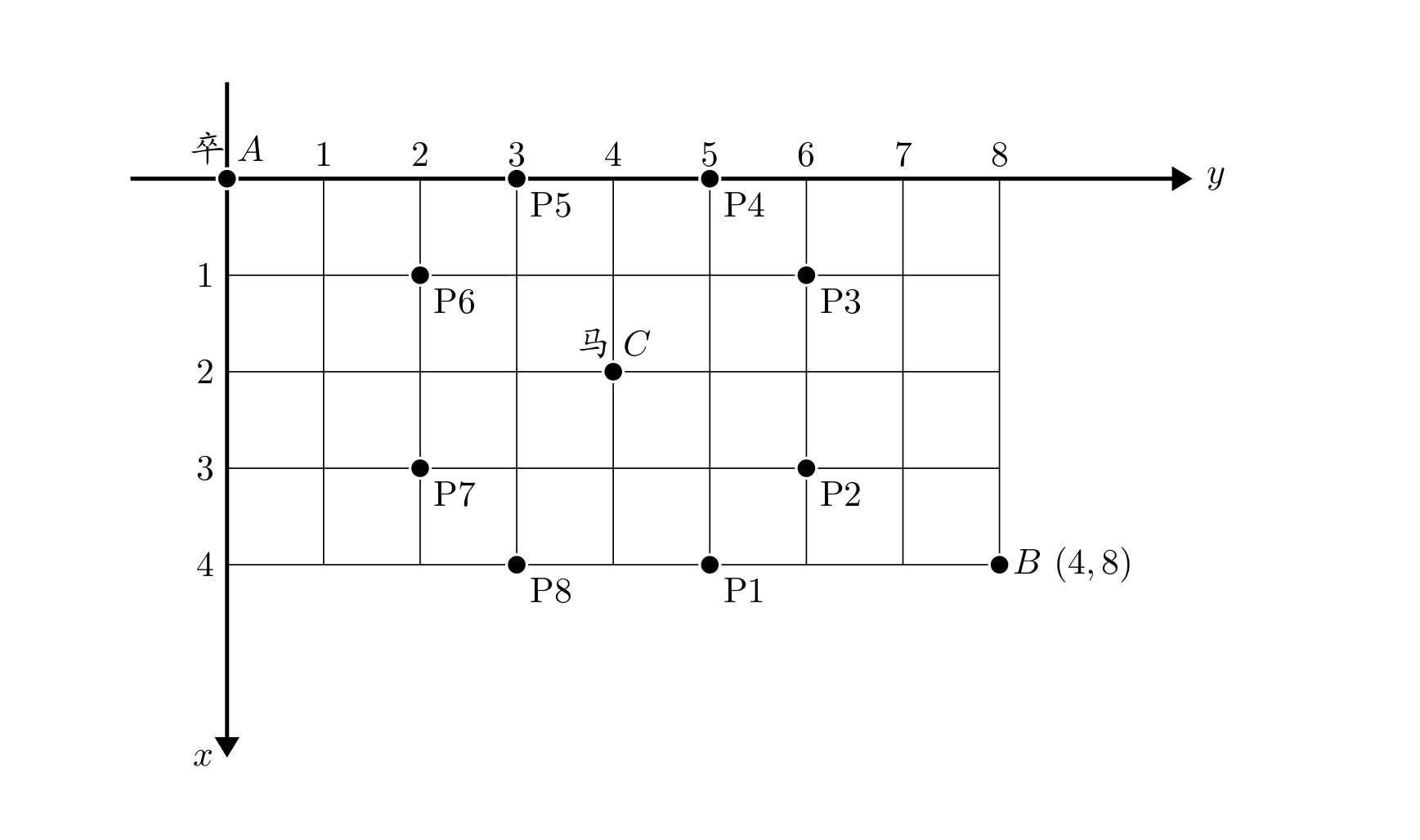
[NOIP2002 普及组] 过河卒

题目描述

棋盘上 \(A\) 点有一个过河卒，需要走到目标 \(B\) 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 \(C\) 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，\(A\) 点 \((0, 0)\)、\(B\) 点 \((n, m)\)，同样马的位置坐标是需要给出的。

现在要求你计算出卒从 \(A\) 点能够到达 \(B\) 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 \(B\) 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

样例 #1

样例输入 #1

1
6 6 3 3

样例输出 #1

1
6

提示

对于 \(100 \%\) 的数据，\(1 \le n, m \le 20\)，\(0 \le\) 马的坐标 \(\le 20\)。

【题目来源】

NOIP 2002 普及组第四题

一道对于几个月前的我焦头烂额，彻夜难眠的水题（）

实际上只需要进行控制点的跳过，然后进行递推就可以了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
#include<cstdio>
using namespace std;
#define N 22
long long a[N][N];
int crt[N][N];
int d[9][2] = { {0,0},{-2,1},{-2,-1},{2,1},{2,-1},{1,2},{1,-2},{-1,-2},{-1,2} };
int main()
{
	int n, m, hx, hy;
	cin >> n >> m >> hx >> hy;
	for (int i = 0; i < 9	; i++)
	{
		int tempx = hx +d[i][0];
		int tempy = hy + d[i][1];
		if (tempx>=0&&tempx<=n&&tempy>=0&&tempy<=m)
		{
			crt[tempx][tempy] = 1;
		}
		//控制点，用来跳过的
	}
	a[0][0] = 1 - crt[0][0];
    //由于这是初始点，还是特判一下，方便后面递推
	for (int i = 0; i <=n ; i++)
	{
		for (int j = 0; j <=m ; j++)
		{
			if (crt[i][j])
			{
				continue;
                //控制点就跳过
			}
			if (i!=0)
			{
				a[i][j] += a[i - 1][j];
			}
			if (j!=0)
			{
				a[i][j] += a[i][j - 1];
			}
            //避免出现数组越界
		}
	}
	cout << a[n][m];
	return 0;
}

[NOIP2001 普及组] 装箱问题

题目描述

有一个箱子容量为 \(V\)，同时有 \(n\) 个物品，每个物品有一个体积。

现在从 \(n\) 个物品中，任取若干个装入箱内（也可以不取），使箱子的剩余空间最小。输出这个最小值。

输入格式

第一行共一个整数 \(V\)，表示箱子容量。

第二行共一个整数 \(n\)，表示物品总数。

接下来 \(n\) 行，每行有一个正整数，表示第 \(i\) 个物品的体积。

输出格式

  • 共一行一个整数，表示箱子最小剩余空间。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
24
6
8
3
12
7
9
7

样例输出 #1

1
0

提示

对于 \(100\%\) 数据，满足 \(0<n \le 30\)，\(1 \le V \le 20000\)。

【题目来源】

NOIP 2001 普及组第四题

01背包裸题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
int dp[100000000];
int a[100000000];
int main()
	{
	int v, n;
	cin >> v >> n;
	for (int i = 1; i <=n ; i++)
	{
		cin >> a[i];
	}
	
	for (int i = 1; i <=n ; i++)
	{
		for ( int j = v;  j >=0;  j--)
		{

			if (j>=a[i])
			{
				dp[j] = max(dp[j - 1], dp[j - a[i]] + a[i]);
			}
			

		}


	}

	cout << v - dp[v];


	}

疯狂的采药

题目背景

此题为纪念 LiYuxiang 而生。

题目描述

LiYuxiang 是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同种类的草药，采每一种都需要一些时间，每一种也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是 LiYuxiang，你能完成这个任务吗？

此题和原题的不同点：

\(1\). 每种草药可以无限制地疯狂采摘。

\(2\). 药的种类眼花缭乱，采药时间好长好长啊！师傅等得菊花都谢了！

输入格式

输入第一行有两个整数，分别代表总共能够用来采药的时间 \(t\) 和代表山洞里的草药的数目 \(m\)。

第 \(2\) 到第 \((m + 1)\) 行，每行两个整数，第 \((i + 1)\) 行的整数 \(a_i, b_i\) 分别表示采摘第 \(i\) 种草药的时间和该草药的价值。

输出格式

输出一行，这一行只包含一个整数，表示在规定的时间内，可以采到的草药的最大总价值。

样例 #1

样例输入 #1

1
2
3
4
70 3
71 100
69 1
1 2

样例输出 #1

1
140

提示

数据规模与约定

  • 对于 \(30\%\) 的数据，保证 \(m \le 10^3\) 。
  • 对于 \(100\%\) 的数据，保证 \(1 \leq m \le 10^4\)，\(1 \leq t \leq 10^7\)，且 \(1 \leq m \times t \leq 10^7\)，\(1 \leq a_i, b_i \leq 10^4\)。

完全背包，因此可以进行采药的正推版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//P1616 疯狂的采药
#include<iostream>
#include<algorithm>
using namespace std;
long long a[10000000];
long long b[10000000];
long long dp[100000000];
//表示采摘第i住草药花费的j时间有的价值
int main()
{
	long long t, m;
	cin >> t >> m;
	for (int i = 1; i <=m; i++)
	{
		cin >> a[i] >> b[i];
	}

	for (int i = 1; i <=m ; i++)
	{
		for (int j = a[i]; j <=t; j++)
		{
			dp[j] = max(dp[j], dp[j - a[i]] + b[i]);


		}


	}
	

	cout << dp[t]*1ll;


}

小A点菜

题目背景

uim 神犇拿到了 uoi 的 ra（镭牌）后，立刻拉着基友小 A 到了一家……餐馆，很低端的那种。

uim 指着墙上的价目表（太低级了没有菜单），说：“随便点”。

题目描述

不过 uim 由于买了一些书，口袋里只剩 \(M\) 元 \((M \le 10000)\)。

餐馆虽低端，但是菜品种类不少，有 \(N\) 种 \((N \le 100)\)，第 \(i\) 种卖 \(a_i\) 元 \((a_i \le 1000)\)。由于是很低端的餐馆，所以每种菜只有一份。

小 A 奉行“不把钱吃光不罢休”，所以他点单一定刚好把 uim 身上所有钱花完。他想知道有多少种点菜方法。

由于小 A 肚子太饿，所以最多只能等待 \(1\) 秒。

输入格式

第一行是两个数字，表示 \(N\) 和 \(M\)。

第二行起 \(N\) 个正数 \(a_i\)（可以有相同的数字，每个数字均在 \(1000\) 以内）。

输出格式

一个正整数，表示点菜方案数，保证答案的范围在 int 之内。

样例 #1

样例输入 #1

1
2
4 4
1 1 2 2

样例输出 #1

1
3

提示

2020.8.29，增添一组 hack 数据 by @yummy

方案数可以考虑dp

（1）if(j==第i道菜的价格)f[i] [j]=f[i-1] [j]+1;

（2）if(j>第i道菜的价格) f[i] [j]=f[i-1] [j]+f[i-1] [j-第i道菜的价格];

（3）if(j<第i道菜的价格) f[i] [j]=f[i-1] [j];

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int a[1010], f[1010][100010] ;
int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; ++i)cin >> a[i];
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m; ++j)
        {
            if (j == a[i])f[i][j] = f[i - 1][j] + 1;
            if (j > a[i]) f[i][j] = f[i - 1][j] + f[i - 1][j - a[i]];
            if (j < a[i]) f[i][j] = f[i - 1][j];
        }
    cout<< f[n][m];

}

[NOIP2012 普及组] 摆花

题目描述

小明的花店新开张，为了吸引顾客，他想在花店的门口摆上一排花，共 \(m\) 盆。通过调查顾客的喜好，小明列出了顾客最喜欢的 \(n\) 种花，从 \(1\) 到 \(n\) 标号。为了在门口展出更多种花，规定第 \(i\) 种花不能超过 \(a_i\) 盆，摆花时同一种花放在一起，且不同种类的花需按标号的从小到大的顺序依次摆列。

试编程计算，一共有多少种不同的摆花方案。

输入格式

第一行包含两个正整数 \(n\) 和 \(m\)，中间用一个空格隔开。

第二行有 \(n\) 个整数，每两个整数之间用一个空格隔开，依次表示 \(a_1,a_2, \cdots ,a_n\)。

输出格式

一个整数，表示有多少种方案。注意：因为方案数可能很多，请输出方案数对 \(10^6+7\) 取模的结果。

样例 #1

样例输入 #1

1
2
2 4
3 2

样例输出 #1

1
2

提示

【数据范围】

对于 \(20\%\) 数据，有 \(0<n \le 8,0<m \le 8,0 \le a_i \le 8\)。

对于 \(50\%\) 数据，有 \(0<n \le 20,0<m \le 20,0 \le a_i \le 20\)。

对于 \(100\%\) 数据，有 \(0<n \le 100,0<m \le 100,0 \le a_i \le 100\)。

NOIP 2012 普及组 第三题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
int a[100000];
int dp[10000000];
int main()
{
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
	}
	dp[0] = 1;
	for (int i = 1; i <=n; i++)
	{
		for (int j = m; j>=0  ; j--)
		{
			for (int k =1 ; k <=min(a[i],j) ; k++)
			{
				dp[j] = (dp[j] + dp[j - k]) % 1000007;

			}
		}
	}
	//dp[i][j]的含义究竟是什么呢，就是摆第i种花的时候所能摆出多少盆花
//dp[i][j]可以从什么推导过来呢，假如我们这盆花不摆出来就是原样
	//如果我们要摆我们就要摆多少盆呢，那我们是不是需要来个循环，枚举他的盆数，由于是方案我们要相加
	//这是二维dp
	cout << dp[m];
}

[TJOI2007] 线段

题目描述

在一个 \(n \times n\) 的平面上，在每一行中有一条线段，第 \(i\) 行的线段的左端点是\((i, L_{i})\)，右端点是\((i, R_{i})\)。

你从 \((1,1)\) 点出发，要求沿途走过所有的线段，最终到达 \((n,n)\) 点，且所走的路程长度要尽量短。

更具体一些说，你在任何时候只能选择向下走一步（行数增加 \(1\)）、向左走一步（列数减少 \(1\)）或是向右走一步（列数增加 \(1\)）。当然，由于你不能向上行走，因此在从任何一行向下走到另一行的时候，你必须保证已经走完本行的那条线段。

输入格式

第一行有一个整数 \(n\)。

以下 \(n\) 行，在第 \(i\) 行（总第 \((i+1)\) 行）的两个整数表示 \(L_i\) 和 \(R_i\)。

输出格式

仅包含一个整数，你选择的最短路程的长度。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
6
2 6
3 4
1 3
1 2
3 6
4 5

样例输出 #1

1
24

提示

我们选择的路线是

1
2
3
4
5
6
(1, 1) (1, 6)
(2, 6) (2, 3)
(3, 3) (3, 1)
(4, 1) (4, 2)
(5, 2) (5, 6)
(6, 6) (6, 4) (6, 6)

不难计算得到，路程的总长度是 \(24\)。

对于 \(100\%\) 的数据中，\(n \le 2 \times 10^4\)，\(1 \le L_i \le R_i \le n\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<iostream>
#include<algorithm>
#include<string>
#include<math.h>
using namespace std;
int l[600000];
int r[60000];
int f[60000][2];
int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <=n ; i++)
	{
		cin >> l[i] >> r[i];
	}
	f[1][1] = r[1] - 1;
	f[1][0] = r[1] - 1 + r[1] - l[1];
//由于必须走完一整条线段
	for (int i = 2; i <=n ; i++)
	{
		f[i][1] = min(f[i - 1][0] + r[i] - l[i] + abs(l[i] - l[i - 1])+1, f[i - 1][1] + r[i] - l[i] + abs(r[i - 1] - l[i])+1);
		f[i][0] = min(f[i - 1][0] + r[i] - l[i] + abs(r[i] - l[i - 1])+1, f[i - 1][1] + r[i] - l[i] + abs(r[i - 1] - r[i])+1) ;
	}
	cout << min(f[n][1]+n-r[n], f[n][0]+n-l[n]);
}

f[i][0]表示走完第i行且停在第i行的左端点最少用的步数

f[i][1]同理，停在右端点的最少步数。



[NOIP2006 提高组] 金明的预算方案

题目描述

金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过 \(n\) 元钱就行”。今天一早，金明就开始做预算了，他把想买的物品分为两类：主件与附件，附件是从属于某个主件的，下表就是一些主件与附件的例子：

主件 附件
电脑 打印机，扫描仪
书柜 图书
书桌 台灯，文具
工作椅 无

如果要买归类为附件的物品，必须先买该附件所属的主件。每个主件可以有 \(0\) 个、\(1\) 个或 \(2\) 个附件。每个附件对应一个主件，附件不再有从属于自己的附件。金明想买的东西很多，肯定会超过妈妈限定的 \(n\) 元。于是，他把每件物品规定了一个重要度，分为 \(5\) 等：用整数 \(1 \sim 5\) 表示，第 \(5\) 等最重要。他还从因特网上查到了每件物品的价格（都是 \(10\) 元的整数倍）。他希望在不超过 \(n\) 元的前提下，使每件物品的价格与重要度的乘积的总和最大。

设第 \(j\) 件物品的价格为 \(v_j\)，重要度为\(w_j\)，共选中了 \(k\) 件物品，编号依次为 \(j_1,j_2,\dots,j_k\)，则所求的总和为：

\(v_{j_1} \times w_{j_1}+v_{j_2} \times w_{j_2}+ \dots +v_{j_k} \times w_{j_k}\)。

请你帮助金明设计一个满足要求的购物单。

输入格式

第一行有两个整数，分别表示总钱数 \(n\) 和希望购买的物品个数 \(m\)。

第 \(2\) 到第 \((m + 1)\) 行，每行三个整数，第 \((i + 1)\) 行的整数 \(v_i\)，\(p_i\)，\(q_i\) 分别表示第 \(i\) 件物品的价格、重要度以及它对应的的主件。如果 \(q_i=0\)，表示该物品本身是主件。

输出格式

输出一行一个整数表示答案。

样例 #1

样例输入 #1

1
2
3
4
5
6
1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0

样例输出 #1

1
2200

提示

数据规模与约定

对于全部的测试点，保证 \(1 \leq n \leq 3.2 \times 10^4\)，\(1 \leq m \leq 60\)，\(0 \leq v_i \leq 10^4\)，\(1 \leq p_i \leq 5\)，\(0 \leq q_i \leq m\)，答案不超过 \(2 \times 10^5\)。

NOIP 2006 提高组 第二题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
int v, p, q;
const int N = 32005;
int w[N];
int c[N];
int _w[N][6];
int _c[N][6];
int dp[N];
int main()
{
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <=m ; i++)
	{
		cin >> v >> p >> q;
		if (!q)
		{
			w[i] = v;
			c[i] = v * p;

		}
		else
		{
			_w[q][0]++;
            //记录个数
			_w[q][_w[q][0]] = v;
			_c[q][_w[q][0]] = v * p;

			
		}
	}
	for (int i = 1; i <=m ; i++)
	{
		for (int j = n; j >=w[i]; j--)
		{
			
			
            /*
            这个题的决策是五个，分别是：

1.不选，然后去考虑下一个

2.选且只选这个主件

3.选这个主件，并且选附件1

4.选这个主件，并且选附件2

5.选这个主件，并且选附件1和附件2.
            */
				dp[j] = max(dp[j], dp[j - w[i]] + c[i]);
		
			if (j>=w[i]+_w[i][1])
			{
				dp[j] = max(dp[j], dp[j - w[i] - _w[i][1]]+ c[i] + _c[i][1]);
			}
			if (j>=w[i]+_w[i][2])
			{
				dp[j] = max(dp[j], dp[j - w[i] - _w[i][2]] + c[i] + _c[i][2]);

			}
			if (j>=w[i]+_w[i][1]+_w[i][2])
			{
				dp[j] = max(dp[j], dp[j - w[i] - _w[i][1] - _w[i][2]] + c[i] + _c[i][1] + _c[i][2]);
			}
		}



	}
	cout << dp[n]<<endl;
	return 0;
}

kkksc03考前临时抱佛脚

题目背景

kkksc03 的大学生活非常的颓废，平时根本不学习。但是，临近期末考试，他必须要开始抱佛脚，以求不挂科。

题目描述

这次期末考试，kkksc03 需要考 \(4\) 科。因此要开始刷习题集，每科都有一个习题集，分别有 \(s_1,s_2,s_3,s_4\) 道题目，完成每道题目需要一些时间，可能不等（\(A_1,A_2,\ldots,A_{s_1}\)，\(B_1,B_2,\ldots,B_{s_2}\)，\(C_1,C_2,\ldots,C_{s_3}\)，\(D_1,D_2,\ldots,D_{s_4}\)）。

kkksc03 有一个能力，他的左右两个大脑可以同时计算 \(2\) 道不同的题目，但是仅限于同一科。因此，kkksc03 必须一科一科的复习。

由于 kkksc03 还急着去处理洛谷的 bug，因此他希望尽快把事情做完，所以他希望知道能够完成复习的最短时间。

输入格式

本题包含 \(5\) 行数据：第 \(1\) 行，为四个正整数 \(s_1,s_2,s_3,s_4\)。

第 \(2\) 行，为 \(A_1,A_2,\ldots,A_{s_1}\) 共 \(s_1\) 个数，表示第一科习题集每道题目所消耗的时间。

第 \(3\) 行，为 \(B_1,B_2,\ldots,B_{s_2}\) 共 \(s_2\) 个数。

第 \(4\) 行，为 \(C_1,C_2,\ldots,C_{s_3}\) 共 \(s_3\) 个数。

第 \(5\) 行，为 \(D_1,D_2,\ldots,D_{s_4}\) 共 \(s_4\) 个数，意思均同上。

输出格式

输出一行,为复习完毕最短时间。

样例 #1

样例输入 #1

1
2
3
4
5
1 2 1 3		
5
4 3
6
2 4 3

样例输出 #1

1
20

提示

\(1\leq s_1,s_2,s_3,s_4\leq 20\)。

\(1\leq A_1,A_2,\ldots,A_{s_1},B_1,B_2,\ldots,B_{s_2},C_1,C_2,\ldots,C_{s_3},D_1,D_2,\ldots,D_{s_4}\leq60\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
//四份01背包
//每一科都是一样的复习方式
//所以相当于有4组数据
//因此可以只分析一组
//而一组我们可以分析理想情况，就是其中一部分的和等于总和的一半
//那么问题很明朗
//就是用一部分题目去尽量装满总和的一半这个背包
//然后+上总和减去的部分即可
#include<bits/stdc++.h>
using namespace std;
int len[4];
int sub[30];
int f[21][1201];
int main(){
    for(int i=0;i<4;i++) cin>>len[i];
    int tot=0;
    for(int i=0;i<4;i++){
        int v=0;
        for(int j=1;j<=len[i];j++) cin>>sub[j],v+=sub[j];
        sort(sub,sub+len[i]);
        int t1=0;
        for(int j=1;j<=len[i];j++)
            for(int k=0;k<=v/2;k++){
                f[j][k]=f[j-1][k];
                if(k>=sub[j])f[j][k]=max(f[j][k],f[j-1][k-sub[j]]+sub[j]);
                t1=max(f[j][k],t1);
            }
        tot+=max(t1,v-t1);
    }
    cout<<tot;
}