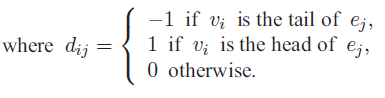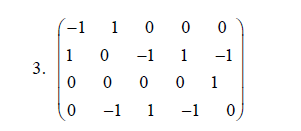华南理工大学期末考试《离散数学》试卷A

一、填空题

1. 将公式 $\exists x P(x) \to \exists x Q(x, y)$ 转为前束范式

问题: 求公式 $\exists x P(x) \to \exists x Q(x, y)$ 的前束范式。
答案: $\forall x \exists z (P(x) \to Q(z, y))$。
解释:

  1. 将蕴含式 $A \to B$ 转换为 $\neg A \lor B$，公式变为 $\neg (\exists x P(x)) \lor (\exists x Q(x, y))$。
  2. 使用量词的否定规则，$\neg (\exists x P(x))$ 转为 $\forall x \neg P(x)$，因此公式变为 $(\forall x \neg P(x)) \lor (\exists x Q(x, y))$。
  3. 根据等价变换规则，将公式标准化：$\forall x \exists z (P(x) \to Q(z, y))$。

2. 集合运算问题 $B - A$

问题: 设集合 $A = \{a, b, \{a,b\}, \emptyset\}$, $B = \{\{a,b\}, \emptyset\}$，求 $B - A$。
答案: $\emptyset$。
解释:

  1. $B - A$ 的定义是 $B$ 中属于 $B$ 但不属于 $A$ 的元素集合。
  2. 逐个检查 $B$ 中的元素：
    • $\{a, b\}$ 在 $A$ 中，故不计入结果。
    • $\emptyset$ 在 $A$ 中，故不计入结果。
  3. 因此，$B - A = \emptyset$。

3. 命题逻辑问题

问题: 设 $p = 0, q = 0, r = 1, s = 1$，求命题 $\neg (s \lor (q \to (r \lor \neg p))) \to (r \land \neg p)$ 的真值。
答案: 1 (真)。
解释:

  1. 化简公式：
    • $q \to (r \lor \neg p)$ 等价于 $\neg q \lor (r \lor \neg p)$。
    • 代入 $q = 0, r = 1, p = 0$，得 $\neg q \lor (r \lor \neg p) = 1 \lor (1 \lor 1) = 1$。
    • $s \lor (q \to (r \lor \neg p)) = 1 \lor 1 = 1$。
    • $\neg (s \lor (q \to (r \lor \neg p))) = \neg 1 = 0$。
  2. 分析右侧公式 $r \land \neg p$：
    • 代入 $r = 1, p = 0$，得 $1 \land 1 = 1$。
  3. 分析蕴含式：$\neg (s \lor (q \to (r \lor \neg p))) \to (r \land \neg p)$：
    • 等价于 $0 \to 1 = 1$。
  4. 因此，命题的真值为 $1$ (真)。

4. 二元关系 $R$ 的性质分析

问题: 设 $R$ 是在正整数集合 $\mathbb{Z}^+$ 上定义的二元关系：
$ R = \{(x, y) \mid x, y \in \mathbb{Z}^+ \text{ 且 } x + y = 10\} $
求 $R$ 的有序对个数，并判断其具有的性质（自反性、对称性、传递性、反自反性、反对称性）。
答案:

  • $R$ 一共有 9 个有序对。
  • $R$ 的性质为：对称性。

解释:

  1. 列出满足 $x + y = 10$ 的所有正整数有序对：
    $
    R = \{(1, 9), (2, 8), (3, 7), (4, 6), (5, 5), (6, 4), (7, 3), (8, 2), (9, 1)\}
    $
    共 9 个有序对。

  2. 检查性质：

    • 自反性: $R$ 无自反性。
    • 对称性: 若 $(x, y) \in R$，则 $x + y = 10$，显然 $(y, x) \in R$。故 $R$ 有对称性。
    • 传递性: 若 $(x, y) \in R$ 且 $(y, z) \in R$，则需满足 $(x, z) \in R$。例如：
      • $(1, 9) \in R$ 且 $(9, 1) \in R$，但 $(1, 1) \notin R$，不满足传递性。
    • 反自反性: $R$ 无反自反性。
    • 反对称性: 若 $(x, y) \in R$ 且 $(y, x) \in R$，需满足 $x = y$。例如 $(1, 9), (9, 1) \in R$，但 $1 \neq 9$。故 $R$ 无反对称性。

5. 公式中自由变元与约束变元

问题: 对公式 $\forall x (P(x) \to Q(x, y)) \to S(x)$，判断自由变元与约束变元。
答案:

  • 自由变元：$y$ 与 $S(x)$ 中的 $x$。
  • 约束变元：$P(x)$ 中的 $x$，以及 $Q(x, y)$ 中的 $x$。

解释:

  1. 自由变元:

    • $y$ 在 $Q(x, y)$ 中未被量词约束，因此 $y$ 是自由变元。
    • $S(x)$ 中的 $x$ 未被量词约束，因此也是自由变元。

  2. 约束变元:

    • $\forall x$ 将 $P(x)$ 和 $Q(x, y)$ 中的 $x$ 绑定为约束变元，因此 $x$ 是约束变元。

最终，公式的自由变元为 $y$ 和 $S(x)$ 中的 $x$；约束变元为 $\forall x$ 中的 $x$。

6. 命题的逻辑表达式

问题: 设有命题 $T(x)$: $x$ 是火车, $C(x)$: $x$ 是汽车, $Q(x, y)$: $x$ 跑得比 $y$ 快。表达“有的汽车比一些火车跑得快”的逻辑表达式。
答案:
$
\exists x (C(x) \land \exists y (T(y) \land Q(x, y)))
$

解释:

  • 命题分析:
    • “有的汽车”对应存在量词 $\exists x$，且满足 $C(x)$。
    • “比一些火车跑得快”表示存在某个 $y$，它是火车（$T(y)$），且 $x$ 比 $y$ 快（$Q(x, y)$）。
  • 综合起来，表示有某个 $x$ 是汽车，且存在 $y$ 是火车，使得 $x$ 比 $y$ 快。
  • 逻辑表达式为：
    $
    \exists x (C(x) \land \exists y (T(y) \land Q(x, y)))
    $

7. 无向图是树的条件

问题: 设 $G$ 是 $n$ 阶 $m$ 条边的无向图，若 $G$ 连通且 $G$ 是无向树，则 $m =$。
答案:
$
m = n - 1
$

解释:

  1. 树的定义:

    • 树是一个无向图，具有以下性质：
      • 连通。
      • 无环。

  2. 树的边数性质:

    • 在 $n$ 个顶点的连通无向图中，形成一棵树所需的最小边数为 $m = n - 1$。
    • 若边数少于 $n - 1$，图不连通；若多于 $n - 1$，会形成环，违反树的定义。

  3. 总结:
    若无向图 $G$ 连通且为树，则其边数满足 $m = n - 1$。

8. 复合函数的计算

集合 $X = \{1, 2, 3\}$，函数
$
f = \{ \langle 1, 2 \rangle, \langle 2, 3 \rangle, \langle 3, 1 \rangle \}, \quad g = \{ \langle 1, 2 \rangle, \langle 2, 3 \rangle, \langle 3, 3 \rangle \}.
$

计算 $f^{-1}$

反函数 $f^{-1}$ 将 $f$ 中的有序对反转：
$
f^{-1} = \{ \langle 2, 1 \rangle, \langle 3, 2 \rangle, \langle 1, 3 \rangle \}.
$

计算 $f^{-1} \circ g$

根据定义：
$
f^{-1} \circ g = \{ \langle x, z \rangle \mid \exists y, \langle x, y \rangle \in g \land \langle y, z \rangle \in f^{-1} \}.
$

对每个 $x \in X$ 计算：

  1. $x = 1$:

    • $g(1) = 2$，查找 $f^{-1}(2)$: $\langle 2, 1 \rangle$。
    • 因此 $\langle 1, 1 \rangle \in f^{-1} \circ g$。

  2. $x = 2$:

    • $g(2) = 3$，查找 $f^{-1}(3)$: $\langle 3, 2 \rangle$。
    • 因此 $\langle 2, 2 \rangle \in f^{-1} \circ g$。

  3. $x = 3$:

    • $g(3) = 3$，查找 $f^{-1}(3)$: $\langle 3, 2 \rangle$。
    • 因此 $\langle 3, 2 \rangle \in f^{-1} \circ g$。

最终结果:
$
f^{-1} \circ g = \{ \langle 1, 1 \rangle, \langle 2, 2 \rangle, \langle 3, 2 \rangle \}.
$

计算 $g \circ f$

根据定义：
$
g \circ f = \{ \langle x, z \rangle \mid \exists y, \langle x, y \rangle \in f \land \langle y, z \rangle \in g \}.
$

对每个 $x \in X$ 计算：

  1. $x = 1$:

    • $f(1) = 2$，查找 $g(2)$: $\langle 2, 3 \rangle$。
    • 因此 $\langle 1, 3 \rangle \in g \circ f$。

  2. $x = 2$:

    • $f(2) = 3$，查找 $g(3)$: $\langle 3, 3 \rangle$。
    • 因此 $\langle 2, 3 \rangle \in g \circ f$。

  3. $x = 3$:

    • $f(3) = 1$，查找 $g(1)$: $\langle 1, 2 \rangle$。
    • 因此 $\langle 3, 2 \rangle \in g \circ f$。

最终结果:
$
g \circ f = \{ \langle 1, 3 \rangle, \langle 2, 3 \rangle, \langle 3, 2 \rangle \}.
$

最终答案

$
f^{-1} \circ g = \{ \langle 1, 1 \rangle, \langle 2, 2 \rangle, \langle 3, 2 \rangle \}, \quad g \circ f = \{ \langle 1, 3 \rangle, \langle 2, 3 \rangle, \langle 3, 2 \rangle \}.
$

9. 命题的分类

问题:

  • 不能再分解的命题称为 _。
  • 至少包含一个联结词的命题称为 _。

答案:
$
\text{原子命题 (atomic proposition), 复合命题 (compound proposition)}。
$

解释:

  1. 原子命题:

    • 指无法分解成更简单命题的基本命题。
    • 例如：“今天下雨”是原子命题。

  2. 复合命题:

    • 指至少包含一个联结词（如 $\land, \lor, \neg, \rightarrow$）的命题。
    • 例如：“今天下雨且明天晴天”是复合命题。

10. 连通无向图 $ G $ 含有欧拉回路的充分必要条件

问题:
连通无向图 $ G $ 含有欧拉回路的充分必要条件是什么？

答案:
图中无奇数度顶点。

解释:

  • 欧拉回路的定义：欧拉回路是经过图中每条边恰好一次的封闭路径。
  • 充分性:
    如果图中所有顶点的度数均为偶数，则可以从任意顶点出发，一直回到起点并经过每条边一次，这构成欧拉回路。
  • 必要性:
    如果图含有奇数度顶点，则无法完成欧拉回路，因为每次进入一个顶点需要从另一个边离开。若某顶点的度数为奇数，无法满足这一条件。

因此，连通且无奇数度顶点是 $ G $ 含有欧拉回路的充分必要条件。

11. 幂集和元素数量

问题:
设集合 $ A = \{\emptyset, \{a\}\} $，求幂集 $ P(A) $ 和 $ |P(A)| $。

答案:
$
P(A) = \{\emptyset, \{\emptyset\}, \{\{a\}\}, \{\emptyset, \{a\}\}\}, \quad |P(A)| = 4。
$

解释:

  1. 幂集定义：一个集合 $ A $ 的幂集 $ P(A) $ 是包含 $ A $ 的所有子集的集合。

    • $ A = \{\emptyset, \{a\}\} $。
    • $ A $ 的子集包括：
      • 空集 $\emptyset$，
      • 单元素子集 $\{\emptyset\}$ 和 $\{\{a\}\}$，
      • 整个集合本身 $\{\emptyset, \{a\}\}$。
    • 因此：
      $
      P(A) = \{\emptyset, \{\emptyset\}, \{\{a\}\}, \{\emptyset, \{a\}\}\}。
      $

  2. 幂集的大小：

    • 若集合 $ A $ 的元素个数为 $ n $，则幂集的大小为 $ |P(A)| = 2^n $。
    • 这里 $ n = 2 $，所以 $ |P(A)| = 2^2 = 4 $。

12. 图的子图与生成子图

问题:
设 $ G = (V, E), G’ = (V’, E’) $ 为两个图（同为无向图或有向图），若 $ E’ \subseteq E $ 且 ___，则称 $ G’ $ 是 $ G $ 的子图；若 $ E’ \subseteq E $ 且 ___，则称 $ G’ $ 是 $ G $ 的生成子图。

答案:

  1. $ G’ $ 是 $ G $ 的子图：$ V’ \subseteq V $。
  2. $ G’ $ 是 $ G $ 的生成子图：$ V’ = V $。

解释:

  1. 子图定义:

    • 子图要求边集 $ E’ $ 是 $ G $ 边集 $ E $ 的子集，点集 $ V’ $ 是 $ G $ 点集 $ V $ 的子集。
    • 形式化定义：
      $
      G’ = (V’, E’), \quad E’ \subseteq E, \quad V’ \subseteq V。
      $

  2. 生成子图定义:

    • 生成子图要求 $ G’ $ 的点集 $ V’ $ 与 $ G $ 的点集 $ V $ 完全一致，即 $ V’ = V $，但允许边集 $ E’ $ 是 $ E $ 的子集。
    • 形式化定义：
      $
      G’ = (V, E’), \quad E’ \subseteq E。
      $

选择题

问题1：

判断命题公式是否为重言式

问题:
以下命题公式中，哪个是重言式？

  • $ A. (p \lor \neg p) \to q $
  • $ B. p \to (p \lor q) $
  • $ C. q \land \neg q $
  • $ D. (p \to \neg p) \to \neg q $

答案: B

问题2：

问题:
以下语句中，哪个是命题？

  • $ A. $ 你好吗？
  • $ B. $ 人有 6 指。
  • $ C. $ 我所说的是假的。
  • $ D. $ 明天是晴天。

答案: D

问题3：

问题:
设 $ D = (V, E) $ 为有向图，$ V = \{a, b, c, d, e, f\}, E = \{\langle a, b \rangle, \langle b, c \rangle, \langle a, d \rangle, \langle d, e \rangle, \langle f, e \rangle\} $。判断 $ D $ 的性质：

  • $ A. $ 强连通图
  • $ B. $ 单向连通图
  • $ C. $ 弱连通图

  • $ D. $ 不连通图

  • A. 强连通图
    强连通图要求图中任意两点都可以互相到达。从图中可以看出，$ a $ 可以到达 $ b, c, d, e $，但 $ f $ 无法到达任何其它节点，也不能从其它节点到达 $ f $，所以它不是强连通图。

  • B. 单向连通图
    单向连通图是指图中至少存在一条路径使得每一对节点都可以从其中一方到达另一方。这个图是单向连通的，因为从任何节点出发，存在至少一条路径可以到达其它节点（例如 $ a $ 到达 $ b, c, d, e $，且 $ f $ 可以通过 $ e $ 到达 $ d $)。

  • C. 弱连通图
    弱连通图意味着如果将图中的所有边都看作无向边，那么图是连通的。同时，弱连通图还需满足有向图无法两两到达。

  • D. 不连通图
    该图实际上是连通的，因此不是不连通图。

答案: C

问题 4:

集合 $ A = \{a, b, c\} $ 上的下列关系矩阵中符合偏序关系条件的是（ ）

偏序关系的条件：

  1. 自反性：矩阵对角线上的元素必须为 1。
  2. 反对称性：如果 $ (x, y) \in R $ 且 $ (y, x) \in R $，则 $ x = y $。
  3. 传递性：如果 $ (x, y) \in R $ 且 $ (y, z) \in R $，则 $ (x, z) \in R $。

  • D.
    $
    \begin{bmatrix}
    1 & 1 & 1 \\
    0 & 1 & 0 \\
    0 & 1 & 1
    \end{bmatrix}
    $

    • 自反性：对角线为 1，符合自反性。
    • 反对称性：没有违反反对称性。
    • 传递性：符合传递性。

    符合偏序关系。

答案: D

问题 5:

设 $ A = \{1, 2, 3\} $，二元关系 $ S = \{ \langle 1, 1 \rangle, \langle 1, 2 \rangle, \langle 3, 2 \rangle, \langle 3, 3 \rangle \} $，则 $ S $ 是（ ）

选项：

  • A. 自反关系：每个元素与自己有关系，$ \langle 2, 2 \rangle $ 不在 $ S $ 中，因此不是自反关系。
  • B. 传递关系：检查传递性，符合条件。
  • C. 对称关系：如果 $ \langle a, b \rangle \in S $，则 $ \langle b, a \rangle \in S $。此关系中 $ \langle 1, 2 \rangle $ 在 $ S $ 中，但没有 $ \langle 2, 1 \rangle $，因此它不是对称关系。
  • D. 反自反关系：要求每个元素 $ \langle x, x \rangle \notin S $，但 $ \langle 1, 1 \rangle $ 和 $ \langle 3, 3 \rangle $ 存在，所以它不是反自反关系。

答案: B

问题 6:

设 $ A = \{a, b, c, d\} $，$ A $ 上的等价关系 $ R = \{ \langle a, b \rangle, \langle b, a \rangle, \langle c, d \rangle, \langle d, c \rangle \} \cup I_A $，则对应于 $ R $ 的 $ A $ 的划分是（ ）

选项：

  • A. $ \{\{a\}, \{b, c\}, \{d\}\} $：不符合等价关系的划分。
  • B. $ \{\{a, b\}, \{c\}, \{d\}\} $：不符合等价关系的划分。
  • C. $ \{\{a\}, \{b\}, \{c\}, \{d\}\} $：不符合等价关系的划分。
  • D. $ \{\{a, b\}, \{c, d\}\} $：符合等价关系的划分。

答案: D

问题 7:

以下非负整数列可简单图化为一个欧拉图的是（ ）

选项：

  • A. {2, 2, 2, 2, 0}
  • B. {4, 2, 6, 2, 2}
  • C. {2, 2, 3, 4, 1}
  • D. {4, 2, 2, 4, 2}

答案: D

解析：
一个图要是 欧拉图，需要满足以下条件：

  • 所有的顶点的度数都是偶数。

检查各选项的度数列：

  • A. {2, 2, 2, 2, 0}：0不满足条件，因此不是欧拉图。
  • B. {4, 2, 6, 2, 2}：不可能有度数为6的点。
  • C. {2, 2, 3, 4, 1}：度数列中存在奇数（3, 1），因此不是欧拉图。
  • D. {4, 2, 2, 4, 2}：度数全为偶数，符合欧拉图的条件。

答案: D

问题 8:

设论域 $ D = \{a, b\} $，与公式 $ \exists x A(x) $ 等价的命题公式是（ ）

选项：

  • A. $ A(a) \land A(b) $
  • B. $ A(a) \to A(b) $
  • C. $ A(a) \lor A(b) $
  • D. $ A(b) \to A(a) $

答案: C

解析：

  • $ \exists x A(x) $ 的含义是 “存在某个 $ x $，使得 $ A(x) $ 为真”。
  • 在论域 $ D = \{a, b\} $ 上，$ \exists x A(x) $ 的等价命题是 “要么 $ A(a) $ 为真，要么 $ A(b) $ 为真”，即 $ A(a) \lor A(b) $。
  • 所以，正确答案是 $ C $。

答案: C

问题 9:

一棵树有3个4度顶点，4个2度顶点，其余都是树叶，求这棵树有多少个树叶顶点（ ）

选项：

  • A. 12
  • B. 8
  • C. 10
  • D. 13

答案: C

解析：
根据树的性质，树的边数 $ E $ 和顶点数 $ V $ 之间满足 $ E = V - 1 $。

  • 树的度数之和等于两倍的边数，即 $ \sum_{v \in V} \text{deg}(v) = 2E $。
  • 设树的顶点数为 $ V $，树的边数为 $ E = V - 1 $，并且已知：
    • 3个4度顶点，总度数为 $ 3 \times 4 = 12 $。
    • 4个2度顶点，总度数为 $ 4 \times 2 = 8 $。
    • 其余为树叶，度数为1，设树叶个数为 $ L $。

因此，度数之和为 $ 12 + 8 + L = 2E = 2(V - 1) $。

  • 树的顶点数 $ V = L + 7 $（3个4度顶点和4个2度顶点总共7个顶点）。

所以：
$
12 + 8 + L = 2(L + 7 - 1)
$
$
20 + L = 2L + 12
$
$
8 = L
$

因此，树叶顶点的数量是 8，所以正确答案是 C。

答案: C

问题 10:

有A、B、C三个人猜测甲、乙、丙三个球队中的冠军。各人的猜测如下：

  • A: 冠军不是甲，也不是乙。
  • B: 冠军不是甲，而是丙。
  • C: 冠军不是丙，而是甲。

已知其中有一个人说的完全正确，一个人说的都不对，而另外一人恰有一半说对了。根据这些信息推算，冠军应该是（ ）

选项：

  • A. 甲
  • B. 乙
  • C. 丙
  • D. 不确定

答案: A

解析：
我们需要分析三个人的猜测，并确定哪个人说的完全正确，哪个人说的完全不对，哪个人说的一半对。

  • A的猜测： 冠军不是甲，也不是乙。这意味着冠军是丙。
  • B的猜测： 冠军不是甲，而是丙。冠军是丙。
  • C的猜测： 冠军不是丙，而是甲。冠军是甲。

根据题意，其中有一个人说的完全正确，一个人说的完全不对，另一个人说的一半对。我们可以逐一验证每种可能性。

  1. 假设冠军是甲：

    • A 说“冠军不是甲，也不是乙”，这与实际情况不符，因此A完全错。
    • B 说“冠军不是甲，而是丙”，这也与实际情况不符，因此B完全错。
    • C 说“冠军不是丙，而是甲”，这与实际情况完全一致，C完全对。

    结论：如果冠军是甲，那么A和B完全错，C完全对，符合题意。所以，冠军是 甲。

答案: A

问题 11:

如第11题图所示各图，其中存在哈密顿回路的图是（ ）

image-20241118190025421

答案: C

问题 12:

设 $ C(x) $: x 是国家级运动员，$ G(x) $: x 是健壮的，则命题“没有一个国家级运动员不是健壮的”可符号化为（ ）

选项：

  • A. $ \neg \forall x (C(x) \land \neg G(x)) $
  • B. $ \neg \forall x (C(x) \to \neg G(x)) $
  • C. $ \neg \exists x (C(x) \to \neg G(x)) $
  • D. $ \neg \exists x (C(x) \land \neg G(x)) $

答案: D

解析：
命题“没有一个国家级运动员不是健壮的”可以理解为“所有国家级运动员都是健壮的”。符号化表达是：不存在一个国家级运动员，他不是健壮的。即表示“不存在一个 $ x $ 满足 $ C(x) $ 且 $ \neg G(x) $”（即 $ x $ 是国家级运动员但不健壮）。

选项 D 对应的符号化为 $ \neg \exists x (C(x) \land \neg G(x)) $，恰好符合此命题。

答案: D

计算题

问题1：

用等值演算法求取下列公式 $ (\neg P \rightarrow Q) \rightarrow (P \vee \neg Q) $ 的合取范式

步骤解析：

给定公式是 $ (\neg P \rightarrow Q) \rightarrow (P \vee \neg Q) $。我们的目标是通过逻辑等价变换将其转化为合取范式（CNF）。合取范式是由一系列子句（每个子句为文字的合取）组成的合取。

步骤 1: 转化 $ \neg P \rightarrow Q $

首先，使用条件蕴含的逻辑等价式：
$
\neg P \rightarrow Q \equiv P \vee Q
$
所以，公式变为：
$
(P \vee Q) \rightarrow (P \vee \neg Q)
$

步骤 2: 转化 $ (P \vee Q) \rightarrow (P \vee \neg Q) $

同样使用条件蕴含的逻辑等价式 $ A \rightarrow B \equiv \neg A \vee B $：
$
(P \vee Q) \rightarrow (P \vee \neg Q) \equiv \neg (P \vee Q) \vee (P \vee \neg Q)
$
再应用德摩根律：$ \neg (P \vee Q) \equiv \neg P \land \neg Q $，公式变为：
$
(\neg P \land \neg Q) \vee (P \vee \neg Q)
$

步骤 3: 分配律

接下来，应用分配律：
$
(\neg P \land \neg Q) \vee (P \vee \neg Q) \equiv (\neg P \vee (P \vee \neg Q)) \land (\neg Q \vee (P \vee \neg Q))
$

继续简化：

  • $ \neg P \vee (P \vee \neg Q) \equiv (\neg P \vee P \vee \neg Q) \equiv (\text{true} \vee \neg Q) \equiv \text{true} $
  • $ \neg Q \vee (P \vee \neg Q) \equiv (\neg Q \vee P \vee \neg Q) \equiv P \vee \neg Q $

所以，最终的合取范式（CNF）是：
$
P \vee \neg Q
$

答案：

合取范式为 $ P \vee \neg Q $。

问题2：

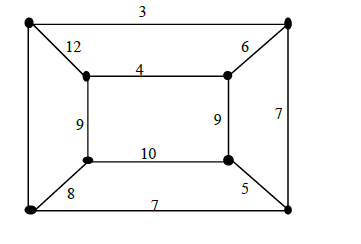
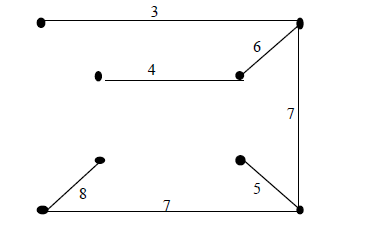
图G 如下图所示，求图G 的最小生成树.（5 分）

image-20241118190540222

image-20241118190619525

问题3：

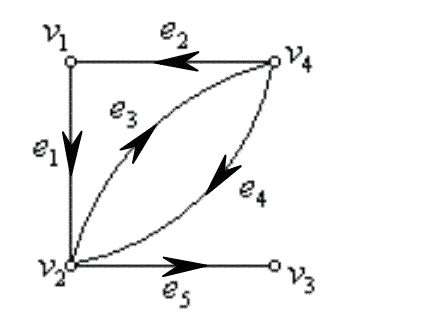
有向图D如图所示，求D的关联矩阵M(D)

image-20241118190735800

image-20241118190919647

最终答案为：image-20241118191046168

问题 4:

化简表达式 $ (((A \cup (B - C)) \cap A) \cup (B - (B - A))) \cap (C - A) $

步骤 1: 化简 $ B - (B - A) $

根据集合差运算的定义，$ B - A $ 表示在 $ B $ 中去除 $ A $ 的元素，所以下式为：
$
B - (B - A) = A
$
因为 $ B - A $ 是 $ B $ 中不属于 $ A $ 的元素，$ B - (B - A) $ 就是 $ B $ 中属于 $ A $ 的元素，也即 $ A $ 本身。

步骤 2: 化简 $ (A \cup (B - C)) \cap A $

先来看 $ A \cup (B - C) $，这是 $ A $ 和 $ B $ 中去除 $ C $ 的部分的并集。然后，我们求交集：
$
(A \cup (B - C)) \cap A
$
由于 $ A $ 和 $ A \cup (B - C) $ 中的元素都至少包含 $ A $ 中的元素，交集必然是 $ A $ 本身。因此：
$
(A \cup (B - C)) \cap A = A
$

步骤 3: 化简 $ (A \cup (B - C)) \cap A \cup (B - (B - A)) $

从前面步骤中我们已经知道：
$
(A \cup (B - C)) \cap A = A \quad \text{且} \quad B - (B - A) = A
$
因此：
$
A \cup A = A
$

步骤 4: 化简 $ ((A \cup (B - C)) \cap A) \cup (B - (B - A)) $ 与 $ (C - A) $ 的交集

最终的表达式是：
$
(A \cup (B - C)) \cap A \cup (B - (B - A)) \cap (C - A)
$
我们已经得到了：
$
A \cup A = A
$
接下来，求与 $ C - A $ 的交集：
$
A \cap (C - A)
$
由于 $ A $ 和 $ C - A $ 之间没有交集（$ C - A $ 表示 $ C $ 中不包含 $ A $ 的元素，而 $ A $ 本身包含在 $ A $ 中），所以交集为：
$
A \cap (C - A) = \emptyset
$

最终答案：

$
\emptyset
$

证明题

问题1：

构造下面推理的证明

前提：

  1. $ p \lor q $
  2. $ p \rightarrow \neg r $
  3. $ s \rightarrow t $
  4. $ \neg s \rightarrow r $
  5. $ \neg t $

结论：
$ q $

证明步骤：

1. 证明的结构：

从给定的前提出发，我们使用合适的逻辑推理规则，逐步得出结论 $ q $。

  1. 假设 $ \neg t $
    这是直接从前提 5 中得出的。

  2. $ s \rightarrow t $
    这是直接从前提 3 得到的。

  3. 假设 $ \neg s $
    这一步使用了拒取式（假设 $ \neg s $ 成立）。

  4. $ \neg s \rightarrow r $
    这是直接从前提 4 得到的。

  5. 得出 $ r $
    由假言推理（前提 4 和 3），从 $ \neg s $ 可得 $ r $。

  6. $ p \rightarrow \neg r $
    这是直接从前提 2 得到的。

  7. 假设 $ p $
    这是拒取式的一部分，假设 $ p $ 成立。

  8. 得出 $ \neg p $
    从 $ p \rightarrow \neg r $ 得到 $ \neg p $。

  9. $ p \lor q $
    这是直接从前提 1 得到的。

  10. 得出 $ q $
    使用析取三段论，由 $ p \lor q $ 和 $ \neg p $，我们得出 $ q $。

解释：

  1. 拒取式（Reductio ad Absurdum）：假设某个命题为假，推导出矛盾，再得出原命题为真。
  2. 假言推理：从 $ A \rightarrow B $ 和 $ A $ 得出 $ B $。
  3. 析取三段论：如果 $ p \lor q $ 为真，且 $ \neg p $ 为真，那么必然 $ q $ 为真。

因此，经过推理的所有步骤后，得出结论 $ q $。

问题2：

设 $ A = \{1, 2, 3, 4\} $，在 $ A \times A $ 上定义二元关系 $ R $，
对于任意 $ \langle u, v \rangle, \langle x, y \rangle \in A \times A $，
$
\langle u, v \rangle R \langle x, y \rangle \iff u + y = x + v
$
证明关系 $ R $ 是 $ A \times A $ 上的等价关系。

答案与解释：

我们需要证明关系 $ R $ 满足以下三个性质：自反性、对称性和传递性。

1) 证明自反性：

自反性要求对于任意 $ \langle u, v \rangle \in A \times A $，都有 $ \langle u, v \rangle R \langle u, v \rangle $。

  • 对于任意 $ \langle u, v \rangle \in A \times A $，我们需要检查是否满足 $ u + v = u + v $。
  • 显然，对于任何 $ u, v \in A $，总有 $ u + v = u + v $ 成立。
  • 因此，$ \langle u, v \rangle R \langle u, v \rangle $ 对所有 $ \langle u, v \rangle \in A \times A $ 成立，关系 $ R $ 满足自反性。

2) 证明对称性：

对称性要求对于任意 $ \langle u, v \rangle, \langle x, y \rangle \in A \times A $，如果 $ \langle u, v \rangle R \langle x, y \rangle $，则必须有 $ \langle x, y \rangle R \langle u, v \rangle $。

  • 假设 $ \langle u, v \rangle R \langle x, y \rangle $，即 $ u + y = x + v $。
  • 我们需要检查是否有 $ x + v = u + y $，显然，由于加法的交换律，$ u + y = x + v $ 蕴含 $ x + v = u + y $。
  • 因此，$ \langle x, y \rangle R \langle u, v \rangle $ 成立，关系 $ R $ 满足对称性。

3) 证明传递性：

传递性要求对于任意 $ \langle u, v \rangle, \langle x, y \rangle, \langle m, n \rangle \in A \times A $，如果 $ \langle u, v \rangle R \langle m, n \rangle $ 且 $ \langle m, n \rangle R \langle x, y \rangle $，则必须有 $ \langle u, v \rangle R \langle x, y \rangle $。

  • 假设 $ \langle u, v \rangle R \langle m, n \rangle $ 和 $ \langle m, n \rangle R \langle x, y \rangle $ 成立，即：

    • $ u + n = m + v $
    • $ m + y = x + n $

    我们需要证明 $ u + y = x + v $。

  • 从第一个方程 $ u + n = m + v $ 解得 $ m = u + n - v $。

  • 将这个代入第二个方程 $ m + y = x + n $，得到：
    $
    (u + n - v) + y = x + n
    $
    简化得到：
    $
    u + y - v = x
    $
    即：
    $
    u + y = x + v
    $

  • 因此，$ \langle u, v \rangle R \langle x, y \rangle $ 成立，关系 $ R $ 满足传递性。

问题3：

已知 $ A $、$ B $、$ C $ 是三个集合，证明：
$
A - (B \cup C) = (A - B) \cap (A - C)
$

1) 证明 $ A - (B \cup C) \subseteq (A - B) \cap (A - C) $：

  • 假设 $ x \in A - (B \cup C) $，根据差集的定义，$ x \in A $ 且 $ x \notin B \cup C $。
  • 由于 $ x \notin B \cup C $，这意味着 $ x \notin B $ 且 $ x \notin C $（因为 $ x \notin B \cup C $ 说明 $ x $ 不属于集合 $ B $ 和 $ C $ 中的任何一个）。
  • 因此，$ x \in A - B $ 且 $ x \in A - C $，即 $ x \in (A - B) \cap (A - C) $。

由此我们证明了：
$
A - (B \cup C) \subseteq (A - B) \cap (A - C)
$

2) 证明 $ (A - B) \cap (A - C) \subseteq A - (B \cup C) $：

  • 假设 $ x \in (A - B) \cap (A - C) $，根据交集的定义，$ x \in A - B $ 且 $ x \in A - C $。
  • 由于 $ x \in A - B $，这意味着 $ x \in A $ 且 $ x \notin B $。
  • 同样，$ x \in A - C $ 表示 $ x \in A $ 且 $ x \notin C $。
  • 因此，$ x \in A $ 且 $ x \notin B $ 且 $ x \notin C $，从而 $ x \notin B \cup C $（因为 $ x $ 不在 $ B $ 和 $ C $ 中的任何一个集合里）。
  • 因此，$ x \in A - (B \cup C) $。

由此我们证明了：
$
(A - B) \cap (A - C) \subseteq A - (B \cup C)
$

3) 结论：

由于我们已经证明了两个包含关系：
$
A - (B \cup C) \subseteq (A - B) \cap (A - C) \quad \text{和} \quad (A - B) \cap (A - C) \subseteq A - (B \cup C)
$
因此，$ A - (B \cup C) = (A - B) \cap (A - C) $ 成立。

问题4：

给定无向图 $ G = (V, E) $，其中 $ |V| = n $ 和 $ |E| = m $，证明以下两个命题是等价命题：

  1. $ G $ 中每对顶点之间具有唯一的通路。
  2. $ G $ 连通且 $ n = m + 1 $。

证明 1) $ \Rightarrow $ 2)

假设 $ G $ 满足条件 1，即每对顶点之间都有唯一的通路。

  1. 证明 $ G $ 连通：
    如果 $ G $ 不是连通的，那么图中至少有两个连通子图。在这两个不同连通子图中的顶点之间没有通路，这与假设“每对顶点之间有唯一的通路”矛盾。因此，$ G $ 必须是连通的。

  2. 证明 $ n = m + 1 $：
    我们将通过数学归纳法证明 $ n = m + 1 $。

    • 基础情况（$ n = 1 $）： 显然，图中只有一个顶点，没有边，所以 $ m = 0 $，满足 $ n = m + 1 $。

    • 假设（$ n = k $ 时结论成立）： 假设当图中有 $ k $ 个顶点时，命题成立，即 $ n = k $ 时 $ m = k - 1 $。

    • 归纳步骤（证明 $ n = k + 1 $ 时 $ m = k $）：
      当图中有 $ k + 1 $ 个顶点时，我们增加一个顶点 $ n_{k+1} $ 并连接原有的 $ k $ 个顶点中的两个顶点 $ n_t $ 和 $ n_p $ 通过一条边。由于根据命题 1 每对顶点之间都有唯一的通路，因此 $ n_{k+1} $ 和其他 $ k $ 个顶点之间不能有两条以上的通路。如果 $ n_{k+1} $ 与 $ k $ 个顶点之间存在两条边，或者与图中原有的顶点不连通，就会与命题 1 矛盾。因此，$ n_{k+1} $ 与原有的 $ k $ 个顶点仅通过一条边相连。根据归纳假设，当 $ n = k $ 时，$ m = k - 1 $，因此当 $ n = k + 1 $ 时，$ m = k $。

    综上所述，当 $ n = k + 1 $ 时，$ m = k $，命题 2 成立。

证明 2) $ \Rightarrow $ 1)

假设 $ G $ 满足条件 2，即 $ G $ 连通且 $ n = m + 1 $。

  1. 证明每对顶点之间有唯一的通路：
    我们将通过数学归纳法证明当 $ G $ 连通且 $ n = m + 1 $ 时，每对顶点之间有唯一的通路。

    • 基础情况（$ n = 1 $ 或 $ n = 2 $）： 显然，当 $ n = 1 $ 时，图中只有一个顶点，没有边，存在唯一的通路。对于 $ n = 2 $ 的情况，图中只有两个顶点和一条边，显然也存在唯一的通路。

    • 假设（当 $ n = k $ 时结论成立）： 假设对于 $ n = k $ 时，图中每对顶点之间有唯一的通路。

    • 归纳步骤（证明 $ n = k + 1 $ 时每对顶点之间有唯一的通路）：
      当图中有 $ k + 1 $ 个顶点时，假设我们增加一个顶点 $ n_{k+1} $，并连接它与原来图中的一个顶点 $ n_t $。由于 $ n = m + 1 $，新增加的边连接原有的 $ k $ 个顶点与 $ n_{k+1} $ 之间仅增加了一条边。我们需要证明，增加新顶点后，图中每对顶点之间依然有唯一的通路。

      • 若 $ n_{k+1} $ 与原图中的其他顶点之间存在多条通路，由于图中每对顶点之间有唯一的通路，这会产生矛盾。假设 $ n_p $ 与 $ n_{k+1} $ 之间存在多条通路，那么 $ n_p $ 必须通过 $ n_t $ 以外的其他路径到达 $ n_{k+1} $，这与唯一通路的假设矛盾。因此，$ n_{k+1} $ 与原图中的顶点之间只能通过一条边连接。

    综上，增加一个顶点后，图中每对顶点之间依然有唯一的通路。

通过以上归纳法，我们证明了当 $ n = m + 1 $ 时，图中每对顶点之间有唯一的通路。