华南理工大学离散数学试卷
华南理工大学期末考试《Discrete Mathematics》
选择题
问题1:
Which is a proposition?
Options:
A) Is the water boiling?
这是一道问题,不是一个陈述。它没有固定的真值(真或假),所以它不是命题。
B) x > 1.5
这是一个包含变量 $x$ 的不等式。由于 $x$ 可以取不同的值,因此该命题的真值依赖于 $x$ 的值,因此它不是命题。
C) There will be no water on the earth after 5000 years.
这是一个可以判断真假的陈述,所以它是一个命题。
D) Help me.
这是一句命令,不是陈述。它没有真值,因此不是命题。
Answer:
C) There will be no water on the earth after 5000 years.
问题2:
The implication $ q \to \neg p $ is true for all possible assignments of truth values to $ p $ and $ q $ except for which assignment?
命题 $ q \to \neg p $ 的真假取决于 $q$ 和 $p$ 的值。根据逻辑,$ q \to \neg p $ 只有在 $q$ 为真且 $ \neg p $ 为假时才为假。换句话说,当 $q$ 为真且 $p$ 为真时,$ q \to \neg p $ 为假。
以下是 $ q \to \neg p $ 的真值表:
| $ p $ | $ q $ | $ \neg p $ | $ q \to \neg p $ |
|---|---|---|---|
| T | T | F | F |
| T | F | F | T |
| F | T | T | T |
| F | F | T | T |
由真值表可知,只有当 $p$ 为真,且 $q$ 为真时,$ q \to \neg p $ 为假。
Answer:
D) p true, q true
问题3:
Which of these statements is a correct translation of the statement: “No Computer Science Major is taking any courses” where $ C(x) $ is the statement “x is a Computer Science Major,” and $ T(x, y) $ is the statement “x is taking y”. Assume that the universe for $ x $ is the set of all students, and the universe for $ y $ is the set of all courses.
这句话的意思是“没有计算机科学专业的学生在修任何课程”,也就是说,对于每个计算机科学专业的学生 $x$,都没有课程 $y$ 是他/她在修的。
正确的翻译应该是:
$
\forall x (C(x) \to \forall y (\neg T(x, y)))
$
意思是对于每个学生 $ x $,如果 $x$ 是计算机科学专业的学生,那么对所有课程 $y$,$ x $ 都没有修 $y$。
Answer:
D) $\neg \exists x\,\exists y\, (C(x)\wedge T(x,y))$
问题4:
Function $ f $ is defined as $ f: \mathbb{Z} \to \mathbb{Z}, f(x) = |x| - 2x $, so $ f $ is ( )
解释:
画图出来会发现该图是一个满射。
问题5:
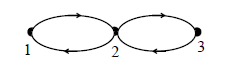
Suppose a binary relation $ R $ (Figure 1) on the set $ A = \{1, 2, 3\} $, $ R $ is ( )
解释:
为了判断关系 $ R $ 的性质,需要了解以下定义:
- 自反性(Reflexive):关系是自反的,当且仅当每个元素都与自己相关联,即对于集合中的每个 $ a \in A $,都满足 $ (a, a) \in R $。
- 非自反性(Irreflexive):关系是非自反的,当且仅当没有任何元素与自己相关联,即对于集合中的每个 $ a \in A $,都满足 $ (a, a) \notin R $。
- 对称性(Symmetric):关系是对称的,当且仅当对于每一对 $ (a, b) \in R $,也满足 $ (b, a) \in R $。
- 反对称性(Antisymmetric):关系是反对称的,当且仅当对于每一对 $ (a, b) \in R $ 且 $ (b, a) \in R $,必须满足 $ a = b $。
- 传递性(Transitive):关系是传递的,当且仅当对于每一对 $ (a, b) \in R $ 和 $ (b, c) \in R $,必须有 $ (a, c) \in R $。
根据图像可以得到是非自反的,堆成的,非传递性的。
问题6:
Which of these arguments is true?
解释:
A) $ (P(S), \subseteq) $ 是一个偏序集(poset)并且是全序的(total ordered)
$ P(S) $ 是 $ S $ 的幂集,而子集关系 $ \subseteq $ 是一个偏序集。但是它并不是总是全序的。一个偏序集是全序的,当且仅当每一对元素都是可比较的,而在幂集的情况下,只有当 $ S $ 是单元素集时,才会是全序的。因此,这个说法是错误的。B) $ (\mathbb{Z}^+, |) $ 是全序的
整数集 $ \mathbb{Z}^+ $ 上的“整除关系” $ | $ 不是全序的。举例来说,2 和 3 之间没有比较关系,因为 2 不能整除 3,反之亦然。所以,这个说法是错误的。C) 整除关系 $ | $ 是正整数集合上的偏序关系,$ (\mathbb{Z}^+, |) $ 是偏序集(poset)
这个说法是正确的。整除关系满足反身性、反对称性和传递性,因此是一个偏序关系。D) $ (\mathbb{N}, \geq) $ 是良序的(well-ordered)
良序集要求每个非空子集都有最小元素,而 $ (\mathbb{N}, \geq) $(自然数集上的大于等于关系)并不是良序的,因为自然数集没有最大元素。因此,这个说法是错误的。
答案:
C) 整除关系“ | ”是正整数集合上的偏序关系,$ (\mathbb{Z}^+, |) $ 是偏序集(poset)
问题7:
$ (A \cup B) - C = $ ( )
解释:
我们来一步步推导这个集合的操作:
- $ A \cup B $ 表示集合 $ A $ 和 $ B $ 的并集,即包含 $ A $ 和 $ B $ 中的所有元素。
- $ (A \cup B) - C $ 表示在集合 $ A \cup B $ 中去除掉集合 $ C $ 中的元素,也就是说要找出在 $ A \cup B $ 中但不在 $ C $ 中的元素。
我们可以将其拆解成两个部分:
- $ (A - C) $:表示从集合 $ A $ 中去除集合 $ C $ 中的元素。
- $ (B - C) $:表示从集合 $ B $ 中去除集合 $ C $ 中的元素。
最终结果是 $ (A - C) \cup (B - C) $,即从 $ A $ 和 $ B $ 中去除掉 $ C $ 的元素后,取并集。
答案:
B) $ (A - C) \cup (B - C) $
问题8:
Which statement is correct?
解释:
我们逐一分析这些选项:
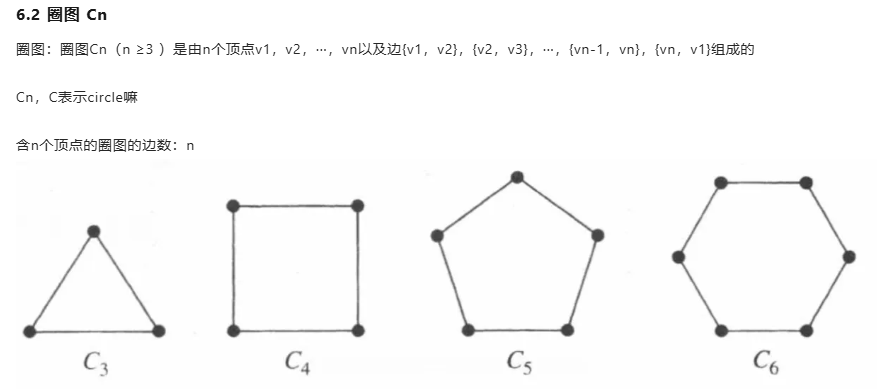
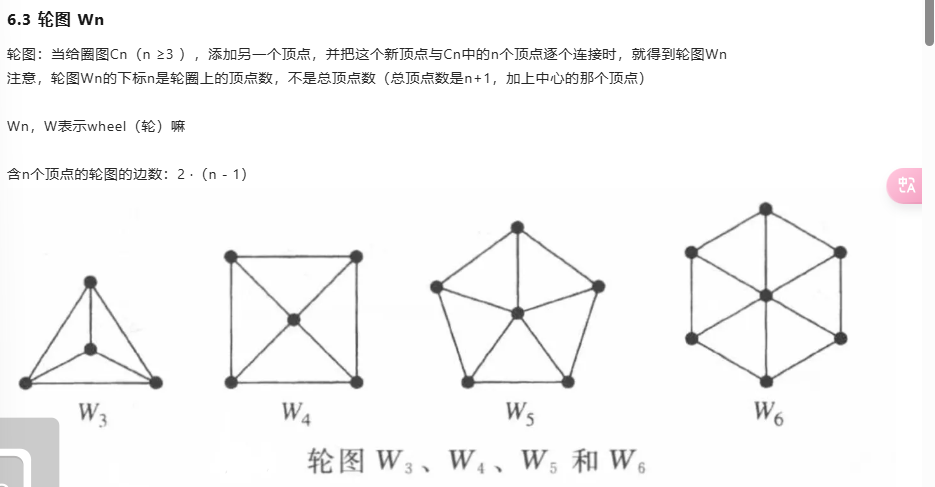
A) There are $ 2n $ 1s and $ n(n-2) $ 0s in the adjacency matrix for $ C_n $.
$ C_n $ 是一个循环图,每个顶点都与前后相邻的两个顶点相连。所以在 $ C_n $ 的邻接矩阵中,每个顶点有两个 1(表示与相邻两个顶点相连),其余的都是 0。因此,每个顶点对应的行和列都应该有 2 个 1,且总共有 $ 2n $ 个 1。因此A是正确的。B) $ C_n $ is always bipartite.
一个图是二分图(bipartite)当且仅当图的顶点可以分成两个互不相交的集合,使得每条边都连接这两个集合中的顶点。循环图 $ C_n $ 是二分图的充要条件是 $ n $ 为偶数。如果 $ n $ 为偶数,$ C_n $ 可以被划分成两部分,因此是二分图;如果 $ n $ 为奇数,$ C_n $ 不是二分图。因此,选项 B 是错误的,因为 $ C_n $ 并不是总是二分图。
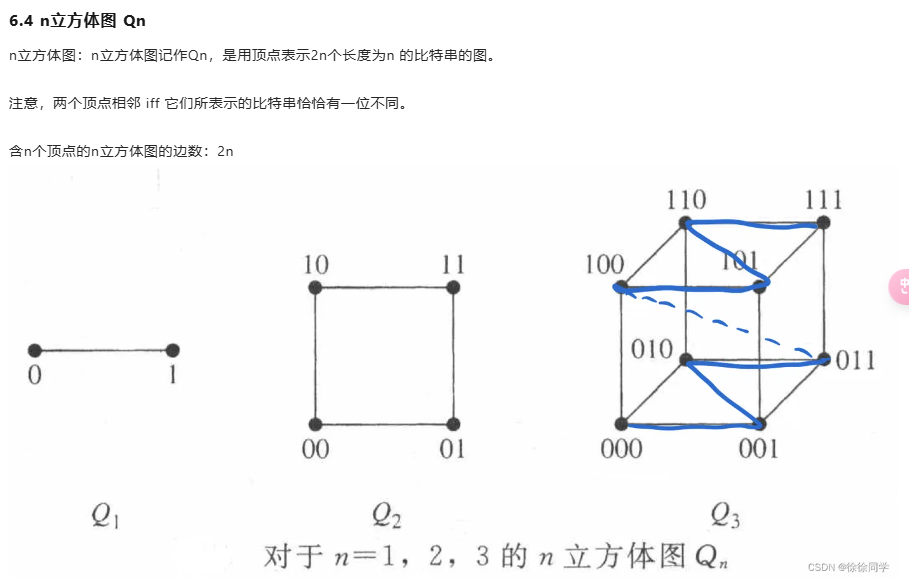
- C) $ Q_n $ has $ n2^n $ edges and $ 2^n $ vertices.
$ Q_n $ 是n维超立方体图,其中有 $ 2^n $ 个顶点。每个顶点与其他顶点的 Hamming 距离为 1 的顶点相连,因此每个顶点有 $ n $ 条边。因此,$ Q_n $ 总共有 $ n \times 2^{n-1} $ 条边,而不是 $ n2^n $ 条边。因此,选项 C 是错误的。
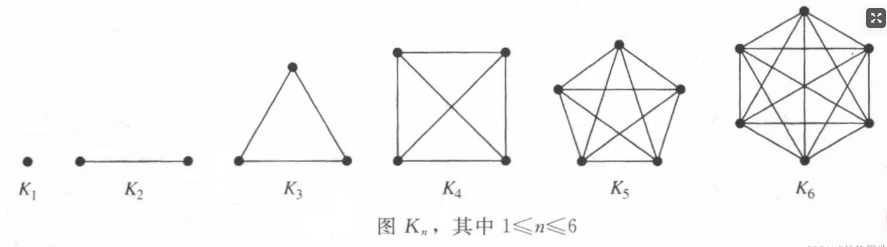
- D) $ K_n $ has $ \frac{n(n+1)}{2} $ edges and $ n $ vertices.
$ K_n $ 是完全图,其中每一对不同的顶点都有一条边。因此,完全图的边数是 $ \frac{n(n-1)}{2} $,而不是 $ \frac{n(n+1)}{2} $。因此,选项 D 是错误的。
答案:
A(这里部分图片参考离散数学_十章-图 ( 2 ):图的术语和几种特殊的图(二)-阿里云开发者社区 (aliyun.com),答谢)
问题9:
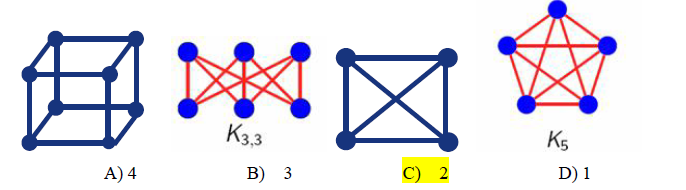
How many planar graphs in the following graphs?
解释:
答案很明显,自然是C。
问题10:
Which statement is wrong?
解释:
让我们逐个分析这些陈述:
- A. If a directed graph is strongly connected, it must be an Euler graph.
强连通图指的是图中的任意两点都有路径可以互相到达。一个欧拉图(Euler graph)是一个每条边恰好经过一次的图。对于有向图,它需要每个顶点的入度等于出度。强连通并不意味着入度和出度相等,因此强连通图不一定是欧拉图。选项 A 是错误的。
反例如下:
B. A graph with a cut edge cannot be an Euler graph.
C. If a graph is an Euler graph, it must be a strongly connected graph.
D. A graph with a cut vertex cannot be a Hamilton graph.
答案:
A) If a directed graph is strongly connected, it must be an Euler graph.
填空题
问题 1:
如果 $ p \rightarrow q $ 为真,判断 $ (p \land q) \rightarrow q $ 的真值。
问题 2:
定义:
- $ C(x): x $ 是一台计算机。
- $ D(x): x $ 是一台外设设备。
- $ P(x, y): x $ 能与 $ y $ 通信。
用逻辑表达式表示“有些计算机无法与某些外设设备通信”。
问题 3:
定义:
- $ l $: Lois 加班。
- $ j $: John 加班。
- $ e $: 他们会在家吃饭。
用逻辑表达式表示:“如果 Lois 或 John 不加班,那么他们会在家吃饭。”
解答:
问题 1:
我们验证 $ (p \land q) \rightarrow q $ 的真值。
分析:
- $ p \rightarrow q $ 表示:如果 $ p $ 为真,则 $ q $ 必为真。
- $ (p \land q) \rightarrow q $ 表示:如果 $ p $ 和 $ q $ 同时为真,那么 $ q $ 必为真。
真值分析:
- $ p \land q $ 成立时,显然 $ q $ 为真。
- 由于 $ p \land q \rightarrow q $ 本质上是自反的恒真公式,因此它的真值总为 真。
答案:$ (p \land q) \rightarrow q $ 的真值为 真。
问题 2:
“有些计算机无法与某些外设设备通信”可以翻译为:
逻辑表达式:
- 存在 $ x $ 和 $ y $,其中 $ x $ 是计算机,$ y $ 是外设,且 $ x $ 无法与 $ y $ 通信。
- $ \exists x \exists y [C(x) \land D(y) \land \neg P(x, y)] $
解释:
- $ \exists x $: 存在一个 $ x $。
- $ \exists y $: 存在一个 $ y $。
- $ C(x) \land D(y) $: $ x $ 是计算机,$ y $ 是外设。
- $ \neg P(x, y) $: $ x $ 无法与 $ y $ 通信。
答案:$ \exists x \exists y [C(x) \land D(y) \land \neg P(x, y)] $
问题 3:
“如果 Lois 或 John 不加班,那么他们会在家吃饭”可以翻译为:
逻辑表达式:
- $ (\neg l \lor \neg j) \rightarrow e $
解释:
- $ \neg l $: Lois 不加班。
- $ \neg j $: John 不加班。
- $ \neg l \lor \neg j $: Lois 或 John 不加班。
- $ \rightarrow e $: 那么他们会在家吃饭。
答案:$ (\neg l \lor \neg j) \rightarrow e $
问题 4
题目:
集合 $ A = \{ l, m, n \} $, $ B = \{ a, b, c \} $, $ C = \{ x, y, z \} $。关系 $ R: A \to B $, $ S: B \to C $,其中:
- $ R = \{ \langle l, b \rangle, \langle m, a \rangle, \langle n, c \rangle \} $
- $ S = \{ \langle a, y \rangle, \langle b, x \rangle, \langle c, y \rangle, \langle c, z \rangle \} $
求复合关系 $ S \circ R $(表示关系 $ R $ 和 $ S $ 的复合)。
解答:
复合关系定义:
- 对于 $ S \circ R $,如果存在一个 $ b \in B $,使得 $ \langle a, b \rangle \in R $ 且 $ \langle b, c \rangle \in S $,那么 $ \langle a, c \rangle \in S \circ R $。
具体计算:
- $ l \to b $(由 $ R $),而 $ b \to x $(由 $ S $),所以 $ l \to x $。
- $ m \to a $(由 $ R $),而 $ a \to y $(由 $ S $),所以 $ m \to y $。
- $ n \to c $(由 $ R $),而 $ c \to y $ 和 $ c \to z $(由 $ S $),所以 $ n \to y $ 和 $ n \to z $。
结果:
- $ S \circ R = \{ \langle l, x \rangle, \langle m, y \rangle, \langle n, y \rangle, \langle n, z \rangle \} $
问题 5
题目:
集合 $ A = \{ \emptyset, \{\emptyset\} \} $,求 $ \rho(A) $(即 $ A $ 的幂集)。
解答:
幂集定义:
- $ \rho(A) $ 是 $ A $ 的所有子集的集合。
- 如果 $ A = \{ x, y \} $,那么 $ \rho(A) $ 包括:
- 空集:$ \emptyset $
- 单元素集:$ \{x\}, \{y\} $
- 全集:$ \{x, y\} $
计算 $ A $ 的子集:
- $ A = \{ \emptyset, \{\emptyset\} \} $
- $ \rho(A) = \{ \emptyset, \{\emptyset\}, \{\{\emptyset\}\}, \{\emptyset, \{\emptyset\}\} \} $
结果:
- $ \rho(A) = \{ \emptyset, \{\emptyset\}, \{\{\emptyset\}\}, \{\emptyset, \{\emptyset\}\} \} $
问题 6
题目:
定义函数 $ f(x) = x + 2 $, $ g(x) = x - 2 $, $ h(x) = 3x $。求复合函数 $ h \circ (g \circ f) $。
解答:
复合函数定义:
- $ g \circ f(x) = g(f(x)) $
- $ h \circ (g \circ f)(x) = h(g(f(x))) $
逐步计算:
- $ f(x) = x + 2 $
- $ g(f(x)) = g(x + 2) = (x + 2) - 2 = x $
- $ h(g(f(x))) = h(x) = 3x $
结果:
- $ h \circ (g \circ f)(x) = 3x $
问题 7
题目:
$ R $ 是整数集合 $ Z \times Z $ 上的“$\geq$”关系,即:
$
(a, b) \in R \iff a \geq b
$
求关系 $ R^{-1} $($ R $ 的逆关系)。
解答:
逆关系定义:
- $ (a, b) \in R^{-1} \iff (b, a) \in R $,即逆关系交换了 $ R $ 中元素的顺序。
计算:
- $ (b, a) \in R $ 意味着 $ b \geq a $。
- 因此,$ (a, b) \in R^{-1} \iff b \geq a $。
结果:
- $ R^{-1} $ 表示“$\leq$”关系。
- 即:
$
R^{-1} = \{ (a, b) \in Z \times Z \mid a \leq b \}
$
答案:$ R^{-1} $ 是“$\leq$”关系。
问题 8
题目:
$ R $ 是“兄弟姐妹”关系(即 $ xRy $ 表示 $ x $ 是 $ y $ 的兄弟姐妹),分析其性质:
- $ R $ 是否反自反(irreflexive)?
- $ R $ 是否自反(reflexive)?
- $ R $ 是否对称(symmetric)?
- $ R $ 是否反对称(antisymmetric)?
- $ R $ 是否传递(transitive)?
解答:
自反性(reflexive/irreflexive):
- 如果 $ R $ 是自反的,则 $ xRx $ 对所有 $ x $ 成立。显然,一个人不能是自己的兄弟姐妹,$ xRx $ 不成立。
- 因此,$ R $ 是反自反(irreflexive)。
对称性(symmetric):
- 如果 $ x $ 是 $ y $ 的兄弟姐妹,那么 $ y $ 也是 $ x $ 的兄弟姐妹。
- $ R $ 满足对称性(symmetric)。
反对称性(antisymmetric):
- 如果 $ R $ 是反对称的,则 $ xRy \land yRx $ 应导致 $ x = y $。显然,兄弟姐妹关系不满足这一条件。
- $ R $ 不满足反对称性(antisymmetric)。
传递性(transitive):
- 如果 $ x $ 是 $ y $ 的兄弟姐妹,且 $ y $ 是 $ z $ 的兄弟姐妹,能保证 $ x $ 是 $ z $ 的兄弟姐妹。
- $ R $ 满足传递性(transitive)。
问题 9
题目:
完全二分图 $ K_{m, n} $ 有多少条割边(cut edges)?
解答:
完全二分图 $ K_{m, n} $ 定义:
- $ K_{m, n} $ 是一个二分图,由两个不相交的顶点集 $ U $ 和 $ V $ 构成,其中:
- $ |U| = m $
- $ |V| = n $
- $ K_{m, n} $ 中每个 $ U $ 中的顶点与 $ V $ 中的所有顶点都有一条边。
- $ K_{m, n} $ 是一个二分图,由两个不相交的顶点集 $ U $ 和 $ V $ 构成,其中:
割边定义:
- 一条边是割边(cut edge),如果删除它会导致图的连通分量数增加。
性质分析:
- 在 $ K_{m, n} $ 中,每条边都唯一连接 $ U $ 和 $ V $。
- 如果删除任意一条边,两个顶点所在的连通性被破坏,图的连通性减少。
- 因此,$ K_{m, n} $ 的所有边都是割边。
边数计算:
- $ K_{m, n} $ 的总边数为:
$
m \times n
$
- $ K_{m, n} $ 的总边数为:
答案:$ K_{m, n} $ 有 $ m \times n $ 条割边。
问题 10
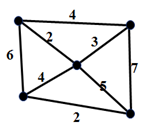
题目:
计算右侧图中最小生成树的边权和。
2+3+4+2=11。
证明题
问题1:
证明以下谓词的等价性:
$
(\forall x)(\forall y)(P(x) \rightarrow Q(y)) \iff (\exists x)P(x) \rightarrow (\forall y)Q(y)
$
我们需要证明以下两个谓词是逻辑等价的:
左边 ($\forall x \forall y (P(x) \rightarrow Q(y))$):
- 这表示对于 所有 $x$ 和 $y$,如果 $P(x)$ 为真,则 $Q(y)$ 必须为真。换句话说,针对每个 $x$,如果 $P(x)$ 为真,那么对于 所有 $y$,$Q(y)$ 必须为真。
右边 ($(\exists x)P(x) \rightarrow (\forall y)Q(y)$):
- 这表示如果 存在 某个 $x$ 使得 $P(x)$ 为真,那么对于 所有 $y$,$Q(y)$ 必须为真。
第一步:证明 $(\forall x \forall y (P(x) \rightarrow Q(y))) \rightarrow ((\exists x)P(x) \rightarrow (\forall y)Q(y))$
- 假设 $(\forall x)(\forall y)(P(x) \rightarrow Q(y))$ 为真。
- 这意味着对于所有的 $x$ 和 $y$,如果 $P(x)$ 为真,则 $Q(y)$ 必须为真。
- 如果 $(\exists x)P(x)$ 为真(即存在某个 $x_0$ 使得 $P(x_0)$ 为真),那么对于 所有 $y$,$Q(y)$ 必须为真。因为对于这个特定的 $x_0$,$(P(x_0) \rightarrow Q(y))$ 对所有 $y$ 都成立,从而 $Q(y)$ 必须对所有 $y$ 都为真。
- 因此,$(\exists x)P(x) \rightarrow (\forall y)Q(y)$ 成立。
第二步:证明 $(\exists x)P(x) \rightarrow (\forall y)Q(y) \rightarrow (\forall x \forall y (P(x) \rightarrow Q(y)))$
- 假设 $(\exists x)P(x) \rightarrow (\forall y)Q(y)$ 为真。
- 我们需要证明 $(\forall x \forall y)(P(x) \rightarrow Q(y))$ 为真。
- 如果 $(\exists x)P(x)$ 为真,那么根据假设 $(\forall y)Q(y)$ 必须为真。即对于所有的 $y$,$Q(y)$ 都为真,这样 $P(x) \rightarrow Q(y)$ 对于所有的 $x$ 和 $y$ 都自然成立,因为 $Q(y)$ 总是为真,保证了前提为真时结论为真。
- 如果 $(\exists x)P(x)$ 不为真,那么 $P(x)$ 对所有的 $x$ 都为假,这样 $P(x) \rightarrow Q(y)$ 对所有 $x$ 和 $y$ 都为真,因为当命题的前提 $P(x)$ 为假时,蕴涵式 $P(x) \rightarrow Q(y)$ 总是成立。
- 因此,$(\forall x \forall y)(P(x) \rightarrow Q(y))$ 也成立。
结论:
因为我们已经证明了双向蕴涵:
- $(\forall x)(\forall y)(P(x) \rightarrow Q(y)) \rightarrow (\exists x)P(x) \rightarrow (\forall y)Q(y)$
- $(\exists x)P(x) \rightarrow (\forall y)Q(y) \rightarrow (\forall x)(\forall y)(P(x) \rightarrow Q(y))$
所以我们可以得出结论:
$
(\forall x)(\forall y)(P(x) \rightarrow Q(y)) \iff (\exists x)P(x) \rightarrow (\forall y)Q(y)
$
因此,两个谓词是等价的。
问题2:
给定前提 $\neg A \lor B$, $\neg C \rightarrow \neg B$, 和 $C \rightarrow D$,如何得出结论 $A \rightarrow D$?
步骤 1: 假设 $A$ 为真
我们假设 $A$ 为真,然后尝试推导出 $D$ 为真。为了完成这一步,我们需要根据前提进行推理。
步骤 2: 使用前提 $\neg A \lor B$
根据第一个前提 $\neg A \lor B$,我们知道:
- 如果 $A$ 为真,则 $\neg A$ 为假。因此,根据 $\neg A \lor B$ 这一析取公式,$B$ 必须为真。
因此,我们得出 $B$ 为真。
步骤 3: 使用前提 $\neg C \rightarrow \neg B$
根据第二个前提 $\neg C \rightarrow \neg B$,即“如果 $\neg C$ 为真,则 $\neg B$ 为真”。我们已经知道 $B$ 为真,因此 $\neg B$ 为假。根据假设和蕴含的逆否命题规则,$\neg C$ 必须为假。也就是说,$C$ 必须为真。
步骤 4: 使用前提 $C \rightarrow D$
根据第三个前提 $C \rightarrow D$,即“如果 $C$ 为真,则 $D$ 为真”。由于我们已知 $C$ 为真,因此可以推导出 $D$ 为真。
步骤 5: 结论 $A \rightarrow D$
我们已经证明了如果 $A$ 为真,则 $D$ 为真。因此,结论 $A \rightarrow D$ 是正确的。
- 我们假设 $A$ 为真,并逐步应用给定的前提来推导出 $D$ 为真。
- 首先,使用 $\neg A \lor B$ 得出 $B$ 为真。
- 接着,通过 $\neg C \rightarrow \neg B$ 得出 $C$ 必须为真。
- 最后,通过 $C \rightarrow D$ 推导出 $D$ 为真。
- 由此可得结论 $A \rightarrow D$。
问题3:
我们给定一个集合 $ A = \{a, b, c, d\} $ 和一个关系 $ R = \{(a, b), (b, a), (b, c), (c, d)\} $,要求使用零一矩阵表示法找出关系 $ R $ 的 传递闭包。
第一步:构造零一矩阵
我们根据关系 $ R $ 构造一个零一矩阵。矩阵的行和列对应集合 $ A = \{a, b, c, d\} $ 中的元素。如果 $ (i, j) $ 是关系 $ R $ 中的元素,则在矩阵中第 $ i $ 行第 $ j $ 列的位置填入 1,否则填入 0。
关系 $ R $ 中包含:
- $ (a, b) $,所以 $ M[1, 2] = 1 $
- $ (b, a) $,所以 $ M[2, 1] = 1 $
- $ (b, c) $,所以 $ M[2, 3] = 1 $
- $ (c, d) $,所以 $ M[3, 4] = 1 $
因此,矩阵 $ M $ 为:
$
M =
\begin{bmatrix}
0 & 1 & 0 & 0 \\
1 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0
\end{bmatrix}
$
第二步:计算传递闭包
传递闭包是关系 $ R $ 的最小闭包,满足如果 $ (a, b) \in R $ 且 $ (b, c) \in R $,则 $ (a, c) $ 也应该在传递闭包中。我们可以使用 Warshall 算法 或者矩阵乘法来计算。
Warshall 算法:
Warshall 算法通过矩阵的幂迭代来计算传递闭包。具体步骤如下:
- 初始化矩阵 $ M $,表示最初的关系。
- 对于每一个节点 $ k $,更新矩阵,使得对于每一对节点 $ i $ 和 $ j $,如果存在路径 $ i \to k \to j $,则设置 $ M[i][j] = 1 $。
我们需要通过中间节点 $ k $ 来迭代更新矩阵。
步骤更新:
对于 $ k = 1 $(节点 $ a $):
- 检查是否通过 $ a $ 形成了新路径,但此时没有新的路径需要添加。
对于 $ k = 2 $(节点 $ b $):
检查是否通过 $ b $ 形成了新路径:
- $ M[1, 3] $ 变为 1,因为存在从 $ a \to b \to c $ 的路径。
- $ M[1, 4] $ 变为 1,因为存在从 $ a \to b \to c \to d $ 的路径。
- $ M[2, 4] $ 变为 1,因为存在从 $ b \to c \to d $ 的路径。
……
对于 $ k = 3 $(节点 $ c $):
- 检查是否通过 $ c $ 形成了新路径,但此时没有新的路径需要添加。
对于 $ k = 4 $(节点 $ d $):
- 检查是否通过 $ d $ 形成了新路径,但此时没有新的路径需要添加。
第三步:得到传递闭包矩阵
经过以上步骤更新后,最终的传递闭包矩阵为:
$
M_{transitive} =
\begin{bmatrix}
1 & 1 & 1 & 1 \\
1 & 0 & 1 & 1 \\
0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0
\end{bmatrix}
$
解释:
- 这个矩阵表示关系 $ R $ 的传递闭包。
- 我们可以看到:
- 从 $ a $ 可以通过直接或间接的路径到达 $ b $、$ c $ 和 $ d $。
- 从 $ b $ 可以通过直接或间接的路径到达 $ a $、$ c $ 和 $ d $。
- 从 $ c $ 可以通过直接或间接的路径到达 $ d $。
因此,传递闭包包含以下关系:
$
\{ (a,a),(a, b), (a, c), (a, d), (b, a), (b, c), (b, d), (c, d) \}
$
问题4:
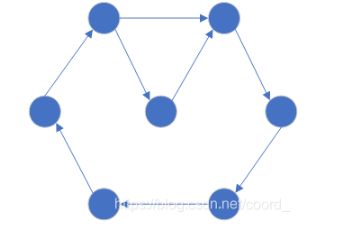
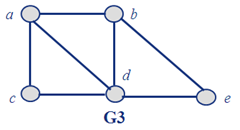
给定一个图,问这个图是否可以用一笔画完?为什么?
答案:
可以画,如果图是连通的且具有0个或2个奇度顶点,则可以用一笔画完。
d和a。
问题5:
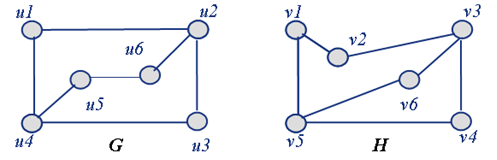
判断图 $ G $ 和图 $ H $ 是否同构。无论判断结果如何,请给出解释和论证。
经过度数验证,成立。
应用题
问题1:
使用推理从前提中得出结论:
- 所有喜欢走路的人都不喜欢开车。
- 每个人都喜欢开车或骑车。
- 有些人不喜欢骑车。
因此,结论是:有些人不喜欢走路。
解答:
我们将逐步分析前提,应用推理规则得出结论。
前提分析:
前提1:所有喜欢走路的人都不喜欢开车
用符号表示为:
$ L(x) \Rightarrow \neg D(x) $
其中,$ L(x) $ 表示“$ x $ 喜欢走路”,而 $ D(x) $ 表示“$ x $ 喜欢开车”。
这个前提意味着,如果某个人喜欢走路,则他们不喜欢开车。前提2:每个人都喜欢开车或骑车
用符号表示为:
$ D(x) \vee R(x) $
其中,$ R(x) $ 表示“$ x $ 喜欢骑车”。
这个前提意味着每个人要么喜欢开车,要么喜欢骑车。前提3:有些人不喜欢骑车
这意味着存在一个人 $ x $ 使得 $ \neg R(x) $,即有些人不喜欢骑车。
推理过程:
根据这些前提,我们可以逐步推导:
从前提3:有些人不喜欢骑车,我们可以得出,至少存在一个人 $ x $ 满足 $ \neg R(x) $。
根据前提2:每个人都喜欢开车或骑车,对于这个人 $ x $,如果他们不喜欢骑车 $ (\neg R(x)) $,根据前提2的排中律,必定喜欢开车 $ (D(x)) $。
现在我们知道这个人 $ x $ 喜欢开车 $ (D(x)) $,根据前提1,如果一个人喜欢走路,则他们不喜欢开车。因此,这个人不可能是喜欢走路的。也就是说,这个人不喜欢走路 $ (\neg L(x)) $。
由于至少存在这样一个人 $ x $,我们可以得出结论:有些人不喜欢走路。
结论:
有些人不喜欢走路。
问题2:
假设 $ R $ 是集合 $ A $ 上的一个自反且传递的关系。 $ T $ 也是集合 $ A $ 上的一个关系,满足:
$
\langle a, b \rangle \in T \Leftrightarrow \langle a, b \rangle \in R \text{ 且 } \langle b, a \rangle \in R
$
证明:$ T $ 是一个等价关系。
解答:
为了证明 $ T $ 是等价关系,我们需要证明 $ T $ 满足等价关系的三个条件:
- 自反性:对于任意 $ a \in A $,有 $ \langle a, a \rangle \in T $。
- 对称性:对于任意 $ a, b \in A $,如果 $ \langle a, b \rangle \in T $,则 $ \langle b, a \rangle \in T $。
- 传递性:对于任意 $ a, b, c \in A $,如果 $ \langle a, b \rangle \in T $ 且 $ \langle b, c \rangle \in T $,则 $ \langle a, c \rangle \in T $。
证明:
自反性:
- 因为 $ R $ 是自反的,即对于所有 $ a \in A $,有 $ \langle a, a \rangle \in R $。
- 根据 $ T $ 的定义,若 $ \langle a, a \rangle \in R $ 且 $ \langle a, a \rangle \in R $,那么 $ \langle a, a \rangle \in T $。
- 因此,$ T $ 是自反的。
对称性:
- 假设 $ \langle a, b \rangle \in T $,则根据 $ T $ 的定义,$ \langle a, b \rangle \in R $ 且 $ \langle b, a \rangle \in R $。
- 由于 $ R $ 是对称的(反映在 $ \langle a, b \rangle \in R $ 和 $ \langle b, a \rangle \in R $ 上),因此 $ \langle b, a \rangle \in T $。
- 因此,$ T $ 是对称的。
传递性:
- 假设 $ \langle a, b \rangle \in T $ 且 $ \langle b, c \rangle \in T $。
- 根据 $ T $ 的定义,$ \langle a, b \rangle \in R $ 且 $ \langle b, a \rangle \in R $,并且 $ \langle b, c \rangle \in R $ 且 $ \langle c, b \rangle \in R $。
- 因为 $ R $ 是传递的,所以从 $ \langle a, b \rangle \in R $ 和 $ \langle b, c \rangle \in R $,可以得出 $ \langle a, c \rangle \in R $。
- 同时,由于 $ \langle a, b \rangle \in R $ 且 $ \langle b, a \rangle \in R $,也有 $ \langle c, b \rangle \in R $ 且 $ \langle b, c \rangle \in R $。
- 所以 $ \langle a, c \rangle \in T $。
- 因此,$ T $ 是传递的。
结论:
由于 $ T $ 满足自反性、对称性和传递性,因此 $ T $ 是一个等价关系。
解释:
- 自反性:每个元素都与自己相关,因为 $ R $ 是自反的,满足 $ \langle a, a \rangle \in T $。
- 对称性:如果 $ a $ 与 $ b $ 相关,那么 $ b $ 也与 $ a $ 相关,因为 $ R $ 本身是对称的。
- 传递性:如果 $ a $ 与 $ b $ 相关,且 $ b $ 与 $ c $ 相关,那么 $ a $ 与 $ c $ 也相关,因为 $ R $ 是传递的。
综上,$ T $ 是等价关系。
问题3:
6个人需要分成3组(每组2人)来完成3个任务。每一组的人应该互相合作完成任务。已知每个人至少能与其他3个人合作。问:是否可能所有的任务都能完成?
解答:
要解决这个问题,我们需要从图论的角度来考虑。
1. 问题转化为图论问题:
我们可以将问题转化为一个图论问题,其中每个人是图中的一个顶点,每个人能合作的人(即能一起完成任务的人)之间有一条边。题目中给出了每个人能与至少3个人合作,也就是说每个人的度数(与该人合作的人数)至少为3。
- 我们有6个人,因此我们有6个顶点。
- 我们需要将这些顶点分成3对,即组成3组,每组2人,表示他们可以一起完成一个任务。
2. 必要条件:
为了完成所有任务,每一对人(组)都必须能互相合作。这意味着,我们必须从这些6个顶点中选出3对,使得每对之间有边连接。这就要求图中的顶点可以分成3个互不重叠的对。
3. 每个人至少能与3个人合作:
每个人至少与3个人合作,这意味着每个顶点的度数至少为3。这样的一组顶点可以被认为是一个“度数至少为3”的图。
4. 是否能分成3组:
我们需要检查是否能把这些6个顶点分成3对,且每一对之间都有边相连。由于每个人至少能与3个人合作,且我们有6个人,总共12个合作关系(即12条边)。这些边足够将6个顶点分成3对,完成任务。
5. 是否可行:
根据题目的要求和图论中的匹配定理,我们可以发现,若每个人的度数至少为3,则有可能将这些人分成3组,使得每组能共同完成任务。
- 具体来说,在一个6个顶点的图中,如果每个顶点的度数至少为3,那么总是能够找到一个匹配,使得每对顶点都有边相连。换句话说,所有任务是可以分配的。
(其实完全图就可以解决)
问题4:
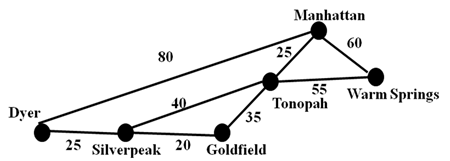
一张图中的边表示小镇之间的未铺设道路,边的权重表示每条道路的长度。需要选择哪些道路进行铺设,才能满足以下条件:
- 在每对小镇之间都有铺设道路的通路。
- 铺设的道路总长度最小。
解答:
该问题可以用 最小生成树(Minimum Spanning Tree, MST)来解决。最小生成树是一棵子图,它连接图中的所有顶点(小镇),且边的权重总和最小。
采用Kruskal算法,即可解决。