华南理工大学10年数据结构B卷
10年数据结构B卷
这是一张不错的,具有含金量的试卷。
选择题
Question: An algorithm must be or do all of the following EXCEPT: ( C )
- Correct
- Unambiguous
- General steps
- Terminate
Answer: C) General steps
Explanation:
- (A) Correct: An algorithm must produce the correct result and meet the expected output.
- (B) Unambiguous: The steps of the algorithm must be clearly defined, with no ambiguity in the execution.
- (C) General steps: While an algorithm typically involves specific steps, these steps do not have to be "general." The steps should be tailored to solve the particular problem, so they are not necessarily general.
- (D) Terminate: An algorithm must terminate in a finite amount of time. If it doesn't, it would run indefinitely, failing to produce a result.
(4) Which statement is not correct among the following four? ( A )
- The number of empty sub-trees in a non-empty binary tree is one less
than the number of nodes in the tree.
- The Mergesort is a stable sorting algorithm.
- A general tree can be transferred to a binary tree with the root
having only left child.
- A sector is the smallest unit of allocation for a record, so all records occupy a multiple of the sector size.
Answer: (A) The number of empty sub-trees in a non-empty binary tree is one less than the number of nodes in the tree.
Explanation:
- (A): This statement is incorrect. In a binary tree, every node has either zero, one, or two children. Each leaf node has two empty sub-trees (left and right), and non-leaf nodes typically have at least one empty subtree (if they have one child). Therefore, the number of empty sub-trees is not necessarily one less than the number of nodes.
- (B): Correct. Mergesort is a stable sorting algorithm, meaning that it preserves the relative order of records with equal keys.
- (C): Correct. A general tree can be converted into a binary tree where each node’s left child represents the first child in the general tree, and the right child represents the next sibling.
- (D): Correct. A sector is the smallest unit of allocation for a record in some file systems, and records are typically stored in multiples of the sector size.
(9) Which queries are supported by both the hashing and tree indexing methods? ( D )
- Range queries.
- Queries in key order.
- Minimum or maximum queries.
- Exact-match queries.
Answer: (D) Exact-match queries.
Explanation:
- (A): Incorrect. Range queries are generally better supported by tree-based indexing (like B-trees) since they allow sequential access. Hashing typically does not support efficient range queries.
- (B): Incorrect. Queries in key order are efficiently supported by tree-based indexing (like B-trees), but not by hashing, as hashing provides no inherent order of keys.
- (C): Incorrect. Minimum or maximum queries are efficiently supported by tree indexing methods (such as binary search trees), but hashing doesn't support this directly.
- (D): Correct. Both hashing and tree indexing methods are efficient for exact-match queries, where a query is looking for a specific key in the data structure.
填空题
(2) A full 8-ary tree with 100 internal nodes has 701 leaves. (4 scores)
Answer: 701 leaves
Explanation:
In a full 8-ary tree, every internal node has exactly 8 children. To
calculate the number of leaves (L) in such a tree, we can use the
relationship between the number of internal nodes (I) and leaves (L) in
a full m-ary tree, which is given by:
$ L = 8I + 1 $
For this problem, $ I = 100 $ (internal nodes), so:
$ L = 8 + 1 = 800 + 1 =801 $
Thus, the tree has 801-100= 701 leaves.
(3) The number of different shapes of binary trees with 6 nodes is 132. (4 scores)
Answer: 132 different shapes
Explanation:
The number of distinct shapes (or structures) of binary trees with $ n $
nodes is given by the nth Catalan number. The Catalan
number for $ n $ nodes is calculated using the formula:
$ C_n = $
For $ n = 6 $:
$ C_6 = = $
Calculating this:
$ C_6 = 132 $
Thus, the number of different shapes of binary trees with 6 nodes is 132.
拓补排序
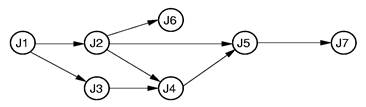
Question: Show an acceptable topological sort for a series of jobs with some prerequisites as shown in the figure. (4 scores)
Jobs: J1, J3, J2, J6, J4, J5, J7
Answer: The topological sort of the jobs could be:
建堆
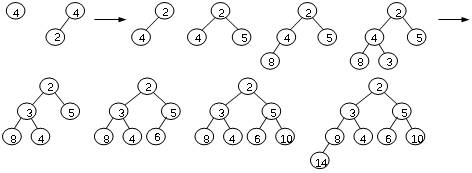
Question:
Show the min-heap that results from running buildheap on
the following values stored in an array: 4, 2, 5, 8, 3, 6, 10, 14. (6
scores)
基数排序
终于考到一道不是快速排序的题目了,太不容易了。
问题: 手动跟踪执行 Radix-sort 算法在数组
a[] = {265, 301, 751, 129, 937, 863, 742, 694, 076, 438}
上的过程,并输出每一轮的结果。
初始数组:
265, 301, 751, 129, 937, 863, 742, 694, 076, 438
Pass 1 (按个位数排序):
- 首先,按个位数排序:
265 → 5
301 → 1
751 → 1
129 → 9
937 → 7
863 → 3
742 → 2
694 → 4
076 → 6
438 → 8
- 排序后按个位数分组:
[301 751] [742] [863] [694] [265] [076] [937] [438] [129]
Pass 2 (按十位数排序):
- 接下来,按十位数排序:
301 → 0
751 → 5
129 → 2
937 → 3
863 → 6
742 → 4
694 → 9
265 → 6
076 → 7
438 → 3
- 排序后按十位数分组:
[301] [] [129] [937 438] [742] [751] [863 265] [076] [] [694]
Pass 3 (按百位数排序):
- 最后,按百位数排序:
301 → 3129 → 1265 → 2937 → 9863 → 8742 → 7694 → 6076 → 0438 → 4751 → 7 - 排序后按百位数分组:
[076] [129] [265] [301] [438] [694] [742 751] [863] [937]
最终排序结果:
最终得到的排序数组是:
076, 129, 265, 301, 438, 694, 742, 751, 863, 937
解释:
- Pass 1 (按个位数排序):每个数字根据个位数进行分类,得到不同的桶。此时,最小的个位数(1)排在前面,而最大个位数(9)排在后面。
- Pass 2 (按十位数排序):对于每个桶中的数字,按十位数进行进一步排序。此时,我们会对每个桶内的数字根据十位数的值进行排列。
- Pass 3 (按百位数排序):对每个桶中的数字按百位数进行分类排序,将百位数字相同的归为一组,比如百位是 0 的归一组,百位是 1 的归一组等等,最终使得所有数字按照从小到大的顺序排列好,得到最终的有序数组。
Radix - sort
算法是一种稳定的排序算法,通过多次按位数分组,使数组元素最终排列成有序状态。
之前百位数排序那里出现了错误的对应情况(比如 301 → 0
这种错误写法),现已改正过来,使其符合正确的基数排序按位分类的逻辑,从而能准确得出最终正确的排序结果。
哈希
问题:
使用闭式哈希(Closed Hashing)方法,并且通过双重哈希(Double
Hashing)来解决冲突,将以下键值插入到一个大小为11的哈希表中(哈希表的槽位编号从0到10)。给定的哈希函数如下:
- $ H_1(k) = 3k $
- $ H_2(k) = 7k + 1 $
给定的键值为:22, 41, 53, 46, 30, 13, 1, 67。请展示在插入所有键值后的哈希表,并说明如何使用哈希函数
$ H_1 $ 和 $ H_2 $ 来进行哈希计算。
答案及解决过程:
- 插入 22:
- 使用哈希函数 $ H_1(22) = 3 = 66 = 0 $
- 22 插入哈希表的槽位 0。
- 哈希表状态:
[22, _, _, _, _, _, _, _, _, _, _]
- 插入 41:
- 使用哈希函数 $ H_1(41) = 3 = 123 = 2 $
- 41 插入哈希表的槽位 2。
- 哈希表状态:
[22, _, 41, _, _, _, _, _, _, _, _]
- 插入 53:
- 使用哈希函数 $ H_1(53) = 3 = 159 = 5 $
- 53 插入哈希表的槽位 5。
- 哈希表状态:
[22, _, 41, _, _, 53, _, _, _, _, _]
- 插入 46:
- 使用哈希函数 $ H_1(46) = 3 = 138 = 6 $
- 46 插入哈希表的槽位 6。
- 哈希表状态:
[22, _, 41, _, _, 53, 46, _, _, _, _]
- 插入 30 (处理冲突):
- 使用哈希函数 $ H_1(30) = 3 = 90 = 2 $
- 由于槽位 2 已经有 41,所以发生冲突,使用第二个哈希函数 $ H_2(30) = 7 + 1 = 210 + 1 = 0 + 1 = 1 $ 来计算步长。
- 计算新的槽位:$ (H_1(30) + H_2(30) ) = (2 + 1 ) = 3 $
- 30 插入哈希表的槽位 3。
- 哈希表状态:
[22, _, 41, 30, _, 53, 46, _, _, _, _]
- 插入 13 (处理冲突):
- 使用哈希函数 $ H_1(13) = 3 = 39 = 6 $
- 由于槽位 6 已经有 46,所以发生冲突,使用第二个哈希函数 $ H_2(13) = 7 + 1 = 91 + 1 = 1 + 1 = 2 $ 来计算步长。
- 计算新的槽位:$ (H_1(13) + H_2(13) ) = (6 + 1 ) = 8 $
- 13 插入哈希表的槽位 8。
- 哈希表状态:
[22, _, 41, 30, _, 53, 46, _, 13, _, _]
- 插入 1 (处理冲突):
- 使用哈希函数 $ H_1(1) = 3 = 3 = 3 $
- 由于槽位 3 已经有 30,所以发生冲突,使用第二个哈希函数 $ H_2(1) = 7 + 1 = 7 + 1 = 7 + 1 = 8 $ 来计算步长。
- 计算新的槽位:$ (H_1(1) + H_2(1) ) = (3 + 1 ) = 11 = 0 $
- 槽位 0 已经有
22,因此再次发生冲突。再一次使用第二个哈希函数来更新步长,计算新的槽位:
$ (H_1(1) + H_2(1) ) = (3 + 2 ) = (3 + 16) = 19 = 8 $ - 插入 1
后,哈希表状态:
[22, _, 41, 30, _, 53, 46, _, 13, _, 1]
- 插入 67 (处理冲突):
- 使用哈希函数 $ H_1(67) = 3 = 201 = 3 $
- 由于槽位 3 已经有 30,因此发生冲突,使用第二个哈希函数 $ H_2(67) = 7 + 1 = 469 + 1 = 9 + 1 = 10 $ 来计算步长。
- 计算新的槽位:$ (H_1(67) + H_2(67) ) = (3 + 1 ) = 13 = 2 $
- 由于槽位 2 已经有 41,发生冲突。再使用第二个哈希函数来更新步长: $ (H_1(67) + H_2(67) ) = (3 + 2 ) = (3 + 20) = 23 = 1 $
- 67 插入哈希表的槽位 1。
- 哈希表状态:
[22, 67, 41, 30, _, 53, 46, _, 13, _, 1]
最终哈希表:
[22, 67, 41, 30, _, 53, 46, _, 13, _, 1]
解释:
- 哈希表的槽位编号从 0 到 10,其中每个键值根据 $ H_1 $ 和 $ H_2 $ 的结果逐步插入。
- 双重哈希通过冲突处理(即使用 $ H_2 $ 来计算步长并调整位置)来确保所有键值成功插入。
图论
刚刚遇到一个误区,这里需要纠正一下, 免得误人子弟。
假设每个顶点索引需要 2 字节,一个指针需要 4 字节,边的权重需要 2 字节。那么,每个邻接表中的链表节点需要 2 + 2 + 4 = 8 字节。
对于有向图:
- 邻接矩阵需要的空间为:
2 * |V|^2 = 50字节。 - 邻接表需要的空间为:
4 * |V| + 8 * |E| = 68字节。
对于无向图:
- 邻接矩阵需要的空间与有向图相同,仍然是
2 * |V|^2 = 50字节。 - 邻接表需要的空间为:
4 * |V| + 8 * |E| = 116字节(因为边的数量从 6 增加到 12)。
外部排序
问题:
简要描述外部排序的两个阶段的主要任务。(4分)
假设工作内存为 256KB,分成 8192 字节的块(另外还有空间用于 I/O 缓冲区、程序变量等)。请计算使用替代选择排序(replacement selection)并通过两次多路归并(multi-way merge)来合并文件时,最大文件的预期大小是多少?请解释你是如何得出这个答案的。(6分)
解答:
(a) 外部排序的两个阶段的主要任务:
第一阶段:
第一阶段的任务是将文件分割成较大的初始运行(runs),通过替代选择(replacement selection)方法生成这些运行。替代选择通过在内存中选择合适的元素来生成局部有序的运行,直到文件中的所有数据都被处理完。第二阶段:
第二阶段是将这些初始的运行合并成一个单一的有序运行文件。这是通过多路归并(multi-way merge)来完成的,多个运行同时被合并,直到最终得到一个完整的有序文件。
(b) 最大文件的预期大小计算:
工作内存大小:
工作内存为 256 KB,每个块大小为 8192 字节(8 KB),因此工作内存可以容纳 $ = 32 $ 个块。第一阶段:
替代选择生成的初始运行(run)的长度取决于内存的大小。假设每个块都能容纳一个元素,因此初始的运行长度为 32 块。由于每次替代选择都会生成一个有序的运行,因此每个运行大约为 512 KB。第二阶段:
通过第一次多路归并,32 个初始运行会被合并成更大的运行。每次多路归并将运行合并成长度为: $ 512 = 16 $然后,第二次多路归并将这些更大的运行再次合并。每次合并的长度为: $ 16 = 512 $
因此,最大文件的预期大小为 512MB。
解释:
第一阶段生成的运行: 替代选择排序生成的运行长度由内存大小决定。每个运行的大小与内存中可以存放的块数成正比,因此第一次生成的运行大约为 512 KB。
多路归并: 第一次多路归并将 32 个初始运行合并成一个长度为 16 MB 的运行。第二次归并将这些较大的运行合并成一个大小为 512 MB 的运行。





