图的基本应用

【深基18.例3】查找文献

题目描述

小 K 喜欢翻看洛谷博客获取知识。每篇文章可能会有若干个（也有可能没有）参考文献的链接指向别的博客文章。小 K 求知欲旺盛，如果他看了某篇文章，那么他一定会去看这篇文章的参考文献（如果他之前已经看过这篇参考文献的话就不用再看它了）。

假设洛谷博客里面一共有 $n(n\le10^5)$ 篇文章（编号为 1 到 $n$）以及 $m(m\le10^6)$ 条参考文献引用关系。目前小 K 已经打开了编号为 1 的一篇文章，请帮助小 K 设计一种方法，使小 K 可以不重复、不遗漏的看完所有他能看到的文章。

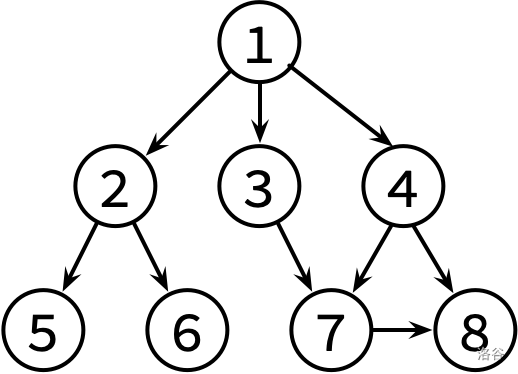
这边是已经整理好的参考文献关系图，其中，文献 X → Y 表示文章 X 有参考文献 Y。不保证编号为 1 的文章没有被其他文章引用。

请对这个图分别进行 DFS 和 BFS，并输出遍历结果。如果有很多篇文章可以参阅，请先看编号较小的那篇(因此你可能需要先排序)。

输入格式

共 $m+1$ 行，第 1 行为 2 个数，$n$ 和 $m$，分别表示一共有 $n(n\le10^5)$ 篇文章（编号为 1 到 $n$）以及$m(m\le10^6)$ 条参考文献引用关系。

接下来 $m$ 行，每行有两个整数 $X,Y$ 表示文章 X 有参考文献 Y。

输出格式

共 2 行。第一行为 DFS 遍历结果，第二行为 BFS 遍历结果。

样例 #1

样例输入 #1

样例输出 #1

1 2	1 2 5 6 3 7 8 4 1 2 3 4 5 6 7 8

给你一张有向图，要你把它深度遍历一遍再广度遍历一遍。
#include<iostream>
#include<algorithm>
#include<string>
#include<vector>
#include<cstring>
#include<queue>

using namespace std;
vector< int >g[1000000];
bool visit[10000000];
int n, m;
int u, v;
void dfs(int x, int cur)
{
	visit[x] = 1;
	cout << x<<" ";
	if (cur==n)
	{
		return;
	}
	for (int i = 0; i < g[x].size(); i++)
	{
		if (!visit[g[x][i]])
		{
			dfs(g[x][i], cur + 1);
		}
	}
}
queue<int>q;
void bfs(int x)
{
	memset(visit, 0, sizeof(visit));
	visit[x] = 1;
	q.push(x);
	while (!q.empty())
	{
		int v = q.front();
		q.pop();
		cout << v << ' ';
		for (int i = 0; i < g[v].size(); i++)
		{
			if (!visit[g[v][i]])
			{
				visit[g[v][i]] = 1;
				q.push(g[v][i]);
			}
		}
	}
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <=m ; i++)
	{
		cin >> u >> v;
		g[u].push_back(v);
	}
	for (int i = 1; i <=n ; i++)
	{
		sort(g[i].begin(), g[i].end());
	}
	dfs(1, 0);
	cout << '\n';
	bfs(1);
	return 0;
}

图的遍历

题目描述

给出 $N$ 个点，$M$ 条边的有向图，对于每个点 $v$，求 $A(v)$ 表示从点 $v$ 出发，能到达的编号最大的点。

输入格式

第 $1$ 行 $2$ 个整数 $N,M$，表示点数和边数。

接下来 $M$ 行，每行 $2$ 个整数 $U_i,V_i$，表示边 $(U_i,V_i)$。点用 $1,2,\dots,N$ 编号。

输出格式

一行 $N$ 个整数 $A(1),A(2),\dots,A(N)$。

样例 #1

样例输入 #1

样例输出 #1

4 4 3 4

提示

对于 $60\%$ 的数据，$1 \leq N,M \leq 10^3$。
对于 $100\%$ 的数据，$1 \leq N,M \leq 10^5$。

//反向存边，看看能到哪
#include<iostream>
#include<algorithm>
#include<string>
#include<vector>
using namespace std;
int n, m;
int u, v;
vector< int >g[1000000];
int a[10000000];
void dfs(int x, int d)
{
	if (a[x])
	{
		return;
	}
	a[x] = d;
	for (int i = 0; i < g[x].size(); i++)
	{
		dfs(g[x][i], d);
	}
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <=m ; i++)
	{
		cin >> u >> v;
		g[v].push_back(u);
        //反向存边
	}
	for (int i = n; i>=1  ; i--)
	{
		dfs(i, i);
	}//反向遍历
	for (int i = 1; i <=n ; i++)
	{
		cout << a[i] << ' ';
	}
}


//邻接表写法
    #include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 100010;
int n, m, head[N], cnt, ans[N];
struct node{
	int nxt, to;
}e[N];

void add(int x, int y) {
	e[++cnt].nxt = head[x];
	e[cnt].to = y;
	head[x] = cnt;
    //三板斧
}
void dfs(int x, int fa) {
	ans[x] = fa;
	for(int i = head[x]; i; i = e[i].nxt)
		if(!ans[e[i].to]) dfs(e[i].to, fa);
    //邻接表的遍历，一贯如此
}
int main() {
cin>>n>>m;
	for(int i = 1; i <= m; i++) {
cin>>x>>y;
		add(y, x);
	}
	for(int i = n; i >= 1; i--) {
		if(ans[i]) continue;
		dfs(i, i);
	}
	for(int i = 1; i <= n; i++) cout<<ans[i]<<" ";
	return 0;
}

【模板】拓扑排序 / 家谱树

题目描述

有个人的家族很大，辈分关系很混乱，请你帮整理一下这种关系。给出每个人的后代的信息。输出一个序列，使得每个人的后辈都比那个人后列出。

输入格式

第 1 行一个整数 N（1 N ），表示家族的人数。接下来 N 行，第 i 行描述第 i 个人的后代编号 a_{i,j}，表示 a_{i,j} 是 i 的后代。每行最后是 0 表示描述完毕。

输出格式

输出一个序列，使得每个人的后辈都比那个人后列出。如果有多种不同的序列，输出任意一种即可。

样例 #1

样例输入 #1

样例输出 #1

2 4 5 3 1

在解决下面一道题之前来个模板

//by dpcc
//世间温柔
//不过是芳春柳摇染花香
//槐序蝉鸣入深巷
//白茂叶落醉故乡
#include<bits/stdc++.h>
using namespace std;
using ll=long long ;
#define re register
#define in inline
#define rep(i,a,n)  for(re int i=a;i<=n;i++)
#define frep(i,a,n) for(re int i=a;i>=n;i--)
int n;
vector<int>a[110];
int du[110];
int b[110];
int n2;
inline void bfs()
{
	queue<int>q;
rep(i,1,n)
{
	if(!du[i])
{
	q.push(i);
	}
		}			
while(!q.empty())
{
	int x=q.front();
	b[++n2]=x;
	q.pop();
	int t=a[x].size()-1;
	rep(i,0,t)
	{
	du[a[x][i]]--;
	if(!du[a[x][i]])
	{
		q.push(a[x][i]);
	}
	}	
}	
frep(i,n2,1)
{
	cout<<b[i]<<' ';
}
}
signed main()
{
cin>>n;
rep(i,1,n)
{
	int t;
	cin>>t;
	while(t!=0)
	{
	a[t].push_back(i);
		du[i]++;
		cin>>t;
	}
	}		
bfs();
return 0;
}

杂务

题目描述

John 的农场在给奶牛挤奶前有很多杂务要完成，每一项杂务都需要一定的时间来完成它。比如：他们要将奶牛集合起来，将他们赶进牛棚，为奶牛清洗乳房以及一些其它工作。尽早将所有杂务完成是必要的，因为这样才有更多时间挤出更多的牛奶。

当然，有些杂务必须在另一些杂务完成的情况下才能进行。比如：只有将奶牛赶进牛棚才能开始为它清洗乳房，还有在未给奶牛清洗乳房之前不能挤奶。我们把这些工作称为完成本项工作的准备工作。至少有一项杂务不要求有准备工作，这个可以最早着手完成的工作，标记为杂务 $1$。

John 有需要完成的 $n$ 个杂务的清单，并且这份清单是有一定顺序的，杂务 $k\ (k>1)$ 的准备工作只可能在杂务 $1$ 至 $k-1$ 中。

写一个程序依次读入每个杂务的工作说明。计算出所有杂务都被完成的最短时间。当然互相没有关系的杂务可以同时工作，并且，你可以假定 John 的农场有足够多的工人来同时完成任意多项任务。

输入格式

第1行：一个整数 $n\ (3 \le n \le 10{,}000)$，必须完成的杂务的数目；

第 $2$ 至 $n+1$ 行，每行有一些用空格隔开的整数，分别表示：

工作序号（保证在输入文件中是从 $1$ 到 $n$ 有序递增的）；
完成工作所需要的时间 $len\ (1 \le len \le 100)$；
一些必须完成的准备工作，总数不超过 $100$ 个，由一个数字 $0$ 结束。有些杂务没有需要准备的工作只描述一个单独的 $0$。

保证整个输入文件中不会出现多余的空格。

输出格式

一个整数，表示完成所有杂务所需的最短时间。

样例 #1

样例输入 #1

7
1 5 0
2 2 1 0
3 3 2 0
4 6 1 0
5 1 2 4 0
6 8 2 4 0
7 4 3 5 6 0

样例输出 #1

#include<iostream>
#include<bits/stdc++.h>
using namespace std;
const int N=100000;
int ind[N];
int f[N];
int a[N];
vector<int>edge[N];
queue<int>q;
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
	int x;
	cin>>x;
	cin>>a[i];
	int y;
	while(cin>>y&&y)
	{
		edge[y].push_back(x);
		ind[x]++;	
        //入度
	}	
	}	
	for(int i=1;i<=n;i++)
	{
		if(ind[i]==0)
		{
			q.push(i);
		}
		f[i]=a[i];	
	}
	while(!q.empty())
{
	int p=q.front();
	q.pop();
	for(int i=0;i<edge[p].size();i++)
	{
		int u=edge[p][i];
		ind[u]--;
		if(ind[u]==0)
		{
			q.push(u);
		}
		f[u]=max(f[u],f[p]+a[u]);		
	}
	}	
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		ans=max(ans,f[i]);	
	}
	cout<<ans;	
}

/*
此种拓扑排序共有四个主要步骤：
初始化队列，将入度为 0的节点放入队列。
取出队首，遍历其出边，将能够到达的点入度减一，同时维护答案数组。
若在此时一个点的入度变为 0，那么将其加入队列。
回到第二步，直到队列为空。
*/

最大食物链计数

题目背景

你知道食物链吗？Delia 生物考试的时候，数食物链条数的题目全都错了，因为她总是重复数了几条或漏掉了几条。于是她来就来求助你，然而你也不会啊！写一个程序来帮帮她吧。

题目描述

给你一个食物网，你要求出这个食物网中最大食物链的数量。

（这里的“最大食物链”，指的是生物学意义上的食物链，即最左端是不会捕食其他生物的生产者，最右端是不会被其他生物捕食的消费者。）

Delia 非常急，所以你只有 $1$ 秒的时间。

由于这个结果可能过大，你只需要输出总数模上 $80112002$ 的结果。

输入格式

第一行，两个正整数 $n、m$，表示生物种类 $n$ 和吃与被吃的关系数 $m$。

接下来 $m$ 行，每行两个正整数，表示被吃的生物A和吃A的生物B。

输出格式

一行一个整数，为最大食物链数量模上 $80112002$ 的结果。

样例 #1

样例输入 #1

样例输出 #1

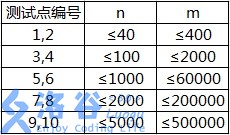
提示

各测试点满足以下约定：

【补充说明】

数据中不会出现环，满足生物学的要求。（感谢 @AKEE ）

/*
想要找到一条 最大食物链 ，那么这条路径的 起点 入度要为0，终点 出度要为0。 故：

记录入度，记录出度


*/
#include<bits/stdc++.h>
using namespace std;
int n,m,ru[5005],chu[5005],a,b,f[5005],ans;
int mp[5005][5005];
queue<int> q;
int main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
	cin>>a>>b;
		mp[a][b]=1;//a-b有一条路径，才5000，邻接矩阵绰绰有余
		chu[a]++;
		ru[b]++;
	}
	for(int i=1;i<=n;i++){
		if(ru[i]==0) {
			f[i]=1;
			q.push(i);
		}
	}
	while(!q.empty()){
		int a=q.front();
		q.pop();
		for(int k=1;k<=n;k++){
			if(mp[a][k]==0)continue;
			f[k]+=f[a];
			f[k]%=80112002;
			ru[k]--;
			if(ru[k]==0){
				if(chu[k]==0){
					ans+=f[k];//到达食物链顶端咯
					ans%=80112002;
                 
				}
				q.push(k);
			}
		}
	}
	cout<<ans; 
}

最长路

题目描述

设 $G$ 为有 $n$ 个顶点的带权有向无环图，$G$ 中各顶点的编号为 $1$ 到 $n$，请设计算法，计算图 $G$ 中 $1, n$ 间的最长路径。

输入格式

输入的第一行有两个整数，分别代表图的点数 $n$ 和边数 $m$。

第 $2$ 到第 $(m + 1)$ 行，每行 $3$ 个整数 $u, v, w$（$u<v$），代表存在一条从 $u$ 到 $v$ 边权为 $w$ 的边。

输出格式

输出一行一个整数，代表 $1$ 到 $n$ 的最长路。

若 $1$ 无法到达 $n$，请输出 $-1$。

样例 #1

样例输入 #1

1
2

2 1
1 2 1

样例输出 #1

提示

【数据规模与约定】

对于 $20\%$的数据，$n \leq 100$，$m \leq 10^3$。
对于 $40\%$ 的数据，$n \leq 10^3$，$m \leq 10^{4}$。
对于 $100\%$ 的数据，$1 \leq n \leq 1500$，$0 \leq m \leq 5 \times 10^4$，$1 \leq u, v \leq n$，$-10^5 \leq w \leq 10^5$。

//直接floyd+邻接矩阵就水过去了（）
#include<bits/stdc++.h>
using namespace std;
int n,m,x,y,z;
#define INF 0x3f3f3f
int mp[2000][2000];
int main()
{
	cin>>n>>m;
	for(int i=0;i<n;i++)
	{
		for(int j=0;j<n;j++)
		{
			if(i==j)
			
			{
				mp[i][j]=0;
			}
			else{
				mp[i][j]=INF;
			}
		}	
	}
	for(int i=0;i<m;i++)
	{
	cin>>x>>y>>z;
	x--;y--;
	mp[x][y]=min(mp[x][y],-z);
	
	}	
	for(int k=0;k<n;k++)
	{
		for(int i=0;i<n;i++)
		{
			for(int j=0;j<n;j++)
			{
				if(mp[i][k]!=INF&&mp[k][j]!=INF)
				{
					mp[i][j]=min(mp[i][j],mp[i][k]+mp[k][j]);
				}
				
			}
		}	
	}
	if(mp[0][n-1]==INF)
	{
		cout<<-1;
	}else{
		cout<<-mp[0][n-1];
			}	
}


//题解这个应该算正解了
//喵喵喵（妙）
#include<bits/stdc++.h>
using namespace std;
int n,m,in[1505];//存入度数量
vector<int>g[1505];//存边
vector<int>d[1505];//存边权
queue<int>q;//队列
int v[1505];//存最长路
int main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		int ff,tt,dd;
		cin>>ff>>tt>>dd;
		g[ff].push_back(tt);
        //点
		d[ff].push_back(dd);
        //权
		in[tt]++;
	}
	for(int i=2;i<=n;i++)
	{
		v[i]=-1e9;
		if(!in[i]) q.push(i);
	}//初始化
	while(!q.empty())
	{
		int x=q.front();
		q.pop();
		for(int i=0;i<g[x].size();i++)
			if(!--in[g[x][i]]) q.push(g[x][i]);
	}
	//废弃其他的入度为0的点。
    //这一步是关键
	q.push(1);
	while(!q.empty())
	{
		int x=q.front();
		q.pop();
		for(int i=0;i<g[x].size();i++)
		{
			if(v[g[x][i]]<v[x]+d[x][i]) v[g[x][i]]=v[x]+d[x][i];//松弛
			if(!--in[g[x][i]]) q.push(g[x][i]);//如果入度为0就加入队列
		}
	}
	if(v[n]==-1e9) cout<<"-1";
	else cout<<v[n];//输出结果
	return 0;
}

词链

题目描述

如果单词 $X$ 的末字母与单词 $Y$ 的首字母相同，则 $X$ 与 $Y$ 可以相连成 $X.Y$。（注意：$X$、$Y$ 之间是英文的句号 .）。例如，单词 dog 与单词 gopher，则 dog 与 gopher 可以相连成 dog.gopher。

另外还有一些例子： - dog.gopher - gopher.rat - rat.tiger - aloha.aloha - arachnid.dog

连接成的词可以与其他单词相连，组成更长的词链，例如：

aloha.arachnid.dog.gopher.rat.tiger

注意到，. 两边的字母一定是相同的。

现在给你一些单词，请你找到字典序最小的词链，使得每个单词在词链中出现且仅出现一次。注意，相同的单词若出现了 $k$ 次就需要输出 $k$ 次。

输入格式

第一行是一个正整数 $n$（$1 \le n \le 1000$），代表单词数量。

接下来共有 $n$ 行，每行是一个由 $1$ 到 $20$ 个小写字母组成的单词。

输出格式

只有一行，表示组成字典序最小的词链，若不存在则只输出三个星号 ***。

样例 #1

样例输入 #1

6
aloha
arachnid
dog
gopher
rat
tiger

样例输出 #1

1	aloha.arachnid.dog.gopher.rat.tiger

提示

对于 $40\%$ 的数据，有 $n \leq 10$；
对于 $100\%$ 的数据，有 $n \leq 1000$。

#include<bits/stdc++.h>
using namespace std;
int n;
const int N=1001;
string a[N];
vector<int> e[N];
int ind[N];
int rnd[N];
bool used[N];
void dfs(int s, string curr, int count) {
if (count == n) {
		curr[curr.length() - 1] = ' '; 
		cout << curr;
		exit(0);
    //相当于return 0
	}
	for (auto i : e[s])
		if (!used[i]) {
			used[i] = 1;
			dfs(i, curr + a[i] + '.', count + 1);
			used[i] = 0;
		}
}

int main() {
cin >> n;
	for (int i = 1; i <= n; ++i) {
	cin >> a[i];
		++ind[a[i][0]];
        //首字母++
		++rnd[a[i][a[i].length() - 1]];
        //尾字母++
	}
	sort(a + 1, a + n + 1);
    //排序
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= n; ++j)
			if (i != j && a[i][a[i].length() - 1] == a[j][0])
				e[i].push_back(j);
    //存边，如果首尾相接，可以存边
	for (int i = 1; i <= n; ++i)
		if (ind[a[i][0]] == rnd[a[i][0]] + 1) 
        {
            //寻找起始点的过程
            //因为首字母=尾字母出现加一
			used[i] = 1;
			dfs(i, a[i] + '.', 1);
			used[i] = 0;
		}
	used[1] = 1;
	dfs(1, a[1] + '.', 1);
	used[1] = 0;
	cout << "***";
	
}

[USACO06DEC] Cow Picnic S

题目描述

The cows are having a picnic! Each of Farmer John's K (1 ≤ K ≤ 100) cows is grazing in one of N (1 ≤ N ≤ 1,000) pastures, conveniently numbered 1...N. The pastures are connected by M (1 ≤ M ≤ 10,000) one-way paths (no path connects a pasture to itself).

The cows want to gather in the same pasture for their picnic, but (because of the one-way paths) some cows may only be able to get to some pastures. Help the cows out by figuring out how many pastures are reachable by all cows, and hence are possible picnic locations.

$K(1 \le K \le 100)$ 只奶牛分散在 $N(1 \le N \le 1000)$ 个牧场．现在她们要集中起来进餐。牧场之间有 $M(1 \le M \le 10000)$ 条有向路连接，而且不存在起点和终点相同的有向路．她们进餐的地点必须是所有奶牛都可到达的地方。那么，有多少这样的牧场可供进食呢？

输入格式

Line 1: Three space-separated integers, respectively: K, N, and M

Lines 2..K+1: Line i+1 contains a single integer (1..N) which is the number of the pasture in which cow i is grazing.

Lines K+2..M+K+1: Each line contains two space-separated integers, respectively A and B (both 1..N and A != B), representing a one-way path from pasture A to pasture B.

输出格式

Line 1: The single integer that is the number of pastures that are reachable by all cows via the one-way paths.

样例 #1

样例输入 #1

样例输出 #1

提示

The cows can meet in pastures 3 or 4.

//从k个奶牛分别dfs，用mk[i]表示第i个牧场被遍历过多少次，最后只有mk[i]==k的牧场满足条件。无权的有向图也可以用vector存储。
#include<bits/stdc++.h>
using namespace std;
bool vis[10000];
int k,n,m,ans;
int mk[10000];
int a[10000];
vector<int>b[10000];
void dfs(int x)
{
	vis[x]=1;
	mk[x]++;
	for(int i=0;i<b[x].size();i++)
	{
		if(!vis[b[x][i]])
		{
			dfs(b[x][i]);
		}	
	}	
}
int main()
{
	int x,y;
	cin>>k>>n>>m;
	for(int i=1;i<=k;i++)
	{
		cin>>a[i];
	}
	for(int i=1;i<=m;i++)
	{
		cin>>x>>y;
		b[x].push_back(y);
	}
	for(int i=1;i<=k;i++)
{
	for(int j=1;j<=n;j++)
	{
		vis[j]=0;
	}
	dfs(a[i]);	
}
	for(int i=1;i<=n;i++)
	{
		if(mk[i]==k)
		{
			ans++;
		}		
	}
	cout<<ans;	
}

幻象迷宫

题目背景

（喵星人 LHX 和 WD 同心协力击退了汪星人的入侵，不幸的是，汪星人撤退之前给它们制造了一片幻象迷宫。）

WD：呜呜，肿么办啊……

LHX：momo...我们一定能走出去的！

WD：嗯，+U+U！

题目描述

幻象迷宫可以认为是无限大的，不过它由若干个 $N\times M$ 的矩阵重复组成。矩阵中有的地方是道路，用 $\verb!.!$ 表示；有的地方是墙，用 $\verb!#!$ 表示。LHX 和 WD 所在的位置用 $\verb!S!$ 表示。也就是对于迷宫中的一个点$(x,y)$，如果 $(x \bmod n,y \bmod m)$ 是 $\verb!.!$ 或者 $\verb!S!$，那么这个地方是道路；如果 $(x \bmod n,y \bmod m)$ 是$\verb!#!$，那么这个地方是墙。LHX 和 WD 可以向上下左右四个方向移动，当然不能移动到墙上。

请你告诉 LHX 和 WD，它们能否走出幻象迷宫（如果它们能走到距离起点无限远处，就认为能走出去）。如果不能的话，LHX 就只好启动城堡的毁灭程序了……当然不到万不得已，他不想这么做。

输入格式

输入包含多组数据，以 EOF 结尾。

每组数据的第一行是两个整数 $N,M$。

接下来是一个 $N\times M$ 的字符矩阵，表示迷宫里 $(0,0)$ 到 $(n-1,m-1)$ 这个矩阵单元。

输出格式

对于每组数据，输出一个字符串，Yes 或者 No。

样例 #1

样例输入 #1

5 4
##.#
##S#
#..#
#.##
#..#
5 4
##.#
##S#
#..#
..#.
#.##

样例输出 #1

1
2

Yes
No

提示

对于 $30\%$ 的数据，$1\le N,M\le 20$；
对于 $50\%$ 的数据，$1\le N,M\le 100$；
对于 $100\%$ 的数据，$1\le N,M\le 1500$，每个测试点不超过 $10$ 组数据。

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 1500 + 1;
int dx[4] = {1, -1, 0, 0};
 int dy[4] = {0, 0, 1, -1};
int n, m;
int st_x, st_y;
int vis[MAXN][MAXN][3];
bool fl, a[MAXN][MAXN];
char ch;

void dfs(int x, int y, int lx, int ly) {
    if(fl) return;
    if(vis[x][y][0] && (vis[x][y][1]!=lx || vis[x][y][2]!=ly)) {
        fl = 1;
        return;
        //成功标记
    }
    if (vis[x][y][0] && vis[x][y][1]==lx && vis[x][y][2]==ly) return;
    vis[x][y][1] = lx, vis[x][y][2] = ly, vis[x][y][0] = 1;
    //第二次走出迷宫了呢，也就是说能到更远的地方了
    for(int i=0; i<4; ++i) {
        int xx = (x + dx[i] + n) % n, yy = (y + dy[i] + m) % m;
        int lxx = lx + dx[i], lyy = ly + dy[i];
        if(!a[xx][yy]) 
        {  
                dfs(xx, yy, lxx, lyy);
        }
        //可以走就走罢
    }
}
int main() {

    while(cin >> n >> m) {
        fl = 0;
        memset(a, 0, sizeof(a));
        memset(vis, 0, sizeof(vis));
        //多组清零
        for(int i=0; i<n; ++i)
            for(int j=0; j<m; ++j) {
                cin >> ch;
                if(ch == '#') a[i][j] = 1;
                //标记
                if(ch == 'S') st_x = i, st_y = j;
                //起点
            }
        dfs(st_x, st_y, st_x, st_y);
        if(fl) puts("Yes");
        else puts("No");
    }
}

排序

题目描述

一个不同的值的升序排序数列指的是一个从左到右元素依次增大的序列，例如，一个有序的数列 $A,B,C,D$ 表示 $A<B,B<C,C<D$。在这道题中，我们将给你一系列形如 $A<B$ 的关系，并要求你判断是否能够根据这些关系确定这个数列的顺序。

输入格式

第一行有两个正整数 $n,m$，$n$ 表示需要排序的元素数量，$2\leq n\leq 26$，第 $1$ 到 $n$ 个元素将用大写的 $A,B,C,D,\dots$ 表示。$m$ 表示将给出的形如 $A<B$ 的关系的数量。

接下来有 $m$ 行，每行有 $3$ 个字符，分别为一个大写字母，一个 < 符号，一个大写字母，表示两个元素之间的关系。

输出格式

若根据前 $x$ 个关系即可确定这 $n$ 个元素的顺序 yyy..y（如 ABC），输出

Sorted sequence determined after xxx relations: yyy...y.

若根据前 $x$ 个关系即发现存在矛盾（如 $A<B,B<C,C<A$），输出

Inconsistency found after x relations.

若根据这 $m$ 个关系无法确定这 $n$ 个元素的顺序，输出

Sorted sequence cannot be determined.

（提示：确定 $n$ 个元素的顺序后即可结束程序，可以不用考虑确定顺序之后出现矛盾的情况）

样例 #1

样例输入 #1

4 6
A<B
A<C
B<C
C<D
B<D
A<B

样例输出 #1

1	Sorted sequence determined after 4 relations: ABCD.

样例 #2

样例输入 #2

1
2
3

3 2
A<B
B<A

样例输出 #2

1	Inconsistency found after 2 relations.

样例 #3

样例输入 #3

1
2

26 1
A<Z

样例输出 #3

1	Sorted sequence cannot be determined.

提示

$2 \leq n \leq 26,1 \leq m \leq 600$。

#include <bits/stdc++.h>
using namespace std;
const int N  = 30;
int n, m;
vector<int> e[N];
int degree[N];
int a[N];
stack<int> s;
bool vis[N];
int mrk;
bool topo(int r) 
{
	int sz = 0;
	bool finished = true;
	int t[N];
	for(int i = 0; i < n; i++)
    {
		t[i] = degree[i];
		if(!degree[i]) s.push(i), vis[i] = 1;
	}
    //记录，顺便找到入度为0的点
	while(!s.empty()) 
    {
		if(s.size() > 1) finished = 0;
        //这里说明最小有两个，无法确定
		int k = s.top();
		a[sz++] = k; 
		s.pop();
		for(int i = 0; i < e[k].size(); i++) t[e[k][i]]--;
		for(int i = 0; i < n; i++) if(!t[i] && !vis[i]) s.push(i), vis[i] = 1;
	}
	if(sz < n) return 0;
	if(finished && !mrk) mrk = r;
	return 1;
}

int main() {
	cin>>n>>m;
	for(int i = 1; i <= m; i++) 
    {
		string c;
		cin>>c;
		int x = c[0] - 'A', y = c[2] - 'A';
		e[x].push_back(y);
		degree[y]++;
		if(!topo(i))
        {
			cout<<"Inconsistency found after "<<i<<" relations.";
			return 0;
		}
		memset(vis, false, sizeof vis);
        if(mrk)
            //如果有了，其实已经确定了，就跳过罢
        {
            break;
		}
	}
	if(mrk) 
    {
		cout<<"Sorted sequence determined after "<<mrk<<" relations: ";
		for(int i = 0; i < n; i++) cout<<char(a[i] + 'A');
		cout<<".";
	}
	else cout<<"Sorted sequence cannot be determined.";
}

[NOIP2013 普及组] 车站分级

题目背景

NOIP2013 普及组 T4

题目描述

一条单向的铁路线上，依次有编号为 $1, 2, …, n$ 的 $n $ 个火车站。每个火车站都有一个级别，最低为 $1$ 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 $x$，则始发站、终点站之间所有级别大于等于火车站 $ x$ 的都必须停靠。
注意：起始站和终点站自然也算作事先已知需要停靠的站点。

例如，下表是 $ 5 $ 趟车次的运行情况。其中，前 $ 4$ 趟车次均满足要求，而第 $5$ 趟车次由于停靠了 $3$ 号火车站（$2$ 级）却未停靠途经的 $6$ 号火车站（亦为 $2$ 级）而不满足要求。

现有 $m$ 趟车次的运行情况（全部满足要求），试推算这 $ n$ 个火车站至少分为几个不同的级别。

输入格式

第一行包含 $2$ 个正整数 $n, m$，用一个空格隔开。

第 $i + 1$ 行 $(1 ≤ i ≤ m)$ 中，首先是一个正整数 $s_i\ (2 ≤ s_i ≤ n)$，表示第 $ i$ 趟车次有 $s_i$ 个停靠站；接下来有 $ s_i$ 个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出格式

一个正整数，即 $n$ 个火车站最少划分的级别数。

样例 #1

样例输入 #1

1
2
3

9 2 
4 1 3 5 6 
3 3 5 6

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

提示

对于 $ 20%$ 的数据，$1 ≤ n, m ≤ 10$；

对于 $50\%$ 的数据，$1 ≤ n, m ≤ 100$；

对于 $100\%$ 的数据，$1 ≤ n, m ≤ 1000$。

#include<bits/stdc++.h>
const int N=1005;
using namespace std;
int n,m,ans,st[N],s,tuopu[N][N],de[N],tt[N],top;
bool is[N],bo[N];		
int main() {
 	cin>>n>>m;
    for(int i=1;i<=m;i++) {
        memset(is,0,sizeof(is));
        //多组要重测，不过这个和一般的重测还不太一样
        cin>>s;
        //输入个数
        for(int j=1;j<=s;j++)
        {
            cin>>st[j];
            is[st[j]]=1;
            //标记一下，这个是比较大的
        }
        for(int j=st[1];j<=st[s];j++)
            //建边过程
            if(!is[j]2)			
                for(int k=1;k<=s;k++)	
                    if(!tuopu[j][st[k]]) 
                    {
                        tuopu[j][st[k]]=1;
                        //j<st[k]
                        de[st[k]]++;
                        //入度想做
                    }
    } 
    do
    {
        top=0;
        for(int i=1;i<=n;i++)
            if(de[i]==0&&!bo[i]) 
            {
                tt[++top]=i;
                //入度为0
                bo[i]=true;
            }
        for(int i=1;i<=top;i++)
            for(int j=1;j<=n;j++)
                if(tuopu[tt[i]][j])
                    //如果能到，弄成0
                {
                    tuopu[tt[i]][j]=0;
                    de[j]--;
                }
        ans++;
    } while(top);
    cout<<ans-1;
}