基础数学问题

进制转换

题目描述

请你编一程序实现两种不同进制之间的数据转换。

输入格式

共三行，第一行是一个正整数，表示需要转换的数的进制 $n\ (2\le n\le 16)$，第二行是一个 $n$ 进制数，若 $n>10$ 则用大写字母 $\verb!A!\sim \verb!F!$ 表示数码 $10\sim 15$，并且该 $n$ 进制数对应的十进制的值不超过 $10^9$，第三行也是一个正整数，表示转换之后的数的进制 $m\ (2\le m\le 16)$。

输出格式

一个正整数，表示转换之后的 $m$ 进制数。

样例 #1

样例输入 #1

1
2
3

16
FF
2

样例输出 #1

11111111

/*
上公式即可
*/
#include<bits/stdc++.h>
using namespace std;
string a;
int c[10000000],d,e,f,g,sum,ans;
int main()
{
  cin>>d;
    cin>>a;
    cin>>f;
    for(int x=0;x<a.size();x++)
    {
        if(a[x]<'A'){
            e=pow(d,a.size()-x-1);
            e*=(a[x]-'0');
            sum+=e;
        }
        else
        {
            e=pow(d,a.size()-1-x);
            e*=(a[x]-'A'+10);
            sum+=e;
        }
    }
        while(sum>0)
        {
        c[g++]=sum%f;
        sum/=f;
    }
    for(int x=g-1;x>=0;x--)
    {
        if(c[x]>=10)  cout<<char(c[x]+'A'-10);
        else cout<<c[x];
    }

}

找筷子

题目描述

经过一段时间的紧张筹备，电脑小组的“RP 餐厅”终于开业了，这天，经理 LXC 接到了一个定餐大单，可把大家乐坏了！员工们齐心协力按要求准备好了套餐正准备派送时，突然碰到一个棘手的问题:筷子！

CX 小朋友找出了餐厅中所有的筷子，但遗憾的是这些筷子长短不一，而我们都知道筷子需要长度一样的才能组成一双，更麻烦的是 CX 找出来的这些筷子数量为奇数，但是巧合的是，这些筷子中只有一只筷子是落单的，其余都成双，善良的你，可以帮 CX 找出这只落单的筷子的长度吗？

输入格式

第一行是一个整数，表示筷子的数量 $n$。

第二行有 $n$ 个整数，第 $i$ 个整数表示第 $i$ 根筷子的长度 $a_i$。

输出格式

输出一行一个整数表示答案。

样例 #1

样例输入 #1

1 2	9 2 2 1 3 3 3 2 3 1

样例输出 #1

提示

数据规模与约定

对于 $30\%$ 的数据，保证 $n \leq 10^5$。
对于 $100\%$ 的数据，保证 $1 \leq n \leq 10^7 + 1$，$1 \leq a_i \leq 10^9$。

提示

请注意数据读入对程序效率造成的影响。
请注意本题的空间限制为 $4$ Mb。

#include<iostream>
using namespace std;
int x,n,ans;
int main(){
   ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++) 
    {
        cin>>x;
        ans^=x;
    }
cout<<ans;
}

高低位交换

题目描述

给出一个小于 $2^{32}$ 的非负整数。这个数可以用一个 $32$ 位的二进制数表示（不足 $32$ 位用 $0$ 补足）。我们称这个二进制数的前 $16$ 位为“高位”，后 $16$ 位为“低位”。将它的高低位交换，我们可以得到一个新的数。试问这个新的数是多少（用十进制表示）。

例如，数 $1314520$ 用二进制表示为 $0000\,0000\,0001\,0100\,0000\,1110\,1101\,1000$（添加了 $11$ 个前导 $0$ 补足为 $32$ 位），其中前 $16$ 位为高位，即 $0000\,0000\,0001\,0100$；后 $16$ 位为低位，即 $0000\,1110\,1101\,1000$。将它的高低位进行交换，我们得到了一个新的二进制数 $0000\,1110\,1101\,1000\,0000\,0000\,0001\,0100$。它即是十进制的 $249036820$。

输入格式

一个小于 $2^{32}$ 的非负整数

输出格式

将新的数输出

样例 #1

样例输入 #1

样例输出 #1

249036820

#include<iostream>
using namespace std;
int main()
{
	unsigned int n;
	cin >> n;
	cout << (n >> 16) + (n << 16);
	return 0;


}

[NOIP2000 提高组] 进制转换

题目背景

NOIP2000 提高组 T1

题目描述

我们可以用这样的方式来表示一个十进制数：将每个阿拉伯数字乘以一个以该数字所处位置为指数，以 $10$ 为底数的幂之和的形式。例如 $123$ 可表示为 $1 \times 10^2+2\times 10^1+3\times 10^0$ 这样的形式。

与之相似的，对二进制数来说，也可表示成每个二进制数码乘以一个以该数字所处位置为指数，以 $2$ 为底数的幂之和的形式。

一般说来，任何一个正整数 $R$ 或一个负整数 $-R$ 都可以被选来作为一个数制系统的基数。如果是以 $R$ 或 $-R$ 为基数，则需要用到的数码为 $0,1,\dots,R-1$。

例如当 $R=7$ 时,所需用到的数码是 $0,1,2,3,4,5,6$，这与其是 $R$ 或 $-R$ 无关。如果作为基数的数绝对值超过 $10$，则为了表示这些数码，通常使用英文字母来表示那些大于 $9$ 的数码。例如对 $16$ 进制数来说,用 $A$ 表示 $10$，用 $B$ 表示 $11$，用 $C$ 表示 $12$，以此类推。

在负进制数中是用 $-R $ 作为基数，例如 $-15$（十进制）相当于 $(110001)_{-2}$（$-2$进制），并且它可以被表示为 $2$ 的幂级数的和数：

\[(110001)_{-2}=1\times (-2)^5+1\times (-2)^4+0\times (-2)^3+0\times (-2)^2+0\times (-2)^1 +1\times (-2)^0\]

设计一个程序，读入一个十进制数和一个负进制数的基数，并将此十进制数转换为此负进制下的数。

输入格式

输入的每行有两个输入数据。

第一个是十进制数 $n$。第二个是负进制数的基数 $R$。

输出格式

输出此负进制数及其基数，若此基数超过 $10$，则参照 $16$ 进制的方式处理。

样例 #1

样例输入 #1

30000 -2

样例输出 #1

1	30000=11011010101110000(base-2)

样例 #2

样例输入 #2

-20000 -2

样例输出 #2

1	-20000=1111011000100000(base-2)

样例 #3

样例输入 #3

28800 -16

样例输出 #3

1	28800=19180(base-16)

样例 #4

样例输入 #4

1	-25000 -16

样例输出 #4

1	-25000=7FB8(base-16)

提示

数据范围

对于 $100\%$ 的数据，$-20 \le R \le -2$，$|n| \le 37336$。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
void zhuan(int n,int r)
{
	if(n==0) return ;
	int m=n%r;
	if(m<0) m-=r,n+=r;
    //处理负数的过程
	if(m>=10) m='A'+m-10;
	else m+='0';	
	zhuan(n/r,r);	
	cout<<m;
	return ;
}
int main()
{

	int n,r;
	cin>>n>>r;
	cout<<n<<"=";
	zhuan(n,r);
cout<<"(base"<<r<<")";

}

编号

题目描述

太郎有 $N$ 只兔子，现在为了方便识别它们，太郎要给他们编号。兔子们向太郎表达了它们对号码的喜好，每个兔子 $i$ 想要一个整数，介于 $1$ 和 $M_i$ 之间（可以为 $1$ 或 $M_i$）。当然，每个兔子的编号是不同的。现在太郎想知道一共有多少种编号的方法。

你只用输出答案对 $10^9+7$ 取余的结果即可。如果这是不可能的，就输出 $0$。

输入格式

第一行是一个整数 $N$。

第二行 $N$ 个整数 $M_i$。

输出格式

一个整数，表示方案总数。

样例 #1

样例输入 #1

1
2

2
5 8

样例输出 #1

提示

数据范围及约定

对于全部数据，$1 \le N \le 50$，$1\le M_i\le 1000$。

#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
    int n,i,maxnumber[51]; long long ans=1; cin>>n;
    for(i=1;i<=n;i++)cin>>maxnumber[i];
    sort(maxnumber+1,maxnumber+n+1); 
    for(i=1;i<=n;i++){ans*=(maxnumber[i]-i+1); ans%=1000000007;} 
    cout<<ans;
}

[NOIP2016 提高组] 组合数问题

题目背景

NOIP2016 提高组 D2T1

题目描述

组合数 $\binom{n}{m}$ 表示的是从 $n$ 个物品中选出 $m$ 个物品的方案数。举个例子，从 $(1,2,3)$ 三个物品中选择两个物品可以有 $(1,2),(1,3),(2,3)$ 这三种选择方法。根据组合数的定义，我们可以给出计算组合数 $\binom{n}{m}$ 的一般公式：

\[\binom{n}{m}=\frac{n!}{m!(n-m)!}\]

其中 $n!=1\times2\times\cdots\times n$；特别地，定义 $0!=1$。

小葱想知道如果给定 $n,m$ 和 $k$，对于所有的 $0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )$ 有多少对 $(i,j)$ 满足 $k\mid\binom{i}{j}$。

输入格式

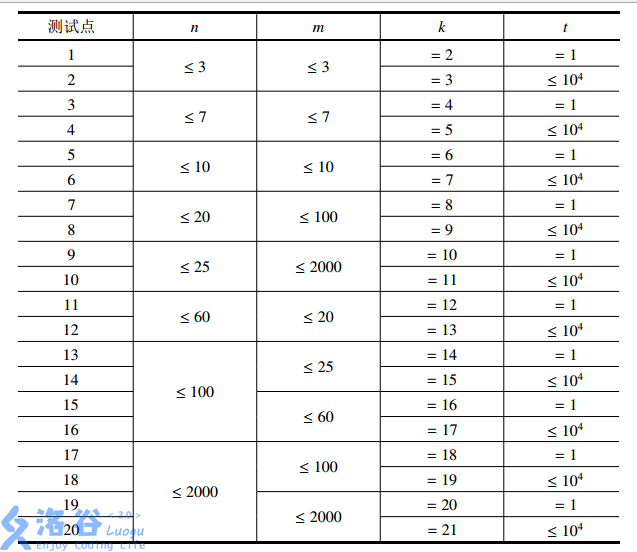
第一行有两个整数 $t,k$，其中 $t$ 代表该测试点总共有多少组测试数据，$k$ 的意义见问题描述。

接下来 $t$ 行每行两个整数 $n,m$，其中 $n,m$ 的意义见问题描述。

输出格式

共 $t$ 行，每行一个整数代表所有的 $0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )$ 中有多少对 $(i,j)$ 满足 $k\mid\binom{i}{j}$。

样例 #1

样例输入 #1

1
2

1 2
3 3

样例输出 #1

样例 #2

样例输入 #2

1
2
3

2 5
4 5
6 7

样例输出 #2

1
2

0
7

提示

【样例1说明】

在所有可能的情况中，只有 $\binom{2}{1} = 2$ 一种情况是 $2$ 的倍数。

【子任务】

对于全部的测试点，保证 $0 \leq n, m \leq 2 \times 10^3$，$1 \leq t \leq 10^4$。

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int t,k,n,m;
int c[2005][2005],s[2005][2005];
void prepare()
{
    c[1][1]=1;
    for(int i=0;i<=2000;i++) c[i][0]=1;
    for(int i=1;i<=2000;i++)
    {
        for(int j=1;j<=i;j++)
        {
            c[i][j]=(c[i-1][j]+c[i-1][j-1])%k;
        }
    }
    //预处理出杨辉三角的模数
    for(int i=2;i<=2000;i++){
        for(int j=1;j<=i;j++){
            s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
            if(c[i][j]==0) s[i][j]+=1;
        }
          s[i][i+1]=s[i][i];
       //前缀和
    }
}
int main()
{
    memset(c,0,sizeof(c));
    memset(s,0,sizeof(s));
    cin>>t>>k;
    prepare();
    while(t--){
        cin>>n>>m;
        if(m>n) m=n;
        cout<<s[n][m]<<'\n';
    }    
    return 0;
}

直线交点数

题目描述

假设平面上有 $N$ 条直线，且无三线共点，那么这些直线一共能有多少不同的交点数？

输入格式

一行，一个整数 $N$，代表有 $N$ 条直线。

输出格式

一行，一个整数，表示方案总数。

样例 #1

样例输入 #1

样例输出 #1

提示

对于所有数据，满足 $1 \le N \le 25$。

#include<bits/stdc++.h>
using namespace std;
int n,ans=0;bool f[10010];
void s(int p,int m)
{
        if(p==0) 
        {
            if(!f[m]) 
            ans++; 
            f[m]=1;
        }
        else 
        {
            for(int r=p;r>=1;r--) 
            {
                s(p-r,r*(p-r)+m);
                /*
                第一个参数是我们当前的直线条数，第二个参数是我们当前统计到的交点总数，因此需要将原本的交点总数也加上
                */
            }
        }
}
int main(){
    cin>>n;
    s(n,0);
    cout<<ans;
}

车的攻击

题目描述

$N \times N$ 的国际象棋棋盘上有$K$ 个车，第$i$个车位于第$R_i$行，第$C_i$ 列。求至少被一个车攻击的格子数量。

车可以攻击所有同一行或者同一列的地方。

输入格式

第1 行，2 个整数$N,K$。

接下来K 行，每行2 个整数$R_i,C_i$。

输出格式

1 个整数，表示被攻击的格子数量。

样例 #1

样例输入 #1

1
2
3

3 2
1 2
2 2

样例输出 #1

提示

• 对于30% 的数据，$1 \le N \le 10^3; 1 \le K \le 10^3$；

• 对于60% 的数据，$1 \le N \le 10^6; 1 \le K \le 10^6$；

• 对于100% 的数据，$1 \le N \le 10^9; 1 \le K \le 10^6; 1 \le R_i , C_i \le N$。

#include <iostream>
#include <iomanip>
#include <algorithm>
#include <cstdio>
#include <vector>
#include <queue>
#define ll long long
const int maxn=1e6+5;
using namespace std;
ll n,k;
ll x[maxn],y[maxn];
int main(){

 cin>>n>>k;
        for(ll i=0;i<k;i++){
            
        cin>>x[i]>>y[i];
        }
        sort(x,x+k);
        sort(y,y+k);
        ll sizex=unique(x,x+k)-x;
        ll sizey=unique(y,y+k)-y;
    
        cout<<n*n-(n-sizex)*(n-sizey);
 
}

安全系统

题目描述

特斯拉公司的六位密码被轻松破解后，引发了人们对电动车的安全性能的怀疑。李华听闻后，自己设计了一套密码：

假设安全系统中有 $n$ 个储存区，每个储存区最多能存储存 $2$ 个种类不同的信号（可以不储存任何信号）。有 $0$ 和 $1$ 这两种信号，其中 $0$ 有 $a$ 个，$1$ 有 $b$ 个，单独一个 $0$ 或 $1$ 算一个信号。现要将这些信号储存在储存区中，$0$ 和 $1$ 可以不用全部储存，一个存储区可以存放任意多个 $0$ 和任意多个 $1$。一种不同的储存方案经过李华处理后就将是一串不同的密码。

现在给出 $n,a,b$，求可能的不同储存方案的个数。

输入格式

第一行：共 $3$ 个整数，$n,a,b$。

输出格式

第一行：一个整数，表示方案个数。

样例 #1

样例输入 #1

2 1 1

样例输出 #1

提示

所有 $9$ 种方案如下：

储存区 $1$	储存区 $2$
$\verb!NULL!$	$\verb!NULL!$
$0$	$\verb!NULL!$
$1$	$\verb!NULL!$
$\verb!NULL!$	$0$
$\verb!NULL!$	$1$
$0,1$	$\verb!NULL!$
$\verb!NULL!$	$0,1$
$1$	$0$
$0$	$1$

对于全部数据，$a,b\le 50$，$n+a\le 50$，$n+b\le 50$。

$\text{upd 2022.10.22}$：新增加一组 Hack 数据。

#include<bits/stdc++.h>
using namespace std;
//需要用__int128
inline void read(__int128 &x) {
    x=0;
    int f=1;//判断正负 
    char ch=getchar();//读入字符
    while(ch<'0'||ch>'9') {
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9') {//是数字就读
        x=x*10+ch-'0';//之前结果乘10，加现在读入的
        ch=getchar();
    }
    x*=f;//添上符号返回
}
inline void write(__int128 x) {
    if(x<0) {
        putchar('-');//输出符号
        x=-x;
    }
    if(x>9)write(x/10);//递归输出
    putchar(x%10+'0');//输出个位
}

__int128 bino(__int128 n, __int128 r) 
{
    __int128 ans = 1;
    for (int i = 1; i <= r; ++i) {
        ans *= n - i + 1;
        ans /= i;
    }
    return ans;
}

int main() {
    __int128 n, a, b;
read(n);
    read(a);
    read(b);
    write( bino(a+n, n)*bino(b+n, n));
    return 0;
}

编码

题目描述

编码工作常被运用于密文或压缩传输。这里我们用一种最简单的编码方式进行编码：把一些有规律的单词编成数字。

字母表中共有 $26$ 个字母 $\mathtt{a,b,c,\cdots,z}$，这些特殊的单词长度不超过 $6$ 且字母按升序排列。把所有这样的单词放在一起，按字典顺序排列，一个单词的编码就对应着它在字典中的位置。

例如：

$\verb!a! \to 1$；
$\verb!b! \to 2$；
$\verb!z! \to 26$；
$\verb!ab! \to 27$；
$\verb!ac! \to 28$。

你的任务就是对于所给的单词，求出它的编码。

输入格式

仅一行，被编码的单词。

输出格式

仅一行，对应的编码。如果单词不在字母表中，输出 $0$。

样例 #1

样例输入 #1

ab

样例输出 #1

#include<bits/stdc++.h>
using namespace std;
string s;
int ans,n;
int c(int m,int n)
{
	if(m==0)return 1;
	int mut=1;
	for(int i=n;i>n-m;i--)mut*=i;
	for(int i=m;i>1;i--)mut/=i;
	return mut;
}
//组合数计算
int main()
{
	cin>>s;
    n=s.size();
	for(int i=1;i<n;i++)
		if(s[i]<=s[i-1])
        {
            cout<<0;
            return 0;
        }
	for(int i=1;i<n;i++)
    {
        ans+=c(i,26);
    }
	for(int i=0;i<n;i++)
		for(char j=(i==0?'a':s[i-1]+1);j<s[i];j++)
        {
            ans+=c(n-i-1,'z'-j);
        }
    ans++;
	cout<<ans;

}

[USACO08DEC] Patting Heads S

题面翻译

今天是贝茜的生日，为了庆祝自己的生日，贝茜邀你来玩一个游戏。

贝茜让 $N$ ($1\leq N\leq 10^5$) 头奶牛坐成一个圈。除了 $1$ 号与 $N$ 号奶牛外，$i$ 号奶牛与 $i-1$ 号和 $i+1$ 号奶牛相邻。$N$ 号奶牛与 $1$ 号奶牛相邻。农夫约翰用很多纸条装满了一个桶，每一张包含了一个不一定是独一无二的 $1$ 到 $10^6$ 的数字。

接着每一头奶牛 $i$ 从桶中取出一张纸条 $A_i$。每头奶牛轮流走上一圈，同时拍打所有手上数字能整除在自己纸条上的数字的牛的头，然后做回到原来的位置。牛们希望你帮助他们确定，每一头奶牛需要拍打的牛的数量。

题目描述

It's Bessie's birthday and time for party games! Bessie has instructed the N (1 <= N <= 100,000) cows conveniently numbered 1..N to sit in a circle (so that cow i [except at the ends] sits next to cows i-1 and i+1; cow N sits next to cow 1). Meanwhile, Farmer John fills a barrel with one billion slips of paper, each containing some integer in the range 1..1,000,000.

Each cow i then draws a number A_i (1 <= A_i <= 1,000,000) (which is not necessarily unique, of course) from the giant barrel. Taking turns, each cow i then takes a walk around the circle and pats the heads of all other cows j such that her number A_i is exactly

divisible by cow j's number A_j; she then sits again back in her original position.

The cows would like you to help them determine, for each cow, the number of other cows she should pat.

输入格式

* Line 1: A single integer: N

* Lines 2..N+1: Line i+1 contains a single integer: A_i

输出格式

* Lines 1..N: On line i, print a single integer that is the number of other cows patted by cow i.

样例 #1

样例输入 #1

样例输出 #1

提示

The 5 cows are given the numbers 2, 1, 2, 3, and 4, respectively.

The first cow pats the second and third cows; the second cows pats no cows; etc.

#include<bits/stdc++.h>
using namespace std;
int n;
const int N=1e6+5;
int bac[N],a[N];
int main()
{
	cin>>n;
	for (int i=1;i<=n;i++) cin>>a[i],bac[a[i]]++;
	for (int i=1;i<=n;i++)
    {
		int ans=0;
		bac[a[i]]--;//防止算自己
		for (int fac=1;fac<=sqrt(a[i]);fac++) 
        {  
            if (a[i]%fac==0)
            {
			ans+=bac[fac]+bac[a[i]/fac];
			if (fac==a[i]/fac) ans-=bac[fac];
            }
        }
	//判断因数只需到这即可
		bac[a[i]]++;
		cout<<ans<<'\n';
	}
}

【模板】线性筛素数

题目背景

本题已更新，从判断素数改为了查询第 $k$ 小的素数
提示：如果你使用 cin 来读入，建议使用 std::ios::sync_with_stdio(0) 来加速。

题目描述

如题，给定一个范围 $n$，有 $q$ 个询问，每次输出第 $k$ 小的素数。

输入格式

第一行包含两个正整数 $n,q$，分别表示查询的范围和查询的个数。

接下来 $q$ 行每行一个正整数 $k$，表示查询第 $k$ 小的素数。

输出格式

输出 $q$ 行，每行一个正整数表示答案。

样例 #1

样例输入 #1

样例输出 #1

提示

【数据范围】
对于 $100\%$ 的数据，$n = 10^8$，$1 \le q \le 10^6$，保证查询的素数不大于 $n$。

Data by NaCly_Fish.

//by dpcc
#include<bits/stdc++.h>
using ll=long long;
using namespace std;
#define r0 return 0;
#define  re register
#define rep(i,a,n) for(re int i=a;i<=n;i++)
#define frep(i,a,n) for(re int i=a;i>=n;i--)
int n,x;
const int N=1e8+10;
bool pd[N];
int ans[N];
int n2;
int main(){
	pd[1]=1;
cin>>x>>n;
for(int i=2;i<=x;i++)
{
	if(!pd[i]) ans[++n2]=i;//记录下来
	for(int j=1;j<=n2&&i*ans[j]<=x;j++)
	{
		//此时的素数的个数
		pd[ans[j]*i]=1;
		if(i%ans[j]==0)//退出避免多筛选
		break;
	}
}
rep(i,1,n)
{
	int h;
	cin>>h;
cout<<ans[h]<<'\n';
	

}
	r0
}

素数密度

题目描述

给定区间 $[L,R]$（$1\leq L\leq R < 2^{31}$，$R-L\leq 10^6$），请计算区间中素数的个数。

输入格式

第一行，两个正整数 $L$ 和 $R$。

输出格式

一行，一个整数，表示区间中素数的个数。

样例 #1

样例输入 #1

2 11

样例输出 #1

#include <bits/stdc++.h>
using namespace std;
#define re register
#define ll long long
const int maxn=1e6+1;
ll l,r;
int prime[maxn],cnt,ans;
bool vis[maxn];
inline void Gprime()//线性筛素数,预处理根号R内的素数,这里不赘述了,dalao们肯定都会qwq
{
    for(re int i=2;i<=50000;++i)
    {
        if(!vis[i])prime[++cnt]=i;
        for(re int j=1;i*prime[j]<=50000;j++)
        {
            vis[i*prime[j]]=1;//标记合数
            if(i%prime[j]==0) break;
        }
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>l>>r;
    l=l==1?2:l;//特判L=1的情况
    Gprime();//筛出根号R内的所有质数以及剩下的合数
    memset(vis,0,sizeof(vis));//懒得多开一个数组,沿用函数中的数组时记得清空
    for(re int i=1;i<=cnt;++i)//枚举已经筛出来的质数
    {
        ll p=prime[i],start=(l+p-1)/p*p>2*p?(l+p-1)/p*p:2*p;//我们从大于L的最小的能被p整除的数开始,(l+p-1)就等于ceil(l+p-1),因为有可能会在接下来筛的过程中把自己也一起筛掉,所以在此特判一下
        for(re ll int j=start;j<=r;j+=p)vis[j-l+1]=1;
    }
    for(re int i=1;i<=r-l+1;++i)if(!vis[i])ans++;//r-l+1即为区间长度,遍历区间找没有被标记的元素并累加答案
    cout<<ans;
}

[NOIP2001 普及组] 最大公约数和最小公倍数问题

题目描述

输入两个正整数 $x_0, y_0$，求出满足下列条件的 $P, Q$ 的个数：

$P,Q$ 是正整数。
要求 $P, Q$ 以 $x_0$ 为最大公约数，以 $y_0$ 为最小公倍数。

试求：满足条件的所有可能的 $P, Q$ 的个数。

输入格式

一行两个正整数 $x_0, y_0$。

输出格式

一行一个数，表示求出满足条件的 $P, Q$ 的个数。

样例 #1

样例输入 #1

3 60

样例输出 #1

提示

$P,Q$ 有 $4$ 种：

$3, 60$。
$15, 12$。
$12, 15$。
$60, 3$。

对于 $100\%$ 的数据，$2 \le x_0, y_0 \le {10}^5$。

【题目来源】

NOIP 2001 普及组第二题

#include<bits/stdc++.h>
using namespace std;
long long m,n,ans;
int main(){
	cin>>m>>n;
	if(m==n) ans--;
	n*=m;
	for(long long i=1;i<=sqrt(n);i++){
		if(n%i==0&&__gcd(i,n/i)==m) ans+=2;
	}
	cout<<ans;

}

[NOIP2009 提高组] Hankson 的趣味题

题目描述

Hanks 博士是 BT（Bio-Tech，生物技术) 领域的知名专家，他的儿子名叫 Hankson。现在，刚刚放学回家的 Hankson 正在思考一个有趣的问题。

今天在课堂上，老师讲解了如何求两个正整数 $c_1$ 和 $c_2$ 的最大公约数和最小公倍数。现在 Hankson 认为自己已经熟练地掌握了这些知识，他开始思考一个“求公约数”和“求公倍数”之类问题的“逆问题”，这个问题是这样的：已知正整数 $a_0,a_1,b_0,b_1$，设某未知正整数 $x$ 满足：

$x$ 和 $a_0$ 的最大公约数是 $a_1$；
$x$ 和 $b_0$ 的最小公倍数是 $b_1$。

Hankson 的“逆问题”就是求出满足条件的正整数 $x$。但稍加思索之后，他发现这样的 $x$ 并不唯一，甚至可能不存在。因此他转而开始考虑如何求解满足条件的 $x$ 的个数。请你帮助他编程求解这个问题。

输入格式

第一行为一个正整数 $n$，表示有 $n$ 组输入数据。接下来的$ n$ 行每行一组输入数据，为四个正整数 $a_0,a_1,b_0,b_1$，每两个整数之间用一个空格隔开。输入数据保证 $a_0$ 能被 $a_1$ 整除，$b_1$ 能被 $b_0$ 整除。

输出格式

共 $n$ 行。每组输入数据的输出结果占一行，为一个整数。

对于每组数据：若不存在这样的 $x$，请输出 $0$，若存在这样的 $x$，请输出满足条件的 $x$ 的个数；

样例 #1

样例输入 #1

1
2
3

2 
41 1 96 288 
95 1 37 1776

样例输出 #1

1
2

6 
2

提示

【样例解释】

第一组输入数据，$x$ 可以是 $9,18,36,72,144,288$，共有 $6$ 个。

第二组输入数据，$x$ 可以是 $48,1776$，共有 $2$ 个。

【数据范围】

对于 $50\%$ 的数据，保证有 $1\leq a_0,a_1,b_0,b_1 \leq 10000$ 且 $n \leq 100$。
对于 $100\%$ 的数据，保证有 $1 \leq a_0,a_1,b_0,b_1 \leq 2 \times 10^9$ 且 $n≤2000$。

NOIP 2009 提高组第二题

#include<cstdio>
using namespace std;
int gcd(int a,int b) {
    return b==0?a:gcd(b,a%b);
}
int main() {
    int T;
    cin>>T;
    while(T--) {
        int a0,a1,b0,b1;
        cin>>a0>>a1>>b0>>b1;
        int p=a0/a1,q=b1/b0,ans=0;
        for(int x=1;x*x<=b1;x++) 
            if(b1%x==0){
                if(x%a1==0&&gcd(x/a1,p)==1&&gcd(q,b1/x)==1) ans++;
                int y=b1/x;//得到另一个因子
                if(x==y) continue; 
                if(y%a1==0&&gcd(y/a1,p)==1&&gcd(q,b1/y)==1) ans++;
            }
     cout<<ans<<'\n';
    }
}
//两个最大公约数和最小公倍数的结论

[NOIP2009 普及组] 细胞分裂

题目描述

Hanks 博士是 BT（Bio-Tech，生物技术）领域的知名专家。现在，他正在为一个细胞实验做准备工作：培养细胞样本。

Hanks 博士手里现在有 $N$ 种细胞，编号从 $1 \sim N$，一个第 $i$ 种细胞经过 $1$ 秒钟可以分裂为 $S_i$ 个同种细胞（$S_i$ 为正整数）。现在他需要选取某种细胞的一个放进培养皿，让其自由分裂，进行培养。一段时间以后，再把培养皿中的所有细胞平均分入 $M$ 个试管，形成 $M$ 份样本，用于实验。Hanks 博士的试管数 $M$ 很大，普通的计算机的基本数据类型无法存储这样大的 $M$ 值，但万幸的是，$M$ 总可以表示为 $m_1$ 的 $m_2$ 次方，即 $M = m_1^{m_2}$，其中 $m_1,m_2$ 均为基本数据类型可以存储的正整数。

注意，整个实验过程中不允许分割单个细胞，比如某个时刻若培养皿中有 $4$ 个细胞，Hanks 博士可以把它们分入 $2$ 个试管，每试管内 $2$ 个，然后开始实验。但如果培养皿中有 $5$ 个细胞，博士就无法将它们均分入 $2$ 个试管。此时，博士就只能等待一段时间，让细胞们继续分裂，使得其个数可以均分，或是干脆改换另一种细胞培养。

为了能让实验尽早开始，Hanks 博士在选定一种细胞开始培养后，总是在得到的细胞“刚好可以平均分入 $M$ 个试管”时停止细胞培养并开始实验。现在博士希望知道，选择哪种细胞培养，可以使得实验的开始时间最早。

输入格式

第一行，有一个正整数 $N$，代表细胞种数。

第二行，有两个正整数 $m_1,m_2$，以一个空格隔开，即表示试管的总数 $M = m_1^{m_2}$。

第三行有 $N$ 个正整数，第 $i$ 个数 $S_i$ 表示第 $i$ 种细胞经过 $1$ 秒钟可以分裂成同种细胞的个数。

输出格式

一个整数，表示从开始培养细胞到实验能够开始所经过的最少时间（单位为秒）。

如果无论 Hanks 博士选择哪种细胞都不能满足要求，则输出整数 $-1$。

样例 #1

样例输入 #1

1
2
3

1 
2 1 
3

样例输出 #1

-1

样例 #2

样例输入 #2

1
2
3

2
24 1
30 12

样例输出 #2

提示

【输入输出样例 #1 说明】

经过 $1$ 秒钟，细胞分裂成 $3$ 个，经过 $2$ 秒钟，细胞分裂成 $9$个，……，可以看出无论怎么分裂，细胞的个数都是奇数，因此永远不能分入 $2$ 个试管。

【输入输出样例 #2 说明】

第 $1$ 种细胞最早在 $3$ 秒后才能均分入 $24$ 个试管，而第 $2$ 种最早在 $2$ 秒后就可以均分（每试管 $144 / {24}^1 = 6$ 个）。故实验最早可以在 $2$ 秒后开始。

【数据范围】

对于 $50 \%$ 的数据，有 $m_1^{m_2} \le 30000$。

对于所有的数据，有 $1 \le N \le 10000$，$1 \le m_1 \le 30000$，$1 \le m_2 \le 10000$，$1 \le S_i \le 2 \times {10}^9$。

NOIP 2009 普及组第三题

#include<bits/stdc++.h>
const int  t= 2147483647;
    using namespace std;
    struct node{
        int number,count;
    }a[101];
    int m1,m2,n,top;
    int main()
    {
     cin>>n>>m1>>m2;
        int x=m1;
        for(int i=2;i<=x;i++)
        {
            if(x%i==0)
            {
                a[++top].number=i;
                while(x%i==0)//分解质因数
                {
                    x/=i;
                    a[top].count++;//找出m1；
                }
                a[top].count*=m2;//试管总数
            }
        }
        //分解并求出总数的个数
        int minn=t;
        for(int i=1;i<=n;i++)
        {
            int m;
            cin>>m;
            bool b=true;
            for(int j=1;j<=top;j++)
            	b=b&&(m%a[j].number==0);
            //能不能分解
            if(b)
            {
                int maxx=0;
                for(int j=1;j<=top;j++)
                {
                    int ans=0,mx=m;
                    while(mx%a[j].number==0)//分解质因数
                    {
                        mx/=a[j].number;
                        ans++;
                    }
                    ans=(a[j].count-1)/ans+1;
                    maxx=max(maxx,ans);
                }
                //可以的话就进行分解
                minn=min(minn,maxx);//最少秒时可以装进试管
            }
        }
        if(minn==t)
        	cout<<-1;//如果没有改变，输出-1
        else 
        	cout<<minn;//输出结果
    }

计算分数

题目描述

Csh 被老妈关在家里做分数计算题，但显然他不愿意做这么多复杂的计算。况且在家门口还有 Xxq 在等着他去一起看电影。为了尽快地能去陪 Xxq 看电影，他把剩下的计算题交给了你，你能帮他解决问题吗？

输入格式

输入一行，为一个分数计算式。

计算式中只包含数字、+、-、/。其中 / 为分数线，分数线左边为分子，右边为分母。输入数据保证不会出现繁分数。如果输入计算式的第一项为正，不会有前缀 + 号；若为负，会有前缀 - 号。

所有整数均以分数形式出现。

输出格式

输出一行，为最后的计算结果（用为整数则用整数表示，否则用最简分数表示）。

保证答案内出现的所有数（如果答案是分数即为分子和分母）均在 $32$ 位带符号整数的表示范围之内。

样例 #1

样例输入 #1

1	2/1+1/3-1/4

样例输出 #1

25/12

提示

数据范围及约定

对于所有测试点，输入计算式长度在 $100$ 以内，分子、分母在 $1000$ 以内。同时保证，直接从前往后直接计算分数的和或者差，然后立刻化简，这么做的中间结果不会超过 int 的范围。

注意输入的分数不一定是最简分数。

2024/2/13 添加 2 组 hack 数据。

//by dpcc
#include<bits/stdc++.h>
using ll=long long;
using namespace std;
#define r0 return 0;
#define  re register
#define rep(i,a,n) for(re int i=a;i<=n;i++)
#define frep(i,a,n) for(re int i=a;i>=n;i--)
int n;
inline int gcd(int a,int b)
{
	return b?gcd(b,a%b):a;
}
int main(){
int a,b,fz,fm,c;
	char p,t;
	cin>>fz>>t>>fm;
	while(cin>>p)
	{
		cin>>a>>t>>b;
		if(p=='+') fz=fz*b+fm*a;
		else fz=fz*b-fm*a;	
		fm*=b,c=gcd(fz,fm),fz/=c,fm/=c;
	}
	if(fm==1) cout<<fz;
	else if(fm<0) cout<<-fz<<'/'<<-fm;
	else cout<<fz<<'/'<<fm;
	r0
}

[Code+#1] 晨跑

题目描述

“无体育，不清华”、“每天锻炼一小时，健康工作五十年，幸福生活一辈子”

在清华，体育运动绝对是同学们生活中不可或缺的一部分。为了响应学校的号召，模范好学生王队长决定坚持晨跑。不过由于种种原因，每天都早起去跑步不太现实，所以王队长决定每$a$天晨跑一次。换句话说，假如王队长某天早起去跑了步，之后他会休息$a-1$天，然后第$a$天继续去晨跑，并以此类推。

王队长的好朋友小钦和小针深受王队长坚持锻炼的鼓舞，并决定自己也要坚持晨跑。为了适宜自己的情况，小钦决定每$b$天早起跑步一次，而小针决定每$c$天早起跑步一次。

某天早晨，王队长、小钦和小针在早起跑步时相遇了，他们非常激动、相互鼓励，共同完成了一次完美的晨跑。为了表述方便，我们把三位同学相遇的这天记为第$0$天。假设三位同学每次晨跑的时间段和路线都相同，他们想知道，下一次三人在跑步时相遇是第几天。由于三位同学都不会算，所以希望由聪明的你来告诉他们答案。

输入格式

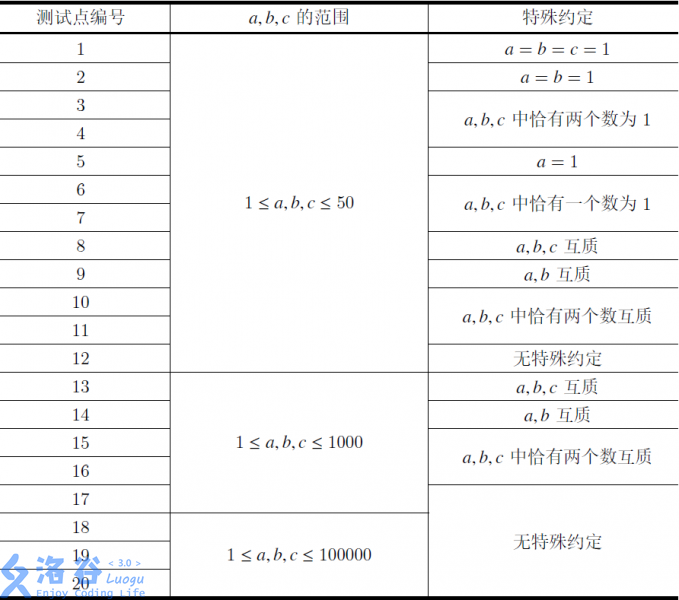
输入共一行，包含三个正整数$a,b,c$，表示王队长每隔$a$天晨跑一次、小钦每隔$b$天晨跑一次且小针每隔$c$天晨跑一次。

输出格式

输出共一行，包含一个正整数$x$，表示三位同学下次将在第$x$天相遇。

样例 #1

样例输入 #1

2 3 5

样例输出 #1

样例 #2

样例输入 #2

3 4 6

样例输出 #2

样例 #3

样例输入 #3

1	10 100 1000

样例输出 #3

提示

来自 CodePlus 2017 11 月赛，清华大学计算机科学与技术系学生算法与竞赛协会荣誉出品。

Credit：idea/何昊天命题/何昊天验题/卢政荣

Git Repo：https://git.thusaac.org/publish/CodePlus201711

感谢腾讯公司对此次比赛的支持。

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
long long a,b,c;
long long gcd(long long x,long long y){
	if (x%y==0){
		return y;
	}
	return gcd(y,x%y);//重点
}

long long lcm(long long x,long long y){//最小公倍数（用GCD求）
	return x*y/gcd(x,y);
} 

int main()
{

	cin>>a>>b>>c;//读入
	long long ans=0;
	ans=lcm(a,lcm(b,c));//直接求答案
	cout<<ans;
}

又是毕业季II

题目背景

“叮铃铃铃”，随着高考最后一科结考铃声的敲响，三年青春时光顿时凝固于此刻。毕业的欣喜怎敌那离别的不舍，憧憬着未来仍毋忘逝去的歌。一千多个日夜的欢笑和泪水，全凝聚在毕业晚会上，相信，这一定是一生最难忘的时刻！

题目描述

彩排了一次，老师不太满意。当然啦，取每位同学的号数来找最大公约数显然不太合理。于是老师给每位同学评了一个能力值。于是现在问题变为，从 $n$ 个学生中挑出 $k$ 个人使得他们的默契程度（即能力值的最大公约数）最大。但因为节目太多了，而且每个节目需要的人数又不知道。老师想要知道所有情况下能达到的最大默契程度是多少。这下子更麻烦了，还是交给你吧~

PS：一个数的最大公约数即本身。

输入格式

第一行一个正整数 $n$。

第二行为 $n$ 个空格隔开的正整数，表示每个学生的能力值。

输出格式

总共 $n$ 行，第 $i$ 行为 $k=i$ 情况下的最大默契程度。

样例 #1

样例输入 #1

1
2

4
1 2 3 4

样例输出 #1

提示

【题目来源】

lzn 原创

【数据范围】

记输入数据中能力值的最大值为 $\textit{inf}$。

对于 $20\%$ 的数据，$n \leq 5$，$\textit{inf}\leq 10^3$；
对于另 $30\%$ 的数据，$n \leq 100$，$\textit{inf} \leq 10$；

对于 $100\%$ 的数据，$n \leq 10^4$，$\textit{inf} \leq 10^6$。

//by dpcc
#include<bits/stdc++.h>
using ll=long long;
using namespace std;
#define r0 return 0;
#define  re register
#define rep(i,a,n) for(re int i=a;i<=n;i++)
#define frep(i,a,n) for(re int i=a;i>=n;i--)
int n;
const int N=1e6+10;
int c[N];
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
cin>>n;
int x;
int t=0;
rep(i,1,n)
{
	cin>>x;
	t=max(t,x);
	rep(j,1,sqrt(x))
	{
		if(x%j==0)
		{
			c[j]++;
		if(j*j!=x)
		{
			c[x/j]++;
		}	
		}
	}	
}
rep(i,1,n)
{
	while(c[t]<i)
	{
		t--;
	}
	cout<<t<<'\n';	
}
	r0
}
 1、 求出每个因数出现的次数。

* 2、 对于每个次数记录最大的因数。

* 3、 根据f[k]=max(f[k],f[k+1])逆向递推。

# 添加括号III

题目描述

现在给出一个表达式，形如 $a_{1}/a_{2}/a_{3}/.../a_{n}$。

如果直接计算，就是一个个除过去，比如 $1/2/1/4 = 1/8$。

然而小$\text{A}$看到一个分数感觉很不舒服，希望通过添加一些括号使其变成一个整数。一种可行的办法是 $(1/2)/(1/4)=2$ 。

现在给出这个表达式，求问是否可以通过添加一些括号改变运算顺序使其成为一个整数。

输入格式

一个测试点中会有多个表达式。

第一行 $t$ ，表示表达式数量。

对于每个表达式，第一行是 $n$，第二行 $n$ 个数，第 $i$ 个数表示 $a_{i}$。

输出格式

输出 $t$ 行。

对于每个表达式，如果可以通过添加括号改变顺序使其变成整数，那么输出 Yes，否则输出 No。

样例 #1

样例输入 #1

样例输出 #1

1
2

Yes
No

提示

对于 $40\%$ 的数据，$n \le 16$。
对于 $70\%$ 的数据，$n \le 100$。
对于 $100\%$ 的数据， $2 \le n \le 10000$，$1 \le t \le 100$，$1 \le a_{i}\le 2^{31}-1$。

#include<bits/stdc++.h>
using namespace std;
long long T,i,n,j,a[100010];
int main(){	
	cin>>T;
	for(i=1;i<=T;i++){
cin>>n;
		for(j=1;j<=n;j++)
			cin>>a[j];
		for(j=1;j<=n;j++){
			if(j==2)//特判此时下标是二的时候
			continue;
			a[2]=a[2]/__gcd(a[2],a[j]);//依次除以这几个数的最大公约数
			if(a[2]==1){
				cout<<"YES"<<'\n';
				break;
			}
		}
		if(j>n)
		cout<<"NO"<<"\n";
	} 
  
}
//有点贪心罢（就让一个数字做分母就好了

zzc 种田

题目背景

可能以后 zzc 就去种田了。

题目描述

田地是一个巨大的矩形，然而 zzc 每次只能种一个正方形,而每种一个正方形时 zzc 所花的体力值是正方形的周长，种过的田不可以再种，zzc 很懒还要节约体力去泡妹子，想花最少的体力值去种完这块田地，问最小体力值。

输入格式

两个正整数 $x,y$，表示田地的长和宽。

输出格式

输出最小体力值。

样例 #1

样例输入 #1

1 10

样例输出 #1

样例 #2

样例输入 #2

2 2

样例输出 #2

提示

$1\le x,y\le 10^{16}$。

#include<bits/stdc++.h>
using namespace std;
int main(){
    long long x,y,ans=0;
    cin>>x>>y;
    while(x&&y){                      
                swap(x,y);                     
                ans+=4*y*(x/y);         
                x%=y;  
    }
    cout<<ans;

}

签到题

题目背景

这是一道签到题！

建议做题之前仔细阅读数据范围！

题目描述

我们定义一个函数：$\operatorname{qiandao}(x)$ 为小于等于 $x$ 的数中，与 $x$ 不互质的数的个数。

这题作为签到题，给出 $l$ 和 $r$，求出：

\[\sum_{i=l}^r \operatorname{qiandao}(i)\bmod 666623333\]

输入格式

一行两个整数，$l$、$r$。

输出格式

一行一个整数表示答案。

样例 #1

样例输入 #1

233 2333

样例输出 #1

样例 #2

样例输入 #2

1	2333333333 2333666666

样例输出 #2

153096296

提示

对于 $30\%$ 的数据，$l,r\leq 10^3$。
对于 $60\%$ 的数据，$l,r\leq 10^7$。
对于 $100\%$ 的数据，$1 \leq l \leq r \leq 10^{12}$，$r-l \leq 10^6$。

一点也不签到的说（）

盯着半天了

前置知识：欧拉函数（）+欧拉筛（可恶的）

需要注意的是，欧拉函数是个值，不是一个集合。

#include<bits/stdc++.h>
#define MAXN 1000005
#define MOD 666623333
using namespace std;
long long l,r,ans,BASE;
int cnt;
bool isprime[MAXN];
long long prime[MAXN],A[MAXN],B[MAXN];
void shai()
{
    for(int i=2;i<=MAXN;i++)
    {
        if(!isprime[i]) prime[++cnt]=i;
        for(int j=2*i;j<=MAXN;j+=i)
            isprime[j]=1;
    }
}
//欧拉筛直接筛出素数
void work()
{
	int i=1;
    while(prime[i]*prime[i]<=r)
    {
    	long long p=prime[i];
    	for(int x=(p-l%p)%p;x<=r-l;x+=p)
    	{
    		A[x]/=p,A[x]*=p-1;
    		while(B[x]%p==0)
				B[x]/=p;
		}
        i++;
	}
}
//求欧拉函数
int main()
{
    shai();
  cin>>l>>r;
    BASE=l;
    for(long long i=l;i<=r;i++)
    	A[i-BASE]=i,B[i-BASE]=i;
    work();
    for(int i=0;i<=r-l;i++) 
	{
    	if(B[i]!=1) A[i]/=B[i],A[i]*=(B[i]-1);
		ans=(ans+i+BASE-A[i])%MOD;
	}
	cout<<ans;
}

欧拉筛和欧拉函数会专门开专题的，现在一知半解

[AHOI2005] 约数研究

题目描述

科学家们在 Samuel 星球上的探险得到了丰富的能源储备，这使得空间站中大型计算机 Samuel II 的长时间运算成为了可能。由于在去年一年的辛苦工作取得了不错的成绩，小联被允许用 Samuel II 进行数学研究。

小联最近在研究和约数有关的问题，他统计每个正数 $N$ 的约数的个数，并以 $f(N)$ 来表示。例如 $12$ 的约数有 $1,2,3,4,6,12$，因此 $f(12)=6$。下表给出了一些 $f(N)$ 的取值：

$N$	$1$	$2$	$3$	$4$	$5$	$6$
$f(N)$	$1$	$2$	$2$	$3$	$2$	$4$

现在请你求出：

\[ \sum_{i=1}^n f(i) \]

输入格式

输入一个整数 $n$。

输出格式

输出答案。

样例 #1

样例输入 #1

样例输出 #1

提示

对于 $20\%$ 的数据，$N \leq 5000$；
对于 $100\%$ 的数据，$1 \leq N \leq 10^6$。

#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int n;
	cin >> n;
	int ans = 0;
	for (int i = 1; i <= n; i++)
	{
		for (int j = i; j <= n; j+=i)
		{
			ans++;
		}
	}
	cout << ans;
}

因子和

题目描述

输入两个整数 $a$ 和 $b$，求 $a^b$ 的因子和。

由于结果太大，只要输出它对 $9901$ 取模的结果。

输入格式

仅一行，为两个整数 $a$ 和 $b$。

输出格式

输出一行一个整数表示答案对 $9901$ 取模的结果。

样例 #1

样例输入 #1

2 3

样例输出 #1

提示

数据规模与约定

对于全部的测试点，保证 $1 \leq a \leq 5 \times 10^7$，$0 \leq b \leq 5 \times 10^7$。

再分解，可以分解出因数

#include<bits/stdc++.h>
using ll=long long;
using namespace std;
ll a,b,ans=1,mod=9901;
ll ksm(ll x,ll y)
{
	ll res=1;
	while(y){
		if(y%2==1)res=res*x%mod;
		x=x*x%mod;
		y>>=1;
	}
	return res;
}
//快速幂求和
ll sum(ll x,ll y)
{
	if(x==0)return 1;
	if(x%2)return sum(x/2,y)*(1+ksm(y,x/2+1))%mod;
    //偶数项
	return (sum(x/2-1,y)*(1+ksm(y,x/2+1))+ksm(y,x/2))%mod;
    //奇数项
}
   //等比数列和
int main (){
	cin>>a>>b;
	for(int i=2;i<=sqrt(a);i++)
    {
		int c=0;
		while(a%i==0)
        {
			a/=i;
			c++;
		}
        //分解质因数
		ans=ans*sum(c*b,i)%mod;
        //再进行求和
	}
	if(a!=1)
	ans=ans*sum(b,a)%mod;
	cout<<ans;
}

储存区 \(1\)	储存区 \(2\)
\(\verb!NULL!\)	\(\verb!NULL!\)
\(0\)	\(\verb!NULL!\)
\(1\)	\(\verb!NULL!\)
\(\verb!NULL!\)	\(0\)
\(\verb!NULL!\)	\(1\)
\(0,1\)	\(\verb!NULL!\)
\(\verb!NULL!\)	\(0,1\)
\(1\)	\(0\)
\(0\)	\(1\)