字符串

【模板】KMP

题目描述

给出两个字符串 \(s_1\) 和 \(s_2\)，若 \(s_1\) 的区间 \([l, r]\) 子串与 \(s_2\) 完全相同，则称 \(s_2\) 在 \(s_1\) 中出现了，其出现位置为 \(l\)。
现在请你求出 \(s_2\) 在 \(s_1\) 中所有出现的位置。

定义一个字符串 \(s\) 的 border 为 \(s\) 的一个非 \(s\) 本身的子串 \(t\)，满足 \(t\) 既是 \(s\) 的前缀，又是 \(s\) 的后缀。
对于 \(s_2\)，你还需要求出对于其每个前缀 \(s'\) 的最长 border \(t'\) 的长度。

输入格式

第一行为一个字符串，即为 \(s_1\)。
第二行为一个字符串，即为 \(s_2\)。

输出格式

首先输出若干行，每行一个整数，按从小到大的顺序输出 \(s_2\) 在 \(s_1\) 中出现的位置。
最后一行输出 \(|s_2|\) 个整数，第 \(i\) 个整数表示 \(s_2\) 的长度为 \(i\) 的前缀的最长 border 长度。

样例 #1

样例输入 #1

1
2
ABABABC
ABA

样例输出 #1

1
2
3
1
3
0 0 1

提示

样例 1 解释

。

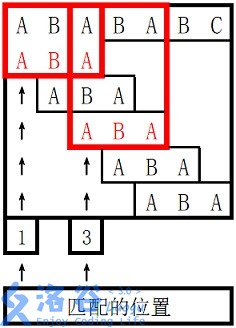
对于 \(s_2\) 长度为 \(3\) 的前缀 ABA，字符串 A 既是其后缀也是其前缀，且是最长的，因此最长 border 长度为 \(1\)。

数据规模与约定

本题采用多测试点捆绑测试，共有 3 个子任务。

  • Subtask 1（30 points）：\(|s_1| \leq 15\)，\(|s_2| \leq 5\)。
  • Subtask 2（40 points）：\(|s_1| \leq 10^4\)，\(|s_2| \leq 10^2\)。
  • Subtask 3（30 points）：无特殊约定。

对于全部的测试点，保证 \(1 \leq |s_1|,|s_2| \leq 10^6\)，\(s_1, s_2\) 中均只含大写英文字母。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include<bits/stdc++.h>
#define N 1000010
using namespace std;
int kmp[N];
int la,lb,j; 
string a;
string b;
int main()
{
    cin>>a;
    cin>>b;
    a=" "+a;
    b=" "+b;
    la=a.length()-1;
    lb=b.length()-1;
    for (int i=2;i<=lb;i++)
	   {     
	   while(j&&b[i]!=b[j+1])
        j=kmp[j];    
       if(b[j+1]==b[i])
           j++;    
        kmp[i]=j;
       }
    j=0;
    for(int i=1;i<=la;i++)
	   {
          while(j>0&&b[j+1]!=a[i])
           j=kmp[j];
          if (b[j+1]==a[i]) 
           j++;
          if (j==lb) 
		  {
		  cout<<i-lb+1<<'\n';
		  j=kmp[j];
		  }
       }

    for (int i=1;i<=lb;i++)
    cout<<kmp[i]<<" ";

}

详见KMP一文

kmp[i] 用于记录当匹配到模式串的第 i 位之后失配,该跳转到模式串的哪个位置

一个人能走的多远不在于他在顺境时能走的多快，而在于他在逆境时多久能找到曾经的自己。 ————KMP

[BOI2009] Radio Transmission 无线传输

题目描述

给你一个字符串 \(s_1\)，它是由某个字符串 \(s_2\) 不断自我连接形成的（保证至少重复 \(2\) 次）。但是字符串 \(s_2\) 是不确定的，现在只想知道它的最短长度是多少。

输入格式

第一行一个整数 \(L\)，表示给出字符串的长度。

第二行给出字符串 \(s_1\) 的一个子串，全由小写字母组成。

输出格式

仅一行，表示 \(s_2\) 的最短长度。

样例 #1

样例输入 #1

1
2
8
cabcabca

样例输出 #1

1
3

提示

样例输入输出 1 解释

对于样例，我们可以利用 \(\texttt{abc}\) 不断自我连接得到 \(\texttt{abcabcabcabc}\)，读入的 \(\texttt{cabcabca}\)，是它的子串。

规模与约定

对于全部的测试点，保证 \(1 < L \le 10^6\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<bits/stdc++.h>
#define N 1000010
using namespace std;
int kmp[N];
int la,j;
string a;
int main()
{
	int n;
	cin>>n;
    cin>>a;
  a=" "+a;
  for(int i=2;i<=n;i++)
  {
  	while(j&&a[i]!=a[j+1])
  	{
  		j=kmp[j];
	  }
	  if(a[j+1]==a[i])
	  {
	  	j++;
	  }
	  kmp[i]=j;
  }
  cout<<n-kmp[n];
}

我们要求解的是ss的循环子串，结论是：

\[ ans=n-next[n] \] 设最小循环子串长度为 x，那么可以得到next[x]==0;

证明：

如果next[x]==len（0<len<x）,那么就有s[len]==s[x];

那么去掉s[x]后得到的[1,x-1]依旧是原串的循环子串，

因为 x 为最短长度，所以可得 next[x]一定为0;

  • 所以我们可以推论得到next[x+1]==1; next[x+2]==2...
  • 最终得到 nxet[n]==n-x

超级帅气的题解，鸣谢Caicz大佬

大佬的签名：

时代浪潮下的我，时代浪潮之上的你们

魔族密码

题目背景

风之子刚走进他的考场，就……

花花：当当当当~~偶是魅力女皇——花花！！^^（华丽出场，礼炮，鲜花）

风之子：我呕……（杀死人的眼神）快说题目！否则……-_-###

题目描述

花花：……咦好冷我们现在要解决的是魔族的密码问题（自我陶醉：搞不好魔族里面还会有人用密码给我和菜虫写情书咧，哦活活，当然是给我的比较多拉*_*）。

魔族现在使用一种新型的密码系统。每一个密码都是一个给定的仅包含小写字母的英文单词表，每个单词至少包含 \(1\) 个字母，至多 \(75\) 个字母。如果在一个由一个词或多个词组成的表中，除了最后一个以外，每个单词都被其后的一个单词所包含，即前一个单词是后一个单词的前缀，则称词表为一个词链。例如下面单词组成了一个词链：

  • \(\verb!i!\)；
  • \(\verb!int!\)；
  • \(\verb!integer!\)。

但下面的单词不组成词链：

  • \(\verb!integer!\)；
  • \(\verb!intern!\)。

现在你要做的就是在一个给定的单词表中取出一些词，组成最长的词链，就是包含单词数最多的词链。将它的单词数统计出来，就得到密码了。

风之子：密码就是最长词链所包括的单词数阿……

输入格式

这些文件的格式是，第一行为单词表中的单词数 \(N\)（\(1 \le N \le 2000\)），下面每一行有一个单词，按字典顺序排列，中间也没有重复的单词。

输出格式

输出共一行，一个整数，表示密码。

样例 #1

样例输入 #1

1
2
3
4
5
6
5
i
int
integer
intern
internet

样例输出 #1

1
4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<bits/stdc++.h>
using namespace std;
char s[2010][80];
int f[2010],n,ans;
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>s[i];
		f[i]=1;
		for(int j=i-1;j>=1;j--)
            //倒序保证长的先接上，小贪心
			if(strstr(s[i],s[j])==s[i])
			/*判断s2是否为s1的子串。
如果没找到，返回NULL;
如果找到了，返回这个子串第一个字符的地址。
*/
				f[i]=max(f[j]+1,f[i]);
        //经典dp了
		ans=max(f[i],ans);
        //记录答案
	}
	cout<<ans;
}

当然，这并不符合本题的字典树属性()

于是是时候写（抄）一篇字典树了（）

以下为模板和详细解释

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
const int N = 1000050;
int trie[N][26];
//N是树的层数
int cnt[N];
//看是不是以这个字母结尾，以及如果以这个字母结尾，究竟是结尾了多少次呢
int id;
//节点的编号
void insert(string s)
    //插入函数
    //需要一个字符串
{
	int p = 0;
    //插入自然也是从根节点开始，注意，根节点不存储字符
	for (int i = 0; i < s.size(); i++)
        //遍历字符串
	{
		int x = s[i] - 'a';
        //进行字母的一个小变形，因为我们得到0-25
		if (trie[p][x] == 0) trie[p][x] = ++id;
        //如果没有所对应的字母没有，就建一个
		p = trie[p][x];
        //然后接下来p就是这个刚建立的字母哩
	}
	cnt[p]++;
    //遍历完了，出循环，也就是说字母存储结束了，但我们需要知道，于是cnt用来记录结束否
}
//插入就讲完了，感觉还是很清晰的
int  find(string s)
{
	int p = 0;
    //查找一样从根节点开始查找
	for (int i = 0; i < s.size(); i++)
	{
        //遍历字符串
		int x = s[i] - 'a';C++
        //依然变形
		if (trie[p][x] == 0)return 0;
        //如果没有，就返回
		p = trie[p][x];
        //有的话就好了，就继续往下搜
	}
	return cnt[p];
    //遍历完了，康康是不是结束的那个节点，妙哉啊
}

本题只需要插入不需要查找，因为只需要在插入那里加个计算即可（）

详见代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <bits/stdc++.h>
using namespace std;
using ll=long long;
const int N = 1000050;
int trie[N][26];
//N是树的层数
int cnt[N];
int ans;
//看是不是以这个字母结尾，以及如果以这个字母结尾，究竟是结尾了多少次呢
int id;
//节点的编号
void insert(string s)
    //插入函数
    //需要一个字符串
{
	int p = 0;
	int _ans=0;
    //插入自然也是从根节点开始，注意，根节点不存储字符
	for (int i = 0; i < s.size(); i++)
        //遍历字符串
	{
		int x = s[i] - 'a';
        //进行字母的一个小变形，因为我们得到0-25
		if (trie[p][x] == 0) trie[p][x] = ++id;
        //如果没有所对应的字母没有，就建一个
		p = trie[p][x];
		_ans+=cnt[p];
        //然后接下来p就是这个刚建立的字母哩
	}
	if(_ans>=ans)
	{
		ans=_ans+1;
	}
	cnt[p]++;
    //遍历完了，出循环，也就是说字母存储结束了，但我们需要知道，于是cnt用来记录结束否
}
//插入就讲完了，感觉还是很清晰的
int main()
{
int n;
cin>>n;
	for(int i=1;i<=n;i++)
     {
       string s;
       cin>>s;
       insert(s);
     }
     cout<<ans;	
}

于是他错误的点名开始了

题目背景

XS中学化学竞赛组教练是一个酷爱炉石的人。

他会一边搓炉石一边点名以至于有一天他连续点到了某个同学两次，然后正好被路过的校长发现了然后就是一顿欧拉欧拉欧拉（详情请见已结束比赛 CON900）。

题目描述

这之后校长任命你为特派探员，每天记录他的点名。校长会提供化学竞赛学生的人数和名单，而你需要告诉校长他有没有点错名。（为什么不直接不让他玩炉石。）

输入格式

第一行一个整数 \(n\)，表示班上人数。

接下来 \(n\) 行，每行一个字符串表示其名字（互不相同，且只含小写字母，长度不超过 \(50\)）。

第 \(n+2\) 行一个整数 \(m\)，表示教练报的名字个数。

接下来 \(m\) 行，每行一个字符串表示教练报的名字（只含小写字母，且长度不超过 \(50\)）。

输出格式

对于每个教练报的名字，输出一行。

如果该名字正确且是第一次出现，输出 OK，如果该名字错误，输出 WRONG，如果该名字正确但不是第一次出现，输出 REPEAT。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
10
5  
a
b
c
ad
acd
3
a
a
e

样例输出 #1

1
2
3
OK
REPEAT
WRONG

提示

  • 对于 \(40\%\) 的数据，\(n\le 1000\)，\(m\le 2000\)。
  • 对于 \(70\%\) 的数据，\(n\le 10^4\)，\(m\le 2\times 10^4\)。
  • 对于 \(100\%\) 的数据，\(n\le 10^4\)，\(m≤10^5\)。

\(\text{upd 2022.7.30}\)：新增加一组 Hack 数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//哈希走过场
#include<bits/stdc++.h>
using namespace std;
map<string,int>a; 
string s;
int n,m;
int main(){
    cin>>n;
    while(n--){
    	cin>>s;
    	a[s]=1;
    }
    cin>>m;
    while(m--){
    	cin>>s;
    	if(a[s]==1){puts("OK");a[s]=2;}
        //如果正确，直接打，设为不正确
    	else if(a[s]==2)puts("REPEAT");
        //如果又出现了，那就输出
    	else puts("WRONG");
        //这时候哈希匹配不上，错误
    }

}

其实字典树也可以做的

就是普通的查找

多一个变量记录被查找过

剩下的好像没有了（）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include<bits/stdc++.h>
using namespace std;

char s[100];
int cnt = 1;

struct node
{
    int ch[26];
    int word;
    
}trie[1000000];

void build(char x[])
{
    int len = strlen(x);
    int now = 1;
    for(int i = 0; i < len; ++i)
    {
        if(!trie[now].ch[x[i]-'a'])
            trie[now].ch[x[i]-'a'] = ++cnt;
        now = trie[now].ch[x[i]-'a'];
    }
    trie[now].word = 1;
}

void check(char x[])
{
    int len = strlen(x);
    int now = 1;
    for(int i = 0; i < len; ++i)
    {
        if(!trie[now].ch[x[i]-'a'])
        {
            puts("WRONG");
            return;
        }
        now = trie[now].ch[x[i]-'a'];
    }
    if(trie[now].word == 1)
    {
        puts("OK");
     trie[now].word++;
        return;
    }
    else if(trie[now].word == 0)
    {
        puts("WRONG");

        return;
    }
    else 
    {
        puts("REPEAT");
        return;
    }
}

int main()
{
    int n, m;
    cin>>n;
    for(int i = 1; i <= n; ++i)
    {
        cin>>s;
        build(s);
    }
    cin>>m;
    for(int i = 1; i <= m; ++i)
    {
        cin>>s;
        check(s);
    }
    return 0;
}

最长异或路径

题目描述

给定一棵 \(n\) 个点的带权树，结点下标从 \(1\) 开始到 \(n\)。寻找树中找两个结点，求最长的异或路径。

异或路径指的是指两个结点之间唯一路径上的所有边权的异或。

输入格式

第一行一个整数 \(n\)，表示点数。

接下来 \(n-1\) 行，给出 \(u,v,w\) ，分别表示树上的 \(u\) 点和 \(v\) 点有连边，边的权值是 \(w\)。

输出格式

一行，一个整数表示答案。

样例 #1

样例输入 #1

1
2
3
4
4
1 2 3
2 3 4
2 4 6

样例输出 #1

1
7

提示

最长异或序列是 \(1,2,3\)，答案是 \(7=3\oplus 4\)。

数据范围

\(1\le n \le 100000;0 < u,v \le n;0 \le w < 2^{31}\)。

i~j的路径上的异或和，就可以表示成根到i的异或和异或上根到j的异或和。

01字典树(Trie),这个东西是解决xor问题的利器.

查找最大异或值的时候我们一般从最高位到低位向下找

只要我的最高位是1,除非你和我的最高位相同,要不然我就是比你大.所以说我们可以贪心的去找当前位^1的节点 建图跑一下dfs求每个节点到根节点的xor值。 构建01Trie去实现我们的贪心即可

0-1字典树

不学这个看不懂题解了（）

算法学习笔记(44): 01字典树 - 知乎 (zhihu.com)

原理很简单，把数字化为二进制后，当作01串，从高位到低位像普通字典树那样存储。例如，如果有数 (1)2,(11)2,(110)2,(111)2 ，存入01字典树就像这样（需要把各个数的位数补成一样多）：

img

尽可能走与该数当前位不同的路径。反之则尽可能走与当前位相同的路径。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include<bits/stdc++.h>
using namespace std;
#define maxn 100008
int trie[maxn*31][2],xo[maxn],ans,rt;
int val[maxn],n,head[maxn],tot;
struct code{int u,v,w;}edge[maxn<<1];
void add(int x,int y,int z)
{
	edge[++tot].u=head[x];
	edge[tot].v=y;
	edge[tot].w=z;
	head[x]=tot;
	edge[++tot].u=head[y];
	edge[tot].v=x;
	edge[tot].w=z;
	head[y]=tot;
}
void build_trie(int x,int rt)
{
	for(int i=1<<30;i;i>>=1)
	{
		bool c=x&i;
		//一个一个存储
		if(!trie[rt][c])trie[rt][c]=++tot;
		rt=trie[rt][c];
	}
	//建树
}
int query(int x,int rt)
{
	int ans=0;
	for(int i=1<<30;i;i>>=1)
	{
		bool c=x&i;
		if(trie[rt][c^1])
		//如果能走反方向要走反方向
		ans+=i,rt=trie[rt][c^1];
		//加上答案
		else rt=trie[rt][c];
	}
	return ans;
}
void dfs(int u,int fa)
{
	for(int i=head[u];i;i=edge[i].u)
	{
		//链式前向星遍历
		if(edge[i].v!=fa)
		{
			//排除自己
			xo[edge[i].v]=xo[u]^edge[i].w;
			//存下来
			dfs(edge[i].v,u);
			//接着搜
		}
	}
}
int main()
{
	cin>>n;
	for(int i=1,u,v,w;i<n;i++)
	{
	cin>>u>>v>>w;
	add(u,v,w);	
	}
	//链式前向星建图
	dfs(1,0);
	//深搜
	for(int i=1;i<=n;i++)
	build_trie(xo[i],rt);
	//插入
	for(int i=1;i<=n;i++)
	//查询
	ans=max(ans,query(xo[i],rt));
cout<<ans;
}

[十二省联考 2019] 异或粽子

题目描述

小粽是一个喜欢吃粽子的好孩子。今天她在家里自己做起了粽子。

小粽面前有 \(n\) 种互不相同的粽子馅儿，小粽将它们摆放为了一排，并从左至右编号为 \(1\) 到 \(n\)。第 \(i\) 种馅儿具有一个非负整数的属性值 \(a_i\)。每种馅儿的数量都足够多，即小粽不会因为缺少原料而做不出想要的粽子。小粽准备用这些馅儿来做出 \(k\) 个粽子。

小粽的做法是：选两个整数数 \(l\), \(r\)，满足 \(1 \leqslant l \leqslant r \leqslant n\)，将编号在 \([l, r]\) 范围内的所有馅儿混合做成一个粽子，所得的粽子的美味度为这些粽子的属性值的异或和。（异或就是我们常说的 xor 运算，即 C/C++ 中的 ˆ 运算符或 Pascal 中的 xor 运算符）

小粽想品尝不同口味的粽子，因此它不希望用同样的馅儿的集合做出一个以上的 粽子。

小粽希望她做出的所有粽子的美味度之和最大。请你帮她求出这个值吧！

输入格式

第一行两个正整数 \(n\), \(k\)，表示馅儿的数量，以及小粽打算做出的粽子的数量。

接下来一行为 \(n\) 个非负整数，第 \(i\) 个数为 \(a_i\)，表示第 \(i\) 个粽子的属性值。 对于所有的输入数据都满足：\(1 \leqslant n \leqslant 5 \times 10^5\), \(1 \leqslant k \leqslant \min\left\{\frac{n(n-1)}{2},2 \times 10^{5}\right\}\), \(0 \leqslant a_i \leqslant 4 294 967 295\)。

输出格式

输出一行一个整数，表示小粽可以做出的粽子的美味度之和的最大值。

样例 #1

样例输入 #1

1
2
3 2
1 2 3

样例输出 #1

1
6

提示

测试点 \(n\) \(k\)
\(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\) \(\leqslant 10^3\) \(\leqslant 10^3\)
\(9\), \(10\), \(11\), \(12\) \(\leqslant 5 \times 10^5\) \(\leqslant 10^3\)
\(13\), \(14\), \(15\), \(16\) \(\leqslant 10^3\) \(\leqslant 2 \times 10^5\)
\(17\), \(18\), \(19\), \(20\) \(\leqslant 5 \times 10^5\) \(\leqslant 2 \times 10^5\)

(在其他都抄完题解后，回来对付3道紫色题目)

康康暴力（）

把每一对的异或值都插入一个大根堆（优先队列）中，然后弹出 �k 次最大值，弹出的所有值的和就是最终答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <bits/stdc++.h>
#define ui unsigned int
#define ull unsigned long long
using namespace std;
const int N = 5e5 + 6;
int n, k;
ui a[N], s[N];
priority_queue<ui> q;
ull ans;

inline ui rd() {
	ui x = 0;
	char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + ch - '0';
		ch = getchar();
	}
	return x;
}

int main() {
	cin >> n >> k;
	for (int i = 1; i <= n; i++) a[i] = rd(), s[i] = s[i-1] ^ a[i];
	for (int l = 1; l <= n; l++)
		for (int r = l; r <= n; r++)
			q.push(s[r] ^ s[l-1]);
	while (k--) ans += q.top(), q.pop();
	cout << ans << endl;
	return 0;
}

区间异或和显然可以转化成两个前缀和的异或，那么现在的问题就变成了求前 k 大的异或对。

由于这里是有序对，我们可以在开头把 k×2 ，最后再让 ans/=2，这样就可以直接统计无序点对了。

容易想到用 Trie 来处理二进制数位。

首先，对于每个右端点，将使异或和取到最大值的左端点位置+异或和放进堆里。

然后，每次显然是取堆顶的一对。考虑如何在取出之后放入该右端点的次大值。

Trie 上不一定只能查询最值！我们也可以在 Trie 上用类似平衡树查询第 p 大的思想来找特定串的第 k 大异或和。

在向 Trie 中插入的时候顺便统计子树大小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include<iostream>
#include<queue>
using ll=long long;
using namespace std;
const int N=20000000+10;
struct Node
{
    int id,rk;long long w;
    bool operator <(const Node &a)const{return w<a.w;}
};
//排序
priority_queue<Node>q;
ll ans=1,x,s[N];
int a[N][2],sze[N],n,m,tot;
//字典树初始化操作
void ins(ll x)
{
    int u=0;
    for(int i=31;i>=0;i--)
    {
        int ch=(x>>i)&1;
        sze[u]++;
        //插入的时候维护子树大小便于处理
        if(!a[u][ch])
            a[u][ch]=++tot;
        u=a[u][ch];
    }
    sze[u]++;
    //个数
}
ll query(ll x,int rk)
{
    int u=0;ll ans=0;
    for(int i=31;i>=0;i--)
    {
        int ch=(x>>i)&1;
        if(!a[u][ch^1])
            u=a[u][ch];
        //如果没有和这一位相异的就直接走
        else if(rk<=sze[a[u][ch^1]])
            //平衡树操作，右边树的所有子树都会比左边大，因为是从高位道低位进行处理的
        //ans|=1ll<<i,计算贡献
        {
            u=a[u][ch^1];
            ans|=1LL<<i;
        }//看一下相异节点的子树大小决定走哪边.和平衡树的操作差不多
        else 
            //不然类似于平衡树的做法，因为这个时候你的排名很大，肯定不在右边，在左边，于是你要减去，然后走左子树，这时候没有贡献
        {
            rk-=sze[a[u][ch^1]];
            u=a[u][ch];
        }
        //并且除此之外你还要继续走
    }
    return ans;
}
int main()
{
    cin>>n>>m;
    m<<=1;//前2k个
    for(int i=1;i<=n;i++)
    {
        cin>>x;
        s[i]=s[i-1]^x;
        //异或和
    }
    for(int i=0;i<=n;i++)
    {
        ins(s[i]);//注意有0
    }
    for(int i=0;i<=n;i++)
    {
        q.push((Node){i,1,query(s[i],1)});
    }//堆中节点存第rk大的s[id]^s[j]
    //先把每个最大的放进去
    for(int i=1;i<=m;i++)
    {
        Node t=q.top();
        //取出最大，待会要把这个点的次大放进去
        ans+=t.w;
        //加上答案，就是统计贡献了
        q.pop();
        //弹出
        if(t.rk<n)
            //排名要小于n
            q.push((Node){t.id,t.rk+1,query(s[t.id],t.rk+1)});
        //放入下一位选手
    }
    cout<<(ans>>1)<<'\n';//最后把答案除以二
    //由于我们统计的是k*2，那么结尾就要÷2
}

[USACO2.3] 最长前缀 Longest Prefix

题目描述

在生物学中，一些生物的结构是用包含其要素的大写字母序列来表示的。生物学家对于把长的序列分解成较短的序列（即元素）很感兴趣。

如果一个集合 \(P\) 中的元素可以串起来（元素可以重复使用）组成一个序列 \(s\) ，那么我们认为序列 \(s\) 可以分解为 \(P\) 中的元素。元素不一定要全部出现（如下例中 BBC 就没有出现）。举个例子，序列 ABABACABAAB 可以分解为下面集合中的元素：{A,AB,BA,CA,BBC}

序列 \(s\) 的前面 \(k\) 个字符称作 \(s\) 中长度为 \(k\) 的前缀。设计一个程序，输入一个元素集合以及一个大写字母序列 ，设 \(s'\) 是序列 \(s\) 的最长前缀，使其可以分解为给出的集合 \(P\) 中的元素，求 \(s'\) 的长度 \(k\)。

输入格式

输入数据的开头包括若干个元素组成的集合 \(O\)，用连续的以空格分开的字符串表示。字母全部是大写，数据可能不止一行。元素集合结束的标志是一个只包含一个 . 的行，集合中的元素没有重复。

接着是大写字母序列 \(s\) ，长度为，用一行或者多行的字符串来表示，每行不超过 \(76\) 个字符。换行符并不是序列 \(s\) 的一部分。

输出格式

只有一行，输出一个整数，表示 S 符合条件的前缀的最大长度。

样例 #1

样例输入 #1

1
2
3
A AB BA CA BBC
.
ABABACABAABC

样例输出 #1

1
11

提示

【数据范围】

对于 \(100\%\) 的数据，\(1\le \text{card}(P) \le 200\)，\(1\le |S| \le 2\times 10^5\)，\(P\) 中的元素长度均不超过 \(10\)。

翻译来自NOCOW

USACO 2.3

用f[i]表示前i个字符是否可以分解为集合中的字符

比较跟他长度相等的

并且用dp数组判断成立性

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
int dp[200005],m;
set<string> s[20];
int main()
{
	string tp;
	while (cin>>tp)
	{
		if (tp==".") break;
		s[tp.size()].insert(tp);//存到他大小的集合中 
		m=max(m,int(tp.size()));
		//记录最大长度
	}
	int i,ans=0;
	dp[0]=1;//初始化 
	string n;
	n=" ";
	while (cin>>tp){
		n=n+tp;//将所有的串合成一个 
	}
	for (i=1;i<n.size();i++)
	{//枚举子串 
		for (int j=min(i,m);j>=1;j--)
		{
			string tt=n.substr(i-j+1,j);//截除子串 
			if (s[tt.size()].count(tt)==1&&dp[i-j]==1)
			{//如果合法 
				ans=i;//必定是最大的 
				dp[i]=1;//本身也合法 
				break;//没必要搜下去了 
			}
		}
	}
	cout<<ans;
}

Test

题面翻译

给定3个字符串s1,s2,s3,试求一个字符串，使s1,s2,s3都是这个字符串的子串，并使这个字符串最短。输出最短字符串的长度l。 s1,s2,s3长度<=100000

Translated by 稀神探女

题目描述

Sometimes it is hard to prepare tests for programming problems. Now Bob is preparing tests to new problem about strings — input data to his problem is one string. Bob has 3 wrong solutions to this problem. The first gives the wrong answer if the input data contains the substring $ s_{1} $ , the second enters an infinite loop if the input data contains the substring $ s_{2} $ , and the third requires too much memory if the input data contains the substring $ s_{3} $ . Bob wants these solutions to fail single test. What is the minimal length of test, which couldn't be passed by all three Bob's solutions?

输入格式

There are exactly 3 lines in the input data. The $ i $ -th line contains string $ s_{i} $ . All the strings are non-empty, consists of lowercase Latin letters, the length of each string doesn't exceed $ 10^{5} $ .

输出格式

Output one number — what is minimal length of the string, containing $ s_{1} $ , $ s_{2} $ and $ s_{3} $ as substrings.

样例 #1

样例输入 #1

1
2
3
ab
bc
cd

样例输出 #1

1
4

样例 #2

样例输入 #2

1
2
3
abacaba
abaaba
x

样例输出 #2

1
11

求出能不能包含，不能的话康康相交，再不能就相切罢

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
#include<bits/stdc++.h>
#define min(a,b) ((a)<(b))?(a):(b)
using namespace std;
const int INF=2147483646;
int nxt[4][100050],l[4];
string s[4];
//求出三个字符串的next数组 
void Pre()
{
    for(int f=1;f<4;++f)
    {
        int p=0,len=l[f];
        for(int i=2;i<=len;++i)
		{
            while(p&&s[f][i]!=s[f][p+1]) 
			p=nxt[f][p];
            if(s[f][i]==s[f][p+1]) 
			++p;
            nxt[f][i]=p;
        }
    }
    return ;
}

int f(int a,int b,int c)
{ 
//计算b是不是a的子串
    int ans=INF,p1=0;
    int al=l[a],bl=l[b],cl=l[c];
    for(int i=1;i<=al;++i)
    {
        while(p1&&s[b][p1+1]!=s[a][i]) 
		p1=nxt[b][p1];
        if(s[b][p1+1]==s[a][i]) 
		++p1;
        if(p1==bl)
		{
            p1=-1;//-1代表b是a的子串 
            break;
        }
    }
    
    if(p1==-1)
    {
	//如果b是a的子串，就直接让c和a匹配
        int p=0;
        for(int i=1;i<=al;++i)
		{
            while(p&&s[c][p+1]!=s[a][i]) 
			p=nxt[c][p];
            if(s[c][p+1]==s[a][i]) ++p;
            if(p==cl)
			{
                p=-1;
                break;
            }
        }
        if(p==-1) ans=al;
        //成功了，证明2个都是，直接输出a1
        else ans=al+cl-p;
        //失败了，但是b依然是a的子串，这时候合并进去，只需要算a和c
        //刚刚a和c进行了匹配，因此可以计算出来
    }
    else
    {
    	//否则，先用c匹配a再从a，b相交位置开始匹配b 
        int p=0;
        for(int i=1;i<=al;++i)
		{
            while(p&&s[c][p+1]!=s[a][i]) 
			p=nxt[c][p];
            if(s[c][p+1]==s[a][i]) 
			++p;
            if(p==cl)
            {
                p=-1;
                break;
            }
        }
        if(p!=-1)
		{
			//c不是a的子串，匹配c和b
            int p2=p;
            for(int i=p1+1;i<=bl;++i)
			{
                while(p2&&s[c][p2+1]!=s[b][i]) 
				p2=nxt[c][p2];
                if(s[c][p2+1]==s[b][i]) 
				++p2;
                if(p2==cl)
				{
                    p2=-1;
                    break;
                }
            }
            if(p2==-1) 
			ans=al+bl-p1;
            //c是b的子串，b不是a的子串
            //因此同理计算
            else 
			ans=al+bl-p1 + cl -p2;
            //三个都不是，直接这样算
        }
        else 
		ans=al+bl-p1;
        //不然就是了，c是b的子串
    }
    return ans;
}
int main(){
    cin>>s[1]>>s[2]>>s[3];
    s[1]=" "+s[1];
    s[2]=" "+s[2];
    s[3]=" "+s[3];
    int ans=INF;
    l[1]=s[1].length()-1;
	l[2]=s[2].length()-1;
	l[3]=s[3].length()-1;
    //预处理和求Next
    Pre();
    //进行结果计算
    ans=min(ans,f(1,2,3));
    ans=min(ans,f(1,3,2));
    ans=min(ans,f(2,1,3));
    ans=min(ans,f(2,3,1));
    ans=min(ans,f(3,2,1));
    ans=min(ans,f(3,1,2));
    //真·暴力枚举排列顺序 
	cout<<ans;
}

[POI2006] OKR-Periods of Words

题面翻译

对于一个仅含小写字母的字符串 \(a\)，\(p\) 为 \(a\) 的前缀且 \(p\ne a\)，那么我们称 \(p\) 为 \(a\) 的 proper 前缀。

规定字符串 \(Q\) 表示 \(a\) 的周期，当且仅当 \(Q\) 是 \(a\) 的 proper 前缀且 \(a\) 是 \(Q+Q\) 的前缀。若这样的字符串不存在，则 \(a\) 的周期为空串。

例如 ab 是 abab 的一个周期，因为 ab 是 abab 的 proper 前缀，且 abab 是 ab+ab 的前缀。

求给定字符串所有前缀的最大周期长度之和。

题目描述

A string is a finite sequence of lower-case (non-capital) letters of the English alphabet. Particularly, it may be an empty sequence, i.e. a sequence of 0 letters. By A=BC we denotes that A is a string obtained by concatenation (joining by writing one immediately after another, i.e. without any space, etc.) of the strings B and C (in this order). A string P is a prefix of the string !, if there is a string B, that A=PB. In other words, prefixes of A are the initial fragments of A. In addition, if P!=A and P is not an empty string, we say, that P is a proper prefix of A.

A string Q is a period of Q, if Q is a proper prefix of A and A is a prefix (not necessarily a proper one) of the string QQ. For example, the strings abab and ababab are both periods of the string abababa. The maximum period of a string A is the longest of its periods or the empty string, if A doesn't have any period. For example, the maximum period of ababab is abab. The maximum period of abc is the empty string.

Task Write a programme that:

reads from the standard input the string's length and the string itself,calculates the sum of lengths of maximum periods of all its prefixes,writes the result to the standard output.

输入格式

In the first line of the standard input there is one integer \(k\) (\(1\le k\le 1\ 000\ 000\)) - the length of the string. In the following line a sequence of exactly \(k\) lower-case letters of the English alphabet is written - the string.

输出格式

In the first and only line of the standard output your programme should write an integer - the sum of lengths of maximum periods of all prefixes of the string given in the input.

样例 #1

样例输入 #1

1
2
8
babababa

样例输出 #1

1
24

解释：假设有一个序列s

从1,2.....i

然后有一个j,满足(1≤j≤i)，

故后者是前者的前缀

又1，2....i是1......j ,1.....j的前缀

那么j+1,....i必须是1....j的前缀

所以说j+1....i又是1....i的后缀

因此j+1....i是1.....i的公共前后缀

KMP可以求出来j

又因为要序列尽可能大，就是j尽可能小罢，那么这个周期就会大起来

中间需要记忆化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=1e6+10;
int pmt[N];
ll ans;
inline void get_pmt(const string &s)
{
    for(int i=1,j=0;i<s.length();i++){
        while(j&&s[i]!=s[j])j=pmt[j-1];
        if(s[i]==s[j])j++;
        pmt[i]=j;
    }
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin>>n;
    string s;
    cin>>s;
    get_pmt(s);
    int j=0;
    for(int i=0;i<s.length();i++){
        j=i+1;
        while(pmt[j-1])j=pmt[j-1];
        if(pmt[i])pmt[i]=j;
        ans+=i-j+1;
    }
    cout<<ans;
    return 0;
}

[NOI2014] 动物园

题目描述

近日，园长发现动物园中好吃懒做的动物越来越多了。例如企鹅，只会卖萌向游客要吃的。为了整治动物园的不良风气，让动物们凭自己的真才实学向游客要吃的，园长决定开设算法班，让动物们学习算法。

某天，园长给动物们讲解 KMP 算法。

园长：“对于一个字符串 \(S\)，它的长度为 \(L\)。我们可以在 \(O(L)\) 的时间内，求出一个名为 \(\mathrm{next}\) 的数组。有谁预习了 \(\mathrm{next}\) 数组的含义吗？”

熊猫：“对于字符串 \(S\) 的前 \(i\) 个字符构成的子串，既是它的后缀又是它的前缀的字符串中（它本身除外），最长的长度记作 \(\mathrm{next}[i]\)。”

园长：“非常好！那你能举个例子吗？”

熊猫：“例 \(S\) 为 \(\verb!abcababc!\)，则 \(\mathrm{next}[5]=2\)。因为\(S\)的前\(5\)个字符为 \(\verb!abcab!\)，\(\verb!ab!\) 既是它的后缀又是它的前缀，并且找不到一个更长的字符串满足这个性质。同理，还可得出 \(\mathrm{next}[1] = \mathrm{next}[2] = \mathrm{next}[3] = 0\)，\(\mathrm{next}[4] = \mathrm{next}[6] = 1\)，\(\mathrm{next}[7] = 2\)，\(\mathrm{next}[8] = 3\)。”

园长表扬了认真预习的熊猫同学。随后，他详细讲解了如何在 \(O(L)\) 的时间内求出 \(\mathrm{next}\) 数组。

下课前，园长提出了一个问题：“KMP 算法只能求出 \(\mathrm{next}\) 数组。我现在希望求出一个更强大 \(\mathrm{num}\) 数组一一对于字符串 \(S\) 的前 \(i\) 个字符构成的子串，既是它的后缀同时又是它的前缀，并且该后缀与该前缀不重叠，将这种字符串的数量记作 \(\mathrm{num}[i]\)。例如 \(S\) 为 \(\verb!aaaaa!\)，则 \(\mathrm{num}[4] = 2\)。这是因为\(S\)的前 \(4\) 个字符为 \(\verb!aaaa!\)，其中 \(\verb!a!\) 和 \(\verb!aa!\) 都满足性质‘既是后缀又是前缀’，同时保证这个后缀与这个前缀不重叠。而 \(\verb!aaa!\) 虽然满足性质‘既是后缀又是前缀’，但遗憾的是这个后缀与这个前缀重叠了，所以不能计算在内。同理，\(\mathrm{num}[1] = 0,\mathrm{num}[2] = \mathrm{num}[3] = 1,\mathrm{num}[5] = 2\)。”

最后，园长给出了奖励条件，第一个做对的同学奖励巧克力一盒。听了这句话，睡了一节课的企鹅立刻就醒过来了！但企鹅并不会做这道题，于是向参观动物园的你寻求帮助。你能否帮助企鹅写一个程序求出\(\mathrm{num}\)数组呢？

特别地，为了避免大量的输出，你不需要输出 \(\mathrm{num}[i]\) 分别是多少，你只需要输出所有 \((\mathrm{num}[i]+1)\) 的乘积，对 \(10^9 + 7\) 取模的结果即可。

输入格式

第 \(1\) 行仅包含一个正整数 \(n\)，表示测试数据的组数。
随后 \(n\) 行，每行描述一组测试数据。每组测试数据仅含有一个字符串 \(S\)，\(S\) 的定义详见题目描述。数据保证 \(S\) 中仅含小写字母。输入文件中不会包含多余的空行，行末不会存在多余的空格。

输出格式

包含 \(n\) 行，每行描述一组测试数据的答案，答案的顺序应与输入数据的顺序保持一致。对于每组测试数据，仅需要输出一个整数，表示这组测试数据的答案对 \(10^9+7\) 取模的结果。输出文件中不应包含多余的空行。

样例 #1

样例输入 #1

1
2
3
4
3
aaaaa
ab
abcababc

样例输出 #1

1
2
3
36
1
32

提示

测试点编号 约定
1 \(n \le 5, L \le 50\)
2 \(n \le 5, L \le 200\)
3 \(n \le 5, L \le 200\)
4 \(n \le 5, L \le 10,000\)
5 \(n \le 5, L \le 10,000\)
6 \(n \le 5, L \le 100,000\)
7 \(n \le 5, L \le 200,000\)
8 \(n \le 5, L \le 500,000\)
9 \(n \le 5, L \le 1,000,000\)
10 \(n \le 5, L \le 1,000,000\) 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
//num的定义：不互相重叠的公共前后缀个数
//num不同于next记录的是一个最大值，它记录的是一个和值    
//考虑一个前缀的next[i]，那么next[i]，next[next[i]]，next[next[next[i]]]......都是这个前缀串i的公共前后缀
#include<bits/stdc++.h>
using namespace std;
const int N=1000010;
const int mod=1e9+7;
int n,t;
int nxt[N],num[N];
long long ans;
string s;
int main()
{
    cin>>t;
    while(t--)
    {
        ans=1;num[1]=1;
        cin>>s;
		s=" "+s;
		n=s.length()-1;
       for(int i=2,j=0;i<=n;i++)
    {
        while(j&&s[i]!=s[j+1]) j=nxt[j];
        if(s[i]==s[j+1]) 
		j++;
        nxt[i]=j;
       num[i]=num[j]+1;
           //求解个数的过程
    }
  for(int i=2,j=0;i<=n;i++)
    {
        while(j&&s[i]!=s[j+1]) j=nxt[j];
      //不断回溯
        if(s[i]==s[j+1])j++;
        while((j<<1)>i) j=nxt[j];
      //不断回溯，不然重叠
        ans=(ans*1ll*(num[j]+1))%mod;
    }
        cout<<ans<<'\n';
    }
    return 0;
}

[USACO08DEC] Secret Message G

题目描述

Bessie is leading the cows in an attempt to escape! To do this, the cows are sending secret binary messages to each other.

Ever the clever counterspy, Farmer John has intercepted the first \(b_i\) (\(1 \le b_i \le 10,000\)) bits of each of \(M\) (\(1 \le M \le 50,000\)) of these secret binary messages.

He has compiled a list of \(N\) (\(1 \le N \le 50,000\)) partial codewords that he thinks the cows are using. Sadly, he only knows the first \(c_j\) (\(1 \le c_j \le 10,000\)) bits of codeword \(j\).

For each codeword \(j\), he wants to know how many of the intercepted messages match that codeword (i.e., for codeword \(j\), how many times does a message and the codeword have the same initial bits). Your job is to compute this number.

The total number of bits in the input (i.e., the sum of the \(b_i\) and the \(c_j\)) will not exceed \(500,000\).

贝茜正在领导奶牛们逃跑．为了联络，奶牛们互相发送秘密信息．

信息是二进制的，共有 \(M\)（\(1 \le M \le 50000\)）条，反间谍能力很强的约翰已经部分拦截了这些信息，知道了第 \(i\) 条二进制信息的前 \(b_i\)（\(1 \le b_i \le 10000\)）位，他同时知道，奶牛使用 \(N\)（\(1 \le N \le 50000\)）条暗号．但是，他仅仅知道第 \(j\) 条暗号的前 \(c_j\)（\(1 \le c_j \le 10000\)）位。

对于每条暗号 \(j\)，他想知道有多少截得的信息能够和它匹配。也就是说，有多少信息和这条暗号有着相同的前缀。当然，这个前缀长度必须等于暗号和那条信息长度的较小者。

在输入文件中，位的总数（即 \(\sum b_i + \sum c_i\)）不会超过 \(500000\)。

输入格式

Line \(1\): Two integers: \(M\) and \(N\).

Lines \(2 \ldots M+1\): Line \(i+1\) describes intercepted code \(i\) with an integer \(b_i\) followed by \(b_i\) space-separated 0's and 1's.

Lines \(M+2 \ldots M+N+1\): Line \(M+j+1\) describes codeword \(j\) with an integer \(c_j\) followed by \(c_j\) space-separated 0's and 1's.

输出格式

Lines \(1 \ldots N\): Line \(j\): The number of messages that the \(j\)-th codeword could match.

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
10
4 5 
3 0 1 0 
1 1 
3 1 0 0 
3 1 1 0 
1 0 
1 1 
2 0 1 
5 0 1 0 0 1 
2 1 1

样例输出 #1

1
2
3
4
5
1 
3 
1 
1 
2

提示

Four messages; five codewords.

The intercepted messages start with 010, 1, 100, and 110.

The possible codewords start with 0, 1, 01, 01001, and 11.

0 matches only 010: 1 match

1 matches 1, 100, and 110: 3 matches

01 matches only 010: 1 match

01001 matches 010: 1 match

11 matches 1 and 110: 2 matches

枚举会TLE，这里可以用 字典树

因为输入的只有0和1，所以可以用bool做

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include<bits/stdc++.h>
using namespace std;
const int N=500001;
int n,m,k,ch[N][3],tot=1,bo[N],sum[N],x;
bool p[N];
///ch[u][i]表示节点u的i字符指针指向的节点，若值为0，表示没有这个节点
void add(bool p[]) 
{
    //插入字符串
	int u=1;
	for(int i=1; i<=k; i++) 
    {
		int c=p[i];
		if(ch[u][c]==-1)
            ch[u][c]=++tot;
		u=ch[u][c];///它指向它的子节点
		sum[u]++;///经过该节点字符串个数
	}
	bo[u]++;///该字符串以u结尾
}

int find(bool p[])
{
	int u=1;
	int res=0;
	for(int i=1; i<=k; i++) 
    {
		int c=p[i];
		if(ch[u][c]==-1)return res;
		u=ch[u][c];
		res+=bo[u];
        //加上与当前节点为结束的个数
	}
	return res-bo[u]+sum[u];//加上前缀相同且长度比它长的字符串个数
    //因为必须等于较短者
}
int main() 
{
	int x;
	cin>>m>>n;
	memset(ch,-1,sizeof ch);
	for(int i=1; i<=m; i++)
    {
		cin>>k;
		for(int j=1; j<=k; j++) 
        {
			cin>>p[j];
		}
		add(p);
	}
	for(int i=1; i<=n; i++) 
    {
		cin>>k;
		for(int j=1; j<=k; j++) 
        {
			cin>>p[j];
		}
		cout<<find(p)<<'\n';
	}
}

最大异或和

题目描述

给定一个非负整数序列 \(\{a\}\)，初始长度为 \(N\)。

有 \(M\) 个操作，有以下两种操作类型：

  1. A x：添加操作，表示在序列末尾添加一个数 \(x\)，序列的长度 \(N\) 加 \(1\)。
  2. Q l r x：询问操作，你需要找到一个位置 \(p\)，满足 \(l \le p \le r\)，使得：\(a[p] \oplus a[p+1] \oplus ... \oplus a[N] \oplus x\) 最大，输出最大值。

输入格式

第一行包含两个整数 \(N, M\)，含义如问题描述所示。
第二行包含 \(N\) 个非负整数，表示初始的序列 \(A\)。
接下来 \(M\) 行，每行描述一个操作，格式如题面所述。

输出格式

假设询问操作有 \(T\) 个，则输出应该有 \(T\) 行，每行一个整数表示询问的答案。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
5 5
2 6 4 3 6
A 1 
Q 3 5 4 
A 4
Q 5 7 0 
Q 3 6 6

样例输出 #1

1
2
3
4
5
6

提示

  • 对于所有测试点，\(1\le N,M \le 3\times 10 ^ 5\)，\(0\leq a_i\leq 10 ^ 7\)。

进入持久化字典树的领域了（）

于是开始重头学习字典树：

字典树例题

Phone List

题面翻译

给定\(n\)个长度不超过\(10\)的数字串，判断是否有两个字符串\(A\)和\(B\),满足\(A\)是\(B\)的前缀，若有，输出NO，若没有，输出YES。

Translated by @wasa855

题目描述

PDF

输入格式

输出格式

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
10
11
2
3
911
97625999
91125426
5
113
12340
123440
12345
98346

样例输出 #1

1
2
NO
YES
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//快排做法
#include<bits/stdc++.h>
using namespace std;
string s[10001];
int main()
{
    int k,n;
	cin>>k;
    while(k--)
    {
        bool flag=false;
        cin>>n;
        for(int i=1;i<=n;i++)
            cin>>s[i];
        sort(s+1,s+n+1);//快排神通，将字符串排序
        for(int i=1;i<=n-1;i++)
        {
            if(s[i+1].find(s[i],0)==0)
            {
                flag=true;
                break;
            }
        }
        if(flag) cout<<"NO"<<'\n';
        else cout<<"YES"<<'\n';
    }
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
//字典树做法
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
const int Z=10;
int T,n,tot;
int ch[N][Z];						//储存trie树
bool bo[N];
char s[20];
bool insert(char *s)					//插入字符串
{
	int len=strlen(s);
	int u=1;
	bool flag=false;
	for (int i=0;i<len;++i)
	{
		int c=s[i]-'0';
		if (!ch[u][c])
		{
			ch[u][c]=++tot;
		}
		else if (i==len-1) //当前串一定是之前某个串的前缀
		{
			flag=true;			//没有插入任何新结点
			return flag;
		}
		u=ch[u][c];
		if (bo[u])//之前插入的某个串是当前串的前缀。
		{
			flag=true;			//经过某个有标记的结点
			return flag;
		}
	}
	bo[u]=true;
	return flag;
}
int main()						
{
	cin>>T;
	while (T--)
	{
		cin>>n;
		tot=1;
		memset(ch,0,sizeof(ch));
		memset(bo,false,sizeof(bo));
		bool ans=false;
		for (int i=1;i<=n;++i)
		{
			cin>>s;
			if (insert(s))
			{
				ans=true;
			}
		}
		if (!ans)
		{
			puts("YES");
		}
		else
		{
			puts("NO");
		}
	}
	return 0;
}

01-字典树

01字典树的一个功能是：

  1. 向当前集合中插入一个正整数。

  2. 查询当前集合中异或上x后最大的那个数。

  3. 插入x，我们把x看做一个二进制数，从高位向低位遍历，根据当前位是0或者1，把Tire的枝叶伸向不同的方向。

  4. 根据异或的性质，我们同样是从高位到低位遍历x的二进制串，若x当前位为1且存在0的枝叶，那就去0那一条枝叶，总之就是尽量与x的当前位取反，这样可以贪心的得到正解。

如果我想查询区间 [l,r] 的数字与x异或后最大的那个数--可持久化字典树

当我们需要保存一个数据结构不同时间的每个版本,最朴素的方法就是每个时间都创建一个独立的数据结构,单独储存。

但是这种方法不仅每次复制新的数据结构需要时间，空间上也受不了储存这么多版本的数据结构。

然而有一种叫git的工具，可以维护工程代码的各个版本，而空间上也不至于十分爆炸。怎么做到呢？

答案是版本分支，即每次创建新的版本不完全复制老的数据结构，而是在老的数据结构上加入不同版本的分支。

太生动形象了

还有两道题，励志用持久化字典树解决（）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
#include <bits/stdc++.h>
using namespace std;
const int N = 2 * (3e5 + 10);   
// 注意题目中存在添加操作，添加操作最多也有 N 次，最终存在的数字个数最多是两倍的 N
const int L = 25;               
// 每一个数字的二进制长度
int n, m;
int sum[N];         
// sum[i] 表示从 0~i 的数字的 异或前缀和
int trie[L * N][2]; 
// 字典树的邻接矩阵
int cnt;            
// 用于分配新结点的变量
int root[N];        
// root[i] 为版本为 i 的字典树的根结点编号
int ver[L * N];     
// 存每一个结点的版本编号
/*
可持久化字典树插入操作，新建一个版本编号为 ver_in 的字典树，并将新的数字插入到新版本的字典树中
x 表示当前版本的根结点编号，y 表示上一版本的根结点编号，val 为要插入的数字，ver_in 为当前新建的字典树的版本编号
*/
void insert(int x, int y, int val, int ver_in)
{
    int ch;
    ver[x] = ver_in;   
    //记录本次编号
    //然后当前这个值就
    // 根结点编号为本次要新建的字典树的版本编号
    for (int i = L - 1; ~i; i--)        
        // 从高到低遍历待插入数字的每一位
    {
        ch = (val >> i & 1);
        trie[x][ch] = ++cnt;            
        // 与当前位相同的边，新建一个结点并连上，这样新插入的数字版本号就能与新建的字典树保持一致
        trie[x][!ch] = trie[y][!ch];    
        // 与当前位不同的边，连到上一个版本的对应边上
        x = trie[x][ch];               
        y = trie[y][ch];
         // 两个结点都往与当前位相同的边上走
        ver[x] = ver_in;                
        // 新建结点的版本号与当前字典树版本号保持一致
    }
}
/*
可持久化字典树查询操作，代入的 t 是开始查询时的，对应版本的字典树的根结点
从根结点为 t 的字典树上开始查询，查询过程中不能走到版本号 < l 的结点上
查询过程中以 tar 作为指导，找到查询范围内的数字与 tar 异或后得到的最大值，并返回
*/
int query(int t, int l, int tar)
{
    int ch;
    int cur = t;    
    // 当前结点初始化为开始查询的根结点编号
    int res = 0;    
    // 结果初始化为 0
    for (int i = L - 1; ~i; i--)        
        // 从高到低遍历 tar 的每一位
    {
        ch = (tar >> i & 1);
        // 基于贪心思想，如果与当前位不同的边，所连向的结点的版本号 >= 设定的左边界，则往这条边上走
        // （由于 0 号结点，即空结点的版本号被设为了 -1，此处不可能会走到空结点上）
        if (ver[trie[cur][!ch]] >= l)
        {
            res |= (1 << i);            
            // 走了与当前位不同的边，结果代表异或值，结果的这一位就可以设为 1
            cur = trie[cur][!ch];       // 移动当前结点
        }
        else cur = trie[cur][ch];       
        // 否则只能往与当前位相同的边上走，不产生贡献
    }
    return res;     
    // 返回结果
}
int main(void)
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> m;
    ver[0] = -1;    
    // 将空结点版本号设置为 -1，可以简化查询操作中的判断条件
    root[0] = ++cnt;            
    // 为 0 号字典树的根结点分配新结点
    insert(root[0], 0, 0, 0);   
    // 在 0 号字典树内插入数字 0，对应 sum[0]（由于没有前一个版本，参数 y 直接代入空结点）
    for (int i = 1; i <= n; i++)
    {
        cin >> sum[i];
        sum[i] ^= sum[i - 1];   
        // 获得异或前缀和
        root[i] = ++cnt;                            
        // 为 i 号字典树的根结点分配新结点
        insert(root[i], root[i - 1], sum[i], i);    
        // 把 sum[i] 插入到 i 号字典树中
    }
    char opt;
    int l, r, x;
    while (m--)
    {
        cin >> opt;
        switch (opt)
        {
        // 操作 1，添加操作，需要新建一棵字典树
        case 'A':
            n++;                    
                // 新插入了一个数字，n 的值对应增加
            cin >> sum[n];
            sum[n] ^= sum[n - 1];   
                // 得到异或前缀和
            root[n] = ++cnt;                            
                // 为新版本的字典树分配根结点
            insert(root[n], root[n - 1], sum[n], n);    
                // 把新得到的异或前缀和，插入到新版本的字典树内
            break;
        // 操作 2，询问操作
        case 'Q':
            cin >> l >> r >> x;
            x ^= sum[n];            
                // x xor sum[n] 就是查询时的引导值，要得到在查询范围内与这个值异或后最大的结果
            cout << query(root[r - 1], l - 1, x) << '\n';   
                // 查询要进入的字典树，版本号为 r-1，查询过程中不能走到 l-1 以前的版本
            break;
        }
    }
}

【模板】普通平衡树

题目描述

您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

  1. 插入一个数 \(x\)。
  2. 删除一个数 \(x\)（若有多个相同的数，应只删除一个）。
  3. 定义排名为比当前数小的数的个数 \(+1\)。查询 \(x\) 的排名。
  4. 查询数据结构中排名为 \(x\) 的数。
  5. 求 \(x\) 的前驱（前驱定义为小于 \(x\)，且最大的数）。
  6. 求 \(x\) 的后继（后继定义为大于 \(x\)，且最小的数）。

对于操作 3,5,6，不保证当前数据结构中存在数 \(x\)。

输入格式

第一行为 \(n\)，表示操作的个数,下面 \(n\) 行每行有两个数 \(\text{opt}\) 和 \(x\)，\(\text{opt}\) 表示操作的序号（$ 1 $）

输出格式

对于操作 \(3,4,5,6\) 每行输出一个数，表示对应答案。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
10
11
10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598

样例输出 #1

1
2
3
106465
84185
492737

提示

【数据范围】
对于 \(100\%\) 的数据，\(1\le n \le 10^5\)，\(|x| \le 10^7\)

来源：Tyvj1728 原名：普通平衡树

在此鸣谢

Splay算法

splay tree，中文名伸展树。

其是一种自平衡二叉排序树，通过其特有的splay操作，可以使得整棵树在维持二叉排序树性质的情况下，又不至于退化为链。

splay树支持对数据进行查询、插入、删除等操作，且各操作的时间复杂度摊还后皆是 O(logn) ，是一种相对高效的数据结构。

Splay树并不在乎二叉排序树是否时刻平衡，而是通过在每次操作时进行微调来使得树趋于平衡。

每当我们对二叉排序树进行一次操作（查询、插入、删除等）时，我们就将操作的节点通过旋转操作挪到根节点上，并且使得整棵树依旧满足二叉排序树的性质，这一系列过程我们称之为splay操作。

旋转的例子：

现在我们的现在目标只有一个x节点往上面爬,爬到它原本的父亲节点y,然后让y节点下降 首先思考BST性质,那就是右子树上的点,统统都比父亲节点大对不对,现在我们的x节点是父亲节点y的左节点,也就是比y节点小. 那么我们为了不改变答案顺序,我们可以让y节点成为x节点的右儿子,也就是y节点仍然大于我们的x节点 这么做当然是没有问题的,那么我们现在又有一个问题了,x节点的右子树原来是有子树B的,那么如果说现在y节点以及它的右子树(没有左子树,因为曾经x节点是它的左子树),放到了x节点的右子树上,那么岂不是多了什么吗? 我们知道 x节点的右子树必然是大于x节点的,然后y节点必然是大于x节点的右子树和x节点的,因为x节点和它的右子树都是在y节点的左子树,都比它小 既然如此的话,我们为什么不把x节点原来的右子树,放在节点y的左子树上面呢?这样的话,我们就巧妙地避开了冲突,达成了x节点上移,y节点下移.

通解：

  1. 那么y节点就放到x节点的z^1的位置.(也就是,x节点为y节点的右子树,那么y节点就放到左子树,x节点为y节点左子树,那么y节点就放到右子树位置,这样就完美满足条件)
  2. 如果说x节点的z1的位置上,已经有节点,或者一棵子树,那么我们就将原来x节点z1位置上的子树,放到y节点的位置z上面.

由于一直旋转一个点是不行的，也会导致算法失败，

因此，引入双旋操作

  1. 如果当前处于共线状态的话,那么先旋转y,再旋转x.这样可以强行让他们不处于共线状态,然后平衡这棵树.
  2. 如果当前不是共线状态的话,那么只要旋转x即可.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
#include<bits/stdc++.h>
using namespace std;
const int maxn = 5e5+10;
const int Inf = 2147483647;
struct Node
{
       int ch[2];//子节点
       int fa;//父节点 
       int cnt;//数量
       int val;//值 
       int son;//儿子数量  
}t[maxn];

int n,tot,root;
void pushup(int x){
	t[x].son = t[t[x].ch[0]].son+t[t[x].ch[1]].son+t[x].cnt;
}
void rotate(int x)
{//旋转
	int y=t[x].fa;//当前节点的父亲
	int z=t[y].fa;//
	int k=t[y].ch[1]==x;//找到x是y的左还是右节点，便于进行上文中所说操作
    //如果k=1，那么是右节点
    //不然是左节点
	t[z].ch[t[z].ch[1]==y]=x;//以下都是上边说过的操作。
	t[x].fa=z;//改变x的父亲，y->z
	t[y].ch[k]=t[x].ch[k^1];//y则是继承x的儿子，和自己方向不是一边的
	t[t[x].ch[k^1]].fa=y;//继承的儿子和自己方向不一样，要改变一下父亲
	t[x].ch[k^1]=y;//接上方向不一样的
	t[y].fa=x;//Y的父亲变成x
	pushup(y);//开始Pushup
	pushup(x);//开始Pushup
}
void splay(int x,int goal){//旋转
	while(t[x].fa!=goal){//父亲节点不是目标
		int y=t[x].fa;
		int z=t[y].fa;
        ////父节点祖父节点
		if(z!=goal)
        {//爷爷节点也不是目标
			(t[y].ch[0]==x)^(t[z].ch[0]==y)?rotate(x):rotate(y);//y左儿子是x就翻转x，不然翻转y（因为树有序，不能破坏性质）
		}
		rotate(x);
	}
	if(goal == 0){//到了根节点的话让根节点更新
		root = x;
	}
}
/*
从根节点开始，左侧都比他小，右侧都比他大，
所以只需要相应的往左/右递归
如果当前位置的val已经是要查找的数
那么直接把他Splay到根节点，方便接下来的操作
类似于二分查找，
所以时间复杂度O(logn)
*/
void Find(int x)//查找x的位置，并将其旋转到根节点
{
	int u=root;//从根开始
	if(!u)return;//没有树就直接跳出
	while(t[u].ch[x>t[u].val] && x!=t[u].val){//依次向下找到当前值的点
		u=t[u].ch[x>t[u].val];//更新
	}
	splay(u,0);//旋转
}

/*
往Splay中插入一个数
类似于Find操作，只是如果是已经存在的数，就可以直接在查找到的节点的进行计数
如果不存在，在递归的查找过程中，会找到他的父节点的位置，
然后就会发现底下没有啦。。。
所以这个时候新建一个节点就可以了
*/
void Add(int x){
	int u=root,fa=0;
	while(u&&t[u].val!=x){
		fa=u;
		u=t[u].ch[x>t[u].val];
	}
	if(u){//有的话直接大小加一
		t[u].cnt++;
	}
	else{//没有该值的节点
		u=++tot;
		if(fa)t[fa].ch[x>t[fa].val]=u;
		t[tot].ch[1]=0;
		t[tot].ch[0]=0;//不存在两个儿子
		t[tot].val=x;//值
		t[tot].fa=fa;//父节点
		t[tot].cnt=1;//数量
		t[tot].son=1;//大小
	}
	splay(u,0);////把当前位置移到根，保证结构的平衡
}
/*
首先就要执行Find操作
把要查找的数弄到根节点
然后，以前驱为例
先确定前驱比他小，所以在左子树上
然后他的前驱是左子树中最大的值
所以一直跳右结点，直到没有为止
找后继反过来就行了
*/
int Fr_last(int x,int flag)
{
    //前驱flag为0,后继为1
	Find(x);//找到位置
	int u=root;//根开始
	if((t[u].val>x&&flag) || (t[u].val<x && !flag))
    {//当前点满足就直接返回
		return u;
	}
	u=t[u].ch[flag];//向目标点（左或右）转移
	while(t[u].ch[flag^1])u=t[u].ch[flag^1];//找到转移后最接近当前值的点
	return u;//返回
}

void Delete(int x){
	int Front=Fr_last(x,0);//前驱
	int Last=Fr_last(x,1);//后继
	splay(Front,0);//旋转
	splay(Last,Front);
      //将前驱旋转到根节点，后继旋转到根节点下面
    //很明显，此时后继是前驱的右儿子，x是后继的左儿子，并且x是叶子节点
	int del=t[Last].ch[0];//找到需要删除的点
	if(t[del].cnt>1){//大于1直接减
		t[del].cnt--;
		splay(del,0);
	}
	else{//否则直接删除
		t[Last].ch[0]=0;
	}
}

int Find_thval(int x){
	int u=root;//根开始
	if(t[u].son<x){//如果没有这么多，直接返回0
		return 0;
	}
	while(666666){//一直循环
		int y=t[u].ch[0];//记录左儿子
		if(x>t[y].son+t[u].cnt)
        {//排名大就减去，然后走到右节点
			x-=t[y].son+t[u].cnt;
			u=t[u].ch[1];
		}
		else{
			if(x<=t[y].son){//否则走到左节点
				u=y;
			}
			else return t[u].val;//如果排名比上边的小，且比左节点的值大，这就是满足的价值，直接返回
		}
	}
}

int main(){
	int n;
	Add(Inf);
	Add(-Inf);
	cin>>n;
	while(n--){
		int opt;
		cin>>opt;
		int x;
		if(opt == 1){
			cin>>x;
			Add(x);
		}//插入
		if(opt == 2){
			cin>>x;
			Delete(x);
		}
        //删除
		if(opt == 3){
			cin>>x;
			Find(x);
            //查找x的排名
			int ans = t[t[root].ch[0]].son + (t[root].val < x ? t[root].cnt : 0);
            //加上数量
			cout<<ans<<'\n';
		}
		if(opt == 4){
			int ans;
			cin>>x;
			ans = Find_thval(x+1);
			cout<<ans<<'\n';
		}
		if(opt == 5){
			cin>>x;
			int ans = Fr_last(x,0);
			cout<<t[ans].val<<'\n';
		}
		if(opt == 6){
			cin>>x;
			int ans = Fr_last(x,1);
			cout<<t[ans].val<<'\n';
		}
	}
    //0是查前驱，1是查后继
	return 0;
}

「EZEC-4」可乐

题目背景

很久以前，有一个 pigstd，非常迷恋美味的可乐。为了得到美味的可乐，他几乎用尽了所有的钱，他甚至对自己的 npy 也漠不关心其实是因为他没有npy，更不爱好看戏。除非买了新可乐，才会坐上马车出门炫耀一番。每一天，每个钟头他都要喝上一瓶新可乐。

pigstd 最近又买了许多箱新可乐——当然，这些可乐只有聪明的人才能喝到。

题目描述

pigstd 现在有 \(n\) 箱可乐，第 \(i\) 箱可乐上标着一个正整数 \(a_{i}\)。

若 pigstd 的聪明值为一个非负整数 \(x\)，对于第 \(i\) 箱可乐，如果 \((a_{i} \oplus x )\le k\)，那么 pigstd 就能喝到这箱可乐。

现在 pigstd 告诉了你 \(k\) 与序列 \(a\)，你可以决定 pigstd 的聪明值 \(x\)，使得他能喝到的可乐的箱数最大。求出这个最大值。

输入格式

第一行两个由空格分隔开的整数 \(n,k\)。

接下来 \(n\) 行，每行一个整数 \(a_i\)，表示第 \(i\) 箱可乐上标的数。

输出格式

一行一个正整数，表示 pigstd 最多能喝到的可乐的箱数。

样例 #1

样例输入 #1

1
2
3
4
3 5
2
3
4

样例输出 #1

1
3

样例 #2

样例输入 #2

1
2
3
4
5
4 625
879
480
671
853

样例输出 #2

1
4

提示

提示

pigstd 的聪明值 \(x\) 可以为 \(0\)。

样例解释

样例 1 解释：容易构造当 \(x = 0\) 时，可以喝到所有可乐。

样例 2 解释：容易构造 \(x = 913\)，可以喝到所有可乐。

样例解释未必是唯一的方法。

数据范围

本题采用捆绑测试。

  • Subtask 1（29 points）：\(1 \le n,k,a_{i} \le 1000\)。

  • Subtask 2（1 points）：\(a_{i} \le k\)。

  • Subtask 3（70 points）：无特殊限制。

对于所有数据，保证 \(1 \le n,k,a_{i} \le 10^6\)。

\(\oplus\) 代表异或，如果您不知道什么是异或，请单击这里。

「EZEC-4」可乐（2种方法：差分+位运算 | 枚举+字典树）-CSDN博客

如果a、b两个值不相同，则异或结果为1。如果a、b两个值相同，异或结果为0。

这篇题解说的一清二楚，烦请大佬借我一用

image-20240225233355522
image-20240225233408120
image-20240225233419017 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include<bits/stdc++.h>
using namespace std;
const int M=1e6+10;
int c[M*2],a[M],n,k,ans,maxn;
int s1[100],s2[100]; 
void f(int b)
{
	memset(s1,0,sizeof(s1));
	memset(s2,0,sizeof(s2));
	int len1=0,len2=0,kk=k;
	while(b)
    {
        s1[++len1]=b%2;
        b/=2;
    }//二进制
	while(kk)
    {
		s2[++len2]=kk%2;
        kk/=2;
    }
    //二进制
	int len=max(len1,len2);
	for (int i=1;i<=len/2;i++)
    {
		swap(s1[i],s1[len-i+1]);
        swap(s2[i],s2[len-i+1]);
    }
    //交换
	int sum=0;
	for (int i=1;i<=len;i++)
		if (s2[i]==0)
			sum=sum*2+s1[i];
    //取相同的
		else
		{
            //可以取相同也可以不同
			int k1=(sum*2+s1[i])*1<<(len-i);
            //看接下来了
             int   k2=(sum*2+1+s1[i])*1<<(len-i);
			c[k1]++,c[k2]--;
			sum=sum*2+(s1[i]^1);
		}
	c[sum]++,c[sum+1]--;
}
int main()
{
	cin>>n>>k;
    maxn=k;
	for (int i=1;i<=n;i++)
	{
		cin>>a[i];
		f(a[i]);
		maxn=max(maxn,a[i]);
	}
	for (int i=1;i<=maxn*2;i++)
		c[i]+=c[i-1];
	for (int i=0;i<=maxn*2;i++)
		ans=max(ans,c[i]);
	cout<<ans;
}

-----------------------------------------------------------------------------

#include<bits/stdc++.h>
using namespace std;
const int N=2e6+5,M=2e4+5,inf=0x3f3f3f3f,mod=1e9+7;
int n,k;
int dp[N];
void f(int x){
	int y=0;
	for(int i=20;~i;i--){
		bool u=k>>i&1,v=x>>i&1;
		if(u&&v) dp[y+(1<<i)]++,dp[y+(1<<i+1)]--; //此时取1会产生贡献.
		else if(u) dp[y]++,dp[y+(1<<i)]--,y+=1<<i;//i位取0
		else if(v) y+=1<<i;//取1保持相等
	}
}
void solve(){
	cin>>n>>k;
	for(int i=1;i<=n;i++){
		int x;cin>>x;
		f(x);
	}
	int ans=dp[0];
	for(int i=1;i<1<<20;i++)
		dp[i]+=dp[i-1],ans=max(ans,dp[i]);
	cout<<ans;
}
int main(){
	solve();
	return 0;
}