补题

涉及内容，二分，贪心，搜索，交互

Bear and Prime 100

题面翻译

这是一道交互题。有一个在闭区间[2,100]里面的整数X，你的任务是判断整数x是质数还是合数。你可以向系统询问一个数是否为该数的约数，询问方式如下： 1.你输出一个在闭区间[2,100]里面的整数 2.系统回答yes或者no(yes表示你输出的数是该数的约数，no表示你输出的数不是该数的约数) 注意：你最多只能提出20次询问！每输出一个询问，你需要使用flush，下面提供一些语言的flush语法： C++语言: fflush(stdout) JAVA语言: System.out.flush() Python语言: stdout.flush() Pascal语言: flush(output)

注：以下内容为译者良心添加以C++语言为例做一个交互示范(假设x=50):

#include<bits/stdc++.h>
using namespace std;
int main()
{
    char s[10],cnt=0;
    cout<<2<<endl;
    fflush(stdout);
    cin>>s;//此时读入为yes，因为2是50的约数
    if(s[0]=='y') cnt++;
    cout<<25<<endl;
    fflush(stdout);
    cin>>s;//此时读入为yes，因为25是50的约数
    if(s[0]=='y') cnt++;
    if(cnt>=2) cout<<"composite"<<endl;
    fflush(stdout);
    return 0;
}

题目描述

This is an interactive problem. In the output section below you will see the information about flushing the output.

Bear Limak thinks of some hidden number — an integer from interval $ [2,100] $ . Your task is to say if the hidden number is prime or composite.

Integer $ x>1 $ is called prime if it has exactly two distinct divisors, $ 1 $ and $ x $ . If integer $ x>1 $ is not prime, it's called composite.

You can ask up to $ 20 $ queries about divisors of the hidden number. In each query you should print an integer from interval $ [2,100] $ . The system will answer "yes" if your integer is a divisor of the hidden number. Otherwise, the answer will be "no".

For example, if the hidden number is $ 14 $ then the system will answer "yes" only if you print $ 2 $ , $ 7 $ or $ 14 $ .

When you are done asking queries, print "prime" or "composite" and terminate your program.

You will get the Wrong Answer verdict if you ask more than $ 20 $ queries, or if you print an integer not from the range $ [2,100] $ . Also, you will get the Wrong Answer verdict if the printed answer isn't correct.

You will get the Idleness Limit Exceeded verdict if you don't print anything (but you should) or if you forget about flushing the output (more info below).

输入格式

After each query you should read one string from the input. It will be "yes" if the printed integer is a divisor of the hidden number, and "no" otherwise.

输出格式

Up to $ 20 $ times you can ask a query — print an integer from interval $ [2,100] $ in one line. You have to both print the end-of-line character and flush the output. After flushing you should read a response from the input.

In any moment you can print the answer "prime" or "composite" (without the quotes). After that, flush the output and terminate your program.

To flush you can use (just after printing an integer and end-of-line):

fflush(stdout) in C++;
System.out.flush() in Java;
stdout.flush() in Python;
flush(output) in Pascal;
See the documentation for other languages.

Hacking. To hack someone, as the input you should print the hidden number — one integer from the interval $ [2,100] $ . Of course, his/her solution won't be able to read the hidden number from the input.

样例 #1

样例输入 #1

1
2
3

yes
no
yes

样例输出 #1

2
80
5
composite

样例 #2

样例输入 #2

no
yes
no
no
no

样例输出 #2

58
59
78
78
2
prime

提示

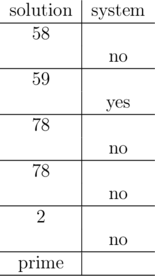
The hidden number in the first query is $ 30 $ . In a table below you can see a better form of the provided example of the communication process.

The hidden number is divisible by both $ 2 $ and $ 5 $ . Thus, it must be composite. Note that it isn't necessary to know the exact value of the hidden number. In this test, the hidden number is $ 30 $ .

$ 59 $ is a divisor of the hidden number. In the interval $ [2,100] $ there is only one number with this divisor. The hidden number must be $ 59 $ , which is prime. Note that the answer is known even after the second query and you could print it then and terminate. Though, it isn't forbidden to ask unnecessary queries (unless you exceed the limit of $ 20 $ queries).

*题意：判断隐藏的数是否素数，该隐藏数范围在2到100，询问最多20次，如果询问数是隐藏数的约数，系统输出yes，否则输出no。*

*思路：//算术基本定理一个合数可以拆分为至少两个质因数的乘积,如果该数是合数，那么他必定有两个及以上质因子组成，最小质因数是2，所以判断50内的素数就行了*

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n)  for(int i=a;i<=n;i++)
const int N=1e6;
using ll=long long;
int a[20]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,4,9,25,49,100};
//算术基本定理一个合数可以拆分为至少两个质因数的乘积
int main()
{
cout<<a[0]<<endl;
fflush(stdout);
string h;
cin>>h;
int cnt=0;
rep(i,1,19)
{
	if(h[0]=='y')
	{
		cnt++;
	}
	cout<<a[i]<<endl;
	fflush(stdout);
	cin>>h;
}
if(cnt>=2)
{
	cout << "composite" << endl;
	fflush(stdout);
	return 0;
}
else
{
	cout << "prime" << endl;
	fflush(stdout);
	return 0;
}

}

数列分段 Section II

题目描述

对于给定的一个长度为 $N$ 的正整数数列 $A_{1\sim N}$，现要将其分成 $M$（$M\leq N$）段，并要求每段连续，且每段和的最大值最小。

关于最大值最小：

例如一数列 $4\ 2\ 4\ 5\ 1$ 要分成 $3$ 段。

将其如下分段：

\[[4\ 2][4\ 5][1]\]

第一段和为 $6$，第 $2$ 段和为 $9$，第 $3$ 段和为 $1$，和最大值为 $9$。

将其如下分段：

\[[4][2\ 4][5\ 1]\]

第一段和为 $4$，第 $2$ 段和为 $6$，第 $3$ 段和为 $6$，和最大值为 $6$。

并且无论如何分段，最大值不会小于 $6$。

所以可以得到要将数列 $4\ 2\ 4\ 5\ 1$ 要分成 $3$ 段，每段和的最大值最小为 $6$。

输入格式

第 $1$ 行包含两个正整数 $N,M$。

第 $2$ 行包含 $N$ 个空格隔开的非负整数 $A_i$，含义如题目所述。

输出格式

一个正整数，即每段和最大值最小为多少。

样例 #1

样例输入 #1

1 2	5 3 4 2 4 5 1

样例输出 #1

提示

对于 $20\%$ 的数据，$N\leq 10$。

对于 $40\%$ 的数据，$N\leq 1000$。

对于 $100\%$ 的数据，$1\leq N\leq 10^5$，$M\leq N$，$A_i < 10^8$，答案不超过 $10^9$。

二分段数即可

水题

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n)  for(int i=a;i<=n;i++)
const int N=1e6+100;
using ll=long long;
int a[N];
int sum;
int n;
int m;
bool check(int x)
{
	int cnt=1;
	int ans=0;
rep(i,1,n)
{
if(ans+a[i]>x)
{
	cnt++;
	ans=a[i];
}
else
{
	ans+=a[i];
}
}
return cnt>m;
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> m;
	int l = 0;
	rep(i, 1, n)
	{
		cin >> a[i];
		sum += a[i];
l=max(l,a[i]);
}
int r=sum;
int mid;
while(l+1<r)
{
	 mid=(l+r)/2;
	if(check(mid))
	{
		l=mid;
	}
	else
	{
		r=mid;
	}
}
if(!check(l))
{
	cout<<l;
}
else
{
	cout<<r;
}
}

Hamburgers

题面翻译

做汉堡包，需要的材料用字符串给出了。

已有的材料数在第二行。（顺序：$B,S,C$）

商店卖的材料的需要的钱数在第三行。（顺序：$B,S,C$）

第四行是你有的钱数。

问最多做多少汉堡。

题目描述

Polycarpus loves hamburgers very much. He especially adores the hamburgers he makes with his own hands. Polycarpus thinks that there are only three decent ingredients to make hamburgers from: a bread, sausage and cheese. He writes down the recipe of his favorite "Le Hamburger de Polycarpus" as a string of letters 'B' (bread), 'S' (sausage) и 'C' (cheese). The ingredients in the recipe go from bottom to top, for example, recipe "ВSCBS" represents the hamburger where the ingredients go from bottom to top as bread, sausage, cheese, bread and sausage again.

Polycarpus has $ n_{b} $ pieces of bread, $ n_{s} $ pieces of sausage and $ n_{c} $ pieces of cheese in the kitchen. Besides, the shop nearby has all three ingredients, the prices are $ p_{b} $ rubles for a piece of bread, $ p_{s} $ for a piece of sausage and $ p_{c} $ for a piece of cheese.

Polycarpus has $ r $ rubles and he is ready to shop on them. What maximum number of hamburgers can he cook? You can assume that Polycarpus cannot break or slice any of the pieces of bread, sausage or cheese. Besides, the shop has an unlimited number of pieces of each ingredient.

输入格式

The first line of the input contains a non-empty string that describes the recipe of "Le Hamburger de Polycarpus". The length of the string doesn't exceed 100, the string contains only letters 'B' (uppercase English B), 'S' (uppercase English S) and 'C' (uppercase English C).

The second line contains three integers $ n_{b} $ , $ n_{s} $ , $ n_{c} $ ( $ 1<=n_{b},n_{s},n_{c}<=100 $ ) — the number of the pieces of bread, sausage and cheese on Polycarpus' kitchen. The third line contains three integers $ p_{b} $ , $ p_{s} $ , $ p_{c} $ ( $ 1<=p_{b},p_{s},p_{c}<=100 $ ) — the price of one piece of bread, sausage and cheese in the shop. Finally, the fourth line contains integer $ r $ ( $ 1<=r<=10^{12} $ ) — the number of rubles Polycarpus has.

Please, do not write the %lld specifier to read or write 64-bit integers in С++. It is preferred to use the cin, cout streams or the %I64d specifier.

输出格式

Print the maximum number of hamburgers Polycarpus can make. If he can't make any hamburger, print 0.

样例 #1

样例输入 #1

BBBSSC
6 4 1
1 2 3
4

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

样例 #3

样例输入 #3

BSC
1 1 1
1 1 3
1000000000000

样例输出 #3

1	200000000001

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+100;
using ll=long long;
#define rep(i,a,n)  for(ll i=a;i<=n;i++)

string s;
ll a,b,c;
ll pa,pb,pc;
ll ca,cb,cc;
ll m;
bool check(ll x)
{
	ll ans=0;
	ll n=0;
	ans+=max((x*a-pa)*ca,n);
	ans += max((x * b - pb) * cb, n);
	ans += max((x * c - pc) * cc, n);
	return m>=ans;
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
string s;
cin>>s;
ll x=s.length()-1;
rep(i,0,x)
{
	if(s[i]=='B')
	{
		a++;
	}
	else if(s[i]=='S')
	{
		b++;
	}
	else
	{
		c++;
	}
}
cin>>pa>>pb>>pc;
cin>>ca>>cb>>cc;
cin>>m;
ll l=0;
ll r=2e12;
ll mid;
while(l+1<r)
{
 mid=(l+r)/2;
if(check(mid))
{
	l=mid+1;
}
else
{
r=mid-1;
}
}
if(check(l+1))
{
	cout<<l+1;
}
else if(check(l))
{
	cout<<l;
}
else
{
	cout<<l-1;
}

}

D - Prime Ring Problem

A ring is compose of n circles as shown in diagram. Put natural number 1, 2, ..., n into each circle separately, and the sum of numbers in two adjacent circles should be a prime.

Note: the number of first circle should always be 1.

Input

n (0 < n < 20).

Output

The output format is shown as sample below. Each row represents a series of circle numbers in the ring beginning from 1 clockwisely and anticlockwisely. The order of numbers must satisfy the above requirements. Print solutions in lexicographical order.

You are to write a program that completes above process.

Print a blank line after each case.

Sample

Inputcopy	Outputcopy
`6 8`	`Case 1: 1 4 3 2 5 6 1 6 5 2 3 4 Case 2: 1 2 3 8 5 6 7 4 1 2 5 8 3 4 7 6 1 4 7 6 5 8 3 2 1 6 7 4 3 8 5 2`

题意：

输入正整数 n，把整数 1,2,… 组成一个环，使得相邻两个整数之和均为素数。输出时，从整数 11 开始逆时针排列。同一个环恰好输出一次。n*≤16，保证一定有解。

多组数据，读入到 EOF 结束。

第 i* 组数据输出前加上一行 Case i:

相邻两组数据中间加上一个空行。

一般的搜索，要加个素数进行剪枝

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+100;
using ll=long long;
#define rep(i,a,n)  for(ll i=a;i<=n;i++)
bool vis[20];//记录
int a[20];//存放
int n;
int cnt=1;
bool isprime(int x)
{
    if(x<2)return false;
    if(x==2)return true;
    for(int i=2;i<=sqrt(x);i++)
	{
	if(x%i==0)  return false;
    }
    return true;
}
void dfs(int step)
{
	if(isprime(a[1]+a[n])&&step==n+1)
	{
		rep(i,1,n)
		{
		cout<<a[i]<<' ';	
		}
		cout<<'\n';
		return ;
	}
	rep(i,2,n)
	{
		if(!vis[i]&&isprime(i+a[step-1]))
	{
		vis[i]=1;
		a[step]=i;
		dfs(step+1);
		vis[i]=0;
	}
	}
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
while(cin>>n)
{
if(cnt>1)cout<<'\n';
	cout<<"Case "<<cnt<<":"<<'\n';
	cnt++;
	a[1]=1;
	vis[1]=1;
	dfs(2);
	memset(vis,0,sizeof(vis));
}
}

Cinema

题面翻译

莫斯科在举办一场重要的有$n$ 个不同国家的珂学家参与的国际会议，每个珂学家都只会一种语言。为了方便起见，我们规定一种语言用$1$ 到$10^9$ 的数来描述。在会议之后的晚上，珂学家们决定去看电影。他们去的电影院有$m$ 场电影，每场有两个不同的数字，分别代表配音的语言和字幕的语言。如果一个珂学家能听懂配音，他会非常愉悦；如果能看懂字幕，他会比较满意。如果既看不懂也听不懂，他会很生气。珂学家们决定去看同一场电影，你必须帮助他们选择一场电影，让愉悦的人最多的前提下，比较满意的人最多。输入格式：第一行一个整数$n(1 \leq n \leq 200000)$ 表示珂学家个数。第二行$n$ 个整数$a_1, a_2, ..., a_n(1 \leq a_i \leq 10^9)$ 表示珂学家们会的语言。第三行一个整数$1 \leq m \leq 200000$ 表示电影的场数。第四行$m$ 个整数$b_1, b_2, ..., b_n(1 \leq b_j \leq 10^9)$ 表示电影的配音用的语言。第五行$m$ 个整数$c_1, c_2, ..., c_n(1 \leq c_j \leq 10^9)$ 表示电影的字幕用的语言。输出格式：一个整数表示安排哪一场电影。如果有多种情况，选择比较满意的方案输出。

题目描述

Moscow is hosting a major international conference, which is attended by $ n $ scientists from different countries. Each of the scientists knows exactly one language. For convenience, we enumerate all languages of the world with integers from $ 1 $ to $ 10^{9} $ .

In the evening after the conference, all $ n $ scientists decided to go to the cinema. There are $ m $ movies in the cinema they came to. Each of the movies is characterized by two distinct numbers — the index of audio language and the index of subtitles language. The scientist, who came to the movie, will be very pleased if he knows the audio language of the movie, will be almost satisfied if he knows the language of subtitles and will be not satisfied if he does not know neither one nor the other (note that the audio language and the subtitles language for each movie are always different).

Scientists decided to go together to the same movie. You have to help them choose the movie, such that the number of very pleased scientists is maximum possible. If there are several such movies, select among them one that will maximize the number of almost satisfied scientists.

输入格式

The first line of the input contains a positive integer $ n $ ( $ 1<=n<=200000 $ ) — the number of scientists.

The second line contains $ n $ positive integers $ a_{1},a_{2},...,a_{n} $ ( $ 1<=a_{i}<=10^{9} $ ), where $ a_{i} $ is the index of a language, which the $ i $ -th scientist knows.

The third line contains a positive integer $ m $ ( $ 1<=m<=200000 $ ) — the number of movies in the cinema.

The fourth line contains $ m $ positive integers $ b_{1},b_{2},...,b_{m} $ ( $ 1<=b_{j}<=10^{9} $ ), where $ b_{j} $ is the index of the audio language of the $ j $ -th movie.

The fifth line contains $ m $ positive integers $ c_{1},c_{2},...,c_{m} $ ( $ 1<=c_{j}<=10^{9} $ ), where $ c_{j} $ is the index of subtitles language of the $ j $ -th movie.

It is guaranteed that audio languages and subtitles language are different for each movie, that is $ b_{j}≠c_{j} $ .

输出格式

Print the single integer — the index of a movie to which scientists should go. After viewing this movie the number of very pleased scientists should be maximum possible. If in the cinema there are several such movies, you need to choose among them one, after viewing which there will be the maximum possible number of almost satisfied scientists.

If there are several possible answers print any of them.

样例 #1

样例输入 #1

样例输出 #1

样例 #2

样例输入 #2

6
6 3 1 1 3 7
5
1 2 3 4 5
2 3 4 5 1

样例输出 #2

提示

In the first sample, scientists must go to the movie with the index $ 2 $ , as in such case the $ 1 $ -th and the $ 3 $ -rd scientists will be very pleased and the $ 2 $ -nd scientist will be almost satisfied.

In the second test case scientists can go either to the movie with the index $ 1 $ or the index $ 3 $ . After viewing any of these movies exactly two scientists will be very pleased and all the others will be not satisfied.

将后面两次输入存在一个数组里面，然后用a数组来进行映射，计算了总共出现了几次，然后再进行查询，看哪部电影最符合

#include<iostream>
#include<algorithm>
using namespace std;
using ll = long long;
const int N = 1e6 + 10;
ll a[N], b[N], c[N], d[N];
ll cnt[N];
int tot, m, n;
void disc() {
	sort(d + 1, d + tot + 1);
	tot = unique(d + 1, d + tot + 1) - (d + 1);
}
int find(int x) {
	return lower_bound(d + 1, d + 1 + tot, x) - (d + 1);
}
void solve() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
		d[++tot] = a[i];
	}
	cin >> m;
	for (int i = 1; i <= m; i++) {
		cin >> b[i];
		d[++tot] = b[i];
	}
	for (int i = 1; i <= m; i++) {
		cin >> c[i];
		d[++tot] = c[i];
	}
	disc();
	for (int i = 1; i <= n; i++) {
		cnt[find(a[i])]++;
	}
	int ans = 1;
	pair<int, int> P = { 0,0 };
	for (int i = 1; i <= m; i++) {
		int x = cnt[find(b[i])], y = cnt[find(c[i])];
		if (make_pair(x, y) > P) {
			ans = i;
			P = { x,y };
		}
	}
	cout << ans << "\n";
}
int main() 
{
	solve();
	return 0;
}

F - Cup

The WHU ACM Team has a big cup, with which every member drinks water. Now, we know the volume of the water in the cup, can you tell us it height?

The radius of the cup's top and bottom circle is known, the cup's height is also known.

Input

The input consists of several test cases. The first line of input contains an integer T, indicating the num of test cases. Each test case is on a single line, and it consists of four floating point numbers: r, R, H, V, representing the bottom radius, the top radius, the height and the volume of the hot water.

Technical Specification

T ≤ 20.
1 ≤ r, R, H ≤ 100; 0 ≤ V ≤ 1000,000,000.
r ≤ R.
r, R, H, V are separated by ONE whitespace.
There is NO empty line between two neighboring cases.

Output

For each test case, output the height of hot water on a single line. Please round it to six fractional digits.

Sample

Inputcopy	Outputcopy
`1 100 100 100 3141562`	`99.999024`

二分高度即可

需要一些数学知识

不过不那么深

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+100;
using ll=long long;
#define rep(i,a,n)  for(ll i=a;i<=n;i++)
const double pi=3.141592654;
int main()
{
//	ios::sync_with_stdio(0);
	//cin.tie(0);
	//cout.tie(0);
int t;
cin>>t;
while(t--)
{
double r,R,v,H;
cin>>r>>R>>H>>v;
//double V=pi/3*H*(r*r+R*R+R*r);
double L=0;
double _R=H;
double MId;
//double ratio=V/v;
while(_R-L>1e-9)
{
	MId=(L+_R)/2;
double Rr=MId*(R-r)/H+r;
	double _v=pi/3*MId*(r*r+Rr*Rr+Rr*r);
if(abs(_v-v)<=1e-9)
{
break;
}
	else if(_v<v)
	{
		L=MId;	
	}
	else
	{
	_R=MId;
	}
}
printf("%.6f",MId);	
}
return 0;
}

G - Bins and Balls

Bins and Balls Input file: standard input Output file: standard output Time limit: 2 seconds Memory limit: 512 mebibytes You have several balls of n different colors. For each color i from 1 to n, there are exactly xi balls of this color. You are playing a game which is a sequence of actions. In one action, you can take exactly k balls of pairwise distinct colors and throw them away. What is the maximum number of actions that you can make? Input The first line contains two integers n and k: the number of colors and the number of balls that you throw away in each action (1 ≤ k ≤ n ≤ 2 · 105 ). The second line contains n space-separated integers xi : the number of balls of the i-th color (1 ≤ xi ≤ 109 ). Output Print a single line with one integer: the maximum possible number of actions you can make.

Examples standard input standard output 4 3 5 8 9 4

10 5 1 2 3 4 5 6 239 239 239 239

直接进行二分即可

每次都把首尾往里面加，这样就保证了最优

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for(ll i=a;i<=n;i++)
#define frep(i,a,n) for(ll i=a;i>=n;i--)
const int N=1e6;
using ll=long long;
int n,m;
ll a[N];
ll b[N];
bool check(ll mid)
{
	rep(i,1,n)
	{
		b[i]=a[i];
	}
	ll i=1;
	frep(j,n,n-m+1)
	{
		while(b[j]<mid&&i<n-m+1)
		{
				if(b[i]+b[j]<mid)
		{
			b[j]+=b[i];
			i++;
		}
		else
		{
			b[i]-=mid-b[j];
			b[j]=mid;
		}
		}
	
	}
	frep(j,n,n-m+1)
	{
		if(b[j]<mid)
		{
			return 0;
		}
	}
		return 1;
}
int main()
{
cin>>n>>m;
rep(i,1,n)
{
	cin>>a[i];
}
sort(a+1,a+1+n);
ll l=1;
ll r=1e18;
while(l+1<r)
{
	ll mid=(l+r)/2;
	if(check(mid))
	{
		l=mid+1;
	}
	else
	{
		r=mid-1;
	}
}

if(check(l+1))
{
	cout<<l+1;
}
else if(check(l))
{
	cout<<l;
}
else
{
	cout<<l-1;
}


}

[COCI2012-2013#1] LJUBOMORA

题目描述

一家弹珠厂向一所幼儿园捐赠了一些弹珠，弹珠一共有 $M$ 种颜色，每颗弹珠都有一种颜色。老师需要把所有的弹珠分给 $N$ 个孩子。每个孩子得到的所有弹珠都必须是相同的颜色，而且可以有一些孩子一颗弹珠也没得到。

我们把嫉妒值定义为分给一个孩子最多的弹珠数量。请你帮助老师分弹珠，使得嫉妒值最小。

例如，如果有 $4$ 个红色的弹珠（$\texttt{RRRR}$）和 $7$ 个蓝色的弹珠（$\texttt{BBBBBBB}$），要分给 $5$ 个孩子，那么我们可以这样划分：$\texttt{RR}$，$\texttt{RR}$，$\texttt{BB}$，$\texttt{BB}$，$\texttt{BBB}$。这样分的嫉妒值为 $3$，是最小的。

输入格式

输入共 $M+1$ 行。

第一行包含两个正整数 $N,M$，分别表示孩子数和弹珠的颜色总数。

接下来 $M$ 行的第 $i$ 行包含一个正整数 $x$（$x \in [1,10^9]$），表示有 $x$ 个颜色为 $i$ 的弹珠。

输出格式

输出一行一个整数，表示最小的嫉妒值。

样例 #1

样例输入 #1

1
2
3

5 2
7
4

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

提示

【数据范围】

对于 $100\%$ 的数据，保证 $1 \le M \le 3 \times 10^5$，$1 \le N \le 10^9$，$M \le N$。

【说明】

本题分值按 COCI 原题设置，满分 $120$。

题目译自 COCI2012-2013 CONTEST #1 T4 LJUBOMORA。

也是非常简单的二分

只需要枚举最大值

然后贪心的进行除法

注意，如果无法整除的话

要sum++

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+100;
using ll=long long;
#define rep(i,a,n)  for(ll i=a;i<=n;i++)
ll ans;
ll n,m;
ll a[N];
bool check(ll x)
{
	ll sum=0;
	rep(i,1,m)
	{
		sum+=a[i]/x;
		if(a[i]%x)
		{
			sum++;
		}
	}
	return sum<=n;
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
cin>>n>>m;
rep(i,1,m)
{
	cin>>a[i];
	ans+=a[i];
}
ll l=0;
ll r=ans;
while(l+1<r)
{
	ll mid=(l+r)/2;
	if(check(mid))
	{
r=mid-1;	
	}
	else
	{
	l=mid+1;
	}
}
 if(check(l-1))
{
	cout<<l-1;
}
else if(check(l))
{
	cout<<l;
}
else
{
	cout<<l+1;
}


return 0;
}

Black and White Stripe

题面翻译

题意翻译

给出 $n$ 和 $m$，还有一个长度为 $n$ 且只包含 B 和 W 的字符串。

问在字符串中找出一个长度为 $m$ 且只包含 B 的子串最少需要修改多少个 W。

多组测试。

题目描述

You have a stripe of checkered paper of length $ n $ . Each cell is either white or black.

What is the minimum number of cells that must be recolored from white to black in order to have a segment of $ k $ consecutive black cells on the stripe?

If the input data is such that a segment of $ k $ consecutive black cells already exists, then print 0.

输入格式

The first line contains an integer $ t $ ( $ 1 t ^4 $ ) — the number of test cases.

Next, descriptions of $ t $ test cases follow.

The first line of the input contains two integers $ n $ and $ k $ ( $ 1 k n ^5 $ ). The second line consists of the letters 'W' (white) and 'B' (black). The line length is $ n $ .

It is guaranteed that the sum of values $ n $ does not exceed $ 2^5 $ .

输出格式

For each of $ t $ test cases print an integer — the minimum number of cells that need to be repainted from white to black in order to have a segment of $ k $ consecutive black cells.

样例 #1

样例输入 #1

4
5 3
BBWBW
5 5
BBWBW
5 1
BBWBW
1 1
W

样例输出 #1

提示

In the first test case, $ s $ ="BBWBW" and $ k=3 $ . It is enough to recolor $ s_3 $ and get $ s $ ="BBBBW". This string contains a segment of length $ k=3 $ consisting of the letters 'B'.

In the second test case of the example $ s $ ="BBWBW" and $ k=5 $ . It is enough to recolor $ s_3 $ and $ s_5 $ and get $ s $ ="BBBBB". This string contains a segment of length $ k=5 $ consisting of the letters 'B'.

In the third test case of the example $ s $ ="BBWBW" and $ k=1 $ . The string $ s $ already contains a segment of length $ k=1 $ consisting of the letters 'B'.

要把黑的变成相应的白的，只需要进行前缀和枚举一下，黑最多有多少个

然后在那段区间里面去减就可以了

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+100;
using ll=long long;
#define rep(i,a,n)  for(ll i=a;i<=n;i++)
int a[N];
int sum[N];
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
int t;
cin>>t;
while(t--)
{
	int ans=0;
	int n,m;
	cin>>n>>m;
	string s;
	cin>>s;
	rep(i,0,n-1)
	{
		if(s[i]=='B')
		{
			a[i+1]=1;
		}
		else
		{
			a[i+1]=0;
		}
		sum[i+1]=sum[i]+a[i+1];
	}
	rep(i,1,n-m+1)
	{
		ans=max(ans,sum[i+m-1]-sum[i-1]);
		a[i]=0;
	}
	cout<<m-ans<<'\n';
}
return 0;
}

Balanced Stone Heaps

题面翻译

你有 $n$ 堆石子，其中第 $i$ 堆里面有 $h_i$ 粒石子。你需要从第 $3$ 堆石子开始从前往后进行操作。设当前为第 $i$ 堆石子，你可以选择一个在 $[0,\frac {h_i}3]$ 的整数 $d$，从第 $i$ 堆石子中取出 $3d$ 粒石子，然后往第 $i-1$ 堆石子里放入 $d$ 粒石子，往第 $i-2$ 堆石子里放入 $2d$ 粒石子。

你需要通过合理设计操作方案，使得数量最少的一堆石子的数量最大。请求出这个最大值。

数据范围：

$t$ 组数据，$1\leqslant t\leqslant 2\times 10^5$。
$3\leqslant n,\sum n\leqslant 2\times 10^5$。
$1\leqslant h_i\leqslant 10^9$。

Translated by Eason_AC
2021.12.29

题目描述

There are $ n $ heaps of stone. The $ i $ -th heap has $ h_i $ stones. You want to change the number of stones in the heap by performing the following process once:

You go through the heaps from the $ 3 $ -rd heap to the $ n $ -th heap, in this order.
Let $ i $ be the number of the current heap.
You can choose a number $ d $ ( $ 0 d h_i $ ), move $ d $ stones from the $ i $ -th heap to the $ (i - 1) $ -th heap, and $ 2 d $ stones from the $ i $ -th heap to the $ (i - 2) $ -th heap.
So after that $ h_i $ is decreased by $ 3 d $ , $ h_{i - 1} $ is increased by $ d $ , and $ h_{i - 2} $ is increased by $ 2 d $ .
You can choose different or same $ d $ for different operations. Some heaps may become empty, but they still count as heaps.

What is the maximum number of stones in the smallest heap after the process?

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 t ^5 $ ). Description of the test cases follows.

The first line of each test case contains a single integer $ n $ ( $ 3 n ^5 $ ).

The second lines of each test case contains $ n $ integers $ h_1, h_2, h_3, , h_n $ ( $ 1 h_i ^9 $ ).

It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 ^5 $ .

输出格式

For each test case, print the maximum number of stones that the smallest heap can contain.

样例 #1

样例输入 #1

4
4
1 2 10 100
4
100 100 100 1
5
5 1 1 1 8
6
1 2 3 4 5 6

样例输出 #1

提示

In the first test case, the initial heap sizes are $ [1, 2, 10, 100] $ . We can move the stones as follows.

move $ 3 $ stones and $ 6 $ from the $ 3 $ -rd heap to the $ 2 $ -nd and $ 1 $ heap respectively. The heap sizes will be $ [7, 5, 1, 100] $ ;
move $ 6 $ stones and $ 12 $ stones from the last heap to the $ 3 $ -rd and $ 2 $ -nd heap respectively. The heap sizes will be $ [7, 17, 7, 82] $ .

In the second test case, the last heap is $ 1 $ , and we can not increase its size.

In the third test case, it is better not to move any stones.

In the last test case, the final achievable configuration of the heaps can be $ [3, 5, 3, 4, 3, 3] $ .

从后往前二分即可达成目标

最后比较a[1]和a[2]即可。

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+100;
using ll=long long;
#define rep(i,a,n)  for(ll i=a;i<=n;i++)
#define frep(i,a,n) for(ll i=a;i>=n;i--)
int a[N];
int b[N];
int n;
bool check(int x)
{
	
	frep(i,n,3)
	{
		if(a[i]<x)
		{
			return 0;
		}
		int d=min(b[i],a[i]-x)/3;
		a[i-1]+=d;
		a[i-2]+=2*d;
		a[i]-=3*d;
	}
	if(a[1]>=x&&a[2]>=x)
	{
		return 1;
	}
	return  0;
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
int t;
cin>>t;
while(t--)
{
int ans;
	cin>>n;
	rep(i,1,n)
	{
		cin>>a[i];
		b[i]=a[i];
	}
	int l=1;
	int r=1e9;
	int mid;
	while(l<=r)
	{
	 mid=(l+r)/2;
	if(check(mid))
	{
		l=mid+1;
		ans=mid;
	}	
	else
	{
		r=mid-1;
	}
	rep(i,1,n)
{
	a[i]=b[i];
}
	}

	cout<<ans<<'\n';

}



}

K - The Enchanted Forest

贪心一点想，直接向前走肯定比回头好，除非到了尽头

那么本题结束。

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
using namespace std;
const int N=1e6;
ll a[N],sum[N];
int main()
{
	ll t,n,k,i,ans;
    cin>>t;
	while(t--)
	{
	cin>>n>>k;
		for(i=1;i<=n;i++)
		{
			cin>>a[i];
			sum[i]=sum[i-1]+a[i];
		}
		if(n<k)
		{
			cout<<sum[n]+n*(k*2-n-1)/2<<'\n';
			continue;
		}
		ans=0;
		for(i=k;i<=n;i++)
		ans=max(ans,sum[i]-sum[i-k]+(k-1)*k/2);
		cout<<ans<<'\n';
	}
	return 0;
}

L - Occupy the Cities

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+100;
using ll=long long;
#define rep(i,a,n)  for(ll i=a;i<=n;i++)
#define frep(i,a,n) for(ll i=a;i>=n;i--)
int n;
string s;
bool check(int x){
int len=0;
rep(i,0,n-1)
{
	if(s[i]=='0')len++;
	else{
			if(len<x)len=-x;
			else if(len==x)len=-max(x-1,0);
			else return 0;
		}
	}
	if(len>0)return 0;
	return 1;
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
int t;
cin>>t;
while(t--)
{
	cin>>n;
	cin>>s;	
int l=0,r=n;
	while(l<r){
		int mid=l+r>>1;
		if(check(mid))
		{
		r=mid;
	}
		else 
		{
		l=mid+1;
	}
	}
	cout<<l<<'\n';

}
}