【模板】单调栈

题目背景

模板题，无背景。

2019.12.12 更新数据，放宽时限，现在不再卡常了。

题目描述

给出项数为 \(n\) 的整数数列 \(a_{1 \dots n}\)。

定义函数 \(f(i)\) 代表数列中第 \(i\) 个元素之后第一个大于 \(a_i\) 的元素的下标，即 \(f(i)=\min_{i<j\leq n, a_j > a_i} \{j\}\)。若不存在，则 \(f(i)=0\)。

试求出 \(f(1\dots n)\)。

输入格式

第一行一个正整数 \(n\)。

第二行 \(n\) 个正整数 \(a_{1\dots n}\)。

输出格式

一行 \(n\) 个整数表示 \(f(1), f(2), \dots, f(n)\) 的值。

样例 #1

样例输入 #1

1
2
5
1 4 2 3 5

样例输出 #1

1
2 5 4 5 0

提示

【数据规模与约定】

对于 \(30\%\) 的数据，\(n\leq 100\)；

对于 \(60\%\) 的数据，\(n\leq 5 \times 10^3\) ；

对于 \(100\%\) 的数据，\(1 \le n\leq 3\times 10^6\)，\(1\leq a_i\leq 10^9\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for(int i=a;i<=n;i++)
int n;
const int N=5e6;
int a[N];
int stk[N];
int ans[N];
int main()
{
cin>>n;
int top=0;
rep(i,1,n)
{
	cin>>a[i];
while(top && !(a[stk[top]]>=a[i]))	
ans[stk[top--]]=i;
	stk[++top]=i;
}
//构造一个单调递减栈
rep(i,1,n)
{
	cout<<ans[i]<<' ';
}


滑动窗口 /【模板】单调队列

题目描述

有一个长为 \(n\) 的序列 \(a\)，以及一个大小为 \(k\) 的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如，对于序列 \([1,3,-1,-3,5,3,6,7]\) 以及 \(k = 3\)，有如下过程：

\[\def\arraystretch{1.2} \begin{array}{|c|c|c|}\hline \textsf{窗口位置} & \textsf{最小值} & \textsf{最大值} \\ \hline \verb![1 3 -1] -3 5 3 6 7 ! & -1 & 3 \\ \hline \verb! 1 [3 -1 -3] 5 3 6 7 ! & -3 & 3 \\ \hline \verb! 1 3 [-1 -3 5] 3 6 7 ! & -3 & 5 \\ \hline \verb! 1 3 -1 [-3 5 3] 6 7 ! & -3 & 5 \\ \hline \verb! 1 3 -1 -3 [5 3 6] 7 ! & 3 & 6 \\ \hline \verb! 1 3 -1 -3 5 [3 6 7]! & 3 & 7 \\ \hline \end{array} \]

输入格式

输入一共有两行，第一行有两个正整数 \(n,k\)。 第二行 \(n\) 个整数，表示序列 \(a\)

输出格式

输出共两行，第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值

样例 #1

样例输入 #1

1
2
8 3
1 3 -1 -3 5 3 6 7

样例输出 #1

1
2
-1 -3 -3 -3 3 3
3 3 5 5 6 7

提示

【数据范围】
对于 \(50\%\) 的数据，\(1 \le n \le 10^5\)；
对于 \(100\%\) 的数据，\(1\le k \le n \le 10^6\)，\(a_i \in [-2^{31},2^{31})\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define frep(i, a, n) for (int i = a; i >= n; i--)
using ll = long long;
const int N = 1e7;
int a[N];
int q[N];
int q2[N];
int main()
{
int n,m;
cin>>n>>m;
rep(i,1,n)
{
    cin>>a[i];
}
int h=1,t=0;
rep(i,1,n)
{

while (h <= t && q[h] + m <= i)
{
    h++;
}
while (h <= t && a[i]<a[q[t]])
{
    t--;
}
q[++t] = i;
if(i>=m)
{
    cout<<a[q[h]]<<' ';
}
}
cout<<'\n';
 h = 1, t = 0;
rep(i, 1, n)
{

    while (h <= t && q2[h] + m <= i)
    {
        h++;
    }
    while (h <= t && a[i] > a[q2[t]])
    {
        t--;
    }
    q2[++t] = i;
    if (i >= m)
    {
        cout << a[q2[h]] << ' ';
    }
}
}

约瑟夫问题

题目描述

\(n\) 个人围成一圈，从第一个人开始报数,数到 \(m\) 的人出列，再由下一个人重新从 \(1\) 开始报数，数到 \(m\) 的人再出圈，依次类推，直到所有的人都出圈，请输出依次出圈人的编号。

注意：本题和《深入浅出-基础篇》上例题的表述稍有不同。书上表述是给出淘汰 \(n-1\) 名小朋友，而该题是全部出圈。

输入格式

输入两个整数 \(n,m\)。

输出格式

输出一行 \(n\) 个整数，按顺序输出每个出圈人的编号。

样例 #1

样例输入 #1

1
10 3

样例输出 #1

1
3 6 9 2 7 1 8 5 10 4

提示

\(1 \le m, n \le 100\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
queue < int>q;
int n, k;
int main()
{
	cin >> n >> k;
	for (int i =1; i <=n ; i++)
	{
		q.push(i);
	}
	while (q.size()!=0)
	{
		for (int i = 1; i < k; i++)
		{
			q.push(q.front());
			q.pop();

		}
		cout << q.front()<<" ";
		q.pop();
//真正的pop

	}



}

括号序列

题目描述

定义如下规则：

  1. 空串是「平衡括号序列」
  2. 若字符串 \(S\) 是「平衡括号序列」，那么 \(\texttt{[}S\texttt]\) 和 \(\texttt{(}S\texttt)\) 也都是「平衡括号序列」
  3. 若字符串 \(A\) 和 \(B\) 都是「平衡括号序列」，那么 \(AB\)（两字符串拼接起来）也是「平衡括号序列」。

例如，下面的字符串都是平衡括号序列：

  • ()，[]，(())，([])，()[]，()[()]

而以下几个则不是：

  • (，[，]，)(，())，([()

现在，给定一个仅由 (，)，[，]构成的字符串 \(s\)，请你按照如下的方式给字符串中每个字符配对：

  1. 从左到右扫描整个字符串。
  2. 对于当前的字符，如果它是一个右括号，考察它与它左侧离它最近的未匹配的的左括号。如果该括号与之对应（即小括号匹配小括号，中括号匹配中括号），则将二者配对。如果左侧未匹配的左括号不存在或与之不对应，则其配对失败。

配对结束后，对于 \(s\) 中全部未配对的括号，请你在其旁边添加一个字符，使得该括号和新加的括号匹配。

输入格式

输入只有一行一个字符串，表示 \(s\)。

输出格式

输出一行一个字符串表示你的答案。

样例 #1

样例输入 #1

1
([()

样例输出 #1

1
()[]()

样例 #2

样例输入 #2

1
([)

样例输出 #2

1
()[]()

提示

数据规模与约定

对于全部的测试点，保证 \(s\) 的长度不超过 \(100\)，且只含 (，)，[，] 四种字符。

见注释

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include<iostream>
#include<algorithm>
#include<stack>
#include<queue>
#include<string>
using namespace std;
struct point
{
	char c;
	int pos;
};
bool mark[105];
int main()
{
	string s;
	stack<point>p_s;
		cin >>s;
		for (int i = 0; i < s.size(); i++)
		{
			if (s[i] == '(' || s[i] == '[')
			{
				p_s.push({ s[i], i });
				continue;
			}
			if (p_s.empty())
			{
				continue;
			}
			point p = p_s.top();
			if (s[i] == ')' && p.c == '(' || s[i] == ']' && p.c == '[')
                //相邻的记录一下，这样就可以直接输出了
			{
				mark[i] = 1;
				mark[p.pos] = 1;
				p_s.pop();

			}
			else
			{
				continue;
			}
	}
		for (int i = 0; i < s.size(); i++)
		{
			if (mark[i]==1)
			{
				cout << s[i];
			}
			else if (s[i]=='('||s[i]==')')
				{
					cout << "()";
				}
			else
			{
				cout << "[]";
			}
		}
}

[HAOI2007] 理想的正方形

题目描述

有一个 \(a \times b\) 的整数组成的矩阵，现请你从中找出一个 \(n \times n\) 的正方形区域，使得该区域所有数中的最大值和最小值的差最小。

输入格式

第一行为 \(3\) 个整数，分别表示 \(a,b,n\) 的值。

第二行至第 \(a+1\) 行每行为 \(b\) 个非负整数，表示矩阵中相应位置上的数。每行相邻两数之间用一空格分隔。

输出格式

仅一个整数，为 \(a \times b\) 矩阵中所有“ \(n \times n\) 正方形区域中的最大整数和最小整数的差值”的最小值。

样例 #1

样例输入 #1

1
2
3
4
5
6
5 4 2
1 2 5 6
0 17 16 0
16 17 2 1
2 10 2 1
1 2 2 2

样例输出 #1

1
1

提示

问题规模。

矩阵中的所有数都不超过 \(1,000,000,000\)。

\(20\%\) 的数据 \(2 \le a,b \le 100,n \le a,n \le b,n \le 10\)。

\(100\%\) 的数据 \(2 \le a,b \le 1000,n \le a,n \le b,n \le 100\)。

..用单调队列分别维护行与列。

最后就可以压缩成一个格子了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int m[N][N];
int q[N];
int rowmin[N][N];
int rowmax[N][N];
int colmin[N][N];
int colmax[N][N];
int a,b,n;
int ans=1000000000;
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define frep(i, a, n) for (int i = a; i >= n; i--)
int main()
{
cin>>a>>b>>n;
rep(i,1,a)
{
    rep(j,1,b)
    {
        cin>>m[i][j];
    }
}
rep(row,1,a)
{
    int  h=0;
     int t=0;
rep(i,1,b)
{
    while(h<t&&q[h]+n<=i)
    {
        h++;
    }
    while(h<t&&m[row][q[t-1]]<m[row][i])
    {
        t--;
    }
    q[t]=i;
    t++;
if(i>=n)
{
    rowmax[row][i-n+1]=m[row][q[h]];
}
}
h=0,t=0;
rep(i, 1, b)
{
    while (h < t && q[h]+n <=i )
    {
        h++;
    }
    while (h <t && m[row][q[t - 1]] > m[row][i])
    {
        t--;
    }
    q[t] = i;
    t++;
    if (i >= n)
    {
        rowmin[row][i - n + 1] = m[row][q[h]];
    }
}
}
rep(col,1,b-n+1)
{
  int   h=0;
    int t=0;
    rep(i,1,a)
    {
        while(h<t&&q[h]+n<=i)
        {
            h++;
        }
        while(h<t&&rowmax[q[t-1]][col]<rowmax[i][col])
        {
            t--;
        }
        q[t]=i;
        t++;
        if(i>=n)
        {
            colmax[i-n+1][col]=rowmax[q[h]][col];
        }
    }
     h=0;
    t=0;
    rep(i,1,a)
    {
        while(h<t&&q[h]+n<=i)
        {
            h++;
        }
        while(h<t&&rowmin[q[t-1]][col]>rowmin[i][col])
        {
            t--;
        }
        q[t]=i;
        t++;
        if(i>=n)
        {
            colmin[i-n+1][col]=rowmin[q[h]][col];
        }
    }
   
}

rep(i,1,a-n+1)
{
    rep(j,1,b-n+1)
    {
        if(colmax[i][j]-colmin[i][j]<ans)
        {
            ans=colmax[i][j]-colmin[i][j];
        }
    }
}
cout<<ans;



}





最小函数值

题目描述

有 \(n\) 个函数，分别为 \(F_1,F_2,\dots,F_n\)。定义 \(F_i(x)=A_ix^2+B_ix+C_i(x\in\mathbb N*)\)。给定这些 \(A_i\)、\(B_i\) 和 \(C_i\)，请求出所有函数的所有函数值中最小的 \(m\) 个（如有重复的要输出多个）。

输入格式

第一行输入两个正整数 \(n\) 和 \(m\)。

以下 \(n\) 行每行三个正整数，其中第 \(i\) 行的三个数分别为 \(A_i\)、\(B_i\) 和 \(C_i\)。

输出格式

输出将这 \(n\) 个函数所有可以生成的函数值排序后的前 \(m\) 个元素。这 \(m\) 个数应该输出到一行，用空格隔开。

样例 #1

样例输入 #1

1
2
3
4
3 10
4 5 3
3 4 5
1 7 1

样例输出 #1

1
9 12 12 19 25 29 31 44 45 54

提示

数据规模与约定

对于全部的测试点，保证 \(1 \leq n,m\le10000\)，\(1 \leq A_i\le10,B_i\le100,C_i\le10^4\)。

保证了都是正数，那么可以先放1，然后再放最小的1的2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for(int i=a;i<=n;i++)
const int N=5e6;
using ll=long long;
ll n,m;
struct node
{
	ll val;
	ll x;
	ll from;
};
bool operator <(node a,node b)
{
	return a.val>b.val;
}
priority_queue<node>q;
struct hanshu
{
	int a,b,c;
}b[N];
ll jisuan(ll i,ll x)
{
return b[i].a*x*x+b[i].b*x+b[i].c;
}
int main()
{
	cin>>n>>m;
	rep(i,1,n)
	{
		cin>>b[i].a>>b[i].b>>b[i].c;
		q.push((node){jisuan(i,1),1,i});
	}

rep(i,1,m)
{
	node h=q.top();
	cout<<h.val<<' '; 
	q.pop();
	q.push((node){jisuan(h.from,h.x+1),h.x+1,h.from});	
}	
	
	
}

亲戚

题目背景

若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。

题目描述

规定：\(x\) 和 \(y\) 是亲戚，\(y\) 和 \(z\) 是亲戚，那么 \(x\) 和 \(z\) 也是亲戚。如果 \(x\)，\(y\) 是亲戚，那么 \(x\) 的亲戚都是 \(y\) 的亲戚，\(y\) 的亲戚也都是 \(x\) 的亲戚。

输入格式

第一行：三个整数 \(n,m,p\)，（\(n,m,p \le 5000\)），分别表示有 \(n\) 个人，\(m\) 个亲戚关系，询问 \(p\) 对亲戚关系。

以下 \(m\) 行：每行两个数 \(M_i\)，\(M_j\)，\(1 \le M_i,~M_j\le n\)，表示 \(M_i\) 和 \(M_j\) 具有亲戚关系。

接下来 \(p\) 行：每行两个数 \(P_i,P_j\)，询问 \(P_i\) 和 \(P_j\) 是否具有亲戚关系。

输出格式

\(p\) 行，每行一个 Yes 或 No。表示第 \(i\) 个询问的答案为“具有”或“不具有”亲戚关系。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6

样例输出 #1

1
2
3
Yes
Yes
No
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include<iostream>
using namespace std;
int f[1000000];

int find(int x)
{
	if (x==f[x])
	{
		return x;
	}

	return f[x]=find(f[x]);

}


int main()
{
	int n, m, p,x,y;
	cin >> n >> m >> p;

	for (int i = 1; i <=n; i++)
	{
		f[i] = i;

	}
	for (int i = 1; i <=m ; i++)
	{
		cin >> x >> y;
		int fx = find(x);
		int fy = find(y);
		if (fx!=fy)
		{
			f[fx] = fy;//合并操作

		}

	}
	for (int i = 1; i <=p ; i++)
	{
		cin >> x >> y;
		int fx = find(x);
		int fy = find(y);
		if (fx==fy)
		{
			cout << "Yes" << "\n";
		}
		else
		{
			cout << "No" << "\n";
		}

	}



}

[BOI2003] 团伙

题目描述

现在有 \(n\) 个人，他们之间有两种关系：朋友和敌人。我们知道：

  • 一个人的朋友的朋友是朋友
  • 一个人的敌人的敌人是朋友

现在要对这些人进行组团。两个人在一个团体内当且仅当这两个人是朋友。请求出这些人中最多可能有的团体数。

输入格式

第一行输入一个整数 \(n\) 代表人数。

第二行输入一个整数 \(m\) 表示接下来要列出 \(m\) 个关系。

接下来 \(m\) 行，每行一个字符 \(opt\) 和两个整数 \(p,q\)，分别代表关系（朋友或敌人），有关系的两个人之中的第一个人和第二个人。其中 \(opt\) 有两种可能：

  • 如果 \(opt\) 为 F，则表明 \(p\) 和 \(q\) 是朋友。
  • 如果 \(opt\) 为 E，则表明 \(p\) 和 \(q\) 是敌人。

输出格式

一行一个整数代表最多的团体数。

样例 #1

样例输入 #1

1
2
3
4
5
6
6
4
E 1 4
F 3 5
F 4 6
E 1 2

样例输出 #1

1
3

提示

对于 \(100\%\) 的数据，\(2 \le n \le 1000\)，\(1 \le m \le 5000\)，\(1 \le p,q \le n\)。

[NOI2001] 食物链

题目描述

动物王国中有三类动物 \(A,B,C\)，这三类动物的食物链构成了有趣的环形。\(A\) 吃 \(B\)，\(B\) 吃 \(C\)，\(C\) 吃 \(A\)。

现有 \(N\) 个动物，以 \(1 \sim N\) 编号。每个动物都是 \(A,B,C\) 中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这 \(N\) 个动物所构成的食物链关系进行描述：

  • 第一种说法是 1 X Y，表示 \(X\) 和 \(Y\) 是同类。
  • 第二种说法是2 X Y，表示 \(X\) 吃 \(Y\)。

此人对 \(N\) 个动物，用上述两种说法，一句接一句地说出 \(K\) 句话，这 \(K\) 句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

  • 当前的话与前面的某些真的话冲突，就是假话；
  • 当前的话中 \(X\) 或 \(Y\) 比 \(N\) 大，就是假话；
  • 当前的话表示 \(X\) 吃 \(X\)，就是假话。

你的任务是根据给定的 \(N\) 和 \(K\) 句话，输出假话的总数。

输入格式

第一行两个整数，\(N,K\)，表示有 \(N\) 个动物，\(K\) 句话。

第二行开始每行一句话（按照题目要求，见样例）

输出格式

一行，一个整数，表示假话的总数。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5

样例输出 #1

1
3

提示

对于全部数据，\(1\le N\le 5 \times 10^4\)，\(1\le K \le 10^5\)。

种类并查集的一般应用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for(int i=a;i<=n;i++)
const int N=5e6;
using ll=long long;
int n,m;
int f[N];
int find(int x)
{
	if (x==f[x])
	{
		return x;
	}
	return f[x]=find(f[x]);
}
int main()
{
cin>>n>>m;
rep(i,1,2*n)
{
	f[i]=i;
}
		char c;
		int a,b;
rep(i,1,m)
	{
		cin>>c>>a>>b;
		if(c=='F')
		{
			f[find(a)]=find(b);
		}
		else
		{
			f[find(a+n)]=find(b);
			f[find(b+n)]=find(a);
            //核心
		}
	}
	int ans=0;
	rep(i,1,n)
	{
		if(f[i]==i)
		{
			ans++;
            //找祖先是自己的就可以知道分类的
		}
	}
	cout<<ans;
}

[NOIP2004 提高组] 合并果子 / [USACO06NOV] Fence Repair G

题目描述

在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。

每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过 \(n-1\) 次合并之后， 就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为 \(1\) ，并且已知果子的种类 数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。

例如有 \(3\) 种果子，数目依次为 \(1\) ， \(2\) ， \(9\) 。可以先将 \(1\) 、 \(2\) 堆合并，新堆数目为 \(3\) ，耗费体力为 \(3\) 。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为 \(12\) ，耗费体力为 \(12\) 。所以多多总共耗费体力 \(=3+12=15\) 。可以证明 \(15\) 为最小的体力耗费值。

输入格式

共两行。
第一行是一个整数 \(n(1\leq n\leq 10000)\) ，表示果子的种类数。

第二行包含 \(n\) 个整数，用空格分隔，第 \(i\) 个整数 \(a_i(1\leq a_i\leq 20000)\) 是第 \(i\) 种果子的数目。

输出格式

一个整数，也就是最小的体力耗费值。输入数据保证这个值小于 \(2^{31}\) 。

样例 #1

样例输入 #1

1
2
3 
1 2 9

样例输出 #1

1
15

提示

对于 \(30\%\) 的数据，保证有 \(n \le 1000\)：

对于 \(50\%\) 的数据，保证有 \(n \le 5000\)；

对于全部的数据，保证有 \(n \le 10000\)。

最小堆的应用

如果不是相邻的就会变成区间dp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<bits/stdc++.h>
using namespace std;
const int N=1e7;
#define rep(i,a,n) for(int i=a;i<=n;i++)
priority_queue <int,vector<int>,greater<int> >q;
int main()
{
int n,x,y;
int ans=0;
int cost;
cin>>n;
rep(i,1,n)
{
    cin>>x;
    q.push(x);
}
while(q.size()>1)
{
    x=q.top();
q.pop();
    y=q.top();
q.pop();
cost =x+y;
q.push(cost);
ans+=cost;
}
cout<<ans;


}

求m区间内的最小值

题目描述

一个含有 \(n\) 项的数列，求出每一项前的 \(m\) 个数到它这个区间内的最小值。若前面的数不足 \(m\) 项则从第 \(1\) 个数开始，若前面没有数则输出 \(0\)。

输入格式

第一行两个整数，分别表示 \(n\)，\(m\)。

第二行，\(n\) 个正整数，为所给定的数列 \(a_i\)。

输出格式

\(n\) 行，每行一个整数，第 \(i\) 个数为序列中 \(a_i\) 之前 \(m\) 个数的最小值。

样例 #1

样例输入 #1

1
2
6 2
7 8 1 4 3 2

样例输出 #1

1
2
3
4
5
6
0
7
7
1
1
3

提示

对于 \(100\%\) 的数据，保证 \(1\le m\le n\le2\times10^6\)，\(1\le a_i\le3\times10^7\)。

单调队列裸题罢了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for(int i=a;i<=n;i++)
const int N=5e6;
using ll=long long;
int a[N];
struct node
{
	int val;
	int pos;
}b[N];
int ans[N];
int main()
{
int n,m;
cin>>n>>m;
rep(i,1,n)
{
	cin>>a[i];
}
int head=1;
int tail=0;
ans[0]=0;
rep(i,1,n-1)
{
	while(head<=tail&&b[tail].val>a[i])
	{
		tail--;
	}
    b[++tail].val=a[i];
    b[tail].pos=i;
	while((head <= tail)&&(b[head].pos < i - m+1))
            {
			head++;
			}
        ans[i] = b[head].val;
}
rep(i,0,n-1)
{
	cout<<ans[i]<<"\n";
}
}

琪露诺

题目描述

在幻想乡，琪露诺是以笨蛋闻名的冰之妖精。

某一天，琪露诺又在玩速冻青蛙，就是用冰把青蛙瞬间冻起来。但是这只青蛙比以往的要聪明许多，在琪露诺来之前就已经跑到了河的对岸。于是琪露诺决定到河岸去追青蛙。

小河可以看作一列格子依次编号为 \(0\) 到 \(N\)，琪露诺只能从编号小的格子移动到编号大的格子。而且琪露诺按照一种特殊的方式进行移动，当她在格子 \(i\) 时，她只移动到区间 \([i+L,i+R]\) 中的任意一格。你问为什么她这么移动，这还不简单，因为她是笨蛋啊。

每一个格子都有一个冰冻指数 \(A_i\)，编号为 \(0\) 的格子冰冻指数为 \(0\)。当琪露诺停留在那一格时就可以得到那一格的冰冻指数 \(A_i\)。琪露诺希望能够在到达对岸时，获取最大的冰冻指数，这样她才能狠狠地教训那只青蛙。

但是由于她实在是太笨了，所以她决定拜托你帮它决定怎样前进。

开始时，琪露诺在编号 \(0\) 的格子上，只要她下一步的位置编号大于 \(N\) 就算到达对岸。

输入格式

第一行三个正整数 \(N, L, R\)。

第二行共 \(N+1\) 个整数，第 \(i\) 个数表示编号为 \(i-1\) 的格子的冰冻指数 \(A_{i-1}\)。

输出格式

一个整数，表示最大冰冻指数。

样例 #1

样例输入 #1

1
2
5 2 3
0 12 3 11 7 -2

样例输出 #1

1
11

提示

对于 \(60\%\) 的数据，\(N \le 10^4\)。

对于 \(100\%\) 的数据，\(N \le 2\times 10^5\)，$-10^3 A_i^3 $，$1 L R N $。数据保证最终答案不超过 \(2^{31}-1\)。

dp方程很好写

由于要记录跳过来区间里面的最大值进行转移，于是可以考虑单调队列进行优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define frep(i, a, n) for (int i = a; i >= n; i--)
using namespace std;
const int N=1e7;
int a[N];
int f[N];
int que[N];
int h=0;
int t=0;
const int INF = 2e9;
int ans = -INF;
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int n,l,r;
    cin>>n>>l>>r;
    memset(f, 128, sizeof(f));
    f[0]=0;
    rep(i,0,n)
    {
        cin>>a[i];
    }
    rep(i,l,n)
    {
        while (que[h] + r < i && t >= h)
        {
            h++;
        }
        while(f[i-l]>f[que[t]]&&t>=h)
        {
            t--;
        }
        que[++t]=i-l;
        f[i]=f[que[h]]+a[i];
        if(i+r>n)
        {
            ans=max(ans,f[i]);
        }
    }
cout<<ans;
}

X(or)-mas Tree

题面翻译

给定一颗 \(n(n\le 2\times 10^5)\) 个点的带权树，一些权值已经确定而其他的没有确定（用 \(-1\) 表示）。

现在有 \(m(m\le 2\times 10^5)\) 条信息表示 \(u_i\) 到 \(v_i\) 的路径上的权值 \(\texttt{xor}\) 和的 popcount 为奇数还是偶数。

请你构造出这样一棵树，或者输出无解。

题目描述

'Twas the night before Christmas, and Santa's frantically setting up his new Christmas tree! There are $ n $ nodes in the tree, connected by $ n-1 $ edges. On each edge of the tree, there's a set of Christmas lights, which can be represented by an integer in binary representation.

He has $ m $ elves come over and admire his tree. Each elf is assigned two nodes, $ a $ and $ b $ , and that elf looks at all lights on the simple path between the two nodes. After this, the elf's favorite number becomes the bitwise XOR of the values of the lights on the edges in that path.

However, the North Pole has been recovering from a nasty bout of flu. Because of this, Santa forgot some of the configurations of lights he had put on the tree, and he has already left the North Pole! Fortunately, the elves came to the rescue, and each one told Santa what pair of nodes he was assigned $ (a_i, b_i) $ , as well as the parity of the number of set bits in his favorite number. In other words, he remembers whether the number of $ 1 $ 's when his favorite number is written in binary is odd or even.

Help Santa determine if it's possible that the memories are consistent, and if it is, remember what his tree looked like, and maybe you'll go down in history!

输入格式

The first line contains one integer $ t $ ( $ 1 t ^4 $ ) — the number of test cases. Then $ t $ cases follow.

The first line of each test case contains two integers, $ n $ and $ m $ ( $ 2 n ^5 $ ; $ 1 m ^5 $ ) — the size of tree and the number of elves respectively.

The next $ n-1 $ lines of each test case each contains three integers, $ x $ , $ y $ , and $ v $ ( $ 1 x, y n $ ; $ -1 v < 2^{30} $ ) — meaning that there's an edge between nodes $ x $ and $ y $ . If

  • $ v = -1 $ : Santa doesn't remember what the set of lights were on for this edge.
  • $ v $ : The set of lights on the edge is $ v $ .

The next $ m $ lines of each test case each contains three integers, $ a $ , $ b $ , and $ p $ ( $ 1 a, b n $ ; $ a b $ ; $ 0 p $ ) — the nodes that the elf was assigned to, and the parity of the number of set bits in the elf's favorite number.

It is guaranteed that the sum of all $ n $ and the sum of all $ m $ don't exceed $ 2 ^5 $ each.

It is guaranteed that the given edges form a tree.

输出格式

For each test case, first print either YES or NO (in any case), whether there's a tree consistent with Santa's memory or not.

If the answer is YES, print $ n-1 $ lines each containing three integers: $ x $ , $ y $ , and $ v $ ( $ 1 x, y n $ ; $ 0 v < 2^{30} $ ) — the edge and the integer on that edge. The set of edges must be the same as in the input, and if the value of some edge was specified earlier, it can not change. You can print the edges in any order.

If there are multiple answers, print any.

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
4
6 5
1 2 -1
1 3 1
4 2 7
6 3 0
2 5 -1
2 3 1
2 5 0
5 6 1
6 1 1
4 5 1
5 3
1 2 -1
1 3 -1
1 4 1
4 5 -1
2 4 0
3 4 1
2 3 1
3 3
1 2 -1
1 3 -1
1 2 0
1 3 1
2 3 0
2 1
1 2 1
1 2 0

样例输出 #1

1
2
3
4
5
6
7
8
9
10
11
12
13
YES
1 2 0
1 3 1
2 4 7
3 6 0
2 5 0
YES
1 2 1
1 3 0
1 4 1
4 5 1
NO
NO

提示

The first test case is the image in the statement.

One possible answer is assigning the value of the edge $ (1, 2) $ to $ 5 $ , and the value of the edge $ (2, 5) $ to $ 3 $ . This is correct because:

  • The first elf goes from node $ 2 $ to node $ 3 $ . This elf's favorite number is $ 4 $ , so he remembers the value $ 1 $ (as $ 4 $ has an odd number of $ 1 $ bits in its binary representation).
  • The second elf goes from node $ 2 $ to node $ 5 $ . This elf's favorite number is $ 3 $ , so he remembers the value $ 0 $ (as $ 3 $ has an even number of $ 1 $ bits in its binary representation).
  • The third elf goes from node $ 5 $ to node $ 6 $ . This elf's favorite number is $ 7 $ , so he remembers the value $ 1 $ (as $ 7 $ has an odd number of $ 1 $ bits in its binary representation).
  • The fourth elf goes from node $ 6 $ to node $ 1 $ . This elf's favorite number is $ 1 $ , so he remembers the value $ 1 $ (as $ 1 $ has an odd number of $ 1 $ bits in its binary representation).
  • The fifth elf goes from node $ 4 $ to node $ 5 $ . This elf's favorite number is $ 4 $ , so he remembers the number $ 1 $ (as $ 4 $ has an odd number of $ 1 $ bits in its binary representation).

Note that there are other possible answers.

有无解问题还是可以考虑一下并查集的

\(popcount(x \oplus y) \equiv popcount(x) \oplus popcount(y)\ (\text{mod}\ 2)\)

如果两个点的路径异或和popcount是奇数，那么这两个点到根节点路径异或和popcount奇偶性不同，反之相同。

于是转化成这样一个问题：有两个集合，每个条件描述如果为1，则这两个点在同一个集合，反之则不在一个集合。输入树的边的时候，如果边的popcount是奇数，那么边的两个端点不在一个集合，反之在一个集合。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
#include<bits/stdc++.h>
using namespace std;
const int N=1e6;
int fa[N];
vector<int>t[N],v[N];
int a[N];
int find(int x)
{
	if (x==fa[x]) return fa[x];
	return fa[x]=find(fa[x]);
}//并查集问题
int wq[N];
bool ans;
int wr(int z)
 //1的个数的奇偶性问题
{
	int res=0;
	while (z)
	{
		if (z&1) res^=1;
		z>>=1;
	}
	return res;
}
void merge(int x,int y)
{
	x=find(x),y=find(y);
	if (x==y) return;
	fa[x]=y;
}//并查集合并
int n,m;
void ddd(int x,int y,int z)
{
	if (z==0) 
	{
		if (find(x+n)==find(y)||find(y+n)==find(x))
		{
			ans=1;
			return;
		}
		merge(x,y),merge(x+n,y+n);
	}
	else
	{
		if (find(x)==find(y)||find(y+n)==find(x+n))
		{
			ans=1;
			return;
		}
		merge(x,y+n),merge(y,x+n);
	}
}
void dfs(int x,int f,int vv)
{
	if (x==1) a[x]=0,wq[find(1)]=0,wq[find(1+n)]=1;
	else 
	{
		if (wq[find(x)]==-1) 
		{
			a[x]=0;
			wq[find(x)]=0,wq[find(x+n)]=1;
		}
		else
		{
			a[x]=wq[find(x)];
		}
		if (vv!=-1)cout<<x<<' '<<f<<' '<<vv<<'\n';
		else cout<<x<<" "<<f<<' '<<(a[x]^a[f])<<'\n';
	}
	for (int i=0;i<t[x].size();i++)
	{
		if (t[x][i]==f) continue;
		dfs(t[x][i],x,v[x][i]);
	}
}
void work()
{
	int x,y,z;
	cin>>n>>m;
	ans=0;
	for (int i=1;i<=2*n;i++) fa[i]=i,wq[i]=-1;
	for (int i=1;i<=n;i++) t[i].clear();
	for (int i=1;i<=n;i++) v[i].clear();
	for (int i=1;i<n;i++)
	{
		cin>>x>>y>>z;
		t[x].push_back(y),t[y].push_back(x);
		v[x].push_back(z),v[y].push_back(z);
		if (z!=-1) ddd(x,y,wr(z));
	}
	for (int i=1;i<=m;i++)
	{
		cin>>x>>y>>z;
		ddd(x,y,z);
	}
	if (ans==1)
	{
	cout<<"NO"<<'\n';
		return;
	}
	a[1]=0;
cout<<"YES"<<'\n';
	dfs(1,-1,-1);
	return;
}
int main()
{
	int T;
	cin>>T;
	while (T--) work();
	return 0;
}

OpenStreetMap

题面翻译

给定一个 $ nm $ 的矩阵 $ h $ ,求出所有大小为 $ ab $ 的子矩形中的最小值的和.
矩阵的给定方式: 给定 $ g_0,x,y,z $ ,它们表示一个序列 $ g_i=(g_{i-1}x+y)z $ ,而 $ h_{i,j}=g_{(i-1)m+j-1} $.

题目描述

Seryozha conducts a course dedicated to building a map of heights of Stepanovo recreation center. He laid a rectangle grid of size $ n m $ cells on a map (rows of grid are numbered from $ 1 $ to $ n $ from north to south, and columns are numbered from $ 1 $ to $ m $ from west to east). After that he measured the average height of each cell above Rybinsk sea level and obtained a matrix of heights of size $ n m $ . The cell $ (i, j) $ lies on the intersection of the $ i $ -th row and the $ j $ -to column and has height $ h_{i, j} $ .

Seryozha is going to look at the result of his work in the browser. The screen of Seryozha's laptop can fit a subrectangle of size $ a b $ of matrix of heights ( $ 1 a n $ , $ 1 b m $ ). Seryozha tries to decide how the weather can affect the recreation center — for example, if it rains, where all the rainwater will gather. To do so, he is going to find the cell having minimum height among all cells that are shown on the screen of his laptop.

Help Seryozha to calculate the sum of heights of such cells for all possible subrectangles he can see on his screen. In other words, you have to calculate the sum of minimum heights in submatrices of size $ a b $ with top left corners in $ (i, j) $ over all $ 1 i n - a + 1 $ and $ 1 j m - b + 1 $ .

Consider the sequence $ g_i = (g_{i - 1} x + y) z $ . You are given integers $ g_0 $ , $ x $ , $ y $ and $ z $ . By miraculous coincidence, $ h_{i, j} = g_{(i - 1) m + j - 1} $ .

输入格式

The first line of the input contains four integers $ n $ , $ m $ , $ a $ and $ b $ ( $ 1 n, m ,000 $ , $ 1 a n $ , $ 1 b m $ ) — the number of rows and columns in the matrix Seryozha has, and the number of rows and columns that can be shown on the screen of the laptop, respectively.

The second line of the input contains four integers $ g_0 $ , $ x $ , $ y $ and $ z $ ( $ 0 g_0, x, y < z ^9 $ ).

输出格式

Print a single integer — the answer to the problem.

样例 #1

样例输入 #1

1
2
3 4 2 1
1 2 3 59

样例输出 #1

1
111

提示

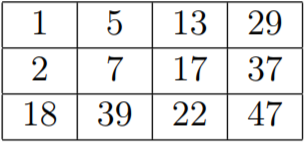
The matrix from the first example:

和理想正方形类似，不过本题存取会有点障碍，不过也可以硬模拟

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for(int i=a;i<=n;i++)
const int N=3005;
const int c=9e6+10;
using ll=long long;
int n,m,a,b;
ll g0,x,y,z;
ll g[c];
ll h[N][N];
ll q[N];
ll k[N][N];
int main()
{
cin>>n>>m>>a>>b;
	cin>>g[0]>>x>>y>>z;
	rep(i,1,n*m)
	{
	g[i]=(g[i-1]*x+y)%z;	
	 } 
rep(i,1,n)
{
	rep(j,1,m)
	{
	 h[i][j]=g[(i-1)*m+j-1];	
	 }
	}
//第一步：求每一行的最小值用单调队列
rep(i,1,n)
{
	int head=0;
	int tail=0;
	rep(j,1,m)
	{
		while(head<tail&&q[head]+b<=j)
		{
		head++;
		}
		while(head<tail&&h[i][q[tail-1]]>h[i][j])
		{
			tail--;
		}
		q[tail]=j;
		tail++;
		if(j>=b)
		{
			k[i][j-b+1]=h[i][q[head]];
		}	
	}	
}
rep(i,1,m-b+1)
{
	int head=0;
	int tail=0;
	rep(j,1,n)
	{
		while(head<tail&&q[head]+a<=j)
		{
			head++;
		}
		while(head<tail&&k[q[tail-1]][i]>k[j][i])
		{
			tail--;
		}
		q[tail]=j;
		tail++;
		if(j>=a)
		{
			h[j-a+1][i]=k[q[head]][i];
		}
	}
	
}
ll sum=0;
rep(i,1,n-a+1)
{
	rep(j,1,m-b+1)
	{
		sum+=h[i][j];
	}
	
}
cout<<sum;
//第二步：求每一列的最小值用单调队列

}