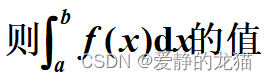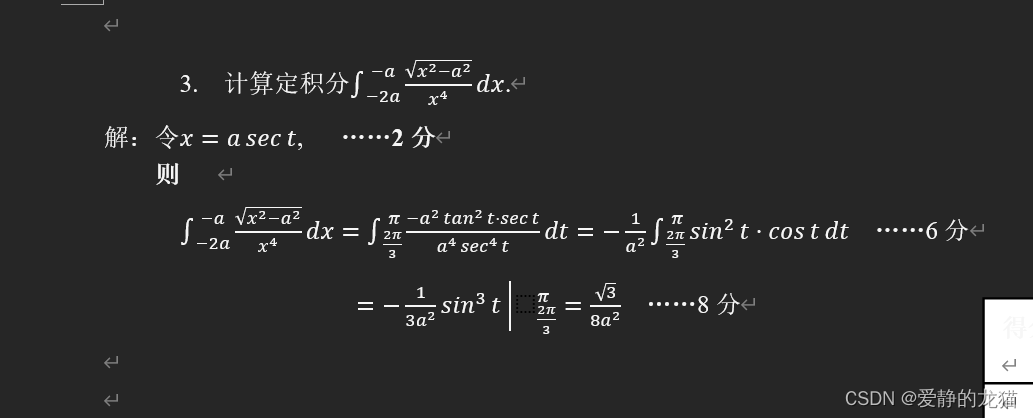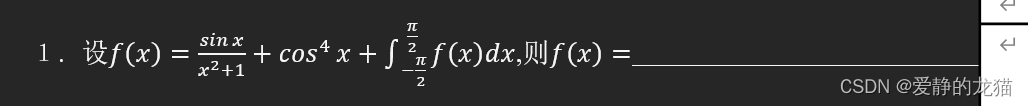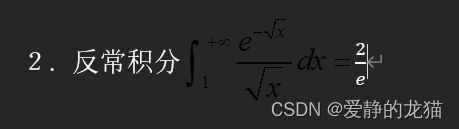工科数学分析上
工科数学分析上
CSDN上写的拿来救一下下学期的自己,顺便勉励自己再写一篇.....
----------------引言
第一节 集合与实数集
比较重要的是实数具有稠密性。
即在两个实数之间存在无穷个其他实数,
然后是绝对值不等式

第一个经常用来放缩不等式,证明极限
第二个则在一道课后题出现过,证明拿到a+2b的好像是(找到原题了)
这道题需要将我们要证明的点泰勒展开,然后用三角不等式,比较难(我不看答案不会写)

伯努利不等式

平均值不等式

再掌握一下左邻域和右邻域的表示方法,可能会作为第一题出现



还有一个就是确界原理,
一个非空有上(下)界的数集必存在上(下)确界.
不过不怎么考就是说,感觉上界下界的应用集中在那个单调有界收敛定理,而不是只是证明个上确界。
比如这种题
设 $ x_1 = 5 \(,\) x_n = $,其中 $ n = 2, 3, $。
求: $ _{n } x_n $
这样排版清晰了吗?如果有需要进一步调整或解答,请告诉我!
先证明有上界:
x1<5成立
假设xn<5
则xn+1<5。
再证明单增,除过去,根据刚刚结论即可
再两边取无穷就行
感觉泥工就喜欢考这个,不过这道比较常规。
还有一些留在单调有界那里罢。


第二节 映射与函数
不见得会考什么满射,单射,一一单射。
满射就是y全部有对应
单射就是每个X对应的y不一样
后者就是两个都有

有一种判断函数是否相同的题型,注意定义域和一些其他的就行。

上面是换元思想的初步体现
下面有一个比较重要的函数


完全相同的
有一道比较坑的题目,贴出来记忆一下罢。
这一部分考试基本不出题(我觉得)
第一节 函数极限的概念
主要是这
其中

一个与之相反的定义,不过我还是认为这个题没他位置

一道例题,了解一下就行
题型:
函数极限 $ _{x -} f(x) = A $ 的 \(\varepsilon\)-\(X\) 定义为:
- 对于任意的 $ G > 0 $,存在 $ > 0 $,使得对于所有满足 $ -< x - x_0 < 0 $ 的 $ x $,有 $ f(x) < -G $。
额外说明:
- 函数值无穷引入 $ G $。
- 定义域无穷引入 $ N $。
- 左邻域在表达时加上负号 \(-\)。
如果还有调整需求,可以随时告诉我!

注意上一章节讲述的左极限和右极限的书写,还有本题的不等式放缩,都是上一章的内容。
还有一种题型会考到,就是左右极限相等才连续,一般结合可导一起考察。

这道进行有理化之后可以进行适当的放缩,然后即可。

这道也是标准的做法,这里应该是默认n>=1了,当成数列了应该是,不然这样放估计有点问题。
第二节 数列极限的概念

函数极限与数列极限的关系
海涅定理的精髓感觉就是我可以取子列证反。
一般是取两个子列,各自趋近于正无穷,来证伪。
第三节 极限的运算法则
感觉没什么好讲的啊(蒟蒻保命)
感觉会无穷小,会有理化,应该就差不多了,偶尔需要个取对(这个经常考)。
比较需要注意的可能反而是渐近线。
三条渐近线理解一下。




泰勒公式求极限,实际上这题可以换n分之一为t然后进行洛必达,可以一试。

这里需要用到积分的换元才能做下去,积分的策略是必须求导,然后观察。
还有一道和这道一样的,也是需要先把里面的令成u才能做

洛必达之后进行倒变换可以换成一类重要极限

求极限:
$ _{x } $
先无穷小再泰勒.
极限
- 本题就需要变成e为底的,再化简采用洛必达等方法
- 下面这个直接洛必达就行
- 极限
;
也是先等价无穷小再进行洛必达,因为有积分


洛必达就可以。
第四节 极限的性质与两个重要极限
夹逼性,和保号性可能会考
两个重要极限注意代换即可
一般都是直接考上面那一种题型了
无穷小部分主要夹杂在这之中。
第五节 实数基本定理
一、单调有界收敛定理
经常考

可以先求出x2判断一下单调性,然后再进行证明。
这样不至于连求上界还是下界都不知道。
我们这样目标就很明确,就是求下界和单调减少,
xn>0显然下界就有了。
本题单调不太好求出,需要进行一个递推,才能证明得出,之后取极限即可。

同样也是,我们可以求出x2判断出是单调减少,xn又大于等于根号2,就先有下界了,然后求单减就比较好求了,总体步骤就是这样。

显然xn单增,这是可以观察得到的,但上界如何证明呢?
a+xn>xn的平方
那么可以证明有上界,再取极限就行了。
致密性定理:每个有界数列都有收敛的子列
用的比较多的实际上是他的逆定理。

柯西收敛

第七节、连续与间断

可能会考分段函数那块。
三类分段点
第一类,左右极限都存在,就是可去或跳跃
第二类:左右极限至少有一个不存在,无穷或振荡
最难的还是接下来这一部分
第八节 连续函数的性质
有界性:闭区间连续必当有界
最大最小值定理:闭区间连续必有最大值最小值
零点存在定理:异号中间有根
介值定理:两个函数值之间的任一函数值必有一x与之对应

康托定理在一致连续性的应用往往是用康托定理缩小范围。
理论其实就这些,题目看看具体怎么考
第一道题目:一致连续性结合拉格朗日进行考察,因为我们这时候已经没办法化成正常的x1-x2了,必须借助拉格朗日了
经过拉格朗日的放缩后就可以出现我们需要的x1-x2了。

第二题:拉格朗日+一致连续

第三题:构造e的x次方*x然后零点存在性定理就可

第四题:
采用和差化积,然后就可以进行放缩
提供公式如下


第五题:康托定理和子列的选取和一致连续
由于康托定理则第一个成立
然后取两个子列,就可以了。
取两个子列相减趋近于0,然后证明大于所谓的一波斯诺就行了。
第六题:介值定理
运用在后半部分,由于他肯定介于最大值最小值之间,所以一定有一个(可喜)位于(可喜1)和(可喜2)之间

第七题:好像是罗尔定理,有点串场了
不过讲解一下构造函数
构造x*f(x)
然后还需要积分中值定理,得到F(1)=F(可喜)
然后用罗尔定理,这部分请看第三章后再看。

第八题:构造和PPT一题一样

然后又拉格朗日即可
第九题:还是拉格朗日加上一致连续



由于条件就可以得到部分一致连续,再由于康托定理又一部分连续,则全部连续
第一,二,三节 导数的概念, 函数的求导法则,隐函数的导数和参数式求导
主要定义,有时候极限洛必达后可能会出现定义的写法,这时候不能再洛下去了,必须结合定义求解
还有,对于在单独一个点的导数也需要结合定义。
可导等价于左导数等于右导数


极坐标式求导

对r和角度乘积求导
习题1:

求n阶导数的应用,可以消去一些部分
习题2:
隐函数求导注意一下即可,
第二点:求解二阶导的时候如果是参数方程,要注意÷x对t的求导

第三题:实际应用题:设有光强度为a与b的两个光源,它们之间的距离是d. 假定照度与光强度成正比而与距离的平方成反比. 试问在两光源之间的直线段上什么地方其光的照度最小?
建模求导就行

第四题:同样是隐函数求导

只需要进行求出导数带进去即可
第五题:参数方程求导

注意重新÷就行。
第六题:参数方程求导:
- 椭圆
在t=π4处的切线方程为:
;
第七题:隐函数求导但是需要先取对数不然头大

第8题:实际应用题 编辑
也是建模后求导即可
第9题:求n阶导数
和第一题一样

第十题:求n阶导

有点巧妙,学到了
第十一题:参数方程的求导

第十二题:依然n阶导,和上面一样

第五节 微分中值定理与泰勒公式



带皮亚诺余项的

带拉格朗日余项的

函数的性态研究
主要是求两个导数
求出驻点和拐点,判断图像
注意渐近线和无穷处的极限不能漏掉
同时凹凸函数的部分性质需要掌握,比如凸函数切线都在下方,还有中间点的函数值偏小,二阶导此刻大于0
第一题:拉格朗日的运用

第二题:列表题目,正常必定会有,百分百

先判断定义域,求驻点和拐点,列表,绘图即可,如果不要求画图的

第三题:还是一样的拉格朗日啊,真没变

第四题:这题设那个点x0为最小值的点,由费马定理自然有导函数为0,然后自然就可以在该点展开,后就可以进行讨论,就恒成立。
第五题:函数性态

第六题:画出图像

第七题:
第一题:求二阶导大于0就可凸函数。
第二题:构造b*x<x的p次方/p+b的q次方/q则进行求导带入
第八题:
求导

第九题:
第二个问的第二个问不太好证明,背一下把(bushi)

第四章 积分


估值用的,我想也不会考

积分第一中值定理



牛顿莱布尼兹

注意如果t混入x要么换元要么提出去
还要一类十定积分的应用,或者说表示
k/n时候当初x
好比这题,i/n当初x写就行了

掌握不定积分的三种求法和有理函数的求法,和三角有关思考变形或者万能或者分步
反常积分实际上和上面没什么太大区别一般还是正常求
几何上的应用在公式基础上变形即可
物理应用不太可能考
面积公式


体积公式:

后两个为绕着y轴旋转


已知截面

弧长:



侧面积

还有两种同上
一大波题目来袭:
第一道题:

两边同时取积分
第一项奇函数消去,第二项用三角变换,倍角公式
第二道题:
先把e-x移动进去,再把1+e-x移动进去,然后分步积分,后一部分的积分用换元可以求出
换元是把e-x换掉,也可以等式上下×e的x次方,然后移动进去一个,这种方法更好。

第三题:

答案直接换了,我的话应该是会化为x=secx,然后变换的,化成后会变成你认识的积分的
这就是我的写法。

第三道题:常规换元求解即可
第四道题:求面积
注意是0到4分之Π


第五道题目:求解体积
这题无法死记忆公式,只能够分析
用绕y轴的公式进行变形才行

第六道题:和上面一题一样套路
第七题:想不到就先分步积分罢,能看到一样的

第八题:
采用第三个面积公式。
第九题:

第九题则是需要将区间分割为两部分分别运用第一个面积公式,不然会有负数
第十题:分步一次积分,有规律
然后就可以猜出来了.......

第十一题:
第一种做法自然是直接硬算,然后会有重复的一项
另一种你可以万能替换
分母1-t的平方
如果是cos就是1+t平方
如果是sin,就是2t
移出来是2

第十二题:建议用第一种方法一劳永逸
第十三题:
没看出和普通有什么区别,正常算就好了
第十四题:典型分部积分
第十五题:
分子分母速速同时×e的x次方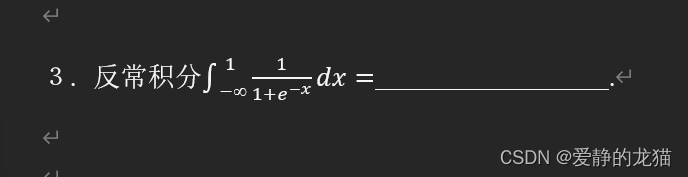

只需要换个元就可以,可以观察到x分之一的罢
第十七题:一样用第三个体积公式即可

第十八题:你需要分成两部分,进行计算,还有1-cosx=2sin2x/2然后进行分部积分
原题x-sinx/1-cosx(忘记截屏)
第十九题:第一题直接隐函数求导,第二题的用第一个面积公式记得先把化简出来

第20题:运用到了保号性

假设一点为0,则在一个(可喜)邻域里面他必大于0,然后用区间的可加性,这个答案写的不那么仔细,严格应该是3段区间都要写出来,放缩掉2段才行

第21和22题
第一题可以像他这样分步,也可以用半角
第二题就是直接用面积的第二个公式即可

第23题:极坐标的求导不多见,可以康康,极坐标的弧长也是不多见,可以康康

第24题:比较巧妙,我建议我背下来(bushi)

世间温柔,不过是芳春柳摇染花香,槐序蝉鸣入深巷,白茂叶落醉故乡。

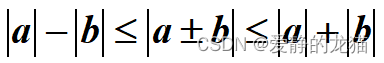


 ;
;
 在t=π4处的切线方程为:
在t=π4处的切线方程为: ;
;