【算法2-2】常见优化技巧

评价算法的标准，除了正确性以外，最重要的就是程序的运行效率是否足够高，是否可以在限定的时间内处理完指定的数据。在“暴力枚举”一章中介绍了可以通过剔除无效操作来提升算法效率。除此之外，还可以用“单调性”和“空间换时间”来优化时间复杂度。将这两种思想结合，产生了单调栈和单调队列等工具。

这些技巧可以帮助我们排除无效选项，在一定范围内保持单调性，常常可以将一些问题求解的时间复杂度降到O(n)，因此称为线性时间复杂度优化。

A-B 数对

题目背景

出题是一件痛苦的事情！

相同的题目看多了也会有审美疲劳，于是我舍弃了大家所熟悉的 A+B Problem，改用 A-B 了哈哈！

题目描述

给出一串正整数数列以及一个正整数 $C$，要求计算出所有满足 $A - B = C$ 的数对的个数（不同位置的数字一样的数对算不同的数对）。

输入格式

输入共两行。

第一行，两个正整数 $N,C$。

第二行，$N$ 个正整数，作为要求处理的那串数。

输出格式

一行，表示该串正整数中包含的满足 $A - B = C$ 的数对的个数。

样例 #1

样例输入 #1

1 2	4 1 1 1 2 3

样例输出 #1

提示

对于 $75\%$ 的数据，$1 \leq N \leq 2000$。

对于 $100\%$ 的数据，$1 \leq N \leq 2 \times 10^5$，$0 \leq a_i <2^{30}$，$1 \leq C < 2^{30}$。

2017/4/29 新添数据两组

这个呢就是找到第一个大于或等于他的和第一个大于他的

类似于二分做法？

后两种做法来自题解

#include<bits/stdc++.h>
using namespace std;
const int N=1e7;
int a[N];
using ll=long long;
#define rep(i,a,n) for(int i=a;i<=n;i++)
int main()
{
int n;
cin>>n;
int  c;
cin>>c;
rep(i,1,n)
{
    cin>>a[i];
}
sort(a+1,a+1+n);
int l=0;
int r=0;
ll ans=0;
rep(i,1,n)
{
    while(a[i]>a[l]-c&&l<=n )
    {
        l++;
    }
    while(a[i]>=a[r]-c&&r<=n)
   {
    r++;
   }
   if(a[l]-a[i]==c)
   {
       ans += r - l;
   }
}
cout<<ans;
}

真正的二分做法

#include<bits/stdc++.h>
using namespace std;
long a[200001];
long N,C,ans;
int main()
{
    cin>>N>>C;
    for(int i=1;i<=N;i++)
    {
        cin>>a[i];
    }
    sort(a+1,a+N+1);
    for(int i=1;i<=N;i++)
    {
        ans+=((upper_bound(a+1,a+N+1,a[i]+C)-a)-(lower_bound(a+1,a+N+1,a[i]+C)-a));
    }
    cout<<ans;
    return 0;
}

哈希做法

 #include <iostream>
    #include <map>
    using namespace std;
    typedef long long LL;
    LL a[200001];
    map<LL,LL> m;//建立一个数字到出现次数的映射 map<num,times>
    //A-B=C --> A-C=B
    int main() {
        int n;
        LL c;
        LL ans=0;
        cin >> n >> c;
        for(int i=1;i<=n;i++) {
            cin >> a[i];
            m[a[i]]++;
            a[i]-=c;    
        } 
        for(int i=1;i<=n;i++) ans+=m[a[i]];
        cout << ans << endl;
        return 0;
}

逛画展

题目描述

博览馆正在展出由世上最佳的 $m$ 位画家所画的图画。

游客在购买门票时必须说明两个数字，$a$ 和 $b$，代表他要看展览中的第 $a$ 幅至第 $b$ 幅画（包含 $a,b$）之间的所有图画，而门票的价钱就是一张图画一元。

Sept 希望入场后可以看到所有名师的图画。当然，他想最小化购买门票的价格。

请求出他购买门票时应选择的 $a,b$，数据保证一定有解。

若存在多组解，输出 $a$ 最小的那组。

输入格式

第一行两个整数 $n,m$，分别表示博览馆内的图画总数及这些图画是由多少位名师的画所绘画的。

第二行包含 $n$ 个整数 $a_i$，代表画第 $i$ 幅画的名师的编号。

输出格式

一行两个整数 $a,b$。

样例 #1

样例输入 #1

1 2	12 5 2 5 3 1 3 2 4 1 1 5 4 3

样例输出 #1

2 7

提示

数据规模与约定

对于 $30\%$ 的数据，有 $n\le200$，$m\le20$。
对于 $60\%$ 的数据，有 $n\le10^5$，$m\le10^3$。
对于 $100\%$ 的数据，有 $1\leq n\le10^6$，$1 \leq a_i \leq m\le2\times10^3$。

滑动窗口罢

出现新的画师把计数器加一，直到看到所有画师的画，这时候就可以左移缩小范围了，如果弹出的画只出现了一次,sum--

用两个变量来记录当前区间左右端点作为初始答案

通俗一点：

如果l到r的区间不满足要求,r++

如果l到r的区间满足要求,记录答案,l++

#include<bits/stdc++.h>
using namespace std;
const int N=1e7;
#define rep(i,a,n) for(int i=a;i<=n;i++)
int a[N];
int f[N];
int ans=1e9;
int ansl;
int ansr;
int main()
{
    int n,m;
    cin>>n>>m;
rep(i,1,n)
{
    cin>>a[i];
}
int  l=1,r=1;
int sum=1;
f[a[1]]=1;
while(l<=r&&r<=n)
{
    if(sum==m)
    {
        if(ans>r-l+1)
            //这里不算等于，因为要满足输出a最小的一组
        {
            ans=r-l+1;
            ansl=l;
            ansr=r;
        }
        f[a[l]]--;
        if(f[a[l]]==0)
        {
            sum--;
        }
        l++;
    }
     else
     {
        r++;
        f[a[r]]++;
        if(f[a[r]]==1)
        {
            sum++;
        }
     }
}
cout << ansl << ' ' << ansr;
}

最大子段和

题目描述

给出一个长度为 $n$ 的序列 $a$，选出其中连续且非空的一段使得这段和最大。

输入格式

第一行是一个整数，表示序列的长度 $n$。

第二行有 $n$ 个整数，第 $i$ 个整数表示序列的第 $i$ 个数字 $a_i$。

输出格式

输出一行一个整数表示答案。

样例 #1

样例输入 #1

1 2	7 2 -4 3 -1 2 -4 3

样例输出 #1

提示

样例 1 解释

选取 $[3, 5]$ 子段 $\{3, -1, 2\}$，其和为 $4$。

数据规模与约定

对于 $40\%$ 的数据，保证 $n \leq 2 \times 10^3$。
对于 $100\%$ 的数据，保证 $1 \leq n \leq 2 \times 10^5$，$-10^4 \leq a_i \leq 10^4$。

这个题就一句话，如果加上这个数比这个数还小，那就把前面扔了吧

#include <bits/stdc++.h>
using namespace std;
const int N = 1e7;
#define rep(i, a, n) for (int i = a; i <= n; i++)
using ll=long long;
int a;
int main()
{
int n;
cin>>n;
int f=0;
int ans=-999999999;
rep(i,1,n)
{
cin>>a;
f=max(f+a,a);
//如果加上比这个值本身还小，加他干什么呢
ans=max(f,ans);
//维护作用
}
cout<<ans;
}

[CSP-J2020] 直播获奖

题目描述

NOI2130 即将举行。为了增加观赏性，CCF 决定逐一评出每个选手的成绩，并直播即时的获奖分数线。本次竞赛的获奖率为 $w\%$，即当前排名前 $w\%$ 的选手的最低成绩就是即时的分数线。

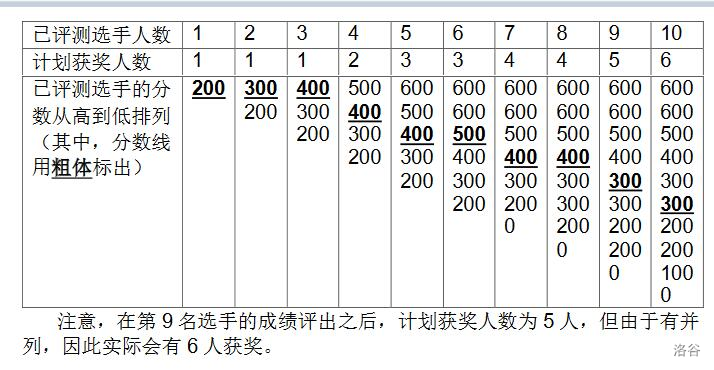
更具体地，若当前已评出了 $p$ 个选手的成绩，则当前计划获奖人数为 $\max(1, \lfloor p \times w \%\rfloor)$，其中 $w$ 是获奖百分比，$\lfloor x \rfloor$ 表示对 $x$ 向下取整，$\max(x,y)$ 表示 $x$ 和 $y$ 中较大的数。如有选手成绩相同，则所有成绩并列的选手都能获奖，因此实际获奖人数可能比计划中多。

作为评测组的技术人员，请你帮 CCF 写一个直播程序。

输入格式

第一行有两个整数 $n, w$。分别代表选手总数与获奖率。
第二行有 $n$ 个整数，依次代表逐一评出的选手成绩。

输出格式

只有一行，包含 $n$ 个非负整数，依次代表选手成绩逐一评出后，即时的获奖分数线。相邻两个整数间用一个空格分隔。

样例 #1

样例输入 #1

1 2	10 60 200 300 400 500 600 600 0 300 200 100

样例输出 #1

1	200 300 400 400 400 500 400 400 300 300

样例 #2

样例输入 #2

1 2	10 30 100 100 600 100 100 100 100 100 100 100

样例输出 #2

1	100 100 600 600 600 600 100 100 100 100

提示

样例 1 解释

he ---

数据规模与约定

各测试点的 $n$ 如下表：

测试点编号	$n=$
$1 \sim 3$	$10$
$4 \sim 6$	$500$
$7 \sim 10$	$2000$
$11 \sim 17$	$10^4$
$18 \sim 20$	$10^5$

对于所有测试点，每个选手的成绩均为不超过 $600$ 的非负整数，获奖百分比 $w$ 是一个正整数且 $1 \le w \le 99$。

提示

在计算计划获奖人数时，如用浮点类型的变量（如 C/C++ 中的 float 、 double，Pascal 中的 real 、 double 、 extended 等）存储获奖比例 $w\%$，则计算 $5 \times 60\%$ 时的结果可能为 $3.000001$，也可能为 $2.999999$，向下取整后的结果不确定。因此，建议仅使用整型变量，以计算出准确值。

破解之法：分数的范围非常小（只有600）

#include <bits/stdc++.h>
using namespace std;
const int N = 1e7;
#define rep(i, a, n) for (int i = a; i <= n; i++)
using ll = long long;
int a[N];
int main()
{
int tmp;
int n,w;
cin>>n>>w;
for(int i=1;i<=n;i++)
{
    cin>>tmp;
    a[tmp]++;
    int sum=0;
    for(int j=600;j>=0;j--)
    {
        sum+=a[j];
        if(sum>=max(1,i*w/100))
        {
            cout<<j<<' ';
            break;
        }
    }
}
    return 0;
}

[NOIP2015 普及组] 求和

题目背景

NOIP2015 普及组 T3

题目描述

一条狭长的纸带被均匀划分出了 $n$ 个格子，格子编号从 $1$ 到 $n$。每个格子上都染了一种颜色 $color_i$ 用 $[1,m]$ 当中的一个整数表示），并且写了一个数字 $number_i$。

编号	1	2	3	4	5	6
颜色和数字	$\color{blue}{5}$	$\color{blue}{5}$	$\color{red}{3}$	$\color{red}{2}$	$\color{blue}{2}$	$\color{red}{2}$

定义一种特殊的三元组：$(x,y,z)$，其中 $x,y,z$ 都代表纸带上格子的编号，这里的三元组要求满足以下两个条件：

$x,y,z$ 都是整数，$x<y<z,y-x=z-y$。
$color_x=color_z$。

满足上述条件的三元组的分数规定为 $(x+z) \times (number_x+number_z)$。整个纸带的分数规定为所有满足条件的三元组的分数的和。这个分数可能会很大，你只要输出整个纸带的分数除以 $10007$ 所得的余数即可。

输入格式

第一行是用一个空格隔开的两个正整数 $n$ 和 $m,n$ 表纸带上格子的个数，$m$ 表纸带上颜色的种类数。

第二行有 $n$ 用空格隔开的正整数，第 $i$ 个数字表示纸带上编号为 $i$ 格子上面写的数字 $number_i$。

第三行有 $n$ 用空格隔开的正整数，第 $i$ 数字表示纸带上编号为 $i$ 格子染的颜色 $color_i$。

输出格式

一个整数，表示所求的纸带分数除以 $10007$ 所得的余数。

样例 #1

样例输入 #1

1
2
3

6 2
5 5 3 2 2 2
2 2 1 1 2 1

样例输出 #1

样例 #2

样例输入 #2

1
2
3

15 4
5 10 8 2 2 2 9 9 7 7 5 6 4 2 4
2 2 3 3 4 3 3 2 4 4 4 4 1 1 1

样例输出 #2

提示

样例 1 解释

纸带如题目描述中的图所示。

所有满足条件的三元组为：$(1, 3, 5), (4, 5, 6)$。

所以纸带的分数为 $(1 + 5) \times (5 + 2) + (4 + 6) \times (2 + 2) = 42 + 40 = 82$。

对于第 $1$ 组至第 $2$ 组数据， $1 ≤ n ≤ 100, 1 ≤ m ≤ 5$；

对于第 $3$ 组至第 $4$ 组数据，$1 ≤ n ≤ 3000, 1 ≤ m ≤ 100$；

对于第 $5$ 组至第 $ 6 $ 组数据，$1 ≤ n ≤ 100000, 1 ≤ m ≤ 100000$，且不存在出现次数超过 $ 20 $ 的颜色；

对于全部 $10$ 组数据，$1 ≤ n ≤ 100000, 1 ≤ m ≤ 100000, 1 ≤ color_i ≤ m,1≤number_i≤100000$。

读完题后可以发现题目中的y是没有作用的，他唯一的限制只是限制了奇数和奇数相加，偶数与偶数相加罢了。

接下来是进行计算

这样实际上就转换了问题

我们只需要会求一种颜色，其他颜色也会求

琢磨公式就可以发现，要用前缀和（）好好琢磨罢

#include<bits/stdc++.h>
using namespace std;
using ll=long  long;
#define rep(i,a,n) for(int i=a;i<=n;i++)
const int N=1e6;
const int mod=10007;
int a[N];
int b[N];
int s1[N][3];
int s2[N][3];
int ans;
int main()
{
    int n,m;
    cin>>n>>m;
    rep(i,1,n)
    {
        cin>>a[i];
    }
    rep(i,1,n)
    {
        cin>>b[i];
        s1[b[i]][i%2]++;
        //记录同种颜色的个数
        s2[b[i]][i%2]=(s2[b[i]][i%2]+a[i])%mod;
        //记录同种颜色的总和
     }
    rep(i,1,n)
{
ans+=(i*((s2[b[i]][i%2]-a[i])+a[i]*(s1[b[i]][i%2]-1)%mod))%mod;
ans%=mod;
}
cout<<ans%mod;
}

介绍一种算法（解决极大子矩形的问题）本篇的奶牛浴场也属于此类问题，不过解决方法与本题不同

有效竖线：除了两个端点外，不覆盖任何障碍点的竖直线段。

悬线：上端点覆盖了一个障碍点或达到整个矩形上端的有效竖线。如图所示的三个有效竖线都是悬线。

【定理3】：如果将一个悬线向左右两个方向尽可能移动所得到的有效子矩形称为这个悬线所对应的子矩形，那么所有悬线所对应的有效子矩形的集合一定包含了所有极大子矩形的集合。

我们需要知道有关于它的三个量：顶部、左右最多能移动到的位置。对于底部为(i,j)的悬线，设它的高为hight[i,j],左右最多能移动到的位置为left[i,j],right[i,j]。为了充分利用以前得到的信息，我们将这三个函数用递推的形式给出。

见下代码：

玉蟾宫

题目背景

有一天，小猫 rainbow 和 freda 来到了湘西张家界的天门山玉蟾宫，玉蟾宫宫主蓝兔盛情地款待了它们，并赐予它们一片土地。

题目描述

这片土地被分成 $N\times M$ 个格子，每个格子里写着 'R' 或者 'F'，R 代表这块土地被赐予了 rainbow，F 代表这块土地被赐予了 freda。

现在 freda 要在这里卖萌。。。它要找一块矩形土地，要求这片土地都标着 'F' 并且面积最大。

但是 rainbow 和 freda 的 OI 水平都弱爆了，找不出这块土地，而蓝兔也想看 freda 卖萌（她显然是不会编程的……），所以它们决定，如果你找到的土地面积为 $S$，它们每人给你 $S$ 两银子。

输入格式

第一行两个整数 $N$，$M$，表示矩形土地有 $N$ 行 $M$ 列。

接下来 $N$ 行，每行 $M$ 个用空格隔开的字符 'F' 或 'R'，描述了矩形土地。

输出格式

输出一个整数，表示你能得到多少银子，即 ($3\times \text{最大 'F' 矩形土地面积}$) 的值。

样例 #1

样例输入 #1

5 6 
R F F F F F 
F F F F F F 
R R R F F F 
F F F F F F 
F F F F F F

样例输出 #1

提示

对于 $50\%$ 的数据，$1 \leq N, M \leq 200$。
对于 $100\%$ 的数据，$1 \leq N, M \leq 1000$。

//一个极大矩形应该是上下左右都不能再向外扩充的矩形。
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define frep(i,a,n) for(int i=a;i>=n;i--)
const int N=1010;
char a[N][N];
int r[N][N];
int l[N][N];
int h[N][N];
int ans=0;
int main()
{
    int n,m;
    cin>>n>>m;
        //初始化
    rep(i,1,n)
    {
        rep(j,1,m)
        {
            cin>>a[i][j];
            h[i][j]=1;//高度初始化为1
            l[i][j]=r[i][j]=j;
            //宽度初始化为他当前的位置
        }
    }
    rep(i,1,n)
    {
    rep(j,2,m)
    {
        if(a[i][j]=='F'&&a[i][j-1]=='F')
        {
            l[i][j]=l[i][j-1];
        }
    }
        frep(j,m-1,1)
    {
    if(a[i][j+1]=='F'&&a[i][j]=='F')
    {
    r[i][j]=r[i][j+1];
    }
    }
    }
rep(i,2,n){
    rep(j,1,m)
    {
        if(a[i][j]=='F'&&a[i-1][j]=='F')
        {
            h[i][j]=h[i-1][j]+1;
            if(l[i-1][j]>l[i][j])
            {
                l[i][j]=l[i-1][j];
            }
            if(r[i-1][j]<r[i][j])
            {
r[i][j]=r[i-1][j];
            }
        }
    }
}
rep(i,1,n)
{
    rep(j,1,m)
    {
        if(a[i][j]=='F'&&((r[i][j]-l[i][j]+1)*h[i][j])>ans)
        {
            ans=(r[i][j]-l[i][j]+1)*h[i][j];
        }
    }
}
cout<<3*ans;


}

[USACO06NOV] Bad Hair Day S

题目描述

农夫约翰有 $N$ 头奶牛正在过乱头发节。

每一头牛都站在同一排面朝右，它们被从左到右依次编号为 $1, 2, \cdots, N$。编号为 $i$ 的牛身高为 $h_i$。第 $N$ 头牛在最前面，而第 $1$ 头牛在最后面。

对于第 $i$ 头牛前面的第 $j$ 头牛，如果 $h_i>h_{i+1}, h_i>h_{i+2}, \cdots, h_i>h_j$，那么认为第 $i$ 头牛可以看到第 $i+1$ 到第 $j$ 头牛。

定义 $C_i$ 为第 $i$ 头牛所能看到的牛的数量。请帮助农夫约翰求出 $C _ 1 + C _ 2 + \cdots + C _ N$。

输入格式

输入共 $N + 1$ 行。

第一行为一个整数 $N$，代表牛的个数。
接下来 $N$ 行，每行一个整数 $a _ i$，分别代表第 $1, 2, \cdots, N$ 头牛的身高。

输出格式

输出共一行一个整数，代表 $C _ 1 + C _ 2 + \cdots + C _ N$。

样例 #1

样例输入 #1

样例输出 #1

提示

数据规模与约定

对于 $100\%$ 的数据，保证 $1 \leq N \leq 8 \times 10 ^ 4$，$1 \leq h _ i \leq 10 ^ 9$。

这是单调栈的经典应用，与其看到几头牛，，不如算能被几头牛看到

单调栈弹出

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
#define re register
#define rep(i,a,n) for(re int i=a;i<=n;i++)
#define frep(i,a,n) for(re int i=a;i>=n;i--)
ll ans;
int main()
{
	ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n;
cin>>n;
stack<ll>s;
rep(i,1,n){
	ll t;
	cin>>t;
	while(!s.empty()&&s.top()<=t)
	{
		s.pop();
	}
	ans+=s.size();
	s.push(t);
	
}
cout<<ans;
}

长方形

题目描述

小明今天突发奇想，想从一张用过的纸中剪出一个长方形。

为了简化问题，小明做出如下规定：

（1）这张纸的长宽分别为 $n,m$。小明将这张纸看成是由$n\times m$个格子组成，在剪的时候，只能沿着格子的边缘剪。

（2）这张纸有些地方小明以前在上面画过，剪出来的长方形不能含有以前画过的地方。

（3）剪出来的长方形的大小没有限制。

小明看着这张纸，想了好多种剪的方法，可是到底有几种呢？小明数不过来，你能帮帮他吗？

输入格式

第一行两个正整数 $n,m$，表示这张纸的长度和宽度。

接下来有 $n$ 行，每行 $m$ 个字符，每个字符为 * 或者 .。

字符 * 表示以前在这个格子上画过，字符 . 表示以前在这个格子上没画过。

输出格式

仅一个整数，表示方案数。

样例 #1

样例输入 #1

6 4
....
.***
.*..
.***
...*
.***

样例输出 #1

提示

【数据规模】

对 $10\%$ 的数据，满足 $1\leq n\leq 10,1\leq m\leq 10$

对 $30\%$ 的数据，满足 $1\leq n\leq 50,1\leq m\leq 50$

对 $100\%$ 的数据，满足 $1\leq n\leq 1000,1\leq m\leq 1000$ $$ 使用单调栈算出

l i 和

r i ，分别是 ℎ 中左边第一个（从

h i 开始）不大于 ℎ

i 的数和右边第一个（从 ℎ

i 开始）小于 ℎ

i 的数 $$

$$ 对每一列求出被这一列的高度限制的长方形数，即为(

−

l i ) × (

r i

−

× ℎ

i 将所有列的答案相加就是以当前行为底边构造的长方形的方案数了 $$

//定义h数组，h[i][j]表示第i行第j列最多可以向上延伸多长
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
#define rep(i, a, n) for ( int i = a; i <= n; i++)
#define frep(i, a, n) for ( int i = a; i >= n; i--)
const  int N=1e3+10;
char a[N][N];
int h[N][N];
int r[N];
int l[N];
ll ans;
int st[N];
int main()
{
int n,m;
cin>>n>>m;
char c;
for ( int i = 1; i <= n; ++i)
{
    for ( int j = 1; j <= m; ++j)
    {
        cin >> c;
        if (c == '*')
            h[i][j] = 0;
        else
            h[i][j] = h[i - 1][j] + 1;
        //枚举这个点最多能够向上伸展多少
    }
}
for (int i = 1; i <= n; ++i)
    h[i][0] = h[i][m + 1] = -0x7fffffff;
int top=0;
rep(i,1,n)
{
    stack<int>s1;
    stack<int>s2;
    s1.push(1);
    s2.push(m);
    rep(j,2,m+1)
    {
        while(!s1.empty()&&h[i][j]<h[i][s1.top()])
        {
r[s1.top()]=j;
s1.pop();
        }
        s1.push(j);
    }
frep(j,m,0)
{
    while(!s2.empty()&&h[i][j]<=h[i][s2.top()])
    {
l[s2.top()]=j;
s2.pop();
    }
    s2.push(j);
}
rep(j,1,m)
{
    ans+=(r[j]-j)*(j-l[j])*h[i][j];
}
}
cout<<ans;
}

扫描

题目描述

有一个 $1 \times n$ 的矩阵，有 $n$ 个整数。

现在给你一个可以盖住连续 $k$ 个数的木板。

一开始木板盖住了矩阵的第 $1 \sim k$ 个数，每次将木板向右移动一个单位，直到右端与第 $n$ 个数重合。

每次移动前输出被覆盖住的数字中最大的数是多少。

输入格式

第一行两个整数 $n,k$，表示共有 $n$ 个数，木板可以盖住 $k$ 个数。

第二行 $n$ 个整数，表示矩阵中的元素。

输出格式

共 $n - k + 1$ 行，每行一个整数。

第 $i$ 行表示第 $i \sim i + k - 1$ 个数中最大值是多少。

样例 #1

样例输入 #1

1 2	5 3 1 5 3 4 2

样例输出 #1

1
2
3

5
5
4

提示

对于 $20\%$ 的数据，$1 \leq k \leq n \leq 10^3$。

对于 $50\%$ 的数据，$1 \leq k \leq n \leq 10^4$。

对于 $100\%$ 的数据，$1 \leq k \leq n \leq 2 \times 10^6$，矩阵中的元素大小不超过 $10^4$ 并且均为正整数。

单调队列模板提可以说是

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define frep(i, a, n) for (int i = a; i >= n; i--)
const int N = 1e6;
int a[N];
int q[N];
int n,k;
int main()
{
    cin>>n>>k;
    rep(i,1,n)
    {
        cin>>a[i];
    }
    int head=0;
    //头指针
    int tail=0;
    //尾指针
    rep(i,1,n)
    {
        while(head<tail&&q[head]<=i-k)
        {
            head++;
        }
        //一开始全部加进去
        while(head<tail&&a[q[tail-1]]<a[i])
        {
            tail--;
        }
        //如果头比较大，就弹走
        q[tail]=i;
        //塞进去
        tail++;
        //尾指针++
        if(i>=k)
            //如果能输出，输出队首
        {
            cout<<a[q[head]]<<'\n';
        }
    }
}

[HAOI2007] 理想的正方形

题目描述

有一个 $a \times b$ 的整数组成的矩阵，现请你从中找出一个 $n \times n$ 的正方形区域，使得该区域所有数中的最大值和最小值的差最小。

输入格式

第一行为 $3$ 个整数，分别表示 $a,b,n$ 的值。

第二行至第 $a+1$ 行每行为 $b$ 个非负整数，表示矩阵中相应位置上的数。每行相邻两数之间用一空格分隔。

输出格式

仅一个整数，为 $a \times b$ 矩阵中所有“ $n \times n$ 正方形区域中的最大整数和最小整数的差值”的最小值。

样例 #1

样例输入 #1

样例输出 #1

提示

问题规模。

矩阵中的所有数都不超过 $1,000,000,000$。

$20\%$ 的数据 $2 \le a,b \le 100,n \le a,n \le b,n \le 10$。

$100\%$ 的数据 $2 \le a,b \le 1000,n \le a,n \le b,n \le 100$。

单调队列维护最大

再维护最小

然后减去（）

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int m[N][N];
int q[N];
int rowmin[N][N];
int rowmax[N][N];
int colmin[N][N];
int colmax[N][N];
int a,b,n;
int ans=1000000000;
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define frep(i, a, n) for (int i = a; i >= n; i--)
int main()
{
cin>>a>>b>>n;
rep(i,1,a)
{
    rep(j,1,b)
    {
        cin>>m[i][j];
    }
}
rep(row,1,a)
{
    int  h=0;
     int t=0;
rep(i,1,b)
{
    while(h<t&&q[h]+n<=i)
    {
        h++;
    }
    while(h<t&&m[row][q[t-1]]<m[row][i])
    {
        t--;
    }
    q[t]=i;
    t++;
if(i>=n)
{
    rowmax[row][i-n+1]=m[row][q[h]];
}
}
h=0,t=0;
rep(i, 1, b)
{
    while (h < t && q[h]+n <=i )
    {
        h++;
    }
    while (h <t && m[row][q[t - 1]] > m[row][i])
    {
        t--;
    }
    q[t] = i;
    t++;
    if (i >= n)
    {
        rowmin[row][i - n + 1] = m[row][q[h]];
    }
}
}
rep(col,1,b-n+1)
{
  int   h=0;
    int t=0;
    rep(i,1,a)
    {
        while(h<t&&q[h]+n<=i)
        {
            h++;
        }
        while(h<t&&rowmax[q[t-1]][col]<rowmax[i][col])
        {
            t--;
        }
        q[t]=i;
        t++;
        if(i>=n)
        {
            colmax[i-n+1][col]=rowmax[q[h]][col];
        }
    }
     h=0;
    t=0;
    rep(i,1,a)
    {
        while(h<t&&q[h]+n<=i)
        {
            h++;
        }
        while(h<t&&rowmin[q[t-1]][col]>rowmin[i][col])
        {
            t--;
        }
        q[t]=i;
        t++;
        if(i>=n)
        {
            colmin[i-n+1][col]=rowmin[q[h]][col];
        }
    }
   
}

rep(i,1,a-n+1)
{
    rep(j,1,b-n+1)
    {
        if(colmax[i][j]-colmin[i][j]<ans)
        {
            ans=colmax[i][j]-colmin[i][j];
        }
    }
}
cout<<ans;
}

唯一的雪花 Unique Snowflakes

题面翻译

【题目描述】

企业家 Emily 有一个很酷的主意：把雪花包起来卖。她发明了一台机器，这台机器可以捕捉飘落的雪花，并把它们一片一片打包进一个包裹里。一旦这个包裹满了，它就会被封上送去发售。

Emily 的公司的口号是“把独特打包起来”，为了实现这一诺言，一个包裹里不能有两片一样的雪花。不幸的是，这并不容易做到，因为实际上通过机器的雪花中有很多是相同的。Emily 想知道这样一个不包含两片一样的雪花的包裹最大能有多大，她可以在任何时候启动机器，但是一旦机器启动了，直到包裹被封上为止，所有通过机器的雪花都必须被打包进这个包裹里，当然，包裹可以在任何时候被封上。

【输入格式】

第一行是测试数据组数 $T$，对于每一组数据，第一行是通过机器的雪花总数 $n$（$n \le {10}^6$），下面 $n$ 行每行一个在 $[0, {10}^9]$ 内的整数，标记了这片雪花，当两片雪花标记相同时，这两片雪花是一样的。

【输出格式】

对于每一组数据，输出最大包裹的大小。

题目描述

PDF

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

#include<bits/stdc++.h>

using namespace std;
const int N=1000005;

int t, n, a[N], last[N];

unordered_map<int, int> vis;   
//哈希，一个非常妙的地方
void Solve(){
  cin >> t;
    //输入
  while(t--)
  {
    cin >> n;
    for(int i = 1; i <= n; i++)
    {
      cin >> a[i];
    }
      
    for(int i = 1; i <= n; i++)
    {    
      if(!vis[a[i]]){   
        last[i] = -1;
          //如果还没访问，上一个记作-1，这样就可以知道他第一次出现
      }
      else{
        last[i] = vis[a[i]];   
          //不然就记录上一次出现的位置
      }
      vis[a[i]] = i;    
        //不断更新出现的位置
    }
    int l = 1, r = 1, maxi = -1e9;
      //首尾指针
    while(r <= n){     
      while(r <= n && l > last[r])
      {    
        r++;
          //如果l比当前r指向的元素的上一个元素出现的晚就不断++
      }
      maxi = max(maxi, r - l);  
        //记录，因为此时是没有出现重复的
      l++;
        //因为再走出现重复了，l++，康康能不能消除这种重复
    }
    cout << maxi << '\n';
    vis.clear();   
  }
}

int main(){
  Solve();
}

[CEOI2017] Sure Bet

题目描述

现在有 $n$ 个A类灯泡和 $n$ 个B类灯泡，每个灯泡都有各自的权值。

我们将这些灯泡分为 $n$ 组，每组包含一个来自A类的灯泡和一个来自B类的灯泡。

你可以从中选取任意个灯泡，每选取一个灯泡需要花费 $1$ 的代价。

在你选取完之后，系统会随机在A类和B类中选择一个类型，并点亮那一类的所有灯泡。你选取的每个点亮的灯泡会给你带来等于它权值的收益。

现在请你合理选取灯泡，以最大化可能的最小收益。你只需要求出来这个收益即可。

输入格式

第一行一个正整数 $n$ ，表示灯泡的组数。

接下来 $n$ 行每行两个空格隔开的实数 $A_i,B_i$。分别表示属于这组的A灯泡和B灯泡的权值。输入的实数不会超过四位小数。

输出格式

输出最大化的最小可能收益，请输出到小数点后恰好四位。

样例 #1

样例输入 #1

4
1.4 3.7
1.2 2
1.6 1.4
1.9 1.5

样例输出 #1

0.5000

提示

样例解释

最优策略是选择第一组的B灯泡和第三组的A灯泡和第四组的A灯泡：

如果B类灯泡被点亮，收益是 $3.7-3=0.7$。
如果A类灯泡被点亮，收益是 $1.6+1.9-3=0.5$ 。

最小可能收益是 $0.5$。

数据范围

对于所有测试点，有 $1.0\le A_i,B_i\le 1000.0$，$0\le n\le 10^5$。

#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define frep(i, a, n) for (int i = a; i >= n; i--)
const int N=1e6;
double  a[N];
double b[N];
bool cmp(double a,double b)
{
    return a>b;
}
int main()
{
    int n;
    cin>>n;
    rep(i,1,n)
    {
        cin>>a[i]>>b[i];
    }
sort(a+1,a+1+n,cmp);
sort(b+1,b+1+n,cmp);
rep(i,1,n)
{
    a[i]+=a[i-1];
    b[i]+=b[i-1];
}
double ans=0;
int l=1;
int r=1;
   //因为要使得最小值尽可能的大
    //我们一开始肯定就要往大了选
    //但是如果A选的过于大的话，那你这时候是不是要选B，因为你最后的答案是由小的那一类决定的，因此你要使得AB类尽可能的平均，所以预处理方面，我们需要对AB进行从大到小的排序，然后做一个前缀和，因为我们选一个的话最大的那个肯定要选，选两个的话，最大的那两个也一定要选，3个同理，n个也同理，因此实际上我们可以再进一步的优化，做一个前缀和。
    //预处理工作做完了，接下来就是双指针的操作空间了
    //r代表b选了几个数
    //l代表a选了几个数
while(l<=n&&r<=n)
{
    if(a[l]>b[r])
        //如果a比较大，那么选b
    {
ans=max(ans,b[r]-l-r);
r++;
    }
    //如果b比较大，那么选a
    else{
ans=max(ans,a[l]-l-r);
l++;
}
}
printf("%.4lf", ans);
    //输出ans
return 0;
}

[USACO16OPEN] Diamond Collector S

题目描述

Bessie the cow, always a fan of shiny objects, has taken up a hobby of mining diamonds in her spare time! She has collected $N$ diamonds ($N \leq 50,000$) of varying sizes, and she wants to arrange some of them in a pair of display cases in the barn.

Since Bessie wants the diamonds in each of the two cases to be relatively similar in size, she decides that she will not include two diamonds in the same case if their sizes differ by more than $K$ (two diamonds can be displayed together in the same case if their sizes differ by exactly $K$). Given $K$, please help Bessie determine the maximum number of diamonds she can display in both cases together.

奶牛Bessie很喜欢闪亮亮的东西（Baling_Baling），所以她喜欢在她的空余时间开采钻石！她现在已经收集了N颗不同大小的钻石（N<=50,000），现在她想在谷仓的两个陈列架上摆放一些钻石。

Bessie想让这些陈列架上的钻石保持相似的大小，所以她不会把两个大小相差K以上的钻石同时放在一个陈列架上（如果两颗钻石的大小差值不大于K，那么它们可以同时放在一个陈列架上）。现在给出K，请你帮Bessie确定她最多一共可以放多少颗钻石在这两个陈列架上。

输入格式

The first line of the input file contains $N$ and $K$ ($0 \leq K \leq 1,000,000,000$).

The next $N$ lines each contain an integer giving the size of one of the

diamonds. All sizes will be positive and will not exceed $1,000,000,000$.

输出格式

Output a single positive integer, telling the maximum number of diamonds that

Bessie can showcase in total in both the cases.

样例 #1

样例输入 #1

样例输出 #1

#include <bits/stdc++.h>
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define frep(i, a, n) for (int i = a; i >= n; i--)
using namespace std;
const int maxn = 50000 + 5;
int n, k, a[maxn];
int pre[maxn], suf[maxn];
int main()
{
    cin>>n>>k;
    for (int i = 1; i <= n; ++i)
  cin>>a[i];
    sort(a + 1, a + 1 + n);
    int l, r;
    l = r = 1;
    for (r = 1; r <= n; ++r)
    {
        while (a[r] - a[l] > k)
            l++;
        pre[r] = r - l + 1;
        pre[r] = max(pre[r], pre[r - 1]);
    }
    //向左能伸长多长
    //需要加一个最大值记录
    l = r = n;
    for (l = n; l >= 1; --l)
    {
        while (a[r] - a[l] > k)
            r--;
        suf[l] = r - l + 1;
    }
    int ans = 0;
    for (int i = 1; i <= n; ++i)
    {
        ans = max(ans, suf[i] + pre[i - 1]);
    }
  cout<<ans;
    return 0;
}
//求出向左能伸长多少，向右能伸长多少，但是向左伸长的时候需要注意，我们实际上并不一只差距一个身位，我们可以隔好几个的左去选择。

[CSP-J 2021] 插入排序

题目描述

插入排序是一种非常常见且简单的排序算法。小 Z 是一名大一的新生，今天 H 老师刚刚在上课的时候讲了插入排序算法。

假设比较两个元素的时间为 $\mathcal O(1)$，则插入排序可以以 $\mathcal O(n^2)$ 的时间复杂度完成长度为 $n$ 的数组的排序。不妨假设这 $n$ 个数字分别存储在 $a_1, a_2, \ldots, a_n$ 之中，则如下伪代码给出了插入排序算法的一种最简单的实现方式：

这下面是 C/C++ 的示范代码：

for (int i = 1; i <= n; i++)
	for (int j = i; j >= 2; j--)
		if (a[j] < a[j-1]) {
			int t = a[j-1];
			a[j-1] = a[j];
			a[j] = t;
		}

这下面是 Pascal 的示范代码：

for i:=1 to n do
	for j:=i downto 2 do
		if a[j]<a[j-1] then
			begin
				t:=a[i];
				a[i]:=a[j];
				a[j]:=t;
			end;

为了帮助小 Z 更好的理解插入排序，小 Z 的老师 H 老师留下了这么一道家庭作业：

H 老师给了一个长度为 $n$ 的数组 $a$，数组下标从 $1$ 开始，并且数组中的所有元素均为非负整数。小 Z 需要支持在数组 $a$ 上的 $Q$ 次操作，操作共两种，参数分别如下：

$1~x~v$：这是第一种操作，会将 $a$ 的第 $x$ 个元素，也就是 $a_x$ 的值，修改为 $v$。保证 $1 \le x \le n$，$1 \le v \le 10^9$。注意这种操作会改变数组的元素，修改得到的数组会被保留，也会影响后续的操作。

$2~x$：这是第二种操作，假设 H 老师按照上面的伪代码对 $a$ 数组进行排序，你需要告诉 H 老师原来 $a$ 的第 $x$ 个元素，也就是 $a_x$，在排序后的新数组所处的位置。保证 $1 \le x \le n$。注意这种操作不会改变数组的元素，排序后的数组不会被保留，也不会影响后续的操作。

H 老师不喜欢过多的修改，所以他保证类型 $1$ 的操作次数不超过 $5000$。

小 Z 没有学过计算机竞赛，因此小 Z 并不会做这道题。他找到了你来帮助他解决这个问题。

输入格式

第一行，包含两个正整数 $n, Q$，表示数组长度和操作次数。

第二行，包含 $n$ 个空格分隔的非负整数，其中第 $i$ 个非负整数表示 $a_i$。

接下来 $Q$ 行，每行 $2 \sim 3$ 个正整数，表示一次操作，操作格式见【题目描述】。

输出格式

对于每一次类型为 $2$ 的询问，输出一行一个正整数表示答案。

样例 #1

样例输入 #1

样例输出 #1

1
2
3

1
1
2

提示

【样例解释 #1】

在修改操作之前，假设 H 老师进行了一次插入排序，则原序列的三个元素在排序结束后所处的位置分别是 $3, 2, 1$。

在修改操作之后，假设 H 老师进行了一次插入排序，则原序列的三个元素在排序结束后所处的位置分别是 $3, 1, 2$。

注意虽然此时 $a_2 = a_3$，但是我们不能将其视为相同的元素。

【样例 #2】

见附件中的 sort/sort2.in 与 sort/sort2.ans。

该测试点数据范围同测试点 $1 \sim 2$。

【样例 #3】

见附件中的 sort/sort3.in 与 sort/sort3.ans。

该测试点数据范围同测试点 $3 \sim 7$。

【样例 #4】

见附件中的 sort/sort4.in 与 sort/sort4.ans。

该测试点数据范围同测试点 $12 \sim 14$。

【数据范围】

对于所有测试数据，满足 $1 \le n \le 8000$，$1 \le Q \le 2 \times {10}^5$，$1 \le x \le n$，$1 \le v,a_i \le 10^9$。

对于所有测试数据，保证在所有 $Q$ 次操作中，至多有 $5000$ 次操作属于类型一。

各测试点的附加限制及分值如下表所示。

测试点	$n \le$	$Q \le$	特殊性质
$1 \sim 4$	$10$	$10$	无
$5 \sim 9$	$300$	$300$	无
$10 \sim 13$	$1500$	$1500$	无
$14 \sim 16$	$8000$	$8000$	保证所有输入的 $a_i,v$ 互不相同
$17 \sim 19$	$8000$	$8000$	无
$20 \sim 22$	$8000$	$2 \times 10^5$	保证所有输入的 $a_i,v$ 互不相同
$23 \sim 25$	$8000$	$2 \times 10^5$	无

#include <bits/stdc++.h>
using namespace std;
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define frep(i, a, n) for (int i = a; i >= n; i--)
using ll = long long;
const int N = 1e7;
int a[N];
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int n, q;
    cin >> n >> q;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    for (int i = 1; i <= q; i++)
    {
        int xx;
        cin >> xx;
        if (xx == 1)
        {
            int x, v;
            cin >> x >> v;
            a[x] = v;
        }
        //修改操作
        
        else
            //这个插入操作很有意思
        {
            int x;
         cin>>x;
            int w = a[x];
            int sum = n;
            for (int j = 1; j < x; j++)
            {
                if (a[j] > w)
                {
                    sum--;
                }
                //如果左边有比他大的，那么就要--，因为它可以往前走
            }
            for (int j = x + 1; j <= n; j++)
            {
                if (a[j] >= w)
                    //如果右边有大于等于他的，代表符合，也就是说不会改变顺序
                    sum--;
            }
           cout<<sum<<'\n';
        }
    }
    return 0;
}

奶牛浴场

题目描述

由于 John 建造了牛场围栏，激起了奶牛的愤怒，奶牛的产奶量急剧减少。为了讨好奶牛，John 决定在牛场中建造一个大型浴场。但是 John 的奶牛有一个奇怪的习惯，每头奶牛都必须在牛场中的一个固定的位置产奶，而奶牛显然不能在浴场中产奶，于是，John 希望所建造的浴场不覆盖这些产奶点。这回，他又要求助于 Clevow 了。你还能帮助 Clevow 吗？

John 的牛场和规划的浴场都是矩形。浴场要完全位于牛场之内，并且浴场的轮廓要与牛场的轮廓平行或者重合。浴场不能覆盖任何产奶点，但是产奶点可以位于浴场的轮廓上。

Clevow 当然希望浴场的面积尽可能大了，所以你的任务就是帮她计算浴场的最大面积。

输入格式

输入文件的第一行包含两个整数 $L$ 和 $W$，分别表示牛场的长和宽。

文件的第二行包含一个整数 $n$，表示产奶点的数量。

以下 $n$ 行每行包含两个整数 $x$ 和 $y$，表示一个产奶点的坐标。

所有产奶点都位于牛场内，即：$0 \le x \le L$，$0 \le y \le W$。

输出格式

输出文件仅一行，包含一个整数 $S$，表示浴场的最大面积。

样例 #1

样例输入 #1

样例输出 #1

提示

对于所有数据，$0 \le n \le 5 \times 10^3$，$1 \le L,W \le 3 \times 10^4$。

Winter Camp 2002

感谢 @凯瑟琳98 提供了 4 组 hack 数据。

下面是问题解决方案：

最大子矩形问题

背景：

给定一个含有障碍点的矩形，找出内部不含障碍点的、边与整个矩形平行或重合的最大子矩形。

有效子矩形：内部不包含任何障碍点且边界与坐标轴平行的子矩形。如图所示，第一个是有效子矩形（尽管边界上有障碍点），第二个不是有效子矩形（因为内部含有障碍点）。

极大子矩形：一个有效子矩形，如果不存在包含它且比它大的有效子矩形，就称这个有效子矩形为极大有效子矩形。最大子矩形：最大的有效子矩形。

最大子矩形 ⊆ ⊆ 极大子矩形 ⊆ ⊆ 有效子矩形

极大化思想

【定理1】在一个有障碍点的矩形中的最大子矩形一定是一个极大子矩形。

证明：如果最大子矩形A不是一个极大子矩形，那么根据极大子矩形的定义，存在一个包含A且比A更大的有效子矩形，这与“A是最大子矩形”矛盾，所以【定理1】成立。

因此，通过枚举所有的极大子矩形，就可以找到最大子矩形。

算法一：

纯玻璃，我们枚举的子举行不一定是极大有效子矩形，甚至不是有效子矩形，这是无用的，肯定需要进行优化。

（×）

【定理2】：一个极大子矩形的四条边一定都不能向外扩展。更进一步地说，一个有效子矩形是极大子矩形的充要条件是这个子矩形的每条边要么覆盖了一个障碍点，要么与整个矩形的边界重合。

正确性显然，

如果一个有效子矩形的某一条边既没有覆盖一个障碍点，又没有与整个矩形的边界重合，那么肯定存在一个包含它的有效子矩形。

算法二：

先枚举极大子矩形的左边界，然后从左到右依次扫描每一个障碍点，并不断修改可行的上下边界，从而枚举出所有以这个定点为左边界的极大子矩形。

这样做只考虑到了左边界覆盖一个点的矩形，因此我们还需要枚举左边界与整个矩形的左边界重合的情况。

种是左边界与整个举行的左边界重合，而右边界覆盖了一个障碍点的情况，对于这种情况，可以用类似的方法从右到左扫描每一个点作为右边界的情况。另一种是左右边界均与整个矩形的左右边界重合的情况，对于这类情况我们可以在预处理中完成：先将所有点按纵坐标排序，然后可以得到以相邻两个点的纵坐标为上下边界，左右边界与整个矩形的左右边界重合的矩形，显然这样的矩形也是极大子矩形，因此也需要被枚举到。

这样就可以了。

#include<bits/stdc++.h>
using namespace std;
struct S{//存放障碍点信息
	int x , y;
}s[5010];
bool cmp1(S a , S b)//按横坐标排序
{
	if(a.x != b.x) return a.x < b.x;
	else return a.y < b.y; 
}
bool cmp2(S a , S b)//按纵坐标排序
{
	if(a.y != b.y) return a.y < b.y;
	else return a.x < b.x ; 
}
int l , w , n , ans; 
int main()
{
   	cin>>l>>w>>n;   
    for(int i = 1; i <= n; i ++) cin>>s[i].x >> s[i].y;
    s[++ n].x = 0 , s[n].y = 0;//将四个顶点设为障碍点
	s[++ n].x = 0 , s[n].y = w;
	s[++ n].x = l , s[n].y = 0;
	s[++ n].x = l , s[n].y = w;
    int x1 , x2 , y1 , y2;//x1为左边界，x2为右边界,y1为下边界，y2为上边界
    //从左往右搜
    sort(s + 1 , s + n + 1 , cmp1);
    //一开始按照横坐标排序
    for(int i = 1; i <= n; i ++)
    {
    	x1 = s[i].x , y1 = 0 , y2 = w;
        //第一个点作为左边界，并依次向右
    	for(int j = i + 1; j <= n; j ++)
    	{
				x2 = s[j].x;
            //第二个点找到了
				ans = max(ans , (x2 - x1) * (y2 - y1));
            //先算答案
	    		if(s[j].y < s[i].y) y1 = max(y1 , s[j].y);//更新上下边界
	    	    else y2 = min(y2 , s[j].y); 
		}
	}
    //从右往左搜  
    for(int i = n; i >= 1; i --)
    {
    	x1 = s[i].x , y1 = 0 , y2 = w;
        //将最后一个点作为右边界向左枚举
    	for(int j = i - 1; j >= 1; j --)
    	{
	    		x2 = s[j].x;
				ans = max(ans , (x1 - x2) * (y2 - y1));
				if(s[j].y < s[i].y) y1 = max(y1 , s[j].y);
	    	    else y2 = min(y2 , s[j].y); 
		}
	}
	//处理特殊情况
	sort(s + 1 , s + n + 1 , cmp2); 
	for(int i = 1; i <= n - 1; i ++)
	{
		ans = max(ans , l * (s[i + 1].y - s[i].y));
	}
	//这个就是上面提到的，那个横轴都覆盖的情况
	cout<<ans;
}

[POI2008] PLA-Postering

题目描述

All the buildings in the east district of Byteburg were built in accordance with the old arbitecture:

they stand next to each other with no spacing inbetween.

Together they form a very long chain of buildings of diverse height, extending from east to west.

The mayor of Byteburg, Byteasar, has decided to have the north face of the chain covered with posters.

Byteasar ponders over the minimum number of posters sufficient to cover the whole north face.

The posters have rectangular shape with vertical and horizontal sides.

They cannot overlap, but may touch each other, i.e. have common points on the sides.

Every poster has to entirely adjoin the walls of certain buildings and the whole surface of the north face has to be covered.

Task Write a programme that:

reads the description of buildings from the standard input, determines the minimum number of posters needed to entirely cover their north faces, writes out the outcome to the standard output.

Byteburg市东边的建筑都是以旧结构形式建造的:建筑互相紧挨着,之间没有空间.它们共同形成了一条长长的,从东向西延伸的建筑物链(建筑物的高度不一).Byteburg市的市长Byteasar,决定将这个建筑物链的一侧用海报覆盖住.并且想用最少的海报数量,海报是矩形的.海报与海报之间不能重叠,但是可以相互挨着(即它们具有公共边),每一个海报都必须贴近墙并且建筑物链的整个一侧必须被覆盖(意思是:海报需要将一侧全部覆盖,并且不能超出建筑物链)

输入格式

The first line of the standard input contains one integer $n$ ($1\le n\le 250\ 000$), denoting the number of buildings the chain comprises of.

Each of the following $n$ lines contains two integers $d_i$ and $w_i$ ($1\le d_i,w_i\le 1\ 000\ 000\ 000$), separated by a single space, denoting respectively the length and height of the $i^{th}$ building in the row.

第一行为一个整数n(1≤n≤250000),表示有n个建筑,接下来n行中,第i行表示第i个建筑物的宽di与高wi(1≤di,wi≤1 000 000 000),中间由一个空格隔开

输出格式

The first and only line of the standard output should contain one integer, the minimum number of rectangular posters that suffice to cover the north faces of the buildings.

第一个为一个整数,表示最少需要几张海报.

样例 #1

样例输入 #1

样例输出 #1

提示

题目简述：N个矩形,排成一排. 现在希望用尽量少的矩形海报Cover住它们.

感谢@__乱世魇华提供翻译

因为题目要求海报不可超出建筑物链，那么我们即可用单调栈维护：初始海报数为建筑物数，入栈建筑物链的高度序列，当栈顶大于即将入栈元素时弹栈，若最后弹栈元素与即将入栈元素等高，需要的海报数-1；

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define frep(i, a, n) for (int i = a; i >= n; i--)
stack<ll>stk;
int n;
const int N=1e7;
ll num;
int a[N];
int main()
{
    cin>>n;
    int x;
    rep(i,1,n)
    {
        cin>>x>>a[i];
    }
    rep(i,1,n)
    {
        while(!stk.empty()&&stk.top()>a[i])
        {
            stk.pop();
        }
        if(stk.empty()||stk.top()<a[i])
        {
            num++;
        }
        stk.push(a[i]);
    }
cout<<num;
}

滑动窗口 /【模板】单调队列

题目描述

有一个长为 $n$ 的序列 $a$，以及一个大小为 $k$ 的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如，对于序列 $[1,3,-1,-3,5,3,6,7]$ 以及 $k = 3$，有如下过程：

\[\def\arraystretch{1.2} \begin{array}{|c|c|c|}\hline \textsf{窗口位置} & \textsf{最小值} & \textsf{最大值} \\ \hline \verb![1 3 -1] -3 5 3 6 7 ! & -1 & 3 \\ \hline \verb! 1 [3 -1 -3] 5 3 6 7 ! & -3 & 3 \\ \hline \verb! 1 3 [-1 -3 5] 3 6 7 ! & -3 & 5 \\ \hline \verb! 1 3 -1 [-3 5 3] 6 7 ! & -3 & 5 \\ \hline \verb! 1 3 -1 -3 [5 3 6] 7 ! & 3 & 6 \\ \hline \verb! 1 3 -1 -3 5 [3 6 7]! & 3 & 7 \\ \hline \end{array} \]

输入格式

输入一共有两行，第一行有两个正整数 $n,k$。第二行 $n$ 个整数，表示序列 $a$

输出格式

输出共两行，第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值

样例 #1

样例输入 #1

1 2	8 3 1 3 -1 -3 5 3 6 7

样例输出 #1

1 2	-1 -3 -3 -3 3 3 3 3 5 5 6 7

提示

【数据范围】
对于 $50\%$ 的数据，$1 \le n \le 10^5$；
对于 $100\%$ 的数据，$1\le k \le n \le 10^6$，$a_i \in [-2^{31},2^{31})$。

数组存下标，实现单调队列

#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define frep(i, a, n) for (int i = a; i >= n; i--)
using ll = long long;
const int N = 1e7;
int a[N];
int q[N];
int q2[N];
int main()
{
int n,m;
cin>>n>>m;
rep(i,1,n)
{
    cin>>a[i];
}
int h=1,t=0;
rep(i,1,n)
{
while (h <= t && q[h] + m <= i)
{
    h++;
}
    //如果头部下标<=i-m，证明已经可以弹出头部了
while (h <= t && a[i]<a[q[t]])
{
    t--;
}
    //如果说进来的值很小，就可以都弹出去了
q[++t] = i;
    //记录下来
if(i>=m)
{
    cout<<a[q[h]]<<' ';
}
    //可以输出就输出头部
    //下面同理，不解释
}
cout<<'\n';
 h = 1, t = 0;
rep(i, 1, n)
{

    while (h <= t && q2[h] + m <= i)
    {
        h++;
    }
    while (h <= t && a[i] > a[q2[t]])
    {
        t--;
    }
    q2[++t] = i;
    if (i >= m)
    {
        cout << a[q2[h]] << ' ';
    }
}
}

[USACO07JAN] Balanced Lineup G

题目描述

For the daily milking, Farmer John's N cows (1 ≤ N ≤ 50,000) always line up in the same order. One day Farmer John decides to organize a game of Ultimate Frisbee with some of the cows. To keep things simple, he will take a contiguous range of cows from the milking lineup to play the game. However, for all the cows to have fun they should not differ too much in height.

Farmer John has made a list of Q (1 ≤ Q ≤ 180,000) potential groups of cows and their heights (1 ≤ height ≤ 1,000,000). For each group, he wants your help to determine the difference in height between the shortest and the tallest cow in the group.

每天,农夫 John 的 $n(1\le n\le 5\times 10^4)$ 头牛总是按同一序列排队。

有一天, John 决定让一些牛们玩一场飞盘比赛。他准备找一群在队列中位置连续的牛来进行比赛。但是为了避免水平悬殊，牛的身高不应该相差太大。John 准备了 $q(1\le q\le 1.8\times10^5)$ 个可能的牛的选择和所有牛的身高 $h_i(1\le h_i\le 10^6,1\le i\le n)$。他想知道每一组里面最高和最低的牛的身高差。

输入格式

Line 1: Two space-separated integers, N and Q.

Lines 2..N+1: Line i+1 contains a single integer that is the height of cow i

Lines N+2..N+Q+1: Two integers A and B (1 ≤ A ≤ B ≤ N), representing the range of cows from A to B inclusive.

第一行两个数 $n,q$。

接下来 $n$ 行，每行一个数 $h_i$。

再接下来 $q$ 行，每行两个整数 $a$ 和 $b$，表示询问第 $a$ 头牛到第 $b$ 头牛里的最高和最低的牛的身高差。

输出格式

Lines 1..Q: Each line contains a single integer that is a response to a reply and indicates the difference in height between the tallest and shortest cow in the range.

输出共 $q$ 行，对于每一组询问，输出每一组中最高和最低的牛的身高差。

样例 #1

样例输入 #1

样例输出 #1

1
2
3

6
3
0

//ST表查询最大值和最小值模板
#include<bits/stdc++.h>
using namespace std;
const int N=50010;
int n,q,h[N],log_2[N],rmax[N][18],rmin[N][18];
void init()
{
    for(int i=1;i<=n;i++)
    {
        rmax[i][0]=rmin[i][0]=h[i];
    }
    for(int j=1;(1<<j)<=n;j++)
    {
        for(int i=1;i<=n-(1<<j)+1;i++)
        {
            rmax[i][j]=max(rmax[i][j-1],rmax[i+(1<<j -1)][j-1]);
            rmin[i][j]=max(rmin[i][j-1],rmin[i+(1<<j-1)][j-1]);
        }
    }
}
int query_max(int a,int b)
{
    int x=log_2[b-a+1];
    return max(rmax[a][x],rmax[b-(1<<x)+1][x]);
}
int query_min(int a, int b)
{
    int x = log_2[b - a + 1];
    return min(rmin[a][x], rmin[b - (1 << x) + 1][x]);
}
int main()
{
cin>>n>>q;
for(int i=1;i<=n;i++)
{
    cin>>h[i];
}
for(int i=2;i<=n;i++)
{
    log_2[i]=log_2[i>>1]+1;
}
init();
while(q--)
{
    int a,b;
    cin>>a>>b;
    cout<<query_max(a,b)-query_min(a,b)<<'\n';
}
}

切蛋糕

题目描述

今天是小 Z 的生日，同学们为他带来了一块蛋糕。这块蛋糕是一个长方体，被用不同色彩分成了 $n$ 个相同的小块，每小块都有对应的幸运值。

小 Z 作为寿星，自然希望吃到的蛋糕的幸运值总和最大，但小 Z 最多又只能吃 $m(m\le n)$ 小块的蛋糕。

请你帮他从这 $n$ 小块中找出连续的 $k(1 \le k\le m)$ 块蛋糕，使得其上的总幸运值最大。

形式化地，在数列 $\{p_n\}$ 中，找出一个子段 $l,r(r-l+1\le m)$，最大化 $\sum\limits_{i=l}^rp_i$。

输入格式

第一行两个整数 $n,m$。分别代表共有 $n$ 小块蛋糕，小 Z 最多只能吃 $m$ 小块。

第二行 $n$ 个整数，第 $i$ 个整数 $p_i$ 代表第 $i$ 小块蛋糕的幸运值。

输出格式

仅一行一个整数，即小 Z 能够得到的最大幸运值。

样例 #1

样例输入 #1

1 2	5 2 1 2 3 4 5

样例输出 #1

样例 #2

样例输入 #2

1 2	6 3 1 -2 3 -4 5 -6

样例输出 #2

提示

数据规模与约定

对于 $20\%$ 的数据，有 $1\le n\le100$。
对于 $100\%$ 的数据，有 $1\le n\le5\times 10^5$，$|p_i|≤500$。

保证答案的绝对值在 $[0,2^{31}-1]$ 之内。

前缀和+单调队列营造环境

#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define frep(i, a, n) for (int i = a; i >= n; i--)
using ll=long long;
const int N=1e6;
ll a[N];
ll sum[N];
ll q[N];
ll ans;
int main()
{
int n;
cin>>n;
int m;
cin>>m;
rep(i,1,n)
{
    cin>>a[i];
    sum[i]=sum[i-1]+a[i];
}
int t=0;
int h=0;
q[1]=0;
rep(i,1,n)
{
while(h<=t&&q[h]+m<i)
{
    h++;
}
ans=max(ans,sum[i]-sum[q[h]]);
while(h<=t&&sum[i]<=sum[q[t]])
{
    t--;
}
t++;
q[t]=i;
}
cout<<ans;
}

琪露诺

题目描述

在幻想乡，琪露诺是以笨蛋闻名的冰之妖精。

某一天，琪露诺又在玩速冻青蛙，就是用冰把青蛙瞬间冻起来。但是这只青蛙比以往的要聪明许多，在琪露诺来之前就已经跑到了河的对岸。于是琪露诺决定到河岸去追青蛙。

小河可以看作一列格子依次编号为 $0$ 到 $N$，琪露诺只能从编号小的格子移动到编号大的格子。而且琪露诺按照一种特殊的方式进行移动，当她在格子 $i$ 时，她只移动到区间 $[i+L,i+R]$ 中的任意一格。你问为什么她这么移动，这还不简单，因为她是笨蛋啊。

每一个格子都有一个冰冻指数 $A_i$，编号为 $0$ 的格子冰冻指数为 $0$。当琪露诺停留在那一格时就可以得到那一格的冰冻指数 $A_i$。琪露诺希望能够在到达对岸时，获取最大的冰冻指数，这样她才能狠狠地教训那只青蛙。

但是由于她实在是太笨了，所以她决定拜托你帮它决定怎样前进。

开始时，琪露诺在编号 $0$ 的格子上，只要她下一步的位置编号大于 $N$ 就算到达对岸。

输入格式

第一行三个正整数 $N, L, R$。

第二行共 $N+1$ 个整数，第 $i$ 个数表示编号为 $i-1$ 的格子的冰冻指数 $A_{i-1}$。

输出格式

一个整数，表示最大冰冻指数。

样例 #1

样例输入 #1

1 2	5 2 3 0 12 3 11 7 -2

样例输出 #1

提示

对于 $60\%$ 的数据，$N \le 10^4$。

对于 $100\%$ 的数据，$N \le 2\times 10^5$，$-10^3 A_i^3 $，$1 L R N $。数据保证最终答案不超过 $2^{31}-1$。 \[ f[i]=max(f[j])+A[i] (i−R≤j≤i−L) \]

[i−R,i-L]
[i−R+1,i−L+1]
[i−R+2,i−L+2]
//套两个模板就可以了

//DP , 单调队列优化

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define frep(i, a, n) for (int i = a; i >= n; i--)
using namespace std;
const int N=1e7;
int a[N];
int f[N];
int que[N];
int h=0;
int t=0;
const int INF = 2e9;
int ans = -INF;
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int n,l,r;
    cin>>n>>l>>r;
    memset(f, 128, sizeof(f));
    f[0]=0;
    rep(i,0,n)
    {
        cin>>a[i];
    }
    rep(i,l,n)
    {
        while (que[h] + r < i && t >= h)
        {
            h++;
        }
        while(f[i-l]>f[que[t]]&&t>=h)
        {
            t--;
        }
        que[++t]=i-l;
        f[i]=f[que[h]]+a[i];
        if(i+r>n)
        {
            ans=max(ans,f[i]);
        }
    }
cout<<ans;
}

测试点编号	\(n=\)
\(1 \sim 3\)	\(10\)
\(4 \sim 6\)	\(500\)
\(7 \sim 10\)	\(2000\)
\(11 \sim 17\)	\(10^4\)
\(18 \sim 20\)	\(10^5\)

测试点	\(n \le\)	\(Q \le\)	特殊性质
\(1 \sim 4\)	\(10\)	\(10\)	无
\(5 \sim 9\)	\(300\)	\(300\)	无
\(10 \sim 13\)	\(1500\)	\(1500\)	无
\(14 \sim 16\)	\(8000\)	\(8000\)	保证所有输入的 \(a_i,v\) 互不相同
\(17 \sim 19\)	\(8000\)	\(8000\)	无
\(20 \sim 22\)	\(8000\)	\(2 \times 10^5\)	保证所有输入的 \(a_i,v\) 互不相同
\(23 \sim 25\)	\(8000\)	\(2 \times 10^5\)	无