并查集

并查集：(union-find sets)是一种简单的用途广泛的集合. 并查集是若干个不相交集合，能够实现较快的合并和判断元素所在集合的操作。

并查集的两种基本操作：

  • （1）合并；

  • （2）查询；

    初始化：

    1
    2
    3
    初始化： 每一个结点的上级都是自己，也就是说独立成一个集合 合并集合操作：
        for(i=1;i<=n;i++)
            f[i]=i;

    合并：

    1
    f[find(p2)]=find(p3);

    查询：

    1
    2
    3
    4
    int find(int k){
        if(f[k]==k)return k;
        return f[k]=find(f[k]);
    }

    总代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<bits/stdc++.h>
using namespace std;
int i,j,k,n,m,s,ans,f[10010],p1,p2,p3;
//f[i]表示i的集合名
int find(int k){
    if(f[k]==k)return k;
    return f[k]=find(f[k]);
}
int main()
{
    cin>>n>>m;
    for(i=1;i<=n;i++)
        f[i]=i;//初始化i的老大为自己
    for(i=1;i<=m;i++){
        cin>>p1>>p2>>p3;
        if(p1==1)
            f[find(p2)]=find(p3);
        else
            if(find(p2)==find(p3))
                printf("Y\n");
            else
                printf("N\n");
    }
    return 0;
}

扩展域并查集

拓展域并查集解决了一种多个有相互关系的并查集，放在一起考虑的问题。一般的并查集应用一般就是判断在不在一个集合，拓展域并查集讲的是多个集合，之间有相互关系一般为相互排斥关系，判断是否在一个集合等。

背景：

并查集能维护连通性、传递性，通俗地说，亲戚的亲戚是亲戚。

然而当我们需要维护一些对立关系，比如 敌人的敌人是朋友 时，正常的并查集就很难满足我们的需求。

这时，扩展域并查集就诞生了。

常见的做法是将原并查集扩大一倍规模，并划分为两个种类。

在同个种类的并查集中合并，和原始的并查集没什么区别，仍然表达他们是朋友这个含义。

考虑在不同种类的并查集中合并的意义，其实就表达 他们是敌人 这个含义了。

按照并查集美妙的 传递性，我们就能具体知道某两个元素到底是 敌人 还是 朋友 了。

具体实现，详见 P1525 关押罪犯。

[NOIP2010 提高组] 关押罪犯

题目背景

NOIP2010 提高组 T3

题目描述

S 城现有两座监狱，一共关押着 \(N\) 名罪犯，编号分别为 \(1\sim N\)。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久，如果客观条件具备则随时可能爆发冲突。我们用“怨气值”（一个正整数值）来表示某两名罪犯之间的仇恨程度，怨气值越大，则这两名罪犯之间的积怨越多。如果两名怨气值为 \(c\) 的罪犯被关押在同一监狱，他们俩之间会发生摩擦，并造成影响力为 \(c\) 的冲突事件。

每年年末，警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表，然后上报到 S 城 Z 市长那里。公务繁忙的 Z 市长只会去看列表中的第一个事件的影响力，如果影响很坏，他就会考虑撤换警察局长。

在详细考察了 \(N\) 名罪犯间的矛盾关系后，警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配，以求产生的冲突事件影响力都较小，从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨，那么他们一定会在每年的某个时候发生摩擦。

那么，应如何分配罪犯，才能使 Z 市长看到的那个冲突事件的影响力最小？这个最小值是多少？

输入格式

每行中两个数之间用一个空格隔开。第一行为两个正整数 \(N,M\)，分别表示罪犯的数目以及存在仇恨的罪犯对数。接下来的 \(M\) 行每行为三个正整数 \(a_j,b_j,c_j\)，表示 \(a_j\) 号和 \(b_j\) 号罪犯之间存在仇恨，其怨气值为 \(c_j\)。数据保证 \(1<a_j\leq b_j\leq N, 0 < c_j\leq 10^9\)，且每对罪犯组合只出现一次。

输出格式

共一行，为 Z 市长看到的那个冲突事件的影响力。如果本年内监狱中未发生任何冲突事件，请输出 0。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
4 6
1 4 2534
2 3 3512
1 2 28351
1 3 6618
2 4 1805
3 4 12884

样例输出 #1

1
3512

提示

输入输出样例说明

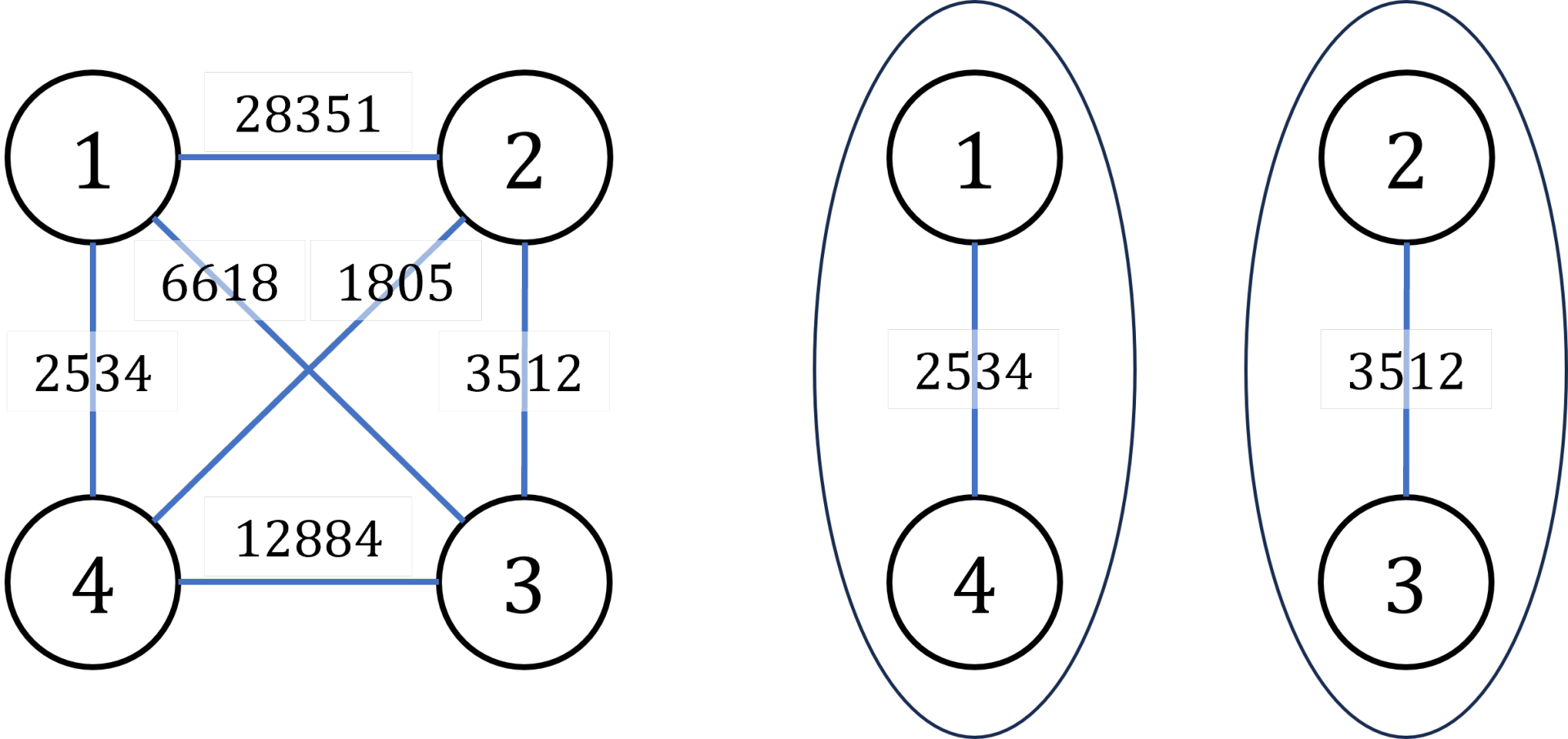
罪犯之间的怨气值如下面左图所示，右图所示为罪犯的分配方法，市长看到的冲突事件影响力是 \(3512\)（由 \(2\) 号和 \(3\) 号罪犯引发）。其他任何分法都不会比这个分法更优。

数据范围

对于 \(30\%\) 的数据有 \(N\leq 15\)。

对于 \(70\%\) 的数据有 \(N\leq 2000,M\leq 50000\)。

对于 \(100\%\) 的数据有 \(N\leq 20000,M\leq 100000\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<bits/stdc++.h>
using namespace std;
int n,m,f[40001],x,y;
struct _data
{
    int a,b,c;
} e[100001];
int gz( _data x,_data y)
{
    if(x.c>y.c)return 1;
    else return 0;
}
//我们要尽可能让危害大的罪犯在两个监狱里。
int find(int x)
{
    return f[x]==x?x:f[x]=find(f[x]);
}
int main()
{
  cin>>n>>m;
    for(int i=1; i<=m; i++)
      cin>>e[i].a>>e[i].b>>e[i].c;
    for(int i=1; i<=n*2; i++)
        f[i]=i;
    //初始化
    sort(e+1,e+m+1,gz);
    //排序
    for(int i=1; i<=m; i++)
    {
        x=find(e[i].a);
        y=find(e[i].b);
        //两个敌人还是相遇了，由于满足排序，因此可以
        if(x==y)
        {
          cout<<e[i].c<<'\n';
            return 0;
        }
        f[y] = find(e[i].a + n);
        //本人和敌人的敌人放一间
        f[x] = find(e[i].b + n);
        //本人和敌人的敌人放一间
    }
 cout<<0;
 }

　优点在于：结构简单，并查集的操作也不需要做改变，非常易于理解。　　缺点显然就是：需要额外存储空间。

[NOI2001] 食物链

题目描述

动物王国中有三类动物 \(A,B,C\)，这三类动物的食物链构成了有趣的环形。\(A\) 吃 \(B\)，\(B\) 吃 \(C\)，\(C\) 吃 \(A\)。

现有 \(N\) 个动物，以 \(1 \sim N\) 编号。每个动物都是 \(A,B,C\) 中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这 \(N\) 个动物所构成的食物链关系进行描述：

  • 第一种说法是 1 X Y，表示 \(X\) 和 \(Y\) 是同类。
  • 第二种说法是2 X Y，表示 \(X\) 吃 \(Y\)。

此人对 \(N\) 个动物，用上述两种说法，一句接一句地说出 \(K\) 句话，这 \(K\) 句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

  • 当前的话与前面的某些真的话冲突，就是假话；
  • 当前的话中 \(X\) 或 \(Y\) 比 \(N\) 大，就是假话；
  • 当前的话表示 \(X\) 吃 \(X\)，就是假话。

你的任务是根据给定的 \(N\) 和 \(K\) 句话，输出假话的总数。

输入格式

第一行两个整数，\(N,K\)，表示有 \(N\) 个动物，\(K\) 句话。

第二行开始每行一句话（按照题目要求，见样例）

输出格式

一行，一个整数，表示假话的总数。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5

样例输出 #1

1
3

提示

对于全部数据，\(1\le N\le 5 \times 10^4\)，\(1\le K \le 10^5\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for(int i=a;i<=n;i++)
const int N=5e6;
using ll=long long;
int n,k;
int f[N];
int find(int x)
{
	if(x==f[x])
	{
		return x;
	}
return f[x]=find(f[x]);
}
void union1(int x,int y)
{
f[find(x)]=find(y);
}
bool  issame(int x,int y)
{
	return find(x)==find(y);
}
int ans=0;
int main()
{
cin>>n>>k;
	rep(i,1,3*n)
	{
		f[i]=i;
	}
rep(i,1,k)
{
int a,b,c;
cin>>a>>b>>c;
if(b<=n&&c<=n)
{
if(a==1)
{
	//意味着二者关系相同
	if(!issame(b,c+n)&&!issame(b,c+2*n))
	{
        union1(b,c);
		union1(b+n,c+n);
		union1(b+2*n,c+2*n);
	}
	else
	{
		ans++;
	}
}
else
{
	if(b!=c)
	{
	if(!issame(b,c)&&!issame(b,c+n))
	{
		union1(b+n,c);
		union1(b+2*n,c+n);
		union1(b,c+2*n);
	}
	else
	{
		ans++;
	}		
	}
	else
	{
		ans++;
	}
}
}
    
else
{
	ans++;//超出范围
}
}
cout<<ans;
}

带权并查集

基本概念

带权并查集即是结点存有权值信息的并查集；当两个元素之间的关系可以量化，并且关系可以合并时，可以使用带权并查集来维护元素之间的关系；带权并查集每个元素的权通常描述其与并查集中祖先的关系，这种关系如何合并，路径压缩时就如何压缩；带权并查集可以推算集合内点的关系，而一般并查集只能判断属于某个集合。

如上文的食物链问题

这个题目需要维护推算集合内部的关系，所以可以利用带权并查集解决。

创建利用pre数组和rela数组判断集合关系，pre判断集合之间的关系，rela判断集合内部元素的关系，这题我们可以建立三种关系同类，捕食，和被捕食三种关系，我们在rela数组中分别用0，1，2表示：

  1. 0表示和根节点是同类关系
  2. 1表示和跟节点是捕食关系(吃根节点)
  3. 2表示和根节点是被捕食关系(被根节点吃)

首先是合并考虑压缩路径时的关系维护，我们压缩路径时已知a和b的关系，以及a和a根节点的关系，需要推导出b和a根节点的关系，如图是我们橙色线是我们要推导出的关系，黑色线是以知关系。

img
结点A与根关系 结点B与A关系 B与根关系
0 0 0
0 1 1
0 2 2
1 0 1
1 1 2
1 2 0
2 0 2
2 1 0
2 2 1 
1
2
3
4
5
6
7
8
9
10
int Find(int x){   // 查找当前结点的根节点
    if(x == pre[x]) return x;
    else
    {       // 压缩路径
        int temp = pre[x];
        pre[x] = Find(pre[x]); // 递归寻找头根点,压缩路径节点
        rela[x] = (rela[x] + rela[temp]) % 3; // 压缩路径关系
    }
   return pre[x];
}

然后我们考虑关系的查找，我们以及知道A和B在同一集合，即代表他们根节点相同，我们要确定两者之间的关系，我们还是线画出关系图，橙色线是我们要推导出的关系，黑色线是以知关系。

img
结点A与根关系 结点B与根关系 A与B关系
0 0 0
0 1 2
0 2 1
1 0 1
1 1 0
1 2 2
2 0 2
2 1 1
2 2 0 
1
2
3
4
if(Find(x) == Find(y)){ // 如果两个根节点相同
        relation = (rela[x] - rela[y] + 3) % 3; // 推出两个根节点之间的关系
       return relation == r; // 判断给出关系是否与已经存在的关系矛盾
}

最后我们考虑合并两个节点时关系的维护，我们已经知a和其根节点的关系，以及b和其根节点的关系，当我们把b集合合并到a集合时，我们需要考虑b根节点和a根节点存在的关系，关系图如下，橙色线是我们要推导出的关系，黑色线是以知关系。

img
结点A与根关系 结点B与根关系 结点B与A的关系 B根节点和A根节点的关系
0 0 0 0
0 0 1 1
0 0 2 2
0 1 0 2
0 1 1 0
0 1 2 1
0 2 0 1
0 2 1 2
0 2 2 0 
1
2
3
4
5
6
7
8
9
void Merge(int x, int y, int r){ // 合并两个节点关系
    int fx = Find(x);  // 查找 x,y的根节点
    int fy = Find(y);

    if(fx != fy){  //如根节点不同进行合并
        pre[fx] = fy;   //把x节点集合合并到y
        rela[fx] = (rela[y] - rela[x] + r + 3) % 3; //计算x头节点与y头节点的关系
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
//总代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 5e5 + 7;
int pre[maxn],rela[maxn];
int n, k, ans;
void init() // 初始化
{
    for(int i = 1; i <= n; i++){
         pre[i] = i; // 头节点等于自己本身
         rela[i] = 0; // 自己和自己肯定是同类
     }
    ans = 0; //记录假话数量
 }
 int Find(int x){   // 查找当前结点的根节点
     if(x == pre[x]) return x;
    else{       // 压缩路径
        int temp = pre[x];
         pre[x] = Find(pre[x]); // 递归寻找根节点,压缩路径节点
        rela[x] = (rela[x] + rela[temp]) % 3; // 压缩路径关系
    }
     return pre[x];
 } 
void Merge(int x, int y, int r){ // 合并两个节点关系
    int fx = Find(x);  // 查找 x,y的根节点
     int fy = Find(y);
 
     if(fx != fy){  //如根节点不同进行合并
         pre[fx] = fy;   //把x节点集合合并到y
         rela[fx] = (rela[y] - rela[x] + r + 3) % 3; //计算x头节点与y头节点的关系
     }
 }
 bool solve(int x,int y,int r){ // 判断真话假话
     int relation;
     if(x > n||y > n||(r == 1&&x == y))
     { // 根据题意直接判断的假话
             return false;
     }
     if(Find(x) == Find(y))
     { // 如果两个根节点相同
         relation = (rela[x] - rela[y] + 3) % 3; // 推出两个根节点之间的关系
        return relation == r; // 判断给出关系是否与已经存在的关系矛盾
     }
     else
         return true; //否则为真
  }
  /// 0 表示与根节点是同类
  /// 1 表示与根节点是捕食关系
 /// 2 表示与根节点是被捕食关系
  int main()
 {
	cin>>n>>k;
	init();
    int c, x, y;
     while(k--){
       cin>>c>>x>>y;
         c --;
         if(solve(x,y,c)){
             Merge(x,y,c); //真话合并两个节点关系
         }
         else
         {
             ans++; //假话答案自增
         }
     }
cout<<ans<<'\n';
    return 0;
 }