并查集训练

[NOI2015] 程序自动分析

题目描述

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设 \(x_1,x_2,x_3,\cdots\) 代表程序中出现的变量，给定 \(n\) 个形如 \(x_i=x_j\) 或 \(x_i\neq x_j\) 的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：\(x_1=x_2,x_2=x_3,x_3=x_4,x_4\neq x_1\)，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

输入格式

输入的第一行包含一个正整数 \(t\)，表示需要判定的问题个数。注意这些问题之间是相互独立的。

对于每个问题，包含若干行：

第一行包含一个正整数 \(n\)，表示该问题中需要被满足的约束条件个数。接下来 \(n\) 行，每行包括三个整数 \(i,j,e\)，描述一个相等/不等的约束条件，相邻整数之间用单个空格隔开。若 \(e=1\)，则该约束条件为 \(x_i=x_j\)。若\(e=0\)，则该约束条件为 \(x_i\neq x_j\)。

输出格式

输出包括 \(t\) 行。

输出文件的第 \(k\) 行输出一个字符串 YES 或者 NO（字母全部大写），YES 表示输入中的第 \(k\) 个问题判定为可以被满足，NO 表示不可被满足。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
2
2
1 2 1
1 2 0
2
1 2 1
2 1 1

样例输出 #1

1
2
NO
YES

样例 #2

样例输入 #2

1
2
3
4
5
6
7
8
9
10
2
3
1 2 1
2 3 1
3 1 1
4
1 2 1
2 3 1
3 4 1
1 4 0

样例输出 #2

1
2
YES
NO

提示

【样例解释1】

在第一个问题中，约束条件为：\(x_1=x_2,x_1\neq x_2\)。这两个约束条件互相矛盾，因此不可被同时满足。

在第二个问题中，约束条件为：\(x_1=x_2,x_1 = x_2\)。这两个约束条件是等价的，可以被同时满足。

【样例说明2】

在第一个问题中，约束条件有三个：\(x_1=x_2,x_2= x_3,x_3=x_1\)。只需赋值使得 \(x_1=x_2=x_3\)，即可同时满足所有的约束条件。

在第二个问题中，约束条件有四个：\(x_1=x_2,x_2= x_3,x_3=x_4,x_4\neq x_1\)。由前三个约束条件可以推出 \(x_1=x_2=x_3=x_4\)，然而最后一个约束条件却要求 \(x_1\neq x_4\)，因此不可被满足。

【数据范围】

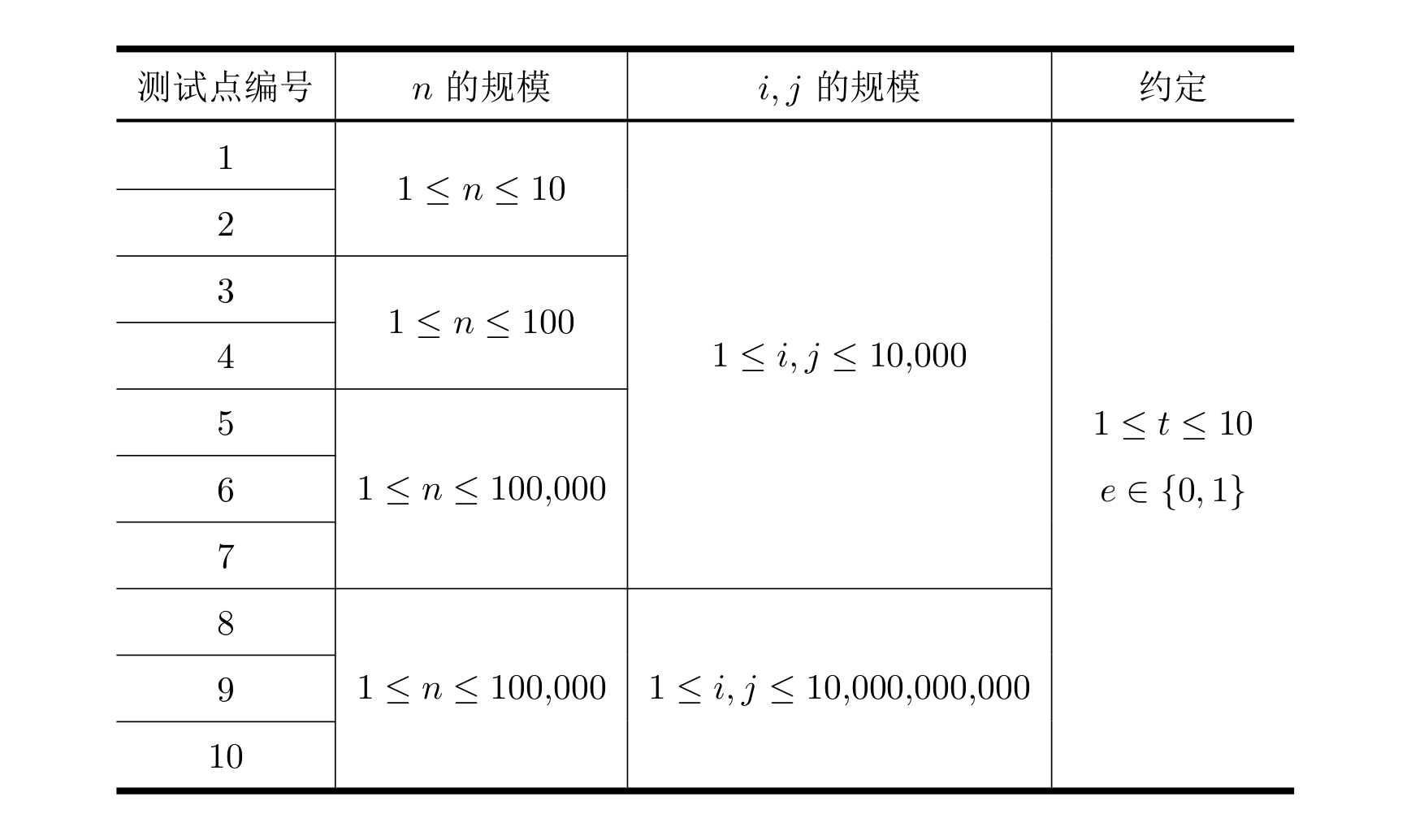
所有测试数据的范围和特点如下表所示：

勘误：测试点 \(8 \sim 10\) 的 \(i, j\) 约束为 \(1 \leq i, j \leq 10^9\)，而不是下图中的 \(10^{10}\)。

并查集+离散化

数据很大

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int fa[N];
int find(int x) {
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t;
    cin >> t;
    while (t--) {
        int n;
        cin >> n;
        iota(fa, fa + N, 0);
        vector<pair<int, int>> q[2];
        set<int> st;
        for (int i = 0; i < n; i++) {
            int x, y, z;
            cin >> x >> y >> z;
            q[z].emplace_back(x, y);
            st.insert(x);
            st.insert(y);
        }
        // 紧离散
        int idx = 0;
        unordered_map<int, int> mp;
        for (int x : st) mp[x] = ++idx;
        for (auto [x, y] : q[1]) 
        {
            int rx = find(mp[x]), ry = find(mp[y]);
            fa[rx] = ry;
        }
        bool ok = true;
        for (auto [x, y] : q[0]) 
        {
            int rx = find(mp[x]), ry = find(mp[y]);
            if (rx == ry) {
                ok = false;
                break;
            }
        }
        if (ok) cout << "YES" << endl;
        else cout << "NO" << endl;
    }
}

[NOI2002] 银河英雄传说

题目背景

公元 \(5801\) 年，地球居民迁至金牛座 \(\alpha\) 第二行星，在那里发表银河联邦创立宣言，同年改元为宇宙历元年，并开始向银河系深处拓展。

宇宙历 \(799\) 年，银河系的两大军事集团在巴米利恩星域爆发战争。泰山压顶集团派宇宙舰队司令莱因哈特率领十万余艘战舰出征，气吞山河集团点名将杨威利组织麾下三万艘战舰迎敌。

题目描述

杨威利擅长排兵布阵，巧妙运用各种战术屡次以少胜多，难免恣生骄气。在这次决战中，他将巴米利恩星域战场划分成 \(30000\) 列，每列依次编号为 \(1, 2,\ldots ,30000\)。之后，他把自己的战舰也依次编号为 \(1, 2, \ldots , 30000\)，让第 \(i\) 号战舰处于第 \(i\) 列，形成“一字长蛇阵”，诱敌深入。这是初始阵形。当进犯之敌到达时，杨威利会多次发布合并指令，将大部分战舰集中在某几列上，实施密集攻击。合并指令为 M i j，含义为第 \(i\) 号战舰所在的整个战舰队列，作为一个整体（头在前尾在后）接至第 \(j\) 号战舰所在的战舰队列的尾部。显然战舰队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增大。

然而，老谋深算的莱因哈特早已在战略上取得了主动。在交战中，他可以通过庞大的情报网络随时监听杨威利的舰队调动指令。

在杨威利发布指令调动舰队的同时，莱因哈特为了及时了解当前杨威利的战舰分布情况，也会发出一些询问指令：C i j。该指令意思是，询问电脑，杨威利的第 \(i\) 号战舰与第 \(j\) 号战舰当前是否在同一列中，如果在同一列中，那么它们之间布置有多少战舰。

作为一个资深的高级程序设计员，你被要求编写程序分析杨威利的指令，以及回答莱因哈特的询问。

输入格式

第一行有一个整数 \(T\)（\(1 \le T \le 5 \times 10^5\)），表示总共有 \(T\) 条指令。

以下有 \(T\) 行，每行有一条指令。指令有两种格式：

  1. M i j：\(i\) 和 \(j\) 是两个整数（\(1 \le i,j \le 30000\)），表示指令涉及的战舰编号。该指令是莱因哈特窃听到的杨威利发布的舰队调动指令，并且保证第 \(i\) 号战舰与第 \(j\) 号战舰不在同一列。

  2. C i j：\(i\) 和 \(j\) 是两个整数（\(1 \le i,j \le 30000\)），表示指令涉及的战舰编号。该指令是莱因哈特发布的询问指令。

输出格式

依次对输入的每一条指令进行分析和处理：

  • 如果是杨威利发布的舰队调动指令，则表示舰队排列发生了变化，你的程序要注意到这一点，但是不要输出任何信息。
  • 如果是莱因哈特发布的询问指令，你的程序要输出一行，仅包含一个整数，表示在同一列上，第 \(i\) 号战舰与第 \(j\) 号战舰之间布置的战舰数目。如果第 \(i\) 号战舰与第 \(j\) 号战舰当前不在同一列上，则输出 \(-1\)。

样例 #1

样例输入 #1

1
2
3
4
5
4
M 2 3
C 1 2
M 2 4
C 4 2

样例输出 #1

1
2
-1
1

提示

样例解释

战舰位置图：表格中阿拉伯数字表示战舰编号。

这题挺有趣的，或许可以更好的理解并查集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<bits/stdc++.h>
using namespace std;
const int N = 30010;
int n = 30000,m;
int p[N],d[N],s[N];
int find (int x) {
    if (p[x] != x) 
    {
        int rx = find (p[x]);
        d[x] += d[p[x]];
        //核心
        p[x] = rx;
    }
    return p[x];
}
int main () 
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> m;
    for (int i = 1;i <= n;i++) p[i] = i,s[i] = 1;
    while (m--) {
        char op;
        int a,b;
        cin >> op >> a >> b;
        int ra = find (a),rb = find (b);
        if (op == 'M') 
        {
            if (ra != rb) 
            {
                p[ra] = rb;
                //并查集归为一起
                d[ra] = s[rb];
                //在哪里直接加上
                s[rb] += s[ra];
                //下面接的部分变长了
            }
        }
        else {
            if (ra != rb) cout<<-1<<endl;
            else cout << max (0,abs (d[a] - d[b]) - 1) << endl;
            //输出差值
        } 
    }
    return 0;
}

[CEOI1999] Parity Game

题目描述

Alice 和 Bob 在玩一个游戏：他写一个由 \(0\) 和 \(1\) 组成的序列。Alice 选其中的一段（比如第 \(3\) 位到第 \(5\) 位），问他这段里面有奇数个 \(1\) 还是偶数个 \(1\)。Bob 回答你的问题，然后 Alice 继续问。Alice 要检查 Bob 的答案，指出在 Bob 的第几个回答一定有问题。有问题的意思就是存在一个 \(01\) 序列满足这个回答前的所有回答，而且不存在序列满足这个回答前的所有回答及这个回答。

输入格式

第 \(1\) 行一个整数 \(n\)，是这个 \(01\) 序列的长度。

第 \(2\) 行一个整数 \(m\)，是问题和答案的个数。

第 \(3\) 行开始是问题和答案，每行先有两个整数，表示你询问的段的开始位置和结束位置。然后是 Bob 的回答。odd表示有奇数个 \(1\)，even 表示有偶数个 \(1\)。

输出格式

输出一行，一个数 \(x\)，表示存在一个 \(01\) 序列满足第 \(1\) 到第 \(x\) 个回答，但是不存在序列满足第 \(1\) 到第 \(x+1\) 个回答。如果所有回答都没问题，你就输出所有回答的个数。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
10
5
1 2 even
3 4 odd
5 6 even
1 6 even
7 10 odd

样例输出 #1

1
3

提示

对于 \(100\%\) 的数据，\(1 \le n \leq 10^9\)，\(m \leq 5 \times 10^3\)。

种类并查集+离散化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include<iostream>
#include<algorithm>
using namespace std;
int n, m;
const int N = 1e6;
int fa[N];
//并查集
inline int find(int x) {
	if (fa[x] == x) return x;
	return fa[x] = find(fa[x]);
}
void merge(int x, int y)
{
	int dx = find(x);
	int dy = find(y);
	if (dx != dy)
	{
		fa[dx] = dy;
	}
}
struct shuzi
{
	int x, y, z;
}a[N];
int d[2*N];
int top;
int main()
{
	cin >> n >> m;
	string s;
	for (int i = 1; i <= m; i++)
	{
		cin >> a[i].x >> a[i].y;
		a[i].x--;
		d[++top] = a[i].x;
		d[++top] = a[i].y;
		cin >> s;
		if (s[0] == 'o')
		{
			a[i].z = 1;
		}
		//奇数
		else
		{
			a[i].z = 0;
		}
		//偶数
}
	sort(d + 1, d + 1 + top);
	int x = unique(d + 1, d + 1 + top) - d - 1;
	//记录去重后的长度
	for (int i = 1; i <= 2 * x; i++)
	{
		fa[i] = i;
		//并查集初始化
	}
	for (int i = 1; i <= m; i++)
	{
		a[i].x = lower_bound(d + 1, d + 1 + x, a[i].x) - d;
		a[i].y = lower_bound(d + 1, d + 1 +x, a[i].y) - d;
		if (a[i].z)
		{
			//奇数
			if (find(a[i].x) == find(a[i].y))
			{
				//如果两个数奇偶性相同
				cout << i - 1;
				return 0;
			}
			else
			{
				merge(a[i].x, a[i].y + x);
				merge(a[i].x + x, a[i].y);
			}
		}
		else
		{
			if (find(a[i].x) == find(a[i].y + x))
			{
				cout << i - 1;
				return 0;
			}
			else
			{
				merge(a[i].x, a[i].y );
				merge(a[i].x+x, a[i].y + x);
			}


		}
	}
	cout << m;
}

[NOI2001] 食物链

题目描述

动物王国中有三类动物 \(A,B,C\)，这三类动物的食物链构成了有趣的环形。\(A\) 吃 \(B\)，\(B\) 吃 \(C\)，\(C\) 吃 \(A\)。

现有 \(N\) 个动物，以 \(1 \sim N\) 编号。每个动物都是 \(A,B,C\) 中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这 \(N\) 个动物所构成的食物链关系进行描述：

  • 第一种说法是 1 X Y，表示 \(X\) 和 \(Y\) 是同类。
  • 第二种说法是2 X Y，表示 \(X\) 吃 \(Y\)。

此人对 \(N\) 个动物，用上述两种说法，一句接一句地说出 \(K\) 句话，这 \(K\) 句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

  • 当前的话与前面的某些真的话冲突，就是假话；
  • 当前的话中 \(X\) 或 \(Y\) 比 \(N\) 大，就是假话；
  • 当前的话表示 \(X\) 吃 \(X\)，就是假话。

你的任务是根据给定的 \(N\) 和 \(K\) 句话，输出假话的总数。

输入格式

第一行两个整数，\(N,K\)，表示有 \(N\) 个动物，\(K\) 句话。

第二行开始每行一句话（按照题目要求，见样例）

输出格式

一行，一个整数，表示假话的总数。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5

样例输出 #1

1
3

提示

对于全部数据，\(1\le N\le 5 \times 10^4\)，\(1\le K \le 10^5\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for(int i=a;i<=n;i++)
const int N=5e6;
using ll=long long;
int n,k;
int f[N];
int find(int x)
{
	if(x==f[x])
	{
		return x;
	}
return f[x]=find(f[x]);
}
void union1(int x,int y)
{
f[find(x)]=find(y);
}
bool  issame(int x,int y)
{
	return find(x)==find(y);
}
int ans=0;
int main()
{
cin>>n>>k;
	rep(i,1,3*n)
	{
		f[i]=i;
	}
rep(i,1,k)
{
int a,b,c;
cin>>a>>b>>c;
if(b<=n&&c<=n)
{
if(a==1)
{
	//意味着二者关系相同
	if(!issame(b,c+n)&&!issame(b,c+2*n))
	{
        union1(b,c);
		union1(b+n,c+n);
		union1(b+2*n,c+2*n);
	}
	else
	{
		ans++;
	}
}
else
{
	if(b!=c)
	{
	if(!issame(b,c)&&!issame(b,c+n))
	{
		union1(b+n,c);
		union1(b+2*n,c+n);
		union1(b,c+2*n);
	}
	else
	{
		ans++;
	}		
	}
	else
	{
		ans++;
	}

}
}
else
{
	ans++;
}
}
cout<<ans;
}