数字设计和计算机体系结构

第一章

知识一览：

关于数制

十进制数、二进制数、十六进制数的每一位的权不同。权是$a^n$，（n为该位数右边位数的个数，如最低位的n是0，a是模数，二进制数a为2，十进制10，十六进制16...）【书上是$a^(N-1)$,N为该位数所在位】

十进制转换为2进制，从高位到低位逐个求得，减去最接近的2的幂次方。从低位到高位逐个求得，先对2求余，得到最低位，再对商求余得到商的最低位，得到第2位，再对新商求余......整个过程可以理解为是对2求余，对4求余，对8求余，对16求余.......其实和从高到低求是一样的理解。

二进制转换为十进制、二进制和十六进制的相互转换很简单。

关于字节

8bit= 1 byte，word有32bit 64bit，等，所以1word = n byte = 8n bit

最低有效位，最低有效字节，最高有效位，最高有效字节。

二进制的原码、反码、补码

主要目的是为了解决负数的表示与计算。

正数的原码反码补码相同，负数的补码是反码+1。

取反可以理解是模数-绝对值-1。比如101取反是010，两者相加为7。

不考虑符号位，补码的数值位则是模数-绝对值。

补码的最高位的权是$-2^{(N-1)}$，其他位同无符号二进制数。所以考虑符号位，补码则表示模数-绝对值$-2^{(N-1)}$，$2^{(N-1)}$就是模数，所以补码表示的意思就是 -绝对值，那么就是一个负数了。

如此以来就可以理解减法的补码表示。例如正数A-B（N位有符号数），用补码表示则是$A+2^{（N-1）}-1-B+1=A-B+2^{（N-1）}$。如果A>B，那么计算后输出进位cout一定为1，如果A<B，输出进位cout一定为0.

对负数求补码时，有两种方法，1，对其绝对值正数所有位取反，+1，2，理解成$-2^{(N-1)}$+补数。

比如-7，理解是-8+1，那就是1001。也可以是0111取反1000，再+1。但是当位数多时，比如8位数表示-3，就不好用方法2了，用方法1方便很多。0000_0011再取反+1得1111_1101。

对负数的补码求其值时，有两种方法，1，所有位取反+1，得到绝对值；2，用各位权直接相加。

判断相加溢出的条件：相加两个数符号相同，且结果的符合与被加数相反。

无符号原码表示范围 [0,2^N-1];

有符号原码表示范围 [-2^(N-1)+1,2(N-1)-1];

二进制补码表示范围【-2^（N-1）,2(N-1)-1】

逻辑门的区分

非门、与门、或门、缓冲门、与非NAND、或非NOR、异或XOR、同或XNOR，多输入门。

数字抽象

电源电压 5V 3.3 2.5 1.8 1.5 1.2

逻辑电平与噪声容限注意VDD VOH VOL GND 以及 VIH VIL的作用

有效输出被有效接收，正确判别，需要满足VOH>VIH，VOL<VIL。

VIL-VOL，VOH-VIH为低、高电平噪声容限。

噪声容限是为了判断噪声电压是否会影响输出。

直流电压传输特性。

静态约束，逻辑电平兼容性。

TTL CMOS LVTTL LVCMOS 其中LV是LOW VOLTAGE的意思接触到时再查表。

逻辑门

非门

NOT 逻辑门具有一个输入和一个输出，其中输出是输入的补码。如果输入为 0（低），则非门的输出为 1（高），如果输入为 1（高），非门的输出为 0（低）。

由于非门的输出是输入的补码，因此也称为反相或补码电路（门）。

如果 A 是 NOT 门的输入，Y 是其输出，则 NOT 门的逻辑方程为 Y = 。

下面给出了非门的逻辑符号和真值表。

输入 (A)	输出（Y = A）
0	1
1	0

或门

或门是一个双输入逻辑门，可对其输入执行布尔或运算。仅当两个输入均为 0（低）时，或门的输出才为 0（低）。对于输入的所有其他组合，或门的输出为 1（高）。

如果 A 和 B 是 OR Gate 的输入，Y 是其输出，则 OR Gate 的逻辑表达式为 Y = A + B，读作“Y 等于 A OR B”。

OR门的逻辑符号和真值表如下所示。

输入 (A)	输入 (B)	输出（Y =A+B）
0	0	0
0	1	1
1	0	1
1	1	1

与门

与门是一个双输入逻辑门，可对其输入执行布尔与运算。与门的输出只有在其两个输入均为 1（高电平）时才为 1（高电平）。对于所有其他情况，与门的输出为 0（低）。

如果 A 和 B 是 AND 门的输入，Y 是其输出，则 AND 门的逻辑表达式为 Y = A ‧ B，读作“Y 等于 A AND B”。

与门的逻辑符号和真值表如下所示。

输入 (A)	输入 (B)	输出 (Y=A‧B)
0	0	0
0	1	0
1	0	0
1	1	1

异或门

异或门，通常写为异或门或异或门，是一个双输入逻辑门，对其输入执行异或运算。如果输入不同，即一个输入为 1（高）而另一个输入为 0（低），则异或门的输出为 1（高）。如果两个输入相同，即均为 1（HIGH）或均为 0（LOW），则 XOR Gate 的输出为 0（LOW）。

如果 A 和 B 是 XOR Gate 的输入，Y 是其输出，则 XOR 门的逻辑表达式为 Y = A B + A B 或 Y = A ⊕ B。

异或门的逻辑符号和真值表如下所示。

输入 (A)	输入 (B)	输出（Y=A⊕B）
0	0	0
0	1	1
1	0	1
1	1	0

缓冲

缓冲器是一个有趣的电路，它不做任何逻辑运算，而是充当信号放大器。缓冲区的输出与输入相同，它充当传递函数。

通常，缓冲器可用作三态缓冲器，它有一个额外的“启用”输入。当Enable (E) 输入为0 (LOW) 时，输出处于高阻状态，当Enable (E) 输入为1 (HIGH) 时，输出跟随输入，即与输入相同。

在内部，缓冲器被配置为两个背靠背连接的非门。

缓冲器的逻辑符号和真值表如下所示。

输入 (A)	输出（Y=A）
0	0
1	1

与非门

接下来的两个门被称为通用门。其中，第一个是与非门。它代表非与门，即一个与门后跟一个非门。与非的输出是与门的补码，即只有当两个输入均为 1（高）时，与非门的输出才为 0（低）。在所有其他情况下，其输出为 1（高）。

如果 A 和 B 是 NAND 门的输入，Y 是其输出，则 NAND 门的逻辑表达式为 Y = A ‧ B。

NAND门的逻辑符号和真值表如下所示。

输入 (A)	输入 (B)	输出 (Y= A ‧ B )
0	0	1
0	1	1
1	0	1
1	1	0

或非门

就像 AND 有 NAND，OR 门有 NOR 门。它代表非或门，正如预期的那样，它是一个或门，后跟一个非门。当且仅当其两个输入均为 0（低）时，或非门的输出为 1（高）。在所有其他输入组合中，或非门的输出为 0（低）。

如果 A 和 B 是 NOR Gate 的输入，Y 是它的输出，那么 NOR Gate 的逻辑表达式是 Y= A + B。

或非门的逻辑符号和真值表如下所示。

输入 (A)	输入 (B)	输出（Y= A + B）
0	0	1
0	1	0
1	0	0
1	1	0

异或门

最后一个重要的逻辑门是异或门。它通常写为 EX-NOR 或 XNOR Gate。它相当于一个 XOR 门后跟一个 NOT 门。如果 XNOR Gate 的两个输入相同，即两个输入均为 0（LOW）或 1（HIGH），则 XNOR Gate 的输出为 1（HIGH）。如果 XNOR Gate 的输入不同，则其输出为 0 (LOW)。

如果 A 和 B 是 XNOR Gate 的输入，Y 是它的输出，那么 XNOR Gate 的逻辑表达式是 Y = A ⊕ B。

或非门的逻辑符号和真值表如下所示。

输入 (A)	输入 (B)	输出 (Y= A ⊕ B )
0	0	1
0	1	0
1	0	0
1	1	1

多输入门没什么区别，牢记上述即可。

数字抽象之下

逻辑电平，将连续变量映射到离散的二进制变量

第一个门称为驱动源

第二个门称为接收端

驱动源的输出连接到接收端的输入

电压处在0-$V_{OL}$之间的画驱动源产生LOW（0）输出

否则产生High(1)输出

电压位于$V_{OH}$-$V_{DD}$之间

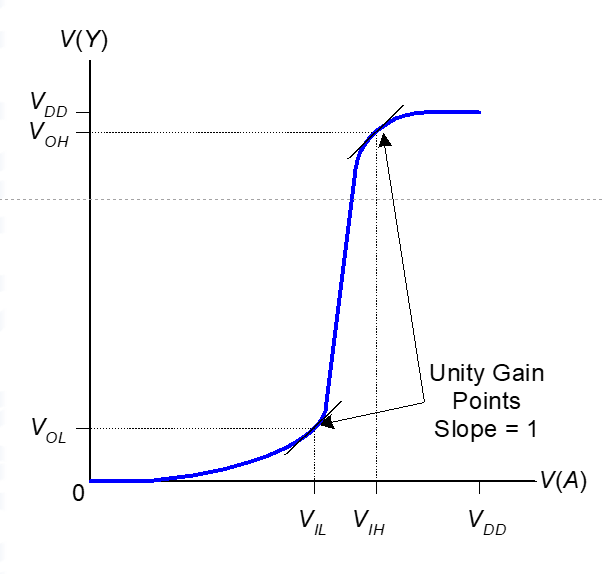
OH和OL称之为输出高和输出低逻辑电平

如果是0-$V_{IL}$之间就是low，$V_{IH}-V_{DD}$就是HIgh

如果接收端处于$V_{IL}-V_{IH}$之间就是禁止区域，无法预测

IH和IL称之为输入高和输入低电平 NMH = VOH – VIH NML = VIL – VOL

习题计算：

第二章

组合逻辑设计

Introduction Boolean Equations Boolean Algebra From Logic to Gates Multilevel Combinational Logic X’s and Z’s, Oh My Karnaugh Maps Combinational Building Blocks Timing

组合电路和时序电路的区别是在于输出是否与之前的状态有关。本章还介绍了布尔表达式，布尔代数等知识点，推气泡法是比较好的能根据电路原理图快速写出逻辑电路的表达式的方法。

然后是卡诺图化简方法。数据选择器、译码电路等。

时序概念与毛刺

数字电路可以分为组合（combinational）电路和时序（sequential）电路。组合电路的输出仅仅取决于输入的值，换句话说，它组合当前输入值来确定输出的值。举个例子，一个逻辑门是一个组合电路。时序电路的输出取决于当前输入值和之前的输入值，换句话说，它取决于输入的序列。组合电路是没有记忆的，但是时序电路是有记忆的。这一章重点放在组合电路上，第3章考察时序电路。

组合逻辑电路：

电路任意时刻的输出仅仅取决于该时刻的输入，与电路原来的状态无关。（没有储存功能）

组合逻辑电路的构成：

连接多个电路元件的电路是组合电路的条件；
每个电路元件本身就是组合电路;
每个电路的结点或者是一个电路的输入，或者是连接到外部电路的一个输出端;
电路不包含回路;

A logic circuit is composed of: Inputs Outputs Functional specification功能规范 Timing specification时序规范

总线： 总线是一组属性相同的多根信号线，比如多根数据线，多根地址线。画图时，用一根线表示多个信号线，总线上有一个斜线，并在旁边标注了信号线数量的数字。

在满足以下条件时，它就是组合电路。

每一个电路元件本身都是组合电路；
每一个电路节点或者是一个电路的输入，或者是连接外部电路的一个输出端；
电路不能包含回路：经过电路的每条路径最多只能经过每个电路节点一次。

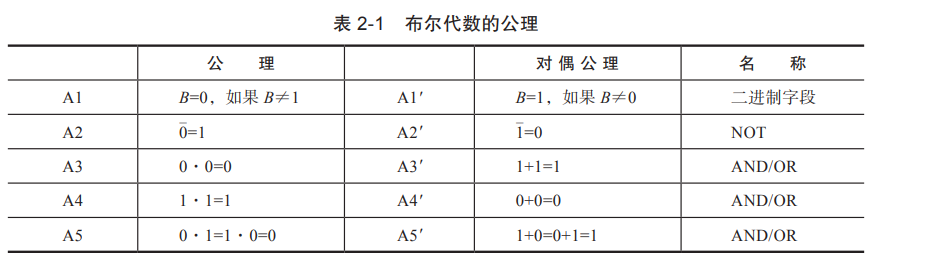
布尔代数处理二进制（布尔）变量和逻辑

布尔代数又称为逻辑代数，开关代数，是一个由逻辑变量真假（或取值1，0 ）、以及用“与”、“或”、“非”3种基本运算构成的代数系统。
布尔代数中的1和0是逻辑常量，它们不具备数的性质，无大、小、正、负之分，仅仅表示真、假两个相反的逻辑状态；

几个术语集合：项：原变量或它的反变量，如A，$A \overline{A}$ 乘积项（与项）：一个项或多个项的与，如AB,$A $

最小项：对于n个输入变量，若m为包含n个变量的与项，且这n个变量均以原变量或反变量的形式在m中只出现一次；则称m为该组变量的最小项。n变量的最小项有$2^n$个。

如AB, $A\overline{B}$ ,都是输入为A,B两个变量的最小项。 (sum of products)SOP

求和是1的然后与起来最后或起来。

求和项（或项）：一个项或者多个项的或，如A+$B\overline{B}$ +C; 最大项：对于n个输入变量，若M为包含n个变量的或项，且这n个变量均以原变量或反变量的形式在M中只出现一次；则称M为该组变量的最大项。 n变量的最大项有$2^n$个。如A+$\overline{B}$ 是输入为A,B两个变量的最大项。 (product of sum)POS

与或式：由与项之和构成的逻辑表达式，

例题：

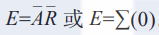
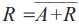
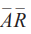
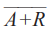
Ben正在野炊，如果天气下雨或者那儿有蚂蚁，Ben将不能享受到野炊的快乐。设计一个电路，当其输出为真时表示Ben可以享受野炊。解：首先定义输入和输出。输入为A和R，它们分别表示有蚂蚁和下雨，有蚂蚁时A是真，没有蚂蚁时A为假。同样，下雨时R为真，不下雨时R为假。输出为E，表示Ben可以享受野炊。如果Ben享受野炊，E为真，如果Ben没能去野炊，E为假。图2-10表示Ben野炊经历的真值表。使用与或式，我们写出的等式如下：。可以用2个反向器和2个与门来实现等式，如图2-11a所示。读者可能发现这个真值表是1.5.5节中出现的或非函数：E=A NOR。图2-11b表示或非操作。在2.3节中，我们将介绍和这两个等式是等价的。

对具有任何多变量的真值表可以用与或式写出唯一的布尔表达式。

或与式：由或项之与构成的逻辑表达式.

真值表中有2个行输出为假，所以函数可以写成或与式：Y=(A+B)(A+B)。

总结：

与或式就是找到为1的式子然后或起来，

或与式就是找到为0的式子然后与起来。

逻辑函数式（逻辑表达式）：

将输出与输入之间的逻辑关系写成与、或、非的运算组合形式。

逻辑图：

用图形符号表示逻辑函数中的与、或、非等关系。

一堆公理：

单变量定理

表2-2中的定理T1到T5描述了如何化简包含一个变量的等式。

如何化简包含多个变量的布尔表达式。

推气泡的规则：

向后推输出端的气泡或者向前推输入端的气泡，需要将与门换成或门，反之亦然；
从输出端推气泡返回到输入端，把气泡放置在门的输入端；
在所有门的输入端向前推气泡，把气泡放置在门的输出端。

我的想法是直接把一个门前面有圆形的给推回去即可，就尽量不要让圆形在前面。

学会一下等式化简

电路原理图

通常遵循以下准则：

输入在原理图的左边或者顶部；
输出在原理图的右边或者底部；
无论何时，门必须从左至右流；
最好使用直线而不是有很多拐角的线（交错的线需要浪费精力考虑如何走线）；
走线总是在T交叉点连接；
在两条线交叉的地方有一个点，表示它们之间有连接；
在两条线交叉的地方没有点，表示它们没有连接。

有一种优先级电路：

硬件的简化：

X和Z

布尔代数被限制为0和1。然而，真实的电路中会出现非法值和浮空现象，分别用X和Z来表示。（Floating, high impedance, open, high Z Floating output might be 0, 1, or somewhere in between）

非法值X

符号X表示电路节点的值未知（unknown）或非法（illegal），通常发生在此节点同时被0和1驱动的情况下。

浮空Z

符号Z表示节点既没有被高电平驱动也没有被低电平驱动。这个节点被称为浮空（floa-ting）、高阻态（high impedance）或者高Z态。一个典型的误解是将浮空或未被驱动的节点和逻辑0等同。事实上，这个浮空的节点可能是0也可能是1，也有可能是在0和1之间的电压。这取决于系统先前的状态。一个浮空节点并不意味着电路出错，一旦有其他电路元件将这个节点驱动到有效电平，这个节点上的值就可以参与电路操作。

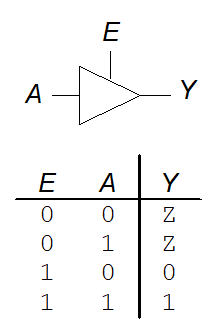
图2-40所示的三态缓冲器（tristate buffer）有3种可能输出：高电平（1）、低电平（0）和浮空（Z）。三态缓冲器有输入端A、输出端Y和使能端E。当使能端为真时，三态缓冲器作为一个简单的缓冲器，传送输入值到输出端。当使能端为假的时候，输出被置为高阻态（Z）。

需要知道一下三态缓冲器

卡诺图：

其实核心就是三个：一个是尽量多的包含，一个是注意边边角角，一个就是注意是00,01,10,11的顺序

7段数码管显示译码器。

无关项

2.4节中介绍了真值表无关项。当一些变量对输出没有影响时可以减少表中行的数量。无关项表示成符号X，它的意思是输入可能是0或者1。当输出的值不重要或者相对应的输入组合从不出现时，无关项也会出现在真值表的输出中。由设计师决定这些输出是0还是1。

带有无关项的7段数码管显示译码器。不考虑非法输入值10～15产生的输出

这个地方核心是把x看成1

多路选择器

根据选择（select）信号的值从几个可能的输入中选择一个作为输出。多路选择器有时简称为mux。

如果S=0，Y=D0；如果S=1，Y=D1。S也称为控制信号（control signal），因为它控制多路选择器如何操作。

更宽的多路选择器

也可以：

更好的理解？

用多路选择器实现逻辑

用多路选择器实现逻辑。Alyssa需要实现函数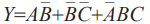完成她的毕业设计。但是，当她查看实验工具箱时，发现只剩下一个8:1多路选择器。她如何实现这个函数？

上面这种很简单粗暴了其实。

再次用多路选择器实现逻辑。在期末报告前，Alyssa打开电路的电源，结果将8:1多路选择器烧坏了（由于前一天整晚没有休息，她意外地用20V电压代替5V电压供电）。她请求她的朋友将余下的元器件给她。他们给了她一个4:1多路选择器和一个非门。她如何只用这些部件构造新电路？解：通过让输出取决于C的值，Alyssa将真值表减少到4行。（她也尝试过重新排列真值表的列，使输出取决于A或B的取值。）图2-62给出了新的设计。

译码器

译码器有N个输入和$2^N$个输出。它的每一个输出都取决于输入的组合。图2-63给出了一个2:4译码器。当A1:0=00时Y0=1，当A1:0=01时Y1=1，等等。输出称为独热（one-hot）状态，因为在给定的条件下恰好只有一个输出为高电平。

时序

传输延迟和最小延迟

组合逻辑电路的时序特征包括传输延迟（propagation delay）和最小延迟（contamination delay）。传输延迟tpd是输入改变直到对应的一个或多个输出达到最终的值所经历的最长时间。最小延迟tcd是一个输入发生变化到任何一个输出开始改变的最短时间。

弧形表示在A发生转变tcd时间后Y开始改变，在tpd时间后Y的新值稳定下来。

关键路径（critical path）是从A或者B到输出Y。因为输入通过了3个门才传输到输出，所以它是最长的一条路径，也是最慢的路径。这个路径成为关键路径，是因为它限制了电路运行的速度。最短路径（short path）是从输入D到输出Y。因为从输入通过1个门就到输出，所以此路径是最短的路径，也是通过电路的最快路径。

组合电路的传输延迟是关键路径上每一个元件的传输延迟之和。最小延迟是最短路径上每个元件的最小延迟之和。这些延迟如图2-69所示，也可由下列等式描述：

延迟计算

毛刺

一个输入信号的改变可能会导致多个输出信号的改变。这被称为毛刺（glitch）或者冒险（hazard）

当A=0，C=1，B从1变成0时最短的路径（用浅灰色显示）通过与门和或门两个门。关键路径（用深灰色显示）通过一个反相器以及与门和或门两个门。当B从1变成0，n2（在最短路径上）在n1（在关键路径上）上升之前下降。直到n1上升前，两个输入到或门都是0，输出Y下降到0。当n1最后上升后，Y的值回到1。时序图如图2-76所示，Y的值从1开始，结束时也为1，但是存在暂时为0的毛刺。

只要读取输出之前的等待时间和传输延迟一样长，出现毛刺就不会有问题，这是因为输出最终将稳定在正确的值。

避免毛刺需要多加硬件。

第3章

Introduction Latches and Flip-Flops 锁存器和触发器 Synchronous Logic Design 同步逻辑设计 Finite State Machines 有限状态机 Timing of Sequential Logic 时序逻辑电路的时序 Parallelism并行

时序逻辑设计

反相器交叉耦合（cross-coupled），稳态。 Bistable circuit双稳态电路/元件

交叉耦合的反相器有两种稳定状态：Q=0和Q=1，所以电路被称为双稳态。

双稳态元件可以存储一位信息，没有用于控制状态的输入，所以它并没有什么实用价值。

SR Latch SR锁存器

假设Q的初值已知，记为Qprev。在我们进入情况Ⅳ之前，Qprev为1或者为0表示系统状态。当R=S=0时，Q将保持初值Qprev不变，Q将取Q初值的反值（Qprev）。这个电路有记忆功能。

输入S和R表示置位和复位。置位表示将一个位设为1，复位表示将一个位设为0。

R和S同时有效是没有意义的，因为锁存器不可能同时被置位或者复位，这样会产生两个输出为0的混乱电路响应。

D Latch D锁存器

为什么会出现这个东西哦，因为SR锁存器中S和R同时取真值时候，其输出不确定。

D锁存器解决了这些问题。它有2个输入：数据输入D用以控制下一个状态的值；时钟输入CLK用以控制状态发生改变的时间。

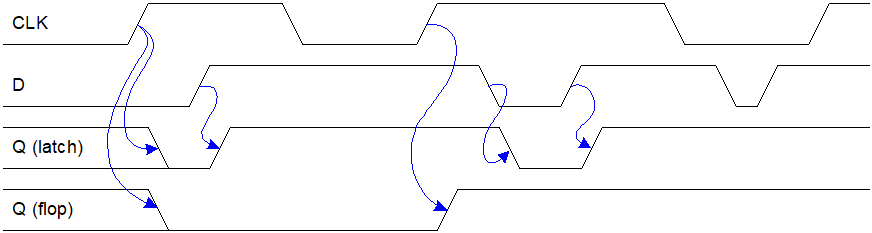
当CLK=1时，D锁存器是透明的（trans-parent）：数据D通过D锁存器流向Q，D锁存器就像是一个缓冲器。当CLK=0时，D锁存器是阻塞的（opaque）：它阻止了新的数据D通过D锁存器流向Q，Q保持原来的值不变。所以D锁存器有时被称为透明锁存器或者电平敏感锁存器。

D Flip-flop D触发器

锁存器L1称为主锁存器。第二个锁存器L2称为从锁存器。它们之间的节点为N1。

当CLK=0时主锁存器是透明的，从锁存器是阻塞的。所以D的值将无条件传送到N1。

当CLK=1时，主锁存器变成阻塞的，从锁存器变成透明的。N1的值将传送到Q，但是N1和D之间被切断。

在时钟从0上升到1之前并且在时钟开始上升之后，D值立即被复制到Q。在其他任何时刻，因为总有一个阻塞的锁存器来阻断D到Q的通路，Q将保持原来的值不变。

总结就是一句话：

D触发器在时钟上升沿时将D值复制到Q，在其他时间D触发器保持原有的状态。

还有一个考点是晶体管数量的计算

构成一个与非门或者一个或非门需要用4个晶体管。

一个非门需要用2个晶体管。

一个与门可以由一个与非门和一个非门组成，所以它将用6个晶体管。

一个SR锁存器需要用2个或非门或8个晶体管。

一个D锁存器需要用一个SR锁存器、2个与门和一个非门或22个晶体管。

一个D触发器需要用两个D锁存器和一个非门或46个晶体管。

这个图形肯定可以区分出区别

寄存器

一个N位的寄存器由共享同一时钟的一排N个触发器组成，所以寄存器的所有位同时被更新。寄存器是组成时序电路的关键结构。

带使能端的触发器

当EN=1时，带使能端的触发器和普通的D触发器一样。当EN=0时，带使能端的触发器忽略时钟，保持原来的状态不变。当我们希望在某些时间（而不是在每一个时钟沿时）载入一个新值到触发器中时，带使能端的触发器非常有用。

带复位功能的触发器

带复位功能的触发器增加了一个输入RESET。当RESET=0时，带复位功能的触发器和普通的D触发器一样。当RESET=1时，带复位功能的触发器忽略D并且将输出Q复位为0。

触发器可能是异步复位或者同步复位；
同步复位功能的触发器仅仅在时钟上升沿时进行复位；
异步复位的触发器只要Reset=1就可以对它进行复位操作，而与时钟无关。

晶体管级的锁存器和触发器的设计

一个简洁的D锁存器可以用一个传输门构成，如图3-12a所示。当CLK=1和CLK=0时，传输门是开放的，于是D传输到Q，D锁存器是透明的。当CLK=0和CLK=1时，传输门是关闭的，于是D和Q之间隔离，D锁存器是阻塞的。

缺点：

输出节点浮空

没有缓冲

重点：

触发器和锁存器比较。

这个需要熟悉锁存器和触发器

输出Q上有一个小的延迟。

同步逻辑设计

非稳态电路。

同步时序电路

同步时序电路的组成规则告诉我们，如果一个电路是同步时序电路，它必须由相互连接的电路元件构成，且需要满足以下条件：

每一个电路元件要么是寄存器要么是组合电路；
至少有一个电路元件是寄存器；
所有寄存器接收同一个时钟信号；
每一个环路至少包含一个寄存器。

非同步时序电路称为异步（asynchronous）电路。

单个触发器是一个最简单的同步时序电路。

题目：

图3-21a的电路是组合逻辑电路，不是时序逻辑电路，因为它没有一个寄存器。

图3-21b的电路是一个不带反馈回路的简单时序电路。

图3-21c的电路既不是组合电路也不是时序电路，因为它有一个锁存器，这个锁存器既不是寄存器也不是组合逻辑电路。

图3-21d和图3-21e的电路是同步时序逻辑电路；它们是有限状态机的两种形式

图3-21f的电路既不是组合电路也不是时序电路，因为它有一个从组合逻辑电路的输出端电路反馈到同一逻辑电路输入端的回路，但是在回路上没有寄存器。

图3-21g的电路是同步时序逻辑电路的流水线形式

图3-21h的电路严格地说不是一个同步时序电路，因为两个寄存器的时钟信号不同，它们有两个反相器的延迟。

有限状态机

M位输入、N位输出和k位状态

1个时钟信号和一个可选的复位信号

包含两个组合逻辑块：下一状态的逻辑（next state logic）和输出逻辑（output logic），以及一组用于存储状态的寄存器。

在每一个时钟沿，有限状态机进入下一状态。这个下一状态是根据当前的状态和输入值计算出来的。

分类：

在Moore型有限状态机中，输出仅仅取决于当前的状态。

在Mealy型有限状态机中，输出取决于当前的状态和输入值。

设计实例

分别在Academic大道和Bravado大道上安装了两个交通传感器TA和TB。传感器上输出1时，表示此大道上有学生出现；输出0时，表示大道上没有人。Ben又安装了两个交通灯LA和LB来控制交通。每一个灯接收数字信号输入，以确定显示绿色、黄色或红色。所以，有限状态机有TA和TB两个输入，LA和LB两个输出。十字路口的灯和传感器如图3-23所示。Ben采用了一个周期为5秒的时钟。在每一个时钟上升沿，灯将根据传感器改变。同时，Ben还设计了一个复位按键以便技术员在打开交通灯时将控制器设置为一个已知的起始状态。状态机的黑盒视图如图3-24所示。

第二步是画出状态转换图（state transition diagram）

当系统复位时，Academic大道上的灯是绿色，Bravado大道上的灯是红色。

每5秒，控制器检查交通模式并决定下一步该如何处理。此时，若在Academic大道有交通，灯就不再改变。当Academic大道上没有交通时，此大道上的灯变成黄色并保持5秒，然后再变成红色，同时Bravado大道上的灯变成绿色。同样，在Bravado大道上有交通的时候，此大道上的灯保持绿色，然后变成黄色，最后变成红色。

标有Reset的圆弧从外部进入S0状态，这说明不管当前是什么状态，系统复位时都应该进入的状态。

在S0状态，如果TA为真，系统将保持当前状态；如果TA为假，将转换成S1状态。如果状态只有一个离开它的圆弧，不管输入是什么，转换都会发生。例如，在S1状态，系统将总是转换到S2状态。

将状态转换图重写为状态转换表（state transition table），如表3-1所示。它说明了每一种状态和输入值所产生的下一个状态S。表中使用了无关项（X），这表示下一个状态并不依赖于特定的输入。同时，在表中忽略了复位。

状态转换图中使用了抽象的状态标记{S0，S1，S2，S3}和输出标记{红灯，黄灯，绿灯}。为建立一个真实的电路，状态和输出必须按照二进制编码。

用二进制编码更新状态转换表

最后，绘制了Moore型有限状态机的电路图。。

Dynamic Discipline动态约束

同步时序电路输入在孔径时间内必须稳定

并行

并行有两类： >Two types of parallelism: >Spatial parallelism空间并行 >duplicate hardware performs multiple tasks at once >提供多个相同的硬件，多个任务在同一时间一起处理 >Temporal parallelism时间并行 task is broken into multiple stages一个任务被分成多个阶段 >also called pipelining流水线 >for example, an assembly line类似于流水线

有一些专有名词 token 任务 Latency 延迟 Throughput 吞吐量并行可以增加吞吐量课本的饼干例子： Latency = 5 + 15 = 20 minutes = 1/3 hour Throughput = 1 tray/ 1/3 hour = 3 trays/hour 采用空间并行的话，延迟并没有改变，但是吞吐量上升了一倍： Latency = 5 + 15 = 20 minutes = 1/3 hour Throughput = 2 trays/ 1/3 hour = 6 trays/hour

采用时间并行的话： Latency = 5 + 15 = 20 minutes = 1/3 hour Throughput = 1 trays/ 1/4 hour = 4 trays/hour

如果同时使用空间并行与时间并行技术，吞吐量是8盘/小时

第四章.硬件描述语言

Introduction引言 Combinational Logic组合逻辑 Structural Modeling结构建模 Sequential Logic时序逻辑 More Combinational Logic 更多组合逻辑 Finite State Machines有限状态机 Parameterized Modules参数化模块 Testbenches测试程序

行为模型和结构模型

一个是描述一个模块做什么

另一种是应用层次化方法描述一个模块怎么用更简单的部件构造

模块是模块化的一个好应用。

采取SystemVerilog，以模块名，输入列表和输出列表开始。

assign语句描述自组合逻辑

logic信号是布尔变量，有浮点值和未定义的值。

语言的目的是逻辑模拟和综合。（大写是敏感的，数字不能作为开头的，空白是可以忽略的，注释的实现，单行可以用横线，多行和C++一致）

模拟阶段，在模块上加入输入，并检查输出已验证模块的操作是否正确。在综合阶段，将模块的文字描述转换成逻辑门。

三态缓冲器

          moduletristate(input [3:0] a,

               input   en,

           output [3:0] y);

                 assign y = en ? a: 4'bz;

endmodule

a[3:0]就是一个代表四位的宗信啊是小端,为[N-1,0]

缩位运算符

条件赋值，可以用来实现复用器

内部变量：就是中间变量很好理解，

条件赋值运算符：和C++的？:一样属于三元运算符

优先级别：

可以加上括号

数字：

可以用用各种进制，下划线会被忽略，可以增加可读性。

形式是N`Bvalue,N是位数，B是说明基数的字母，value是数字。

9`h25表示是9位16进制数字，用16进制表示

b是二进制，o是八进制，d是十进制，h是十六进制，默认是10

Z和X

描述赋空值，适合三态缓冲器，如果一条总线被两个使能端的三态缓冲器同时驱动位0或1，x表示无效，如果所有三态缓冲器都是OFF，用Z表示浮空

真值表表示不确定

位混合

延迟

延迟模拟中有用，综合则基本没用

锁存器

module latch(input  logic       clk, 
             input  logic [3:0] d, 
             output logic [3:0] q);

  always_latch
    if (clk) q <= d;

endmodule

结构建模

行为是通过建立输入输出之间关系

结构则是描述怎么用更加简单的模块组成

2：1多路选择器的结构建模

访问总线的一部分

寄存器

module flop(input  logic       clk, 
            input  logic [3:0] d, 
            output logic [3:0] q);

  always @(posedge clk)
    q <= d;                // pronounced “q gets d”

endmodule

always语句会让信号保持他们的旧值直到一个敏感信号列表中的事件发合适呢个，此时会引起他们的值改变。

举有合适敏感信号列表的代码，可以用于描述用记忆功能的时序电路。

如clk，可以让q在下一个clk上升来临之前保持旧值。

上述采取<=是非阻塞式赋值，他的语句执行时同时执行的，是不会有先后顺序的。

带复位功能的寄存器

不同就在上面了，同步只会有一个。

module flopr(input  logic       clk,
             input  logic       reset, 
             input  logic [3:0] d, 
             output logic [3:0] q);
 
  // synchronous reset
  always @(posedge clk)
    if (reset) q <= 4'b0;
    else       q <= d;

endmodule

带使能端的寄存器

特点是使能有效时候才响应始终，

如果reset和en都是false的话就是会保持旧值

多寄存器

同步器就是在Clk的上升沿，d被赋值到N1，同时n1被复制到q

锁存器

当是high时候，D锁存器是透明，数据会从输入流向输出，在low时候是堵塞的，保持原有的状态。

case语句

使用case语句描述七段数码显示译码器，针对16种不同输入产生7位输出的只读存储器

译码器

module sevenseg(input  logic [3:0] data, 
                output logic [6:0] segments);
  always_comb
    case (data)
      //                     abc_defg     
      0: segments =       7'b111_1110;
      1: segments =       7'b011_0000;
      2: segments =       7'b110_1101;
      3: segments =       7'b111_1001;
      4: segments =       7'b011_0011;
      5: segments =       7'b101_1011;
      6: segments =       7'b101_1111;
      7: segments =       7'b111_0000;
      8: segments =       7'b111_1111;
      9: segments =       7'b111_0011;
      default: segments = 7'b000_0000; // required
    endcase
endmodule

module priority_casez(input  logic [3:0] a, 
                      output logic [3:0] y);
  always_comb
    casez(a)
      4'b1???: y = 4'b1000;  // ? = don’t care
      4'b01??: y = 4'b0100;
      4'b001?: y = 4'b0010;
      4'b0001: y = 4'b0001;
      default: y = 4'b0000;
   endcase
endmodule

if语句

在这种描述性语言中,if语句必须出现在always语句中

带有无关项的真值表

阻塞式和非阻塞式赋值

时序逻辑采用阻塞就出现错误了。

时序就必须使用非阻塞式赋值。

有限状态机

模式识别器与当前状态和输入都有关

模式识别器的mealy型的有限状态机

有限状态机主要有三部分代码需要进行编写：下一状态逻辑状态寄存器输出逻辑

module divideby3FSM (input  logic clk, 
                     input  logic reset, 
                     output logic q);
   typedef enum logic [1:0] {S0, S1, S2} statetype;
   statetype [1:0] state, nextstate;  
 
   // state register
   always_ff @ (posedge clk, posedge reset)
      if (reset) state <= S0;
      else       state <= nextstate;

   // next state logic
   always_comb
      case (state)
         S0:      nextstate = S1;
         S1:      nextstate = S2;
         S2:      nextstate = S0;
         default: nextstate = S0;
      endcase

   // output logic
   assign q = (state == S0);
endmodule

测试程序

用于测试其他待测试模块的硬件描述语言模块，包含了向待测试模块提供输入的语句，测试是否产生了理想的正确输出，输入和期待的输出模式称为测试向量。

能够自测试的测试程序

也是测试的一部分。

带测试向量的测试程序，从测试文件中中读取测试向量，

虽然时钟信号和复位信号在组合逻辑测试之中不是必须的，但也是包含在其中的。

example.tv是包含了二进制格式输入和期待输出的文本文件。

代码：

在时钟上升时候向待测试设备提供新输入，在始终下降时候检查输出，测试程序在发生错误时候会报告错误。模拟结束时候，打印使用的测试向量总数和检查到的错误数字。

常见数字模块

Introduction引言 Arithmetic Circuits算术电路 Number Systems数制系统 Sequential Building Blocks 时序电路模块 Memory Arrays存储器阵列 Logic Arrays逻辑阵列

一位全加器

三种进位传播加法器 ### Ripple-carry (slow) > 太慢了：$t_{ripple}$ = $Nt_{FA}$

Carry-lookahead (fast) 先行进位加法器

由输入的A，B算出每一位的G，P 计算k位块的G和P (由各位的G，P算出每一位的GN:0，PN:0 ) 由每一位的GN：0，PN：0与Cin算出每一位的Cout，S。其中第1，3步显然是可以并行处理的，计算的主要复杂度集中在了第2步。 For N-bit CLA with k-bit blocks:一个分解成k位块的N位加法器延迟为 tCLA = tpg + tpg_block + (N/k – 1)tAND_OR + ktFA

tpg : delay to generate all Pi, Gi 为单独一个生成产生信号P和传播G的门电路（一个单独的AND或者OR门电路） tpg_block : delay to generate all Pi:j, Gi:j 为在k位块中生成产生信号Pi:j和输出信号Gi:j的延迟 tAND_OR : delay from Cin to Cout of final AND/OR gate in k-bit CLA block 为在k位CLA块中Cin从AND/OR逻辑到Cout的延迟

当N > 16时，先行进位加法器一般总会比行波进位加法器块很多

Prefix (faster) 前缀加法器

要求掌握前两种

减法器：减法非常简单：改变减数的符号，然后做加法。改变二进制补码的符号就是翻转所有的位，然后加一 ### Shifters移位器

Logical shifter: 逻辑移位器 Ex: 11001 >> 2 = 00110 Ex: 11001 << 2 = 00100 Arithmetic shifter: 算术移位器 Ex: 11001 >>> 2 = 11110 Ex: 11001 <<< 2 = 00100 Rotator: 循环移位器 Ex: 11001 ROR 2 = 01110 Ex: 11001 ROL 2 = 00111 4位移位器：左移