数据结构之图的应用大题

01. 下面是一种称为“破圈法”的求解最小生成树的方法：所谓“破圈法”，是指“任取一圈，去掉圈上权最大的边”，反复执行这一步骤，直到没有圈为止。

问题：试判断这种方法是否正确。若正确，说明理由；若不正确，举出反例（注：圈就是回路）。

答案：该方法是正确的。

解释：

  1. 生成树的定义：
    • 生成树是图中能够连接所有顶点的无环连通子图。
    • 最小生成树（MST）是所有生成树中权值和最小的那一棵。
  2. 破圈法的思路：
    • 破圈法的核心是：每次在圈（回路）中删除权值最大的边。删除这条边后，回路被打破，保证了图中无环，且仍保持连通。
  3. 为什么最终生成的是一棵生成树：
    • 经过破圈法的不断删除，最终所有回路都会被去掉，剩下的结构就是一个无环连通图，也就是生成树。
  4. 证明生成的树是最小生成树：
    • 假设通过破圈法生成的树为 $ T $，但假设 $ T $ 不是最小生成树。
    • 设 $ T^* $ 是最小生成树，并且 $ T^* $ 和 $ T $ 的公共边尽可能多。
    • 如果 $ T^* $ 和 $ T $ 不同，必然存在一个回路，因为 $ T $ 是通过破圈法构造的，且破圈法会在回路中删除权值最大的边，而这条边在最小生成树中不会出现。
    • 根据破圈法定义，每次删除的都是权值最大的边，这保证了最终构造的树的权值不会比最小生成树的权值大。因此，生成的 $ T $ 也是最小生成树。
  5. 反证法：
    • 假设 $ T $ 不是最小生成树，则必然存在一条边的权值比破圈法删除的边小，这与破圈法删除最大权值边的定义矛盾，因此假设不成立， $ T $ 是最小生成树。

因此，破圈法正确地构造出的是最小生成树。

image-20241009101219705
image-20241009101229009

02. 已知有向图如下图所示。

问题：

  1. 写出该图的邻接矩阵表示并据此给出从顶点 1 出发的深度优先遍历序列。
  2. 求该有向图的强连通分量的数目。
  3. 给出该图的任意两个拓扑序列。
  4. 若将该图视为无向图，分别用 Prim 算法和 Kruskal 算法求最小生成树。
image-20241009101454832

答案：

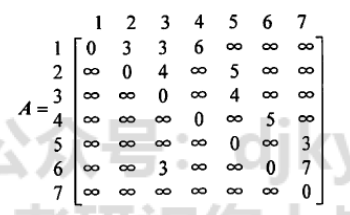
  1. 邻接矩阵表示：

    • 假设图中有 7 个顶点 $ V_1, V_2, V_3, V_4, V_5, V_6, V_7 $，并给出它们之间的有向边。
    • 邻接矩阵 $ A $ 为： image-20241009101535203
    • 深度优先遍历序列：
      • 深度优先遍历（DFS）序列：1,2,3,5,7,4,6。

  2. 强连通分量的数目：

    • 强连通分量指的是一个有向图中，顶点之间互相可达的最大子图。
    • 从图的结构可以看出，没有任何顶点可以互相到达，因此每个顶点本身就是一个强连通分量。
    • 强连通分量数目为 7，说明图中的每个顶点都是独立的强连通分量。

  3. 两个拓扑序列：

    • 拓扑排序是对有向无环图（DAG）的顶点进行排序，使得对每条有向边 $ (u, v) $，顶点 $ u $ 在 $ v $ 之前出现。
    • 对于这个图，可能的拓扑序列有很多。
    • 任意两个拓扑序列为：
      1. 1, 2, 4, 6, 3, 5, 7
      2. 1, 4, 2, 6, 3, 5, 7

  4. 最小生成树（视为无向图）：

    • 若将该图视为无向图，可以用 Prim 和 Kruskal 算法来求最小生成树。

    Prim 算法：

    • 从顶点 1 开始，逐步扩展到其他顶点，选择当前连接权值最小的边。
    • 过程：1-2, 1-3, 3-6, 3-5, 5-7, 6-4。
    • 最小生成树的边为：1-2, 1-3, 3-6, 3-5, 5-7, 6-4。

    Kruskal 算法：

    image-20241009101737090
    image-20241009101755315

问题03：

根据下图所示的无向图，使用 Dijkstra 算法，写出从 顶点1 到其他各个顶点的最短路径和最短路径长度。请确保路径顺序不能颠倒。

解答：

1) Dijkstra 算法简介：

Dijkstra 算法用于求解从源点（起始顶点）到所有其他顶点的最短路径。它的基本思想是从源点开始，逐步构建一个最短路径的集合。在每一步中，找到到当前集合中未访问顶点的最短路径并更新其路径值，直到所有顶点都访问完毕。

算法的步骤：

  1. 将所有顶点的初始距离设置为 ∞（无穷大），源点的距离为 0。
  2. 在每次迭代中，选择距离源点最近且未访问过的顶点作为当前顶点。
  3. 更新与当前顶点直接相邻的顶点的距离，如果找到更短的路径则更新。
  4. 重复步骤 2 和 3，直到所有顶点都访问过。
image-20241009140400328

如图所示：

image-20241009140758472

问题04：

下图所示为一个用 AOE 网（Activity On Edge network）表示的工程。要求完成以下任务：

  1. 画出此图的邻接表表示。
image-20241009140221125

该图的邻接表表示如下图所示。

image-20241009140922613

问题06：

如何利用深度优先搜索 (DFS) 实现有向无环图 (DAG) 的拓扑排序？请说明具体步骤并提供解释。

解答：

在有向无环图 (DAG) 中，拓扑排序是一种线性排序，使得对于每一条有向边 $ u v $，节点 $ u $ 在排序中排在节点 $ v $ 之前。使用深度优先搜索 (DFS) 来实现拓扑排序的基本思想是基于节点的结束时间。

实现步骤：

  1. 初始化：
    • 创建一个访问标记数组 visited，用于标记每个节点是否已被访问。
    • 创建一个数组 finishTime，用于存储每个节点的结束时间。
    • 初始化一个全局时间变量 time，用于记录访问的时间。
  2. 深度优先搜索 (DFS)：
    • 对于每个未被访问的节点 $ v $，调用 DFS 函数。
    • 在 DFS 函数中，标记当前节点 $ v $ 为已访问，并对其进行处理（如打印或记录）。
    • 递归访问所有未被访问的邻接节点 $ w $。
    • 在递归返回时，增加 time，并将当前节点 $ v $ 的结束时间记录在 finishTime 中。
  3. 记录结束时间：
    • 每当一个节点的 DFS 调用完成（即所有邻接节点都已被访问），就记录其结束时间。这一过程确保了祖先节点的结束时间在子孙节点结束时间之前。
  4. 构建拓扑排序：
    • 一旦所有节点的 DFS 调用完成，将节点按结束时间的逆序排列，即从大到小排序。这就是所需的拓扑排序。

代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <iostream>
#include <vector>
#include <algorithm>

#define MAX_VERTEX_NUM 100

using namespace std;

bool visited[MAX_VERTEX_NUM];
int finishTime[MAX_VERTEX_NUM];
int time = 0;

struct Graph {
    int vexnum; // 节点数
    vector<int> adj[MAX_VERTEX_NUM]; // 邻接表表示图
};

void DFS(Graph &G, int v) {
    visited[v] = true; // 标记当前节点为已访问
    for (int w : G.adj[v]) { // 遍历所有邻接节点
        if (!visited[w]) {
            DFS(G, w); // 递归访问
        }
    }
    finishTime[v] = ++time; // 记录结束时间
}

void DFSTraverse(Graph &G) {
    for (int v = 0; v < G.vexnum; ++v) {
        visited[v] = false; // 初始化访问标记
    }
    time = 0; // 重置时间
    for (int v = 0; v < G.vexnum; ++v) {
        if (!visited[v]) {
            DFS(G, v); // 从未访问的节点开始 DFS
        }
    }
}

void TopologicalSort(Graph &G) {
    DFSTraverse(G); // 进行深度优先遍历

    // 按结束时间从大到小排序
    vector<pair<int, int>> finishPairs; // 存储节点及其结束时间
    for (int v = 0; v < G.vexnum; ++v) {
        finishPairs.push_back(make_pair(finishTime[v], v));
    }
    sort(finishPairs.rbegin(), finishPairs.rend()); // 从大到小排序

    // 输出拓扑排序结果
    cout << "Topological Order: ";
    for (auto &p : finishPairs) {
        cout << p.second << " "; // 输出节点
    }
    cout << endl;
}

int main() {
    Graph G;
    G.vexnum = 6; // 假设图有6个节点
    G.adj[0] = {1, 2};
    G.adj[1] = {3};
    G.adj[2] = {3, 4};
    G.adj[3] = {5};
    G.adj[4] = {5};
    G.adj[5] = {};

    TopologicalSort(G); // 执行拓扑排序
    return 0;
}

解释：

  • 访问标记：用来避免重复访问同一节点，确保 DFS 的正确性。
  • 结束时间：通过结束时间的逆序来获得拓扑排序，因为在 DAG 中，任何一个节点的结束时间都会大于其所有子孙节点的结束时间。
  • 排序：使用 STL 的排序功能，根据结束时间的大小来排列节点，从而形成拓扑序列。

这种方法的时间复杂度为 $ O(V + E) $，其中 $ V $ 是节点数，$ E $ 是边数，适用于高效地处理大型图的拓扑排序。

问题07：

给定一个连通无向图，边的权值为非负数，使用 Dijkstra 最短路径算法能否得到一棵生成树？该生成树是否一定是最小生成树？请说明理由。

解答：

结论：

  1. Dijkstra 算法可以得到一棵生成树：Dijkstra 最短路径算法从一个起始顶点开始，逐步找到从起始顶点到其他所有顶点的最短路径，在此过程中构造出了一棵以起始顶点为根的生成树。

  2. Dijkstra 算法生成的树不一定是最小生成树：Dijkstra 算法的目标是找到从起始顶点到其他顶点的最短路径，而最小生成树 (MST) 的目标是找到一个包含所有顶点且权重和最小的无环子图。这两个问题的目标不同，虽然 Dijkstra 算法可以产生一棵生成树，但它不保证是所有边权和最小的树，因此不能保证它一定是最小生成树。

详细解释：

1. Dijkstra 算法生成的树：

  • Dijkstra 是一种 贪心算法，通过优先选择具有最短路径的顶点来逐步扩展结果。算法从起始顶点出发，逐个选择距离起始点最短的未访问顶点，将其加入已访问的集合，直到所有顶点都被访问完毕。
  • 在每一步中，Dijkstra 会选择从当前顶点集合出发到未访问顶点中距离最短的一条边，并将对应的顶点添加到树中。因此，最终会构造出一棵生成树，其中每个顶点与它的前驱顶点通过最短路径连接。

2. 为什么 Dijkstra 生成的树不一定是最小生成树？

  • Dijkstra 的目标是最短路径：Dijkstra 算法的目的是找到从 单一源点 到其他所有顶点的最短路径，因此在每一步选择的边是为了最短路径服务。
  • 最小生成树的目标是最小权重和：最小生成树算法（如 Prim 或 Kruskal）是为了找到一棵连接所有顶点的无环树，使得树中所有边的权重和最小。
  • 区别在于目标不同：Dijkstra 关注的是 单源最短路径，而最小生成树关注的是 所有边权和最小。因此，Dijkstra 生成的路径可能并不满足最小生成树的条件，即使边的权重是非负的。
image-20241009141628904

Dijkstra 算法得到的路径集合为\({(a,b),(a,c),(a,d)}\)，该生成树的总权值为\(5+5+5=15\)。

Prim 算法得到的边集合为\({(a,d),(b,d),(c,d)}\)，该最小生成树的总权值为\(5+1+1=7\). 显然，Diikstra 算法得到的生成树不一定是最小生成树。

问题08：

给定一个带权图（边权值为非负，表示连接两顶点之间的距离），是否可以用以下方法求解从初始顶点到目标顶点之间的一条最短路径？

  1. 设最短路径初始时仅包含初始顶点，令当前顶点 u 为初始顶点。
  2. 选择离 u最近且尚未在最短路径中的一个顶点 v，加入最短路径，修改当前顶点 u 为 v。
  3. 重复步骤 2，直到 u 是目标顶点时为止。

该方法可否求得最短路径？若可行，请证明；若不可行，请举例说明。

解答：

结论： 上述方法 不一定能求得最短路径。

理由： 这种方法的选择过程与 Dijkstra 算法相似，但有一个关键问题在于它只考虑了当前最邻近的顶点 v，而没有考虑到可能通过其他顶点 u 到达目标顶点的更短路径。因此，算法在每一步中做出的局部最优选择可能会导致全局最优解的失败。

若按照题中的原则，从A到C的最短路径是A→B→C，事实上其最短路径是 A→D→C。

image-20241009141754626

问题10：

已知有6个顶点（顶点编号为0~5）的有向带权图 $ G $，其邻接矩阵 $ A $ 为上三角矩阵，按行为主序（行优先）保存在如下的一维数组中：

要求：

  1. 写出图 $ G $ 的邻接矩阵。
  2. 画出有向带权图 $ G $。
  3. 求图 $ G $ 的关键路径，并计算该关键路径的长度。
image-20241009141214077

图G的邻接矩阵A为:

image-20241009141833301

有向带权图 G如下图所示:

image-20241009141843358

关键路径为0-1→2-3-5(如下图中的粗线表示)，长度为4+5+4+3=16。

image-20241009141902428

问题11：

使用 Prim 算法求带权连通图的最小生成树（MST）。请回答下列问题：

  1. 对下列图 G，从顶点 A 开始求 G 的 MST，依次给出按算法选出的边。
  2. 图 G 的 MST 是唯一的吗？
  3. 对任意的带权连通图，满足什么条件时，其 MST 是唯一的？

解答：

  1. 使用 Prim 算法求最小生成树（MST）：

    Prim 算法是一种贪心算法，它从一个任意的顶点开始，逐步扩展最小生成树。算法的步骤如下：

    • 初始化：从顶点 A 开始，创建一个集合 S 来存储已加入的顶点。初始时，S 只包含顶点 A。
    • 选择边：在连接集合 S 中的顶点与其他顶点的边中，选择权重最小的边，将其对应的顶点加入集合 S。

    具体步骤如下：

    1. 初始状态：S = {A}
      • 候选边：$ (A, B), (A, D), (A, E) $
      • 选择边：$ (A, D) $（假设权重最小）
    2. 状态更新：S = {A, D}
      • 候选边：$ (A, B), (D, C), (D, E) $
      • 选择边：$ (D, E) $
    3. 状态更新：S = {A, D, E}
      • 候选边：$ (A, B), (E, C) $
      • 选择边：$ (E, C) $
    4. 状态更新：S = {A, D, E, C}
      • 候选边：$ (A, B), (C, B) $
      • 选择边：$ (C, B) $
    5. 完成：S = {A, D, E, C, B}

    选出的边依次为：

    • $ (A, D) $
    • $ (D, E) $
    • $ (E, C) $
    • $ (C, B) $

  2. 图 G 的 MST 是唯一的吗？

    是的，图 G 的最小生成树（MST）是唯一的。对于本题中的最小生成树，所选择的边都具有唯一的最小权重，因此没有其他组合能够替代这些边而不形成回路。

  3. 对任意的带权连通图，满足什么条件时，其 MST 是唯一的？

    当带权连通图的任意环中所包含的边的权值均不相同时，其最小生成树（MST）是唯一的。具体来说，若图中没有两条边的权重相同，则最小生成树是唯一的，因为任何权值相同的边都可能导致不同的 MST。

image-20241009141334330