数据结构之查找树选择题

单项选择题

01 对于二叉排序树，下面的说法中，( )是正确的。

A. 二叉排序树是动态树表，查找失败时插入新节点，会引起树的重新分裂和组合
B. 对二叉排序树进行层序遍历可得到有序序列
C. 用逐点插入法构造二叉排序树，若先后插入的关键字有序，二叉排序树的深度最大
D. 在二叉排序树中进行查找，关键字的比较次数不超过节点数的 $ $

答案：C
解释：

A选项错误，二叉排序树插入新节点时不会引起树的分裂和组合。
B选项错误，层序遍历并不能保证得到有序序列，只有中序遍历才可以。
C选项正确，逐点插入法构造的二叉排序树，如果先后插入的关键字有序，则树会形成一条长链，此时深度最大。
D选项错误，查找时关键字的比较次数可能超过节点数的一半。

02 按()遍历二叉排序树得到的序列是一个有序序列。

A. 先序
B. 中序
C. 后序
D. 层次

答案：B
解释：
中序遍历二叉排序树的特性决定了在遍历过程中，左子树的节点总是先于根节点，而根节点总是先于右子树的节点，因此得到的序列是有序的。

03 在二叉排序树中进行查找的效率与()有关。

A. 二叉排序树的深度
B. 二叉排序树的节点的个数
C. 被查找节点的度
D. 二叉排序树的存储结构

答案：A
解释：
查找效率主要取决于二叉排序树的高度，树的高度越小，查找效率越高。虽然节点的个数和存储结构也会影响查找效率，但关键因素还是树的深度。

04 在常用的描述二叉排序树的存储结构中，关键字值最大的节点()。

A. 左指针一定为空
B. 右指针一定为空
C. 左右指针均为空
D. 左右指针均不为空

答案：B
解释：
在二叉排序树中，关键字值最大的节点位于最右侧，其右指针一定为空。因为如果右指针不为空，则右指针指向的节点的值一定大于当前节点的值，导致当前节点不再是最大的关键字。

05 设二叉排序树中关键字由1到1000的整数构成，现要查找关键字为363的节点，下述关键字序列中，不可能是在二叉排序树上查找的序列是()。

A. 2, 252, 401, 398, 330, 344, 397, 363
B. 924, 220, 911, 244, 898, 258, 362, 363
C. 925, 202, 911, 240, 912, 245, 363
D. 2, 399, 387, 219, 266, 382, 381, 278, 363

答案：C
解释：
在二叉排序树中查找时，首先与根节点值进行比较，若相同则查找结束，若不同则根据比较结果继续向左或向右子树查找。根据二叉排序树的定义，左子树节点的值 ≤ 根节点值 ≤ 右子树节点的值。

在C序列中，首先比较911（大于363），所以应转向911的左子树继续查找。此时，240的右子节点是912（大于911），这与二叉排序树的性质矛盾，因为911的左子树中不应该有大于911的节点。因此，C序列不可能是在二叉排序树上查找的序列。

06分别以下列序列构造二叉排序树，与用其他3个序列所构造的结果不同的是()。

A. (100, 80, 90, 60, 120, 110, 130)
B. (100, 120, 110, 130, 80, 60, 90)
C. (100, 60, 80, 90, 120, 110, 130)
D. (100, 80, 60, 90, 120, 130, 110)

答案：C
解释：
在构造二叉排序树时，节点的插入顺序决定了树的结构。通过分析各个选项的插入顺序，我们可以发现：

A、B和D的插入顺序会导致相似的结构，因为这些序列会按照相同的逻辑插入节点。
但在C序列中，首先插入的60会作为100的左子树，而后面的80和90都将在60的右边，这会导致树的结构不同于其他选项。因此，C序列构造的结果与其他三个选项不同。

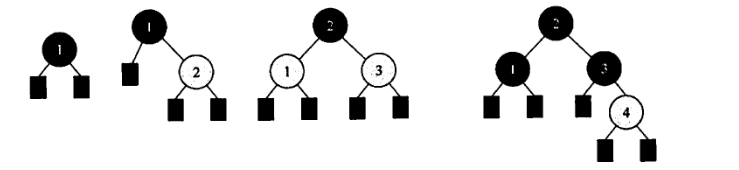
07 从空树开始，依次插入元素 52, 26, 14, 32, 71, 60, 93, 58, 24 和 41 后构成了一棵二叉排序树。在该树查找60要进行比较的次数为()。

A. 3
B. 4
C. 5
D. 6

答案：A

以第一个元素为根结点，依次将元素插入树，生成的二叉排序树如右图所示。进行查找时，先与根结点比较，然后根据比较结果，继续在左子树或右子树上进行查找。比较的结点依次为52,71,60。

08 在含有n个结点的二叉排序树中查找某个关键字的结点时，最多进行()次比较。

A. n/2
B. 10g(n)
C. log2(n) + 1
D. n

答案：D
解释：
在最坏的情况下，二叉排序树可能会退化为一条链表（例如，当插入的元素是有序的）。此时，在查找一个关键字时，可能需要比较所有的n个节点，因此最多需要进行n次比较。

9 构造一棵具有 $ n $ 个结点的二叉排序树时，最理想情况下的深度为()。

A. $ n/2 $
B. $ n $
C. $ _2(n + 1) $
D. $ _2(n + 1) $

答案：D
解释：
在最理想的情况下，二叉排序树是完全平衡的，即每一层都尽可能地被填满。此时，树的深度（或高度）是 $\lceil \log_2(n + 1) \rceil$。这个表达式表示了树的最小深度，确保在包含 $ n $ 个结点的情况下能够容纳这些结点。因此，正确答案是 D。

10 不可能生成如下图所示的二叉排序树的关键字序列是()。

A. $4, 2, 1, 3, 5$
B. $4, 2, 5, 3, 1$
C. $4, 5, 2, 1, 3$
D. $4, 5, 1, 2, 3$

答案：D
解释：
选项D中，插入1后，再插入2，2应作为1的右孩子结点，再插入3，3 应作为2的右孩子结点。故选D。选项D对应的二叉排序树如右图所示。

11 含有 20 个结点的平衡二叉树的最大深度为()。

A. 4
B. 5
C. 6
D. 7

答案：B
解释： 对于 AVL 树，最小的结点数与层数的关系可由以下递归关系给出：

$ N(h) = N(h-1) + N(h-2) + 1 $

由递推公式可以得到构造20个结点至少需要6层。

12 具有 5 层结点的 AVL 至少有( )个结点。

A. 10
B. 12
C. 15
D. 17

答案：C
解释：
对于 AVL 树，最小的结点数与层数的关系可由以下递归关系给出：

$ N(h) = N(h-1) + N(h-2) + 1 $

其中，$ N(h) $ 为高度为 $ h $ 的 AVL 树中至少有多少个结点。计算可以得到：

$ N(1) = 1 $
$ N(2) = 2 $
$ N(3) = 4 $
$ N(4) = 7 $
$ N(5) = 12 $

所以，具有 5 层结点的 AVL 树至少有 12 个结点，因此答案为 B。

13 下列关于红黑树的说法中，不正确的是()。

A. 一棵含有 $ n $ 个结点的红黑树的高度至多为 $ 2 _2(n + 1) $
B. 如果一个结点是红色的，则它的父结点和孩子结点都是黑色的
C. 从一个结点到其子孙结点的所有路径上包含相同数量的黑结点
D. 红黑树的查询效率一般要优于含有相同结点数的 AVL 树

答案：D
解释：
红黑树和 AVL 树都是自平衡的二叉搜索树，但 AVL 树是高度平衡的，其在插入和删除时的旋转次数较多。因此，AVL 树在查询操作上的效率一般优于红黑树。选项 A、B 和 C 都是红黑树的正确特性。

14 下列关于红黑树和 AVL 树的描述中，不正确的是()。

A. 两者都属于自平衡的二叉树
B. 两者查找、插入、删除的时间复杂度都相同
C. 红黑树插入和删除过程至多有 2 次旋转操作
D. 红黑树的任一结点的左右子树高度之差不超过 2 倍

答案：C
解释：
红黑树的插入和删除过程可能需要多次旋转（通常在 2 次以上），特别是在某些情况下（如插入和删除后需要调整树的性质时）。因此，C 选项是不正确的。选项 A 和 B 是正确的，红黑树和 AVL 树都是自平衡的树，且在理论上它们的查找、插入和删除的时间复杂度都是 $ O(n) $，但 AVL 树在这些操作上的常数因子更小。D 选项描述的是红黑树的性质，也正确。

15 下列关于红黑树的说法中，正确的是()。

A. 红黑树是一种特殊的平衡二叉树
B. 如果红黑树的所有结点都是黑色的，那么它一定是一棵满二叉树
C. 红黑树的任何一个分支结点都有两个非空孩子结点
D. 红黑树的子树也一定是红黑树

答案：B
解释： 选项 B 是正确的，因为如果红黑树的所有节点都是黑色的，那么它实际上会是一个满二叉树。满二叉树的每一层都被填满，红黑树的性质确保了这样的结构。

选项 A 是错误的，红黑树是一种自平衡的二叉搜索树，但不严格符合所有平衡二叉树的定义。
选项 C 是错误的，因为红黑树的分支节点不一定都有两个非空孩子结点，叶子结点（没有孩子的结点）在红黑树中是允许的。
选项 D 也是错误的，因为虽然红黑树的子树可以遵循红黑树的特性，但并不是每个子树都能保持所有红黑树的性质，特别是关于高度和黑色节点数量的限制。

16 将关键字 1, 2, 3, 4, 5, 6, 7 依次插入初始为空的红黑树 T，则 T 中红结点的个数是()。

A. 1
B. 2
C. 3
D. 4

答案：B
解释：
因此答案为 B。

17 将关键字 5, 4, 3, 2, 1 依次插入初始为空的红黑树 T，则 T 的最终形态是( )。

选项

18 下列二叉排序树中，满足平衡二叉树定义的是( )。

答案：B

根据平衡二叉树的定义有，任意结点的左、右子树高度差的绝对值不超过1。而其余3个答案均可以找到不满足条件的结点。

19 在下图所示的平衡二叉树中插入关键字 48 后，得到一棵新平衡二叉树，在新平衡二叉树中，关键字 37 所在结点的左、右子结点中保存的关键字分别是()。

A. 13, 48
B. 24, 48
C. 24, 53
D. 24, 90

答案： B

解释：
插入关键字 48 后，关键字 37 的右子结点将变为 48，因为 48 大于 37。根据平衡二叉树的性质，左子树中应保存小于 37 的关键字，而最接近 37 的关键字是 24。因此，关键字 37 的左、右子结点中保存的关键字分别是 24 和 48。

20 对下列关键字序列，不可能构成某二叉排序树中一条查找路径的是( )。

A. 95, 22, 91, 24, 94, 71
B. 92, 20, 91, 34, 88, 35
C. 21, 89, 77, 29, 36, 38
D. 12, 25, 71, 68, 33, 34

答案： A
解释：
在二叉排序树中，左子树结点值小于根结点，右子树结点值大于根结点。在选项A中，当查找到 91后再向 24查找，说明这一条路径(左子树)之后查找的数都要比91小，而后面却查找到了 94，因此错误，故选A。

21 若平衡二叉树的高度为 6，且所有非叶子结点的平衡因子均为 1，则该平衡二叉树的结点总数为()。

A. 12
B. 20
C. 32
D. 33

答案： B
解释：
平衡因子为 1 表示每个节点的左右子树高度差为 1。在这种情况下，构造的树将是最优的，即左子树的高度为 5，右子树的高度为 6。对于高度为 6 的树，其结点数计算公式为 $C(n) = C(n-1) + C(n-2) + 1$。经过计算可得，结点数为 20，因此答案为 B。