最短路

【模板】单源最短路径（标准版）

题目背景

2018 年 7 月 19 日，某位同学在 NOI Day 1 T1 归程 一题里非常熟练地使用了一个广为人知的算法求最短路。

然后呢？

\(100 \rightarrow 60\)；

\(\text{Ag} \rightarrow \text{Cu}\)；

最终，他因此没能与理想的大学达成契约。

小 F 衷心祝愿大家不再重蹈覆辙。

题目描述

给定一个 \(n\) 个点，\(m\) 条有向边的带非负权图，请你计算从 \(s\) 出发，到每个点的距离。

数据保证你能从 \(s\) 出发到任意点。

输入格式

第一行为三个正整数 \(n, m, s\)。 第二行起 \(m\) 行，每行三个非负整数 \(u_i, v_i, w_i\)，表示从 \(u_i\) 到 \(v_i\) 有一条权值为 \(w_i\) 的有向边。

输出格式

输出一行 \(n\) 个空格分隔的非负整数，表示 \(s\) 到每个点的距离。

样例 #1

样例输入 #1

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

样例输出 #1

0 2 4 3

提示

样例解释请参考 数据随机的模板题。

\(1 \leq n \leq 10^5\)；

\(1 \leq m \leq 2\times 10^5\)；

\(s = 1\)；

\(1 \leq u_i, v_i\leq n\)；

\(0 \leq w_i \leq 10 ^ 9\),

\(0 \leq \sum w_i \leq 10 ^ 9\)。

本题数据可能会持续更新，但不会重测，望周知。

2018.09.04 数据更新 from @zzq

#include<bits/stdc++.h>
using namespace std;
#define PII pair<int ,int>
const int INF=1e10;
const int N=1000010;
int n,m,s;
int dis[N];
int vis[N];
vector<PII>E[N];
void dj(int s)
{
	for(int i=1;i<=n;i++)
	{
		dis[i]=INF;
		vis[i]=0;
	}
    //初始化每个点都没有去过
	dis[s]=0;
    //距离为0
	priority_queue<PII,vector<PII>,greater<PII> >q;
	q.push({0,s});
    //放进去
	while(!q.empty())
{
int t=q.top().second;
	q.pop();
		if(vis[t])
        {
			continue;
		}
        //访问过就跳过
		vis[t]=1;	
        //不然标记为已经访问过哦
	for(int i=0,l=E[t].size();i<l;i++)
        //枚举他到的边
	{
		int v=E[t][i].first;
        //这是到哪个边
		int w=E[t][i].second;
        //权值
		if(dis[v]>dis[t]+w)
		{		
			dis[v]=dis[t]+w;
            //如果当前这个点离这个边的距离比我们到当前点的距离+权值还大
			q.push({dis[v],v});
            //更新并放入		
		}		
		}		
	}	
	}
int main()
{
	 ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>n>>m>>s;
int u,v,w;
for(int i=0;i<m;i++)
{
	cin>>u>>v>>w;
	E[u].push_back({v,w});
    //邻接表存储到哪个边和权值
	}	
	dj(s);
    //然后进入算法，直接从s开始
	for(int i=1;i<=n;i++)
	{
		cout<<dis[i]<<" ";
        //计算距离，单源
	}
	return 0;
}

[JLOI2011] 飞行路线

题目描述

Alice 和 Bob 现在要乘飞机旅行，他们选择了一家相对便宜的航空公司。该航空公司一共在 \(n\) 个城市设有业务，设这些城市分别标记为 \(0\) 到 \(n-1\)，一共有 \(m\) 种航线，每种航线连接两个城市，并且航线有一定的价格。

Alice 和 Bob 现在要从一个城市沿着航线到达另一个城市，途中可以进行转机。航空公司对他们这次旅行也推出优惠，他们可以免费在最多 \(k\) 种航线上搭乘飞机。那么 Alice 和 Bob 这次出行最少花费多少？

输入格式

第一行三个整数 \(n,m,k\)，分别表示城市数，航线数和免费乘坐次数。

接下来一行两个整数 \(s,t\)，分别表示他们出行的起点城市编号和终点城市编号。

接下来 \(m\) 行，每行三个整数 \(a,b,c\)，表示存在一种航线，能从城市 \(a\) 到达城市 \(b\)，或从城市 \(b\) 到达城市 \(a\)，价格为 \(c\)。

输出格式

输出一行一个整数，为最少花费。

样例 #1

样例输入 #1

5 6 1
0 4
0 1 5
1 2 5
2 3 5
3 4 5
2 3 3
0 2 100

样例输出 #1

8

提示

数据规模与约定

对于 \(30\%\) 的数据，\(2 \le n \le 50\)，\(1 \le m \le 300\)，\(k=0\)。

对于 \(50\%\) 的数据，\(2 \le n \le 600\)，\(1 \le m \le 6\times10^3\)，\(0 \le k \le 1\)。

对于 \(100\%\) 的数据，\(2 \le n \le 10^4\)，\(1 \le m \le 5\times 10^4\)，\(0 \le k \le 10\)，\(0\le s,t,a,b < n\)，\(a\ne b\)，\(0\le c\le 10^3\)。

另外存在一组 hack 数据。

本题是分层图裸题

分层图是指有很多个平行的图，各个平行的图之间有特殊的连接边。

本题就是各层之间建边时，建一条从上到下花费为0的边，代表免费乘坐一次。跑一遍从s到n*k+t的最短路即可。

#include <bits/stdc++.h>
using namespace std;
using ll=long long;
const int MAXN = 2e5, MAXM = 5e6;
int n, m, k, s, t, tot, ans = 0x7fffffff, head[MAXN + 5], dis[MAXN + 5];
bool vis[MAXN + 5];
struct Edge
{
	int next, to, dis;
} e[MAXM + 5];
struct Node
{
	int val, id;
friend bool operator<(Node x, Node y)
	{
		return x.val > y.val;
	}
};
 void addEdge(int u, int v, int w)
{
	e[++tot] = (Edge){head[u], v, w};
	head[u] = tot;
}
 void dijkstra(int s)
{ 
	memset(dis, 0x3f, sizeof(dis));
	priority_queue<Node> q;
	dis[s] = 0;
	q.push((Node){0, s});
	while(!q.empty())
	{
		int u = q.top().id;
		q.pop();
		if (vis[u])
			continue;
		vis[u] = 1;
		for (int v, w, i = head[u]; v = e[i].to, w = e[i].dis, i; i = e[i].next)
			if (dis[v] > dis[u] + w)
			{
				dis[v] = dis[u] + w;
				if (!vis[v])
					q.push((Node){dis[v], v});
			}
	}
}
int main()
{
	cin>>n>>m>>k>>s>>t;
	++s, ++t; 
	//节点编号改一下
	for (int u, v, w, i = 1; i <= m; ++i)
	{
		cin>>u>>v>>w;
		++u, ++v;
		addEdge(u, v, w), addEdge(v, u, w);
		for (int j = 1; j <= k; ++j)
		{ 
			// 一共 k 层
			addEdge(u + (j - 1) * n, v + j * n, 0), addEdge(v + (j - 1) * n, u + j * n, 0);
			// 这里连接的是层次与层次之间的关系
			addEdge(u + j * n, v + j * n, w), addEdge(v + j * n, u + j * n, w);
			//这里是每一层各个元素之间的关系
		}
	}
	dijkstra(s);
	for (int i = 0; i <= k; ++i)
		ans = min(ans, dis[t + i * n]);
	// 可能没有用完 k 次机会，所以要取到每一层终点最短路的最小值
	cout<<ans<<'\n';
	//输出答案
	return 0;
}

【模板】负环

题目描述

给定一个 \(n\) 个点的有向图，请求出图中是否存在从顶点 \(1\) 出发能到达的负环。

负环的定义是：一条边权之和为负数的回路。

输入格式

本题单测试点有多组测试数据。

输入的第一行是一个整数 \(T\)，表示测试数据的组数。对于每组数据的格式如下：

第一行有两个整数，分别表示图的点数 \(n\) 和接下来给出边信息的条数 \(m\)。

接下来 \(m\) 行，每行三个整数 \(u, v, w\)。

• 若 \(w \geq 0\)，则表示存在一条从 \(u\) 至 \(v\) 边权为 \(w\) 的边，还存在一条从 \(v\) 至 \(u\) 边权为 \(w\) 的边。
• 若 \(w < 0\)，则只表示存在一条从 \(u\) 至 \(v\) 边权为 \(w\) 的边。

输出格式

对于每组数据，输出一行一个字符串，若所求负环存在，则输出 YES，否则输出 NO。

样例 #1

样例输入 #1

2
3 4
1 2 2
1 3 4
2 3 1
3 1 -3
3 3
1 2 3
2 3 4
3 1 -8

样例输出 #1

NO
YES

提示

数据规模与约定

对于全部的测试点，保证：

• \(1 \leq n \leq 2 \times 10^3\)，\(1 \leq m \leq 3 \times 10^3\)。
• \(1 \leq u, v \leq n\)，\(-10^4 \leq w \leq 10^4\)。
• \(1 \leq T \leq 10\)。

提示

请注意，\(m\) 不是图的边数。

SPFA算法思路

我们用数组dis记录每个结点的最短路径估计值，用邻接表或邻接矩阵来存储图G。我们采取的方法是动态逼近法：设立一个先进先出的队列用来保存待优化的结点，优化时每次取出队首结点u，并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作，如果v点的最短路径估计值有所调整，且v点不在当前的队列中，就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作，直至队列空为止

#include <cstdio>
#include <iostream>
#include <queue>
#include <vector>
#include <cstring>
using namespace std;
vector <pair<int, int> > G[2001];
int T,n,m,u,v,w;
int dis[10000];
int cnt[10000];
bool in[10000];
void spfa()
{
	memset(dis, 0x3f3f, sizeof(dis));
	memset(in, 0, sizeof(in));
	memset(cnt, 0, sizeof(cnt));
	queue <int> q;
	q.push(1);
	dis[1]=0;
	in[1]=1;
	cnt[1]=1;
	while(!q.empty())
	{
		u=q.front();
		q.pop();
		in[u]=0;
		for(int i=0;i<G[u].size();i++)
		{
			v=G[u][i].first;
			w=G[u][i].second;
			if(dis[v]>dis[u]+w)
			{
				dis[v]=dis[u]+w;
			if(!in[v])
			{
				cnt[v]++;
				q.push(v);
				in[v]=1;
				if(cnt[v]>=n)
				{
					cout<<"YES"<<'\n';
						return;
				}
			}	
			}
		}	
	}	
	cout<<"NO"<<'\n';
}
int main()
{
	cin>>T;
	for (int  t = 0; t < T; t++){
		cin>>n>>m;
		for (int i = 1; i <= n; i++){
			G[i].clear();
		}
		for (int i = 0; i < m; i++){
			cin>>u>>v>>w;
			G[u].push_back(make_pair(v, w));
			if (w >= 0){
				G[v].push_back(make_pair(u, w)); 
			} 
		}
		spfa();
	}
	return 0;
}

【模板】差分约束

题目描述

给出一组包含 \(m\) 个不等式，有 \(n\) 个未知数的形如：

\[ \begin{cases} x_{c_1}-x_{c'_1}\leq y_1 \\x_{c_2}-x_{c'_2} \leq y_2 \\ \cdots\\ x_{c_m} - x_{c'_m}\leq y_m\end{cases}\]

的不等式组，求任意一组满足这个不等式组的解。

输入格式

第一行为两个正整数 \(n,m\)，代表未知数的数量和不等式的数量。

接下来 \(m\) 行，每行包含三个整数 \(c,c',y\)，代表一个不等式 \(x_c-x_{c'}\leq y\)。

输出格式

一行，\(n\) 个数，表示 \(x_1 , x_2 \cdots x_n\) 的一组可行解，如果有多组解，请输出任意一组，无解请输出 NO。

样例 #1

样例输入 #1

3 3
1 2 3
2 3 -2
1 3 1

样例输出 #1

5 3 5

提示

样例解释

\(\begin{cases}x_1-x_2\leq 3 \\ x_2 - x_3 \leq -2 \\ x_1 - x_3 \leq 1 \end{cases}\)

一种可行的方法是 \(x_1 = 5, x_2 = 3, x_3 = 5\)。

\(\begin{cases}5-3 = 2\leq 3 \\ 3 - 5 = -2 \leq -2 \\ 5 - 5 = 0\leq 1 \end{cases}\)

数据范围

对于 \(100\%\) 的数据，\(1\leq n,m \leq 5\times 10^3\)，\(-10^4\leq y\leq 10^4\)，\(1\leq c,c'\leq n\)，\(c \neq c'\)。

评分策略

你的答案符合该不等式组即可得分，请确保你的答案中的数据在 int 范围内。

如果并没有答案，而你的程序给出了答案，SPJ 会给出 There is no answer, but you gave it，结果为 WA；
如果并没有答案，而你的程序输出了 NO，SPJ 会给出 No answer，结果为 AC；
如果存在答案，而你的答案错误，SPJ 会给出 Wrong answer，结果为 WA；
如果存在答案，且你的答案正确，SPJ 会给出 The answer is correct，结果为 AC。

差分约束问题是一种特殊的N元一次不等式

image-20240229135620747

诸如此类，我们将此变形，实际上可以总结为

image-20240229135645732

这实际上和图论及其相似，可以看成从j出发向i连一条长度为C_K的有向边，然后方程的一组解就是最短路径

先将每个不等式 x i < = x j + c 转化为一条从 j 走到 i ，长度为c的一条边 找一个超级源点（或者建立一个虚拟源点），使得该源点一定可以遍历到所有边 从源点求一遍单源最短路 结果1：如果存在负环，则原不等式组一定无解 结果2：如果没有负环，则dist[i]就是原不等式组的一个可行解。

#include<bits/stdc++.h>
using namespace std;
int n,m;
int cnt;
const int N=5005;
int dis[N];
bool vis[N];
int num[N];
struct edge
{
	int to, w,next;
}e[2*N];
int head[N];
queue<int>q;
void add(int u,int v,int w)
{
	e[++cnt].to=v;
	e[cnt].w=w;
	e[cnt].next=head[u];
	head[u]=cnt;
}
//链式前向星
bool spfa(int x)
{
	dis[x]=0;
	q.push(x);
	vis[x]=1;
	num[x]++;
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		vis[u]=0;
		for(int i=head[u];i!=0;i=e[i].next)
		{
			if(dis[e[i].to]>dis[u]+e[i].w)
			{
				dis[e[i].to]=dis[u]+e[i].w;
				if(!vis[e[i].to])
				{
					q.push(e[i].to);
					vis[e[i].to]=1;
					num[e[i].to]++;
					if(num[e[i].to]==n+1)
					{
						return 0;
					}
					//判负环				
				}
			}
		}
		
	}
	return 1;
}
//spfa模板
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		dis[i]=1e9;
	}
	for(int i=1;i<=m;i++)
	{
		int u,v,w;
		cin>>u>>v>>w;
		add(v,u,w);
	}
    //存边
	for(int i=1;i<=n;i++)
	{
		add(n+1,i,0);
	}
    //建立一个超级原点，保证每个点可以走到
		if(!spfa(n+1))C++
		{
			cout<<"NO"<<'\n';
			return 0;
		}
	for(int i=1;i<=n;i++)
	{
		cout<<dis[i]<<" ";
	}
	
	
}

[USACO06NOV] Roadblocks G

题面翻译

贝茜把家搬到了一个小农场，但她常常回到 FJ 的农场去拜访她的朋友。贝茜很喜欢路边的风景，不想那么快地结束她的旅途，于是她每次回农场，都会选择第二短的路径，而不象我们所习惯的那样，选择最短路。
贝茜所在的乡村有 \(R(1\le R \le 10^5)\) 条双向道路，每条路都联结了所有的 \(N(1\le N\le 5000)\) 个农场中的某两个。贝茜居住在农场 \(1\)，她的朋友们居住在农场 \(N\)（即贝茜每次旅行的目的地）。
贝茜选择的第二短的路径中，可以包含任何一条在最短路中出现的道路，并且，一条路可以重复走多次。当然咯，第二短路的长度必须严格大于最短路（可能有多条）的长度，但它的长度必须不大于所有除最短路外的路径的长度。

题目描述

Bessie has moved to a small farm and sometimes enjoys returning to visit one of her best friends. She does not want to get to her old home too quickly, because she likes the scenery along the way. She has decided to take the second-shortest rather than the shortest path. She knows there must be some second-shortest path.

The countryside consists of R (1 ≤ R ≤ 100,000) bidirectional roads, each linking two of the N (1 ≤ N ≤ 5000) intersections, conveniently numbered 1..N. Bessie starts at intersection 1, and her friend (the destination) is at intersection N.

The second-shortest path may share roads with any of the shortest paths, and it may backtrack i.e., use the same road or intersection more than once. The second-shortest path is the shortest path whose length is longer than the shortest path(s) (i.e., if two or more shortest paths exist, the second-shortest path is the one whose length is longer than those but no longer than any other path).

输入格式

Line 1: Two space-separated integers: N and R

Lines 2..R+1: Each line contains three space-separated integers: A, B, and D that describe a road that connects intersections A and B and has length D (1 ≤ D ≤ 5000)

输出格式

Line 1: The length of the second shortest path between node 1 and node N

样例 #1

样例输入 #1

4 4
1 2 100
2 4 200
2 3 250
3 4 100

样例输出 #1

450

提示

Two routes: 1 -> 2 -> 4 (length 100+200=300) and 1 -> 2 -> 3 -> 4 (length 100+250+100=450)

次短路模板题，有解

继续spfa

#include<bits/stdc++.h>
using namespace std;
const int N=200010;
int cnt;
int n,m,head[N], vis[N],d[5010][2];
//d数组的含义
//0为最短
//1为次短
struct 
{
	int to,w,next;
}e[N];
queue<int>q;
void add(int u,int v,int w)
{
	e[++cnt].to=v;
	e[cnt].w=w;
	e[cnt].next=head[u];
	head[u]=cnt;
}
void spfa(int s)
{
	vis[s]=1;
	d[s][0]=0;
	q.push(s);
	while(!q.empty())
{
	int  u=q.front();
	vis[u]=0;
	q.pop();
	for(int i=head[u];i;i=e[i].next)
	{
		int v=e[i].to;
		if(d[v][0]>d[u][0]+e[i].w)
		{
			d[v][1]=d[v][0];
			d[v][0]=d[u][0]+e[i].w;
		if(!vis[v])
		{
			vis[v]=1;
			q.push(v);
			}	
		}
		if(d[v][1]>d[u][0]+e[i].w&&d[u][0]+e[i].w>d[v][0])
		{
			d[v][1]=d[u][0]+e[i].w;
				if(!vis[v])
		{
			vis[v]=1;
			q.push(v);
			}	
		}
		if(d[v][1]>d[u][1]+e[i].w)
		{
			d[v][1]=d[u][1]+e[i].w;
				if(!vis[v])
		{
			vis[v]=1;
			q.push(v);
			}	
		}		
	}		
}	
}
int main()
{
	memset(d,0x7f7f7f,sizeof(d));
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		int u,v,w;
		cin>>u>>v>>w;
		add(u,v,w);
		add(v,u,w);
		}	
		spfa(n);
		cout<<d[1][1];
}

[USACO08OPEN] Clear And Present Danger S

题面翻译

农夫约翰正驾驶一条小艇在牛勒比海上航行．

海上有 \(N(1\leq N\leq 100)\) 个岛屿，用 \(1\) 到 \(N\) 编号．约翰从 \(1\) 号小岛出发，最后到达 \(N\) 号小岛．

一张藏宝图上说，如果他的路程上经过的小岛依次出现了 \(A_1,A_2,\dots ,A_M(2\leq M\leq 10000)\) 这样的序列（不一定相邻），那他最终就能找到古老的宝藏． 但是，由于牛勒比海有海盗出没．约翰知道任意两个岛屿之间的航线上海盗出没的概率，他用一个危险指数 \(D_{i,j}(0\leq D_{i,j}\leq 100000)\) 来描述．他希望他的寻宝活动经过的航线危险指数之和最小．那么，在找到宝藏的前提下，这个最小的危险指数是多少呢？

输入输出格式

输入格式：

第一行：两个用空格隔开的正整数 \(N\) 和 \(M\)。

第二到第 \(M+1\) 行：第 \(i+1\) 行用一个整数 \(A_i\) 表示 FJ 必须经过的第 \(i\) 个岛屿

第 \(M+2\) 到第 \(N+M+1\) 行：第 \(i+M+1\) 行包含 \(N\) 个用空格隔开的非负整数分别表示 \(i\) 号小岛到第 \(1\dots N\) 号小岛的航线各自的危险指数。保证第 \(i\) 个数是 \(0\)。

输出格式 第一行：FJ 在找到宝藏的前提下经过的航线的危险指数之和的最小值。

说明 这组数据中有三个岛屿，藏宝图要求 FJ 按顺序经过四个岛屿：\(1\) 号岛屿、\(2\) 号岛屿、回到 \(1\) 号岛屿、最后到 \(3\) 号岛屿。每条航线的危险指数也给出了：航路\((1,2),(2,3),(3,1)\) 和它们的反向路径的危险指数分别是 \(5,2,1\)。

FJ 可以通过依次经过 \(1,3,2,3,1,3\) 号岛屿以 \(7\) 的最小总危险指数获得宝藏。这条道路满足了奶牛地图的要求 \((1,2,1,3)\)。我们避开了 \(1\) 号和 \(2\) 号岛屿之间的航线，因为它的危险指数太大了。

注意：测试数据中 \(a\) 到 \(b\) 的危险指数不一定等于 \(b\) 到 \(a\) 的危险指数！

Translated by @LJC00125

题目描述

Farmer John is on a boat seeking fabled treasure on one of the N (1 <= N <= 100) islands conveniently labeled 1..N in the Cowribbean Sea.

The treasure map tells him that he must travel through a certain sequence A_1, A_2, ..., A_M of M (2 <= M <= 10,000) islands, starting on island 1 and ending on island N before the treasure will appear to him. He can visit these and other islands out of order and even more than once, but his trip must include the A_i sequence in the order specified by the map.

FJ wants to avoid pirates and knows the pirate-danger rating (0 <= danger <= 100,000) between each pair of islands. The total danger rating of his mission is the sum of the danger ratings of all the paths he traverses.

Help Farmer John find the least dangerous route to the treasure that satisfies the treasure map's requirement.

输入格式

* Line 1: Two space-separated integers: N and M

* Lines 2..M+1: Line i+1 describes the i_th island FJ must visit with a single integer: A_i

* Lines M+2..N+M+1: Line i+M+1 contains N space-separated integers that are the respective danger rating of the path between island i and islands 1, 2, ..., and N, respectively. The ith integer is always zero.

输出格式

* Line 1: The minimum danger that Farmer John can encounter while obtaining the treasure.

样例 #1

样例输入 #1

3 4 
1 
2 
1 
3 
0 5 1 
5 0 2 
1 2 0

样例输出 #1

7

提示

There are 3 islands and the treasure map requires Farmer John to visit a sequence of 4 islands in order: island 1, island 2, island 1 again, and finally island 3. The danger ratings of the paths are given: the paths (1, 2); (2, 3); (3, 1) and the reverse paths have danger ratings of 5, 2, and 1, respectively.

He can get the treasure with a total danger of 7 by traveling in the sequence of islands 1, 3, 2, 3, 1, and 3. The cow map's requirement (1, 2, 1, and 3) is satisfied by this route. We avoid the path between islands 1 and 2 because it has a large danger rating.

输入输出格式

输入格式：

第一行：两个用空格隔开的正整数N和M

第二到第M+1行：第i+1行用一个整数Ai表示FJ必须经过的第i个岛屿

第M+2到第N+M+1行：第i+M+1行包含N个用空格隔开的非负整数分别表示i号小岛到第1...N号小岛的航线各自的危险指数。保证第i个数是0。

输出格式

第一行：FJ在找到宝藏的前提下经过的航线的危险指数之和的最小值。

说明

这组数据中有三个岛屿，藏宝图要求FJ按顺序经过四个岛屿：1号岛屿、2号岛屿、回到1号岛屿、最后到3号岛屿。每条航线的危险指数也给出了：航路(1，2)、(2，3)、(3，1)和它们的反向路径的危险指数分别是5、2、1。

FJ可以通过依次经过1、3、2、3、1、3号岛屿以7的最小总危险指数获得宝藏。这条道路满足了奶牛地图的要求（1，2，1，3）。我们避开了1号和2号岛屿之间的航线，因为它的危险指数太大了。

注意：测试数据中a到b的危险指数不一定等于b到a的危险指数！

弗洛伊德模板：因为数据范围很小

for(int k=1;k<=n;k++)
	{
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				dis[i][j]=min(dis[i][k]+dis[k][j],dis[i][j]);//松弛
			}
		}
	}

#include<bits/stdc++.h>
using namespace std;
int a[1000][1000];
int n,m;
int b[1000000];
void floyd()
{
	for(int k=1;k<=n;k++)
	{		
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				a[i][j]=min(a[i][j],a[i][k]+a[k][j]);
			}
		}	
	}	
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		cin>>b[i];	
	}
	memset(a,0x3f3f3f,sizeof(a));	
	for(int i=1;i<=n;i++)
	{
	for(int j=1;j<=n;j++)
	{
		int v;
		cin>>v;
		a[i][j]=v;
	}	
	}
	floyd();
	int sum=0;
	for(int i=2;i<=m;i++)
	{
		sum+=a[b[i-1]][b[i]];
			
	}
	cout<<sum;	
}

【模板】传递闭包

题目描述

给定一张点数为 \(n\) 的有向图的邻接矩阵，图中不包含自环，求该有向图的传递闭包。

一张图的邻接矩阵定义为一个 \(n\times n\) 的矩阵 \(A=(a_{ij})_{n\times n}\)，其中

\[ a_{ij}=\left\{ \begin{aligned} 1,i\ 到\ j\ 存在直接连边\\ 0,i\ 到\ j\ 没有直接连边 \\ \end{aligned} \right. \] 一张图的传递闭包定义为一个 \(n\times n\) 的矩阵 \(B=(b_{ij})_{n\times n}\)，其中

\[ b_{ij}=\left\{ \begin{aligned} 1,i\ 可以直接或间接到达\ j\\ 0,i\ 无法直接或间接到达\ j\\ \end{aligned} \right. \]

输入格式

输入数据共 \(n+1\) 行。

第一行一个正整数 \(n\)。

第 \(2\) 到 \(n+1\) 行每行 \(n\) 个整数，第 \(i+1\) 行第 \(j\) 列的整数为 \(a_{ij}\)。

输出格式

输出数据共 \(n\) 行。

第 \(1\) 到 \(n\) 行每行 \(n\) 个整数，第 \(i\) 行第 \(j\) 列的整数为 \(b_{ij}\)。

样例 #1

样例输入 #1

4
0 0 0 1
1 0 0 0
0 0 0 1
0 1 0 0

样例输出 #1

1 1 0 1
1 1 0 1
1 1 0 1
1 1 0 1

提示

对于 \(100\%\) 的数据，\(1\le n\le 100\)，保证 \(a_{ij}\in\{0,1\}\) 且 \(a_{ii}=0\)。

#include<bits/stdc++.h>
using namespace std;
int d[110][110],n;
int main(){
	cin>>n;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			cin>>d[i][j];
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				d[i][j]=max(d[i][j],min(d[i][k],d[k][j]));
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++)
			cout<<d[i][j]<<" ";
		cout<<'\n';
	}
}

最短路计数

题目描述

给出一个 \(N\) 个顶点 \(M\) 条边的无向无权图，顶点编号为 \(1\sim N\)。问从顶点 \(1\) 开始，到其他每个点的最短路有几条。

输入格式

第一行包含 \(2\) 个正整数 \(N,M\)，为图的顶点数与边数。

接下来 \(M\) 行，每行 \(2\) 个正整数 \(x,y\)，表示有一条连接顶点 \(x\) 和顶点 \(y\) 的边，请注意可能有自环与重边。

输出格式

共 \(N\) 行，每行一个非负整数，第 \(i\) 行输出从顶点 \(1\) 到顶点 \(i\) 有多少条不同的最短路，由于答案有可能会很大，你只需要输出 $ ans $ 后的结果即可。如果无法到达顶点 \(i\) 则输出 \(0\)。

样例 #1

样例输入 #1

5 7
1 2
1 3
2 4
3 4
2 3
4 5
4 5

样例输出 #1

1
1
1
2
4

提示

\(1\) 到 \(5\) 的最短路有 \(4\) 条，分别为 \(2\) 条 \(1\to 2\to 4\to 5\) 和 \(2\) 条 \(1\to 3\to 4\to 5\)（由于 \(4\to 5\) 的边有 \(2\) 条）。

对于 \(20\%\) 的数据，\(1\le N \le 100\)；
对于 \(60\%\) 的数据，\(1\le N \le 10^3\)；
对于 \(100\%\) 的数据，\(1\le N\le10^6\)，\(1\le M\le 2\times 10^6\)。

#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<queue>
#include<iostream>
using namespace std;
const int maxn=1000000+1,maxm=2000000+1,INF=0x7f7f7f7f,MOD=100003;
vector<int>G[maxn];int dep[maxn];bool vis[maxn];int cnt[maxn];

int main(){
    int N,M;
    cin>>N>>M;
    for(int i=1;i<=M;i++){
        int x,y;
        cin>>x>>y;
        G[x].push_back(y);
        G[y].push_back(x);
    }
    queue<int>Q;
    dep[1]=0;
    vis[1]=1;
    Q.push(1);
    cnt[1]=1;
    while(!Q.empty())
    {
        int x=Q.front();Q.pop();
        for(int i=0;i<G[x].size();i++)
        {
            int t=G[x][i];
            if(!vis[t]){vis[t]=1;dep[t]=dep[x]+1;Q.push(t);}
            //如果这个点的最短路可以更新但还未被更新既
            if(dep[t]==dep[x]+1){cnt[t]=(cnt[t]+cnt[x])%MOD;}
            //方案计数
        }
    }
    for(int i=1;i<=N;i++){
        cout<<cnt[i]<<'\n';
    }
   
}

佳佳的魔法药水

题目背景

发完了 \(k\) 张照片，佳佳却得到了一个坏消息：他的 MM 得病了！佳佳和大家一样焦急万分！治好 MM 的病只有一种办法，那就是传说中的 \(0\) 号药水…… 怎么样才能得到 \(0\) 号药水呢？你要知道佳佳的家境也不是很好，成本得足够低才行……

题目描述

存在 ab 相同 c 不同的情况，与题意相悖。题还是可以做，但数据待修正。

得到一种药水有两种方法：可以按照魔法书上的指导自己配置，也可以到魔法商店里去买——那里对于每种药水都有供应，虽然有可能价格很贵。在魔法书上有很多这样的记载：

\(1\) 份 A 药水混合 \(1\) 份 B 药水就可以得到 \(1\) 份 C 药水。（至于为什么 \(1 + 1 = 1\)，因为……这是魔法世界）好了，现在你知道了需要得到某种药水，还知道所有可能涉及到的药水的价格以及魔法书上所有的配置方法，现在要问的就是：

1. 最少花多少钱可以配制成功这种珍贵的药水；

2. 共有多少种不同的花费最少的方案（两种可行的配置方案如果有任何一个步骤不同则视为不同的）。假定初始时你手中并没有任何可以用的药水。

输入格式

第一行有一个整数 \(N\)（\(N \le 1000\)），表示一共涉及到的药水总数。药水从 \(0 \sim N-1\) 顺序编号，\(0\) 号药水就是最终要配制的药水。

第二行有 \(N\) 个整数，分别表示从 \(0 \sim N-1\) 顺序编号的所有药水在魔法商店的价格（都表示 \(1\) 份的价格）。

第三行开始，每行有三个整数 A、B、C，表示 \(1\) 份 A 药水混合 \(1\) 份 B 药水就可以得到 \(1\) 份 C 药水。注意，某两种特定的药水搭配如果能配成新药水的话，那么结果是唯一的。也就是说不会出现某两行的 A、B 相同但 C 不同的情况。

输入以一个空行结束。

输出格式

输出两个用空格隔开的整数，分别表示得到 \(0\) 号药水的最小花费以及花费最少的方案的个数。

保证方案数不超过 \(2^{63} - 1\)。

样例 #1

样例输入 #1

7 
10 5 6 3 2 2 3 
1 2 0 
4 5 1 
3 6 2

样例输出 #1

10 3

提示

数据范围：

每一种药水的价格均 \(\ge 1\) 且 \(\le 2.8\times 10^4\)。

样例说明：

最优方案有 \(3\) 种，分别是：

• 直接买 \(0\) 号药水；
• 买 \(4\) 号药水、\(5\) 号药水配制成 \(1\) 号药水，直接买 \(2\) 号药水，然后配制成 \(0\) 号药水；
• 买 \(4\) 号药水、\(5\) 号药水配制成 \(1\) 号药水，买 \(3\) 号药水、\(6\) 号药水配制成 \(2\) 号药水，然后配制成 \(0\) 号药水。

• 每次找一个值最小但却没有确定最小值的药水，将其标记为最小值，然后枚举能与此药水合成药水的药水，用找到的药水与配对的药水更新合成药水的最小值

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=1000001;
struct  
{
    int u,v,next;
}e[N];
//链式前向星
int tot=0;
int head[N];
void add(int u,int v,int w)
{
    e[++tot].u=v;
    e[tot].v=w;
    e[tot].next=head[u];
    head[u]=tot;
}
//注意要记录合成的那条边，是u，v是变成的那条
struct P
{
    int huafei;
    int fangan;
    bool flag;
}a[N];
//花费，方案，以及是否找到过的记录
typedef pair<int,int> PII;
priority_queue<PII,vector<PII>,greater<PII>  >q;
//堆
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
    cin>>a[i].huafei;
    a[i].fangan=1;
    q.push({a[i].huafei,i});
}
//输入花费，方案为1
int u,v,w;
while(cin>>u>>v>>w)
{
add(u,v,w);
//两瓶相同的药是可以混成一瓶新药的，即A+A=C。
//需要特判一下
//避免多存
if(u==v)
{
    continue;
}
add(v,u,w);
//反向建一条边
}
while(!q.empty())
{
int c=q.top().first,u=q.top().second;
q.pop();
if(c!=a[u].huafei)
{
    continue;
}
//
a[u].flag=1;
for(int i=head[u];i;i=e[i].next)
{
int x=e[i].u;
int v=e[i].v;
//要用的边
//要到的边
if(a[x].flag)
{
    //如果要用的边有标记过
if(a[v].huafei>c+a[x].huafei)
{
    a[v].huafei=c+a[x].huafei;
    a[v].fangan=a[u].fangan*a[x].fangan;
    q.push({a[v].huafei,v});
}
    //更新最小，花费加，方案乘法
else if(a[v].huafei==c+a[x].huafei)
{
    a[v].fangan+=a[u].fangan*a[x].fangan;
    //相同需要加方案
}
}
}
}
cout<<a[0].huafei<<' '<<a[0].fangan;
}

通往奥格瑞玛的道路

题目背景

在艾泽拉斯大陆上有一位名叫歪嘴哦的神奇术士，他是部落的中坚力量。

有一天他醒来后发现自己居然到了联盟的主城暴风城。

在被众多联盟的士兵攻击后，他决定逃回自己的家乡奥格瑞玛。

题目描述

在艾泽拉斯，有 \(n\) 个城市。编号为 \(1,2,3,\ldots,n\)。

城市之间有 \(m\) 条双向的公路，连接着两个城市，从某个城市到另一个城市，会遭到联盟的攻击，进而损失一定的血量。

每次经过一个城市，都会被收取一定的过路费（包括起点和终点）。路上并没有收费站。

假设 \(1\) 为暴风城，\(n\) 为奥格瑞玛，而他的血量最多为 \(b\)，出发时他的血量是满的。如果他的血量降低至负数，则他就无法到达奥格瑞玛。

歪嘴哦不希望花很多钱，他想知道，在可以到达奥格瑞玛的情况下，他所经过的所有城市中最多的一次收取的费用的最小值是多少。

输入格式

第一行 \(3\) 个正整数，\(n,m,b\)。分别表示有 \(n\) 个城市，\(m\) 条公路，歪嘴哦的血量为 \(b\)。

接下来有 \(n\) 行，每行 \(1\) 个正整数，\(f_i\)。表示经过城市 \(i\)，需要交费 \(f_i\) 元。

再接下来有 \(m\) 行，每行 \(3\) 个正整数，\(a_i,b_i,c_i\)（\(1\leq a_i,b_i\leq n\)）。表示城市 \(a_i\) 和城市 \(b_i\) 之间有一条公路，如果从城市 \(a_i\) 到城市 \(b_i\)，或者从城市 \(b_i\) 到城市 \(a_i\)，会损失 \(c_i\) 的血量。

输出格式

仅一个整数，表示歪嘴哦交费最多的一次的最小值。

如果他无法到达奥格瑞玛，输出 AFK。

样例 #1

样例输入 #1

4 4 8
8
5
6
10
2 1 2
2 4 1
1 3 4
3 4 3

样例输出 #1

10

提示

对于 \(60\%\) 的数据，满足 \(n\leq 200\)，\(m\leq 10^4\)，\(b\leq 200\)；

对于 \(100\%\) 的数据，满足 \(1\leq n\leq 10^4\)，\(1\leq m\leq 5\times 10^4\)，\(1\leq b\leq 10^9\)；

对于 \(100\%\) 的数据，满足 \(1\leq c_i\leq 10^9\)，\(1\leq f_i\leq 10^9\)，可能有两条边连接着相同的城市。

求出到达路线中最大收费的最小值

我们假设需要的钱越多，能走的点也就越多，可以走到终点的可能性也就越大，因此可以二分

//二分枚举答案判断能不能走
//最短路dj优化
//最大值提前走，判断能不能走
#include<bits/stdc++.h>
#define N 10005
#define M 100005
#define MAXN 1000000005 
using namespace std;
int f[N];
bool ed[N];
int dis[N];
int head[N];
priority_queue <pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > que;
int n,m,b;
int t;
struct edge
{
	int to,next,len;
}e[M];
void add(int x,int y,int z)
{
	e[++t].len=z;
	e[t].to=y;
	e[t].next=head[x];
	head[x]=t;
}
bool work(int x)
{
   if(x<f[1])
   return 0;
	for(int i=1;i<=n;i++)
	{
		dis[i]=1e9;
	}
	memset(ed,0,sizeof(ed));
	dis[1]=0;
	que.push(make_pair(0,1));
	int s1,s2;
	while(que.size()){
		s1=que.top().second;que.pop();
		if(ed[s1])continue;
		ed[s1]=1;
		s2=head[s1];
		while(s2)
		{
			if(f[e[s2].to]<=x&&ed[e[s2].to]==0&&dis[s1]+e[s2].len<dis[e[s2].to])
			{
             dis[e[s2].to]=dis[s1]+e[s2].len;
			que.push(make_pair(dis[e[s2].to],e[s2].to));
            }
			s2=e[s2].next;//去下一条边 
		}
	}
	if(dis[n]<=b)
    {
		return 1;
	}
	return 0;
}
int main()
{
	cin>>n>>m>>b;
	for( int i=1;i<=n;i++)
	cin>>f[i];//储存费用
	int a1,a2,a3;
	for( int i=1;i<=m;i++){
		cin>>a1>>a2>>a3;
		if(a1==a2)
		{
			continue;
		}
		add(a1,a2,a3);
		add(a2,a1,a3);
	}
	if(work(MAXN)==0)
	{
		cout<<"AFK";
		return 0;
	} 
	int l=1,r=MAXN,mid=(l+r)>>1;//二分
 	int c;
 	while(l<=r){
 		c=work(mid);
 		if(c){//如果可以的话 
 			r=mid-1;
 			mid=(l+r)>>1;
		 }
 		else{
 			l=mid+1;
 			mid=(l+r)>>1;
		 }
	 }
	 cout<<l<<endl;
}

[NOIP2009 提高组] 最优贸易

题目描述

\(C\) 国有 \(n\) 个大城市和 \(m\) 条道路，每条道路连接这 \(n\) 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 \(m\) 条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为 \(1\) 条。

\(C\) 国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到 \(C\) 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设 \(C\) 国 \(n\) 个城市的标号从 \(1\sim n\)，阿龙决定从 \(1\) 号城市出发，并最终在 \(n\) 号城市结束自己的旅行。在旅游的过程中，任何城市可以重复经过多次，但不要求经过所有 \(n\) 个城市。阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品――水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来 \(C\) 国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

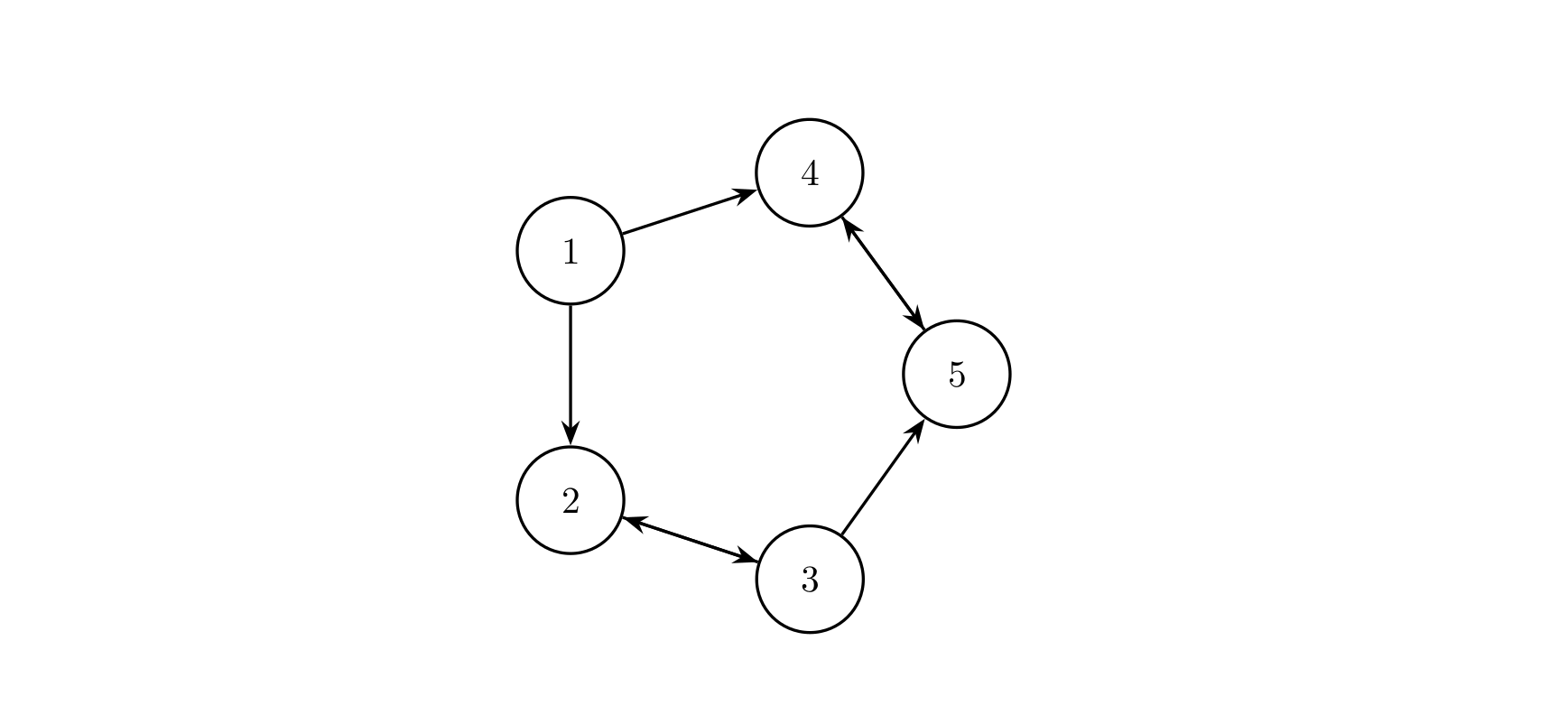
假设 \(C\) 国有 \(5\) 个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路为单向通行，双向箭头表示这条道路为双向通行。

假设 \(1\sim n\) 号城市的水晶球价格分别为 \(4,3,5,6,1\)。

阿龙可以选择如下一条线路：\(1\to2\to3\to5\)，并在 \(2\) 号城市以 \(3\) 的价格买入水晶球，在 \(3\) 号城市以 \(5\) 的价格卖出水晶球，赚取的旅费数为 \(2\)。

阿龙也可以选择如下一条线路：\(1\to4\to5\to4\to5\)，并在第 \(1\) 次到达 \(5\) 号城市时以 \(1\) 的价格买入水晶球，在第 \(2\) 次到达 \(4\) 号城市时以 \(6\) 的价格卖出水晶球，赚取的旅费数为 \(5\)。

现在给出 \(n\) 个城市的水晶球价格，\(m\) 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

输入格式

第一行包含 \(2\) 个正整数 \(n\) 和 \(m\)，中间用一个空格隔开，分别表示城市的数目和道路的数目。

第二行 \(n\) 个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这 \(n\) 个城市的商品价格。

接下来 \(m\) 行，每行有 \(3\) 个正整数 \(x,y,z\)，每两个整数之间用一个空格隔开。如果 \(z=1\)，表示这条道路是城市 \(x\) 到城市 \(y\) 之间的单向道路；如果 \(z=2\)，表示这条道路为城市 \(x\) 和城市 \(y\) 之间的双向道路。

输出格式

一个整数，表示最多能赚取的旅费。如果没有进行贸易，则输出 \(0\)。

样例 #1

样例输入 #1

5 5 
4 3 5 6 1 
1 2 1 
1 4 1 
2 3 2 
3 5 1 
4 5 2

样例输出 #1

5

提示

【数据范围】

输入数据保证 \(1\) 号城市可以到达 \(n\) 号城市。

对于 \(10\%\) 的数据，\(1\leq n\leq 6\)。

对于 \(30\%\) 的数据，\(1\leq n\leq 100\)。

对于 \(50\%\) 的数据，不存在一条旅游路线，可以从一个城市出发，再回到这个城市。

对于 \(100\%\) 的数据，\(1\leq n\leq 100000\)，\(1\leq m\leq 500000\)，\(1\leq x,y\leq n\)，\(1\leq z\leq 2\)，$1$ 各城市的编号 \(\leq n\)。

水晶球价格 \(\leq 100\)。

NOIP 2009 提高组 第三题

借鉴一下洛谷一位大神的图

img

本题需要建立诸如此类的分层图，并通过spfa求解最长路

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=1e5+10;
int n,m;
int d[N*3];
int in[N*3];
vector<pair<int,int> >G[N*3];
void spfa(int s)
{
for(int i=1;i<=3*n;i++)
{
    d[i]=INT_MIN;
}
    //最长路初始化为最小
d[s]=0;
queue<int>q;
in[s]=1;
q.push(s);
while(!q.empty())
{
int x=q.front();
q.pop();
in[x]=0;
for (auto [v, len] : G[x])
    //一种更优的遍历方法
{
    if (d[v] < d[x] + len)
    {
        d[v] = d[x] + len;
        if (!in[v])
        {
            q.push(v);
            in[v] = 1;
        }
    }
}
}
}
int main()
{
     ios_base::sync_with_stdio(0); cin.tie(0); // 加速cin, cout
    cin >> n >> m;
    int v;
    for(int i=1;i<=n;i++)
    {
        cin>>v;
G[i].push_back({1*n+i,-v});
G[1*n+i].push_back({2*n+i,v});
        //上下层分层图建立
    }
//分层图建立
int x,y,z;
for(int i=1;i<=m;i++)
{
    cin>>x>>y>>z;
    G[x].push_back({y,0});
    G[x+n].push_back({y+n,0});
    G[x+2*n].push_back({y+2*n,0});
    //这是左右分层图建立
    //由于是你可以在图上任意走动，因此是0
    if(z == 2)
    {
    G[y].push_back({x,0});
    G[y+n].push_back({x+n,0});
    G[y+2*n].push_back({x+2*n,0});
    }
        //这是左右分层图建立
    //由于是你可以在图上任意走动，因此是0
}
spfa(1);
cout<<d[3*n];
    //输入右下角的最后一个点
}

小 K 的农场

题目描述

小 K 在 MC 里面建立很多很多的农场，总共 \(n\) 个，以至于他自己都忘记了每个农场中种植作物的具体数量了，他只记得一些含糊的信息（共 \(m\) 个），以下列三种形式描述：
- 农场 \(a\) 比农场 \(b\) 至少多种植了 \(c\) 个单位的作物； - 农场 \(a\) 比农场 \(b\) 至多多种植了 \(c\) 个单位的作物； - 农场 \(a\) 与农场 \(b\) 种植的作物数一样多。

但是，由于小 K 的记忆有些偏差，所以他想要知道存不存在一种情况，使得农场的种植作物数量与他记忆中的所有信息吻合。

输入格式

第一行包括两个整数 \(n\) 和 \(m\)，分别表示农场数目和小 K 记忆中的信息数目。

接下来 \(m\) 行：
- 如果每行的第一个数是 \(1\)，接下来有三个整数 \(a,b,c\)，表示农场 \(a\) 比农场 \(b\) 至少多种植了 \(c\) 个单位的作物；
- 如果每行的第一个数是 \(2\)，接下来有三个整数 \(a,b,c\)，表示农场 \(a\) 比农场 \(b\) 至多多种植了 \(c\) 个单位的作物;
- 如果每行的第一个数是 \(3\)，接下来有两个整数 \(a,b\)，表示农场 \(a\) 种植的的数量和 \(b\) 一样多。

输出格式

如果存在某种情况与小 K 的记忆吻合，输出 Yes，否则输出 No。

样例 #1

样例输入 #1

3 3
3 1 2
1 1 3 1
2 2 3 2

样例输出 #1

Yes

提示

对于 \(100\%\) 的数据，保证 \(1 \le n,m,a,b,c \le 5 \times 10^3\)。

为了避免图不连通的情况，我们需要一个超级源点 n+1 ，与点 i 之间连一条边权为 0 的边。

我们将式子转化为差分约束

#include <bits/stdc++.h>
using namespace std;
int n, m, cnt, elast[5005], dis[5005], num[5005];
bool vis[5005];
struct edge 
{
	int to, len, next;
} e[15005];
queue<int> q;
void add (int u, int v, int w) 
{
	e[++cnt].to = v;
	e[cnt].len = w;
	e[cnt].next = elast[u];
	elast[u] = cnt;
}
bool spfa (int x) 
{
	dis[x] = 0;
	q.push(x);
	vis[x] = true;
	num[x]++;
	while (!q.empty()) 
    {
		int u = q.front();
		q.pop();
		vis[u] = false;
		for (int i = elast[u]; i != 0; i = e[i].next)
			if (dis[e[i].to] > dis[u] + e[i].len) {
				dis[e[i].to] = dis[u] + e[i].len;
				if (!vis[e[i].to]) 
                {
					q.push(e[i].to);
					vis[e[i].to] = true;
					num[e[i].to]++;
					if (num[e[i].to] == n + 1)
						return false;
				}
			}
	}
	return true;
}

int main () {
	cin>>n>>m;
	memset(dis, 0x3f3f3f3f, sizeof(dis));
	for (int i = 1; i <= m; i++) {
		int opt;
		cin>>opt;
		switch (opt) 
        {
			case 1: {
				int a, b, c;
				cin>>a>>b>>c;
				add(a, b, -c);
				break;
			}
			case 2: {
				int a, b, c;
				cin>>a>>b>>c;
				add(b, a, c);
				break;
			}
			case 3: {
				int a, b;
				cin>>a>>b;
				add(a, b, 0);
				add(b, a, 0);
				break;
			}
		}
	}
	for (int i = 1; i <= n; i++)
		add(n + 1, i, 0);
	bool flag = spfa(n + 1);
	if (!flag) 
    {
		cout<<"No";
		return 0;
	}
	cout<<"Yes";
	return 0;
}

[SCOI2011] 糖果

题目描述

幼儿园里有 \(N\) 个小朋友，\(\text{lxhgww}\) 老师现在想要给这些小朋友们分配糖果，要求每个小朋友都要分到糖果。但是小朋友们也有嫉妒心，总是会提出一些要求，比如小明不希望小红分到的糖果比他的多，于是在分配糖果的时候，\(\text{lxhgww}\) 需要满足小朋友们的 \(K\) 个要求。幼儿园的糖果总是有限的，\(\text{lxhgww}\) 想知道他至少需要准备多少个糖果，才能使得每个小朋友都能够分到糖果，并且满足小朋友们所有的要求。

输入格式

输入的第一行是两个整数 \(N\)，\(K\)。接下来 \(K\) 行，表示这些点需要满足的关系，每行 \(3\) 个数字，\(X\)，\(A\)，\(B\)。

• 如果 \(X=1\)， 表示第 \(A\) 个小朋友分到的糖果必须和第 \(B\) 个小朋友分到的糖果一样多；
• 如果 \(X=2\)， 表示第 \(A\) 个小朋友分到的糖果必须少于第 \(B\) 个小朋友分到的糖果；
• 如果 \(X=3\)， 表示第 \(A\) 个小朋友分到的糖果必须不少于第 \(B\) 个小朋友分到的糖果；
• 如果 \(X=4\)， 表示第 \(A\) 个小朋友分到的糖果必须多于第 \(B\) 个小朋友分到的糖果；
• 如果 \(X=5\)， 表示第 \(A\) 个小朋友分到的糖果必须不多于第 \(B\) 个小朋友分到的糖果；

输出格式

输出一行，表示 \(\text{lxhgww}\) 老师至少需要准备的糖果数，如果不能满足小朋友们的所有要求，就输出 \(-1\)。

样例 #1

样例输入 #1

5 7
1 1 2
2 3 2
4 4 1
3 4 5
5 4 5
2 3 5
4 5 1

样例输出 #1

11

提示

对于 \(30\%\) 的数据，保证 \(N\leq100\)

对于 \(100\%\) 的数据，保证 \(N\leq100000\)

对于所有的数据，保证 \(K\leq100000, 1\leq X\leq5, 1\leq A, B\leq N\)

---

\(\text{upd 2022.7.6}\)：新添加 \(21\) 组 Hack 数据。

一份100分的代码，但是hack。

SPFA优化：

Small Label First 优化（小标签优先）。用双端队列 deque 实现，常用。

就是更新完之后比较其 dis 值与 dis[q.front()]的大小，如果较小则放前面，反之放后面。

原理就是 dis 值小的更容易更新其他节点的 dis

每一个小朋友分到的糖果数量不能为零，所以建立汇点连边时边权不再为 0，而是 1。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 4e5 + 5;
int n, m, vis[MAXN], cnt, s, t, head[MAXN];
ll dis[MAXN], ans;
struct edge
{
    int to, nxt, w;
} e[MAXN];
void add(int u, int v, int w)
{
    e[++cnt].to = v;
    e[cnt].nxt = head[u];
    e[cnt].w = w;
    head[u] = cnt;
}
deque<int> q; // 将普通队列进阶为双端队列
void Spfa()
{
    dis[0] = 0;
    q.push_back(0);
    while (!q.empty())
    {
        int u = q.front();
        q.pop_front();
        for (int i = head[u]; i; i = e[i].nxt)
        {
            int v = e[i].to;
            if (dis[v] < dis[u] + e[i].w)
            { 
                // 最长路来求最小值
                dis[v] = dis[u] + e[i].w;
                vis[v]++;
                if (vis[v] == n)
                {
                   cout<<-1;
                    exit(0);
                }
                // SLF优化
                if (q.size() && dis[q.front()] <= dis[v])
                    q.push_front(v);
                else
                    q.push_back(v);
            }
        }
    }
}
int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    // 取消同步流
    cin>>n>>m;
    for (int i = 1, op, u, v; i <= m; i++)
    {
        cin>>op>>u>>v;
        // 因为该题存在实际意义，改变存边方式，思想相同
        if (op == 1)
        {
            add(u, v, 0);
            add(v, u, 0);
            //A=B
        }
        else if (op == 2)
        {
            if (u == v)
            {
                cout<<-1;
                return  0;
            }
            add(u, v, 1);
            //B≥A+1
        }
        else if (op == 3)
        {
            add(v, u, 0);
            //A≥B
        }
        else if (op == 4)
        {
            if (u == v)
            {
                cout<<-1;
                return  0;
            }
            //A≥B+1
            add(v, u, 1);
        }
        else
        {
            add(u, v, 0);
        }
    }
    for (int i = 1; i <= n; i++)
        add(0, i, 1); // 注意边权为 1
    Spfa();
    for (int i = 1; i <= n; i++)
        ans += dis[i];
    cout<<ans;
    return 0;
}

[传智杯 #2 决赛] 传送门

题目描述

传智专修学院里有 \(n\) 栋教学楼，有 \(m\) 条双向通行道路连接这些教学楼，不存在重边和自环。每条道路都有一定的长度，而且所有教学楼之间都可以直接或者间接的通过道路到达。我们可以很容易的求出这些教学楼之间的最短路。

为了使交通更为顺畅，校方决定在两个教学楼里增设一对传送门。传送门可以将这对教学楼的距离直接缩短为 0。利用传送门，某些教学楼之间的最短路的距离就变短了。

由于预算有限，学校里只能安装一对传送门。但是校长希望尽可能方便学生，使任意两点之间的最短路长度的总和最小。当然啦，从 \(x\) 教学楼到 \(y\) 教学楼的长度和从 \(y\) 教学楼到 \(x\) 教学楼的长度只需要统计一次就可以了。

输入格式

输入第 1 行两个正整数 \(n,m(n\le 100,m\le\frac{1}{2}n(n-1))\)，代表教学楼和道路数量。

接下来 \(m\) 行，每行三个正整数 \(x_i,y_i,w_i(0 <w_i \le 10^4)\)，表示在教学楼 \(x_i\) 和 \(y_i\) 之间，有一条长度为 \(w_i\) 的道路。

输出格式

输出一行，在最优方案下的任意点对的最短道路之和。

样例 #1

样例输入 #1

4 5
1 2 3
1 3 6
2 3 4
2 4 7
3 4 2

样例输出 #1

14

提示

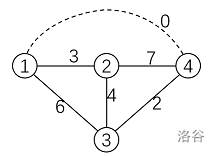
样例如图。当在 1 和 4 号教学楼架设一对传送门时，1 → 2 的最短路是 3，1 → 3 的最短路是 0+2，1 → 4 的最短路是 0，2 → 3 的最短路是 4，2 → 4 的最短路是 3+0，3 → 4 的最短路是 2，最短路之和是 14，是最佳方案。 $$ f[i][j] 表示未建传送门时的

i 到

j 的最短路。

F[i][j] 表示建了传送门之后

i 到

j 的最短路。 $$

#include<bits/stdc++.h>
using namespace std;
const int N=105;
const int INF=1e10;
int a[105][105];
int f[105][105];
int n,m;
int ans;
int sum=INF;
void solve(int i,int j)
{
	int ans=0;
	for(int k=1;k<=n;k++)
	{
		for(int l=1;l<=n;l++)
		{
			f[k][l]=a[k][l];
		}
	}
	f[i][j]=0;
	f[j][i]=0;
    //在教学楼 i 和 j 之间建立传送门
	for(int k=1;k<=n;k++)
	{
		for(int l=1;l<=n;l++)
		{
			f[k][l]=min(f[k][l],f[k][i]+f[i][l]);
		}
	}
		for(int k=1;k<=n;k++)
	{
		for(int l=1;l<=n;l++)
		{
			f[k][l]=min(f[k][l],f[k][j]+f[j][l]);
		}
	}
	for(int k=1;k<=n;k++)
	{
		for(int l=k+1;l<=n;l++)
		{
			ans+=f[k][l];
		}	
	}	
	sum=min(ans,sum);
    //求和
}
int main()
{
	cin>>n>>m;
	memset(a,0x3f,sizeof(a));
for(int i=1; i<=n; i++) a[i][i]=0;
	for(int i=1; i<=m; i++) 
	{
		int x,y,z;
		cin>>x>>y>>z;
		a[x][y]=a[y][x]=z;
	}
	for(int k=1;k<=n;k++)
	{
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				a[i][j]=min(a[i][j],a[i][k]+a[k][j]);			
			}
		}
	}	
    //Floyd算法
for(int i=1;i<=n;i++)
{
	for(int j=i+1;j<=n;j++)
	{
		solve(i,j);
        //枚举
	}
	}	
	cout<<sum;	
}

跳楼机

题目背景

DJL 为了避免成为一只咸鱼，来找 srwudi 学习压代码的技巧。

题目描述

Srwudi 的家是一幢 \(h\) 层的摩天大楼。由于前来学习的蒟蒻越来越多，srwudi 改造了一个跳楼机，使得访客可以更方便的上楼。

经过改造，srwudi 的跳楼机可以采用以下四种方式移动：

1. 向上移动 \(x\) 层；
2. 向上移动 \(y\) 层；
3. 向上移动 \(z\) 层；
4. 回到第一层。

一个月黑风高的大中午，DJL 来到了 srwudi 的家，现在他在 srwudi 家的第一层，碰巧跳楼机也在第一层。DJL 想知道，他可以乘坐跳楼机前往的楼层数。

输入格式

第一行一个整数 \(h\)，表示摩天大楼的层数。

第二行三个正整数，分别表示题目中的 \(x, y, z\)。

输出格式

一行一个整数，表示 DJL 可以到达的楼层数。

样例 #1

样例输入 #1

15
4 7 9

样例输出 #1

9

样例 #2

样例输入 #2

33333333333
99005 99002 100000

样例输出 #2

33302114671

提示

可以到达的楼层有：\(1,5,8,9,10,12,13,14,15\)。

\(1 \le h \le 2^{63}-1\)，\(1 \le x,y,z \le 10^5\)。

%%%昨天看htgg的同余最短路，一头雾水（）

今天就遇到一题，看来是不得不学了）

算法学习笔记(93): 同余最短路 - 知乎 (zhihu.com) \[ 同余最短路 能解决的问题： 给定n个整数，求这n个数能拼凑出多少其他的整数（可重复取）。 \]

\[ 或者求n个整数不能拼出的最大/最小数。 \]

$$ 给定多个形如

a i ​ −a j ​ ≥c ij ​ 的不定式，找出一种可行解。

这种问题有一种很巧妙的构造方法，就是将这类问题抽象成一个图论问题来解决。

具体来说，就是将不等式移项，变为

a i ​ ≥a j ​ +c ij ​ ，发现很像最短（长）路中的式子。

在每条边都松弛完成之后，在最短路中每条边都满足

d y ​ ≤d x ​ +z（不存在负环），反之可以继续松弛。同理，在最长路中每条边都满足

d y ​ ≥d x ​ +z（不存在正环）。

如此，发现和原来的不等式很像，于是连接

j到

i，边权为

c ij ​ 的边，跑一边最长路，就得到了原问题的一种可行解。 $$

image-20240302142943796

image-20240302143046487

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=2e5+10;
const int INf=0x3f3f3f3f;
ll h,x,y,z;
ll f[N];
ll ans;
bool vis[N];
int tot;
struct 
{
    int to,next,w;
}e[N];
int head[N];
void add(int u,int v,int w)
{
e[++tot].to=v;
e[tot].w=w;
e[tot].next=head[u];
head[u]=tot;
}
void spfa()
{
    memset(f,INf,sizeof f);
    memset(vis,0,sizeof vis);
    queue<int> q;
    q.push(1);
    vis[1]=1;
    f[1]=1;
    while(!q.empty())
    {
int x=q.front();
q.pop();
vis[x]=0;
for(int i=head[x];i;i=e[i].next)
{
   int y=e[i].to;
    if(f[y]>f[x]+e[i].w)
    {
        f[y]=f[x]+e[i].w;
        if(!vis[y])
        {
            q.push(y);
            vis[y]=1;
        }
    }
}
    }
}
int main()
{
cin>>h>>x>>y>>z;
if(x==1||y==1||z==1)
{
    cout<<h;
    return 0;
}
for(int i=0;i<x;i++)
{
    add(i,(i+y)%x,y);
    add(i,(i+z)%x,z);
    //添加边，0-(0+y)%x有一条y的边
    //z同理
}
spfa();
for(ll i=0;i<x;i++)
{
    if(f[i]<=h)
    {
        ans+=(h-f[i])/x+1;
        //统计方案数字
        //用高度减去能够到达的最小高度，然后再对x取模，然后+1即可。
    }
}
cout<<ans;
}

提供一位大佬的博客

同余最短路 - 洛谷专栏 (luogu.com)

以及对于的Dijkstra代码

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N=1e5+10,M=2e5+10;

int head[N],ver[M],edge[M],nxt[M],tot=1;
void add(int x,int y,int z){
    ver[++tot]=y,edge[tot]=z,nxt[tot]=head[x],head[x]=tot;
}

ll f[N],ans,h,X,Y,Z;
bool v[N];
priority_queue<pair<ll,int>>q;
void dijkstra(){
    memset(f,0x3f,sizeof(f));
    f[1]=1;q.push({1,1});
    while(q.size()){
        int x=q.top().second;q.pop();
        if(v[x])continue;
        v[x]=1;
        for(int i=head[x];i;i=nxt[i]){
            int y=ver[i];
            if(f[y]>f[x]+edge[i]){
                f[y]=f[x]+edge[i];
                q.push({-f[y],y});
            }
        }
    }
}

int main(){
    scanf("%lld%lld%lld%lld",&h,&X,&Y,&Z);
    if(X==1||Y==1||Z==1)printf("%lld\n",h),exit(0);
    for(int i=0;i<X;i++){
        add(i,(i+Y)%X,Y);
        add(i,(i+Z)%X,Z);
    }
    dijkstra();
    for(int i=0;i<X;i++)
        if(f[i]<=h)ans+=(h-f[i])/X+1;
    printf("%lld\n",ans);
    return 0;
}

还有一题：

[ABC077D] Small Multiple

题面翻译

给定一个整数 \(K\)。求一个 \(K\) 的正整数倍 \(S\)，使得 \(S\) 的数位累加和最小。

【数据范围】

• \(2 \le K \le {10}^5\)；
• \(K\) 是整数。

【输入格式】

一行一个正整数 \(K\)。

【输出格式】

输出 \(K\) 的正整数倍的最小数位累加和。

翻译提供者：Tang_pipi

题目描述

$ K $ の正の倍数の $ 10 $ 進法での各桁の和としてありうる最小の値を求めてください。

输入格式

入力は以下の形式で標準入力から与えられる。

$ K $

输出格式

$ K $ の倍数の $ 10 $ 進法での各桁の和としてありうる最小の値を出力せよ。

样例 #1

样例输入 #1

6

样例输出 #1

3

样例 #2

样例输入 #2

41

样例输出 #2

5

样例 #3

样例输入 #3

79992

样例输出 #3

36

提示

制約

• $ 2  K  10^5 $
• $ K $ は整数である

Sample Explanation 1

$ 12=6×2 $ が最小値を達成します。

Sample Explanation 2

$ 11111=41×271 $ が最小値を達成します。

对于数字 x ，转移有两种：

• 转移到 x+1，各位数字之和 +1。
• 转移到 10x ，各位数字之和不变。

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N=1e5+10,M=2e5+10;

int head[N],ver[M],edge[M],nxt[M],tot=1;
void add(int x,int y,int z){
    ver[++tot]=y,edge[tot]=z,nxt[tot]=head[x],head[x]=tot;
}

ll f[N],n;
bool v[N];
priority_queue<pair<ll,int>>q;
void dijkstra(){
    memset(f,0x3f,sizeof(f));
    f[1]=1;q.push({1,1});
    while(q.size()){
        int x=q.top().second;q.pop();
        if(v[x])continue;
        v[x]=1;
        for(int i=head[x];i;i=nxt[i]){
            int y=ver[i];
            if(f[y]>f[x]+edge[i]){
                f[y]=f[x]+edge[i];
                q.push({-f[y],y});
            }
        }
    }
}

int main(){
   cin>>n;
    for(int i=0;i<n;i++)C++
        add(i,(i+1)%n,1),add(i,(i*10)%n,0);
    dijkstra();
    cout<<f[0];
}

[国家集训队] 墨墨的等式

题目描述

墨墨突然对等式很感兴趣，他正在研究 \(\sum_{i=1}^n a_ix_i=b\) 存在非负整数解的条件，他要求你编写一个程序，给定 \(n, a_{1\dots n}, l, r\)，求出有多少 \(b\in[l,r]\) 可以使等式存在非负整数解。

输入格式

第一行三个整数 \(n,l,r\)。

第二行 \(n\) 个整数 \(a_{1\dots n}\)。

输出格式

一行一个整数，表示有多少 \(b\in[l,r]\) 可以使等式存在非负整数解。

样例 #1

样例输入 #1

2 5 10
3 5

样例输出 #1

5

提示

对于 \(20\%\) 的数据，\(n \le 5\)，\(r \le 10\)。

对于 \(40\%\) 的数据，\(n \le 10\)，\(r \le 10^6\)。

对于 \(100\%\) 的数据，\(n \le 12\)，\(0 \le a_i \le 5\times 10^5\)，\(1 \le l \le r \le 10^{12}\)。

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N=5e5+10,M=6e6+10;
int head[N],ver[M],edge[M],nxt[M],tot=1;
void add(int x,int y,int z)
{
    ver[++tot]=y,edge[tot]=z,nxt[tot]=head[x],head[x]=tot;
}
ll f[N],ans,n,l,r,a[N],m;
bool v[N];
priority_queue<pair<ll,int>>q;
void dijkstra()
{
    memset(f,0x3f,sizeof(f));
    f[0]=0;q.push({0,0});
    while(q.size()){
        int x=q.top().second;q.pop();
        if(v[x])continue;
        v[x]=1;
        for(int i=head[x];i;i=nxt[i])
        {
            int y=ver[i];
            if(f[y]>f[x]+edge[i])
            {
                f[y]=f[x]+edge[i];
                q.push({-f[y],y});
            }
        }
    }
}
ll solve(ll x){
    ll ans=0;
    for(int i=0;i<a[1];i++)
        if(f[i]<=x)ans+=(x-f[i])/a[1]+1;
    return ans;
}
int main()
{
    cin>>n>>l>>r;
    for(int i=1,x;i<=n;i++)
    {
        cin>>x;
        if(x)a[++m]=x;
    }
    for(int i=0;i<a[1];i++)
        for(int j=2;j<=m;j++)
            if(a[j]!=a[1])add(i,(i+a[j])%a[1],a[j]);
    dijkstra();
    cout<<solve(r)-solve(l-1);
    return 0;
}

灾后重建

题目背景

B 地区在地震过后，所有村庄都造成了一定的损毁，而这场地震却没对公路造成什么影响。但是在村庄重建好之前，所有与未重建完成的村庄的公路均无法通车。换句话说，只有连接着两个重建完成的村庄的公路才能通车，只能到达重建完成的村庄。

题目描述

给出 B 地区的村庄数 \(N\)，村庄编号从 \(0\) 到 \(N-1\)，和所有 \(M\) 条公路的长度，公路是双向的。并给出第 \(i\) 个村庄重建完成的时间 \(t_i\)，你可以认为是同时开始重建并在第 \(t_i\) 天重建完成，并且在当天即可通车。若 \(t_i\) 为 \(0\) 则说明地震未对此地区造成损坏，一开始就可以通车。之后有 \(Q\) 个询问 \((x,y,t)\)，对于每个询问你要回答在第 \(t\) 天，从村庄 \(x\) 到村庄 \(y\) 的最短路径长度为多少。如果无法找到从 \(x\) 村庄到 \(y\) 村庄的路径，经过若干个已重建完成的村庄，或者村庄 \(x\) 或村庄 \(y\) 在第 \(t\) 天仍未重建完成，则需要输出 \(-1\)。

输入格式

第一行包含两个正整数 \(N,M\)，表示了村庄的数目与公路的数量。

第二行包含 \(N\) 个非负整数 \(t_0,t_1,\cdots,t_{N-1}\)，表示了每个村庄重建完成的时间，数据保证了 \(t_0 \le t_1 \le \cdots \le t_{N-1}\)。

接下来 \(M\) 行，每行 \(3\) 个非负整数 \(i,j,w\)，\(w\) 不超过 \(10000\)，表示了有一条连接村庄 \(i\) 与村庄 \(j\) 的道路，长度为 \(w\)，保证 \(i\neq j\)，且对于任意一对村庄只会存在一条道路。

接下来一行也就是 \(M+3\) 行包含一个正整数 \(Q\)，表示 \(Q\) 个询问。

接下来 \(Q\) 行，每行 \(3\) 个非负整数 \(x,y,t\)，询问在第 \(t\) 天，从村庄 \(x\) 到村庄 \(y\) 的最短路径长度为多少，数据保证了 \(t\) 是不下降的。

输出格式

共 \(Q\) 行，对每一个询问 \((x,y,t)\) 输出对应的答案，即在第 \(t\) 天，从村庄 \(x\) 到村庄 \(y\) 的最短路径长度为多少。如果在第 \(t\) 天无法找到从 \(x\) 村庄到 \(y\) 村庄的路径，经过若干个已重建完成的村庄，或者村庄 \(x\) 或村庄 \(y\) 在第 \(t\) 天仍未修复完成，则输出 \(-1\)。

样例 #1

样例输入 #1

4 5
1 2 3 4
0 2 1
2 3 1
3 1 2
2 1 4
0 3 5
4
2 0 2
0 1 2
0 1 3
0 1 4

样例输出 #1

-1
-1
5
4

提示

• 对于 \(30\%\) 的数据，有 \(N\le 50\)；
• 对于 \(30\%\) 的数据，有 \(t_i=0\)，其中有 \(20\%\) 的数据有 \(t_i=0\) 且 \(N>50\)；
• 对于 \(50\%\) 的数据，有 \(Q\le 100\)；
• 对于 \(100\%\) 的数据，有 \(1\le N\le 200\)，\(0\le M\le \dfrac{N\times(N-1)}{2}\)，\(1\le Q\le 50000\)，所有输入数据涉及整数均不超过 \(10^5\)。

#include<iostream>
#define N 2050
using namespace std;
int n,m;
int a[N];
int f[N][N];
//邻接矩阵存边
inline void updata(int k)
{
	for(int i=0;i<n;i++)
	for(int j=0;j<n;j++)
	if(f[i][j]>f[i][k]+f[j][k])
	f[i][j]=f[j][i]=f[i][k]+f[j][k];
    //用这个新的更新所有前面的 
	return;
}
int main(){
	cin>>n>>m;
	for(int i=0;i<n;i++)
	cin>>a[i];
	for(int i=0;i<n;i++)
	for(int j=0;j<n;j++)
    {
		f[i][j]=1e9;
        //初始化为保证它不爆炸范围内的最大值 
	}
	for(int i=0;i<n;i++)
	f[i][i]=0;
	int s1,s2,s3;
	for(int i=1;i<=m;i++)
    {
		cin>>s1>>s2>>s3;
		f[s1][s2]=f[s2][s1]=s3;
        //初始化边长 
	}
	int q;
	cin>>q;
	int now=0;
	for(int i=1;i<=q;i++)
    {
        //处理各询问 
		cin>>s1>>s2>>s3;
		while(a[now]<=s3&&now<n)
        {
			updata(now);
            //依次更新点，使它可以被用来更新其他的点 
			now++;
		}
		if(a[s1]>s3||a[s2]>s3)
            cout<<-1<<'\n';
		else 
        {
			if(f[s1][s2]==1e9)
                cout<<-1<<'\n';
			else 
                cout<<f[s1][s2]<<'\n';
		}
	}

}

[NOIP2002 普及组] 产生数

题目描述

给出一个整数 \(n\) 和 \(k\) 个变换规则。

规则： - 一位数可变换成另一个一位数。 - 规则的右部不能为零。

例如：\(n=234,k=2\)。有以下两个规则：

• \(2\longrightarrow 5\)。
  
• \(3\longrightarrow 6\)。

上面的整数 \(234\) 经过变换后可能产生出的整数为（包括原数）:

• \(234\)。
• \(534\)。
• \(264\)。
• \(564\)。

共 \(4\) 种不同的产生数。

现在给出一个整数 \(n\) 和 \(k\) 个规则。求出经过任意次的变换（\(0\) 次或多次），能产生出多少个不同整数。

仅要求输出个数。

输入格式

第一行两个整数 \(n,k\)，含义如题面所示。

接下来 \(k\) 行，每行两个整数 \(x_i,y_i\)，表示每条规则。

输出格式

共一行，输出能生成的数字个数。

样例 #1

样例输入 #1

234 2
2 5
3 6

样例输出 #1

4

提示

对于 \(100\%\) 数据，满足 \(n \lt 10^{30}\)，\(k \le 15\)。

【题目来源】

NOIP 2002 普及组第三题

#include<bits/stdc++.h>
using namespace std;
string str;
int k;
const int N=101;
int v[N][N];
int f[N];
int num[N];
void floyd()
{
    for(int  k=0;k<=9;k++)
    {
        for(int i=0;i<=9;i++)
        {
            for(int j=0;j<=9;j++)
            {
             v[i][j]=(v[i][j]||(v[i][k]&&v[k][j]));   
            }
        }
    }
}
//floyd算法
//算出能不能i到j
int main()
{
cin>>str;
cin>>k;
    //输入
while(k--)
{
    int a,b;
    cin>>a>>b;
    v[a][b]=1;
}
    //可以转换
for(int i=0;i<=9;i++)
{
v[i][i]=1;
}
floyd();
for(int i=0;i<=9;i++)
{
for(int j=0;j<=9;j++)
{
  if(v[i][j])
  {
    f[i]++;
    //i可以变成多少种数字
  }  
}
}
int len = 2;
num[1] = 1;
for (int i = 0; i < (int)str.length(); i++)
{ 
    for (int j = 1; j <= 100; j++)
        num[j] *= f[str[i] - '0'];
    for (int j = 1; j <= 100; j++)
        if (num[j] >= 10)
        { // 进位
            num[j + 1] += num[j] / 10;
            num[j] %= 10;
        }
    while (num[len])
        len++; // 求出长度
}
for (int i = len - 1; i >= 1; i--)
    cout << num[i]; // 输出
return 0;
}

[USACO08JAN] Cow Contest S

题目描述

$ N (1 ≤ N ≤ 100) $ cows, conveniently numbered $ 1 ~ N $ , are participating in a programming contest. As we all know, some cows code better than others. Each cow has a certain constant skill rating that is unique among the competitors.

The contest is conducted in several head-to-head rounds, each between two cows. If cow $ A $ has a greater skill level than cow $ B (1 ≤ A ≤ N; 1 ≤ B ≤ N; A ≠ B) $, then cow $ A $ will always beat cow $ B $ .

Farmer John is trying to rank the cows by skill level. Given a list the results of $ M (1 ≤ M ≤ 4,500) $ two-cow rounds, determine the number of cows whose ranks can be precisely determined from the results. It is guaranteed that the results of the rounds will not be contradictory.

FJ的 \(N\)（\(1 \leq N \leq 100\)）头奶牛们最近参加了场程序设计竞赛。在赛场上，奶牛们按 \(1, 2, \cdots, N\) 依次编号。每头奶牛的编程能力不尽相同，并且没有哪两头奶牛的水平不相上下，也就是说，奶牛们的编程能力有明确的排名。 整个比赛被分成了若干轮，每一轮是两头指定编号的奶牛的对决。如果编号为 \(A\) 的奶牛的编程能力强于编号为 \(B\) 的奶牛 （\(1 \leq A, B \leq N\)，\(A \neq B\))，那么她们的对决中，编号为 \(A\) 的奶牛总是能胜出。 FJ 想知道奶牛们编程能力的具体排名，于是他找来了奶牛们所有 \(M\)（\(1 \leq M \leq 4,500\)）轮比赛的结果，希望你能根据这些信息，推断出尽可能多的奶牛的编程能力排名。比赛结果保证不会自相矛盾。

输入格式

第一行两个用空格隔开的整数 \(N, M\)。

第 \(2\sim M + 1\) 行，每行为两个用空格隔开的整数 \(A, B\) ，描述了参加某一轮比赛的奶牛的编号，以及结果（每行的第一个数的奶牛为胜者）。

输出格式

输出一行一个整数，表示排名可以确定的奶牛的数目。

样例 #1

样例输入 #1

5 5
4 3
4 2
3 2
1 2
2 5

样例输出 #1

2

提示

样例解释：

编号为 \(2\) 的奶牛输给了编号为 \(1, 3, 4\) 的奶牛，也就是说她的水平比这 \(3\) 头奶牛都差。而编号为 \(5\) 的奶牛又输在了她的手下，也就是说，她的水平比编号为 \(5\) 的奶牛强一些。于是，编号为 \(2\) 的奶牛的排名必然为第 \(4\)，编号为 \(5\) 的奶牛的水平必然最差。其他 \(3\) 头奶牛的排名仍无法确定。

f[i] [j]=f[i] [j]|(f[i] [k]&f[k] [j])表示i能否走到j，即要么一开始i能到j,要么i能到k，k再能到j。

那么这里表示的是i能否赢j。

#include<bits/stdc++.h>
using namespace std;
int a,b,n,m;
int f[101][101];
int ans;
int main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		cin>>a>>b;
		f[a][b]=1;
	}
for(int k=1;k<=n;k++)
{
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			f[i][j]=f[i][j]|f[i][k]&f[k][j];
			//表示是否连通
		}
	}
}	
	for(int i=1;i<=n;i++)
	{
		int gg=1;
		for(int j=1;j<=n;j++)
		{
			if(i==j)
			continue;
			else{
				gg=gg&(f[i][j]|f[j][i]);
                //最后是1肯定能够确定
			}
		}
	ans+=gg;	
	}
	cout<<ans;
}

[NOI2007] 社交网络

题目描述

在社交网络 ( Social Network ) 的研究中，我们常常使用图论概念去解释一些社会现象。不妨看这样的一个问题:
在一个社交圈子里有 \(n\) 个人，人与人之间有不同程度的关系。我们将这个关系网络对应到一个 \(n\) 个结点的无向图上，两个不同的人若互相认识，则在他们对应的结点之间连接一条无向边，并附上一个正数权值 \(c\) ，\(c\) 越小，表示两个人之间的关系越密切。我们可以用对应结点之间的最短路长度来衡量两个人 \(s\) 和 \(t\) 之间的关系密切程度，注意到最短路径上的其他结点为 \(s\) 和 \(t\) 的联系提供了某种便利，即这些结点对于 \(s\) 和 \(t\) 之间的联系有一定的重要程度。我们可以通过统计经过一个结点 \(v\) 的最短路径的数目来衡量该结点在社交网络中的重要程度。考虑到两个结点 \(A\) 和 \(B\) 之间可能会有多条最短路径。我们修改重要程度的定义如下：令 \(C_{s,t}\) 表示从s到t的不同的最短路的数目，\(C_{s,t}(v)\) 表示经过 \(v\) 从 \(s\) 到 \(t\) 的最短路的数目；则定义：

\[ I(v)=\sum_{s \ne v,t\ne v} \frac{C_{s,t}(v)}{C_{s,t}}\]

为结点 \(v\) 在社交网络中的重要程度。为了使 \(I(v)\) 和 \(C_{s,t}(v)\) 有意义，我们规定需要处理的社交网络都是连通的无向图，即任意两个结点之间都有一条有限长度的最短路径。现在给出这样一幅描述社交网络的加权无向图，请你求出每一个结点的重要程度。

输入格式

输入第一行有两个整数 \(n\) 和 \(m\) ，表示社交网络中结点和无向边的数目。
在无向图中，我们将所有结点从 \(1\) 到 \(n\) 进行编号。

接下来 \(m\) 行，每行用三个整数 \(a , b , c\) 描述一条连接结点 \(a\) 和 \(b\) ，权值为 \(c\) 的无向边。 注意任意两个结点之间最多有一条无向边相连，无向图中也不会出现自环（即不存在一条无向边的两个端点是相同的结点）。

输出格式

输出包括 \(n\) 行，每行一个实数，精确到小数点后 \(3\) 位。第 \(i\) 行的实数表示结点 \(i\) 在社交网络中的重要程度。

样例 #1

样例输入 #1

4 4
1 2 1
2 3 1
3 4 1
4 1 1

样例输出 #1

1.000
1.000
1.000
1.000

提示

对于1号结点而言，只有2号到4号结点和4号到2号结点的最短路经过1号结点，而2号结点和4号结点之间的最短路又有2条。因而根据定义，1号结点的重要程度计算为1/2+1/2=1。由于图的对称性，其他三个结点的重要程度也都是1。

对于 \(50\%\) 的数据， \(n \le 10 , m \le 45\)。
对于 \(100\%\) 的数据， \(n \le 100 , m \le 4500\) ，任意一条边的权值 \(c\) 是正整数且 \(1 \leqslant c \leqslant 1000\) 。
所有数据中保证给出的无向图连通，且任意两个结点之间的最短路径数目不超过 \(10^{10}\)。

可掌握点：floyd算法求路径数，和经过该点路径的条数

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=150;
ll dis[N][N];
ll fangan[N][N];
int n,m;
double ans[N];
ll INF;
void floyd()
{
    for (int k = 1; k <= n; k++)
    {
        for (int i = 1; i <= n; i++)
            {
                for (int j = 1; j <= n; j++)
                {
                    if(dis[i][k]==INF&&dis[k][j]==INF)
                    {
                        continue;
                    }
                    //都还未更新直接跳过
                    if (dis[i][j]>dis[i][k]+dis[k][j])
                    {
                        dis[i][j]=dis[i][k]+dis[k][j];
                        fangan[i][j]=fangan[i][k]*fangan[k][j];
                        continue;
                    }
                    //更新距离喝=和方案，注意是等于
                    else if(dis[i][j]==dis[i][k]+dis[k][j])
                    {
                        fangan[i][j]+=fangan[i][k]*fangan[k][j];
                    }
                    //更新方案，注意是+=
                }
            }
}
}
int main()
{
memset(dis, 0x7f, sizeof(dis));
    //初始化为最大值，因为求最短路
INF=dis[1][1];
    //记录一下方便统计
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
    ll x, y, z;
    cin >> x >> y >> z;
    dis[x][y] = dis[y][x] = z;
    fangan[x][y] = fangan[y][x] = 1;
}
    //输入距离和方案
floyd();
for(int i=1;i<=n;i++)
{
    for(int  j=1;j<=n;j++)
    for(int k=1;k<=n;k++)
    {
        if(i==j||j==k||i==k)
        {
            continue;
            //跳出
        }
if(dis[j][k]==dis[j][i]+dis[i][k])
{
    ans[i]+=(1.0 * fangan[j][i] * fangan[i][k]) / fangan[j][k];
}
//求答案，就是可以用这个点更新出来，证明经过了，就这样
    }
}

for(int i=1;i<=n;i++)
{
    printf("%0.3f\n", ans[i]);
    //格式化输出
}
}