背景

树状数组（Binary Index Tree, BIT）,最简单的树状数组支持两种操作，时间复杂度均为 O(log n)

  • 单点修改：更改数组中一个元素的值
  • 区间查询：查询一个区间内所有元素的和

其实以下这几种都可以解决：

1.单点修改，单点查询，2.区间修改，单点查询，3.区间查询，区间修改

介绍为：线段树能解决的问题，树状数组大部分也可以

因此优缺点很明显了：

正面：修改和查询操作复杂度于线段树一样都是logN,但是常数比线段树小，并且实现比线段树简单

负面：扩展性弱，线段树能解决的问题，树状数组不一定能解决.

我们要实现两种操作：单点修改和区间求和。对于普通数组而言，单点修改的时间复杂度是 O(1) ，但区间求和的时间复杂度是 O(n) 。

我们也可以用前缀和的方法维护这个数组，这样的话区间求和的时间复杂度就降到了O(1)，但是单点修改会影响后面所有的元素，时间复杂度是O(n)。

我们试图寻找一种结构，一方面，单点修改时需要更新的区间不会太多；另一方面，区间查询时需要用来组合的区间也不会太多。

现在进入学习阶段：

前置知识

lowbit 运算

lowbit ( n ) 定义为非负整数 n 在二进制表示下 “ 最低位的 1 及其后面的所有的 0 ” 的二进制构成的数值。

比如当 n = 5 的时候，5 的二进制是 ：0101 ， 所以有：lowbit ( 5 ) = 1

比如当 n = 10 的时候，10 的二进制是 ：1010，所以有： lowbit ( 10 ) = 2

代码为

1
2
3
4
int lowbit(int x){
	return x & -x ;
}
//取反再加1就是-x了，可以举个例子小小的自己证明一下

还有一种代码实现方法

1
2
3
4
int lowbit(int x) 
{	
    return x - (x & (x - 1));
}

原理

1
2
3
4
5
6
7
8
9
10
11
//我们设c[x]保存以x为根的子树种叶子节点值的和

//比如就是说

//c[4]=c[2]+c[3]+a[4]=c[1]+a[2]+a[3]+a[4]=a[1]+a[2]+a[3]+a[4]
//这个是可以看出来的罢
//接下来观察，4的二进制数字是0100
//2是0010
//1是0001
//可以发现根是叶子节点+lowbit(叶子节点)得到的
//如：c[4]=c[2+lowbit(2)]

因此我们可以推理得到单点修改的时候只需要一路往父节点修改就行了

1
2
3
4
5
int add(int x,int k)
{
	for(int i=x;i<=n;i+=lowbit(i))
	c[i]+=k;
}
1
2
//区间查询则是一个不断减去lowbit当前节点的过程，如：sum[7]=c[7]+c[6]+c[4];
//其中,6=7-lowbit(7),4=6-lowbit(6)，所以我们可以通过不断的-lowbit操作来实现求和
1
2
3
4
5
6
7
8
int ask(x){
	int sum = 0;
	for(int i=x;i;i-=lowbit(i)){
		sum+=t[i];
	}
	return sum;
}
//这就是1-x的和了

接下来可以借由前缀和的思想，求出[l,r]的和

1
2
3
4
5
6
7
8
9
int search(int L,int R)
{
	int ans = 0;
	for(int i=L-1;i;i-=lowbit(i))
	ans-=c[i];
	for(int i=R;i;i-=lowbit(i))
	ans+=c[i];
	return 0;
}

总代码如下：

【模板】树状数组 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

  • 将某一个数加上 \(x\)

  • 求出某区间每一个数的和

输入格式

第一行包含两个正整数 \(n,m\)，分别表示该数列数字的个数和操作的总个数。

第二行包含 \(n\) 个用空格分隔的整数，其中第 \(i\) 个数字表示数列第 \(i\) 项的初始值。

接下来 \(m\) 行每行包含 \(3\) 个整数，表示一个操作，具体如下：

  • 1 x k 含义：将第 \(x\) 个数加上 \(k\)

  • 2 x y 含义：输出区间 \([x,y]\) 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 \(2\) 的结果。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

样例输出 #1

1
2
14
16

提示

【数据范围】

对于 \(30\%\) 的数据，\(1 \le n \le 8\)，\(1\le m \le 10\)；
对于 \(70\%\) 的数据，\(1\le n,m \le 10^4\)；
对于 \(100\%\) 的数据，\(1\le n,m \le 5\times 10^5\)。

数据保证对于任意时刻，\(a\) 的任意子区间（包括长度为 \(1\) 和 \(n\) 的子区间）和均在 \([-2^{31}, 2^{31})\) 范围内。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
//直接作差版本，姑且这么说吧
#include<iostream>
using ll=long long; 
using namespace std;
int c[30000000];
int n,m;
int ans;
int lowbit(int x)
{
	return x&-x;
}
void add(int x,int k)
{
	for(int i=x;i<=n;i+=lowbit(i))
	c[i]+=k;
}
void search(int L,int R)
{
	for(int i=L-1;i;i-=lowbit(i))	
	ans-=c[i];	
	for(int i=R;i;i-=lowbit(i))
	ans+=c[i];
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		int number;
		cin>>number;
		add(i,number);
	}
	for(int i=1;i<=m;i++)
	{
		int choice,x,y;
		cin>>choice>>x>>y;
		if(choice==1)
        {
             add(x,y);
        }
		else
		{
			ans=0;
			search(x,y);
			cout<<ans<<'\n';
		}
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
//间接作差型
#include<bits/stdc++.h>
using namespace std;
int tree[30000000];
int n,m;
int lowbit(int x)
{
	return x&-x;
}
void add(int x,int y )
{
	for(int i=x;i<=n;i+=lowbit(i))
	{
		tree[i]+=y;
	}
}
int sum(int x)
{
	if(x==0)
	{
		return 0;
	}
	int ans=0;
	for(int i=x;i>0;i-=lowbit(i))
	{
		ans+=tree[i];
	}	
	return ans;
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		int a;
		cin>>a;
		add(i,a);
	}
	for(int i=1;i<=m;i++)
	{
		int x,y,z;
		cin>>x>>y>>z;
		if(x==1)
		{
			add(y,z);
		}
		if(x==2)
		{
			int end=sum(z)-sum(y-1);
			cout<<'\n';
		}
	}
	return 0;
}

进阶

【模板】树状数组 2

题目描述

如题，已知一个数列，你需要进行下面两种操作：

  1. 将某区间每一个数加上 \(x\)；

  2. 求出某一个数的值。

输入格式

第一行包含两个整数 \(N\)、\(M\)，分别表示该数列数字的个数和操作的总个数。

第二行包含 \(N\) 个用空格分隔的整数，其中第 \(i\) 个数字表示数列第 $i $ 项的初始值。

接下来 \(M\) 行每行包含 \(2\) 或 \(4\)个整数，表示一个操作，具体如下：

操作 \(1\)： 格式：1 x y k 含义：将区间 \([x,y]\) 内每个数加上 \(k\)；

操作 \(2\)： 格式：2 x 含义：输出第 \(x\) 个数的值。

输出格式

输出包含若干行整数，即为所有操作 \(2\) 的结果。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

样例输出 #1

1
2
6
10

提示

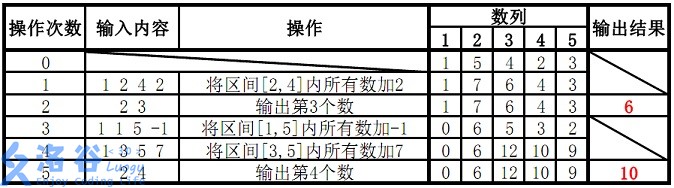
样例 1 解释：

故输出结果为 6、10。

数据规模与约定

对于 \(30\%\) 的数据：\(N\le8\)，\(M\le10\)；

对于 \(70\%\) 的数据：\(N\le 10000\)，\(M\le10000\)；

对于 \(100\%\) 的数据：\(1 \leq N, M\le 500000\)，\(1 \leq x, y \leq n\)，保证任意时刻序列中任意元素的绝对值都不大于 \(2^{30}\)。

有了单点修改，区间查询，自然有与之相对应的区间修改，单点查询。

不过这个时候就可以用差分数组了。

我们构造出原数组的差分数组，用刚刚我们的问题1的树状数组去维护就很妙了

对于区间修改的话，我们只需要对差分数组进行操作即可，例如对区间[L,R]+k,那么我们只需要更新差分数组add(L,k),add(R+1,-k)，这是差分数组的性质.

1
2
3
4
5
6
7
void add(int pos,int k)
{
	for(int i=pos;i<=n;i+=lowbit(i))
	c[i]+=k;
}
add(L,k);
add(R+1,-k);

单点查询就直接采用前缀和，直接回到第一问的区间查询

1
2
3
4
5
6
ll ask(int pos)//返回区间pos到1的总和
{
	ll ans=0;
	for(int i=pos;i;i-=lowbit(i)) ans+=c[i];
	return ans;
} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
//这个就没什么间接直接了，这样就好了
#include<iostream>
using namespace std;
int n,m;
int tree[10000000];
int lowbit(int x)
{
	return x&-x;
}
void add(int x,int y)
{
	for(int i=x;i<=n;i+=lowbit(i))
	{
		tree[i]+=y;
	}	
}
int sum(int x)
{
	int ans=0;
	for(int i=x;i>0;i-=lowbit(i))
	{
		ans+=tree[i];
	}
	return ans;	
}
int a[10000000];
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
	
		cin>>a[i];
		add(i,a[i]-a[i-1]);
        //差分操作
	}
	while(m--)
	{
		int opt;
		cin>>opt;
		if(opt==1)
		{
			int x,y,k;
			cin>>x>>y>>k;
		add(x,k);
		add(y+1,-k);
		}
		else
		{
			int x;
			cin>>x;
		cout<<sum(x)<<'\n';
		}	
	}
}

世间温柔，不过是芳春柳摇染花香，槐序蝉鸣入深巷，白茂叶落醉故乡。