模拟与高精

这是碰到不敢碰的题单（不过还是来碰一碰）

世间温柔，不过是芳春柳摇染花香，槐序蝉鸣入深巷，白茂叶落醉故乡。

祝大家新年顺利

[NOIP2003 普及组] 乒乓球

题目背景

国际乒联现在主席沙拉拉自从上任以来就立志于推行一系列改革，以推动乒乓球运动在全球的普及。其中 \(11\) 分制改革引起了很大的争议，有一部分球员因为无法适应新规则只能选择退役。华华就是其中一位，他退役之后走上了乒乓球研究工作，意图弄明白 \(11\) 分制和 \(21\) 分制对选手的不同影响。在开展他的研究之前，他首先需要对他多年比赛的统计数据进行一些分析，所以需要你的帮忙。

题目描述

华华通过以下方式进行分析，首先将比赛每个球的胜负列成一张表，然后分别计算在 \(11\) 分制和 \(21\) 分制下，双方的比赛结果（截至记录末尾）。

比如现在有这么一份记录，（其中 \(\texttt W\) 表示华华获得一分，\(\texttt L\) 表示华华对手获得一分）：

\(\texttt{WWWWWWWWWWWWWWWWWWWWWWLW}\)

在 \(11\) 分制下，此时比赛的结果是华华第一局 \(11\) 比 \(0\) 获胜，第二局 \(11\) 比 \(0\) 获胜，正在进行第三局，当前比分 \(1\) 比 \(1\)。而在 \(21\) 分制下，此时比赛结果是华华第一局 \(21\) 比 \(0\) 获胜，正在进行第二局，比分 \(2\) 比 \(1\)。如果一局比赛刚开始，则此时比分为 \(0\) 比 \(0\)。直到分差大于或者等于 \(2\)，才一局结束。

你的程序就是要对于一系列比赛信息的输入（\(\texttt{WL}\) 形式），输出正确的结果。

输入格式

每个输入文件包含若干行字符串，字符串有大写的 \(\texttt W\) 、 \(\texttt L\) 和 \(\texttt E\) 组成。其中 \(\texttt E\) 表示比赛信息结束，程序应该忽略 \(\texttt E\) 之后的所有内容。

输出格式

输出由两部分组成，每部分有若干行，每一行对应一局比赛的比分（按比赛信息输入顺序）。其中第一部分是 \(11\) 分制下的结果，第二部分是 \(21\) 分制下的结果，两部分之间由一个空行分隔。

样例 #1

样例输入 #1

WWWWWWWWWWWWWWWWWWWW
WWLWE

样例输出 #1

11:0
11:0
1:1

21:0
2:1

提示

每行至多 \(25\) 个字母，最多有 \(2500\) 行。

（注：事实上有一个测试点有 \(2501\) 行数据。）

【题目来源】

NOIP 2003 普及组第一题

#include<iostream>
#include<algorithm>
#include<string>
#include<math.h>
using namespace std;
int f[2] = { 11,21 };
int a[2500 * 25 + 100];
int n = 0;
int main()
{
	char c='0';
	while (c!='E')
	{
		cin >> c;
		if (c=='W')
		{
			a[n++] = 1;
		}
		else
		{
			a[n++] = 0;
		}

	}
    //输入统计
	for (int i = 0; i < 2; i++)
	{
		int w = 0;
		int l = 0;
		for (int j = 0; j < n; j++)
		{

if(a[j]==1)
{
w++;
}
            else
            {
l++;
            }
			if (max(w, l) >= f[i] && abs(w - l) >= 2)
			{
				cout << w << ":" << l << "\n";
				w = 0;
				l = 0;
			}
		}
		cout << w << ":" << l-1 << "\n";
		cout << "\n";
	}
	return 0;
}

[NOIP2015 普及组] 扫雷游戏

题目背景

NOIP2015 普及组 T2

题目描述

扫雷游戏是一款十分经典的单机小游戏。在 \(n\) 行 \(m\) 列的雷区中有一些格子含有地雷（称之为地雷格），其他格子不含地雷（称之为非地雷格）。玩家翻开一个非地雷格时，该格将会出现一个数字——提示周围格子中有多少个是地雷格。游戏的目标是在不翻出任何地雷格的条件下，找出所有的非地雷格。

现在给出 \(n\) 行 \(m\) 列的雷区中的地雷分布，要求计算出每个非地雷格周围的地雷格数。

注：一个格子的周围格子包括其上、下、左、右、左上、右上、左下、右下八个方向上与之直接相邻的格子。

输入格式

第一行是用一个空格隔开的两个整数 \(n\) 和 \(m\)，分别表示雷区的行数和列数。

接下来 \(n\) 行，每行 \(m\) 个字符，描述了雷区中的地雷分布情况。字符 \(\texttt{*}\) 表示相应格子是地雷格，字符 \(\texttt{?}\) 表示相应格子是非地雷格。相邻字符之间无分隔符。

输出格式

输出文件包含 \(n\) 行，每行 \(m\) 个字符，描述整个雷区。用 \(\texttt{*}\) 表示地雷格，用周围的地雷个数表示非地雷格。相邻字符之间无分隔符。

样例 #1

样例输入 #1

3 3
*??
???
?*?

样例输出 #1

*10
221
1*1

样例 #2

样例输入 #2

2 3
?*?
*??

样例输出 #2

2*1
*21

提示

对于 \(100\%\)的数据，\(1≤n≤100, 1≤m≤100\)。

#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
int dx[8] = {1,1,1,0,0,-1,-1,-1};
int dy [8] = {-1,0,1,-1,1,-1,0,1};
const  int N = 1000;
char a[N][N];

int main()
{
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			cin >> a[i][j];
		}
	}
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <=m ; j++)
		{
			if (a[i][j]=='*')
			{
				cout << a[i][j];	
			}
			else
			{
				int cnt = 0;
				for (int k =0 ; k <8; k++)
				{
					
					if (a[i+dx[k]][j+dy[k]]=='*')
					{
						cnt++;
					}
				}
				cout << cnt;
            }
		}
		cout << "\n";
	}
	return 0;
}

[NOIP2016 提高组] 玩具谜题

题目背景

NOIP2016 提高组 D1T1

题目描述

小南有一套可爱的玩具小人，它们各有不同的职业。

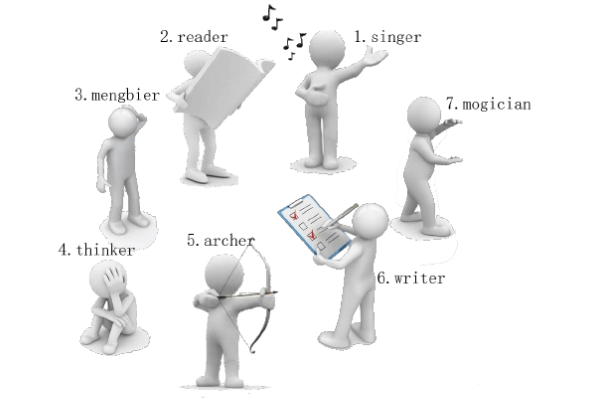
有一天，这些玩具小人把小南的眼镜藏了起来。小南发现玩具小人们围成了一个圈，它们有的面朝圈内，有的面朝圈外。如下图：

这时 singer 告诉小南一个谜题：“眼镜藏在我左数第 \(3\) 个玩具小人的右数第 \(1\) 个玩具小人的左数第 \(2\) 个玩具小人那里。”

小南发现，这个谜题中玩具小人的朝向非常关键，因为朝内和朝外的玩具小人的左右方向是相反的：面朝圈内的玩具小人，它的左边是顺时针方向，右边是逆时针方向；而面向圈外的玩具小人，它的左边是逆时针方向，右边是顺时针方向。

小南一边艰难地辨认着玩具小人，一边数着:

singer 朝内，左数第 \(3\) 个是 archer。

archer 朝外，右数第 \(1\) 个是 thinker。

thinker 朝外，左数第 \(2\) 个是 writer。

所以眼镜藏在 writer 这里！

虽然成功找回了眼镜，但小南并没有放心。如果下次有更多的玩具小人藏他的眼镜，或是谜题的长度更长，他可能就无法找到眼镜了。所以小南希望你写程序帮他解决类似的谜题。这样的谜題具体可以描述为：

有 \(n\) 个玩具小人围成一圈，已知它们的职业和朝向。现在第 \(1\) 个玩具小人告诉小南一个包含 \(m\) 条指令的谜題，其中第 \(z\) 条指令形如“向左数/右数第 \(s\) 个玩具小人”。你需要输出依次数完这些指令后，到达的玩具小人的职业。

输入格式

输入的第一行包含两个正整数 \(n,m\)，表示玩具小人的个数和指令的条数。

接下来 \(n\) 行，每行包含一个整数和一个字符串，以逆时针为顺序给出每个玩具小人的朝向和职业。其中 \(0\) 表示朝向圈内，\(1\) 表示朝向圈外。保证不会出现其他的数。字符串长度不超过 \(10\) 且仅由英文字母构成，字符串不为空，并且字符串两两不同。整数和字符串之间用一个空格隔开。

接下来 \(m\) 行，其中第 \(i\) 行包含两个整数 \(a_i,s_i\)，表示第 \(i\) 条指令。若 \(a_i=0\)，表示向左数 \(s_i\) 个人；若 \(a_i=1\)，表示向右数 \(s_i\) 个人。 保证 \(a_i\) 不会出现其他的数，\(1 \le s_i < n\)。

输出格式

输出一个字符串，表示从第一个读入的小人开始，依次数完 \(m\) 条指令后到达的小人的职业。

样例 #1

样例输入 #1

7 3
0 singer
0 reader
0 mengbier 
1 thinker
1 archer
0 writer
1 mogician 
0 3
1 1
0 2

样例输出 #1

writer

样例 #2

样例输入 #2

10 10
1 C
0 r
0 P
1 d
1 e
1 m
1 t
1 y
1 u
0 V
1 7
1 1
1 4
0 5
0 3
0 1
1 6
1 2
0 8
0 4

样例输出 #2

y

提示

样例 1 说明

这组数据就是【题目描述】中提到的例子。

子任务

子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解决一部分测试数据。

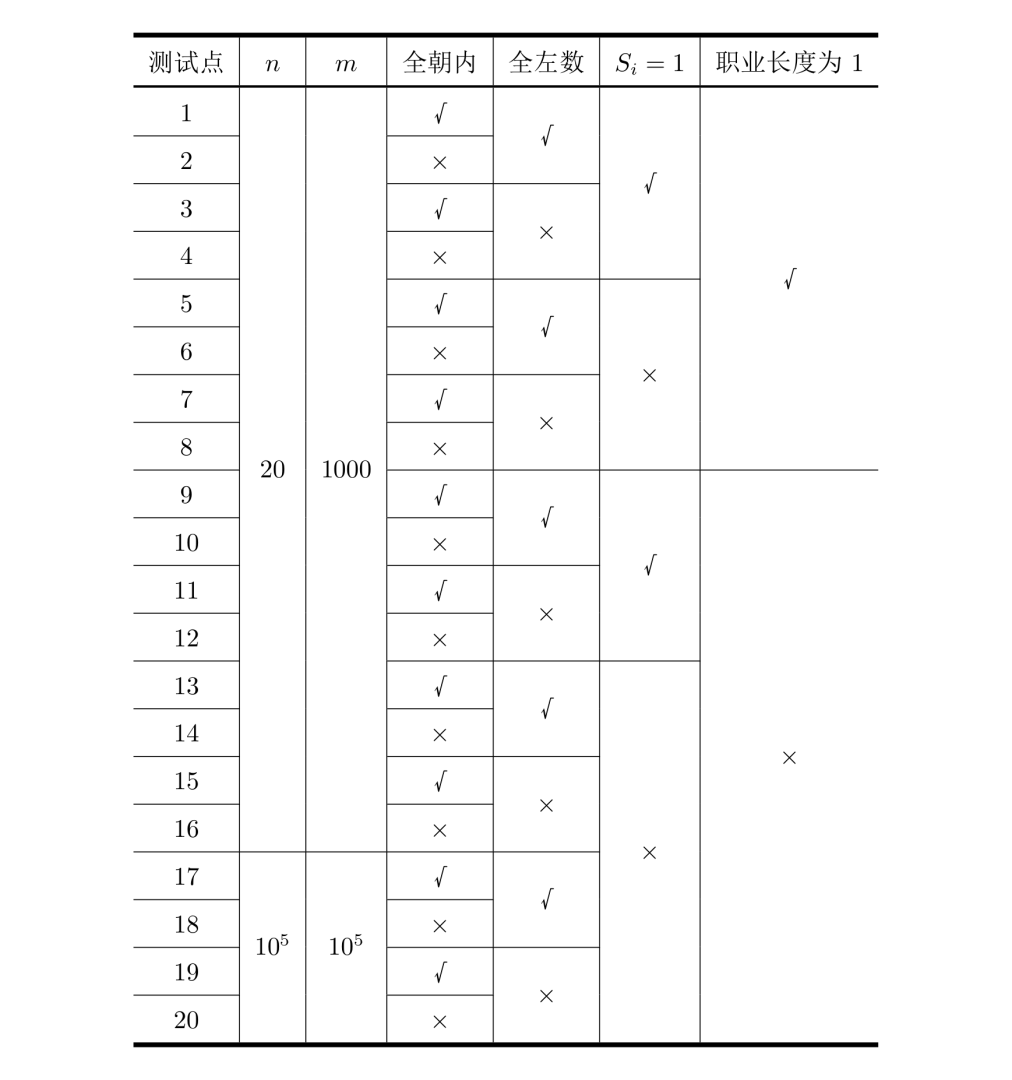
每个测试点的数据规模及特点如下表:

其中一些简写的列意义如下:

• 全朝内：若为 \(\surd\)，表示该测试点保证所有的玩具小人都朝向圈内；

• 全左数：若为 \(\surd\)，表示该测试点保证所有的指令都向左数，即对任意的 \(1\leq z\leq m, a_i=0\)；

• \(s=1\)：若为 \(\surd\)，表示该测试点保证所有的指令都只数 \(1\) 个，即对任意的 \(1\leq z\leq m,s_i=1\)；

职业长度为 \(1\)：若为 \(\surd\)，表示该测试点保证所有玩具小人的职业一定是一个长度为 \(1\) 的字符串。

#include<bits/stdc++.h>
using ll=unsigned long long;
using namespace std;
#define re register
#define rep(i,a,n) for(re int i=a;i<=n;i++)
#define rep(i,a,n) for(re int i=a;i>=n;i--)
#define r0 return 0;
#define inline in
struct node 
{
    int head;
    string name;
}a[100005];
int n,m,x,y; 
int main()
 {
    cin>>n>>m;
    for(int i=0;i<n;i++)
    {
        cin>>a[i].head>>a[i].name;
    }
    int now=0;
    for(int i=1;i<=m;i++)
    {
        cin>>x>>y;
        if(a[now].head==0&&x==0)now=(now+n-y)%n;
        else if(a[now].head==0&&x==1)now=(now+y)%n;
        else if(a[now].head==1&&x==0)now=(now+y)%n;
        else if(a[now].head==1&&x==1)now=(now+n-y)%n;
    }
    cout<<a[now].name;

}

A+B Problem（高精）

题目描述

高精度加法，相当于 a+b problem，不用考虑负数。

输入格式

分两行输入。\(a,b \leq 10^{500}\)。

输出格式

输出只有一行，代表 \(a+b\) 的值。

样例 #1

样例输入 #1

1
1

样例输出 #1

2

样例 #2

样例输入 #2

1001
9099

样例输出 #2

10100

提示

\(20\%\) 的测试数据，\(0\le a,b \le10^9\)；

\(40\%\) 的测试数据，\(0\le a,b \le10^{18}\)。

#include<iostream>

#include<algorithm>
#include<string>

using namespace std;
int c[100], d[100], e[100];
int main()
{
	string a;

	string b;

	cin >> a;

	cin >> b;


	int z = max(a.length(), b.length());

	for (int i = 1,j= a.length() -1; j>=0; i++,j--)
	{

		c[i] = a[j]-'0';

//逆序存储
	}

	for (int i = 1, j = b.length() - 1;  j >= 0; i++, j--)
	{

		d[i] = b[j]-'0';


	}

	for (int  i = 1; i <= z; i++)
	{
		e[i] += c[i] + d[i];

		e[i + 1] = e[i] / 10;

		e[i] = e[i] % 10;

	}
//高精过程
	if (e[z+1])
	{
		z+=1;
	}
//有进位要加一

	for (int i = z; i >= 1; i--)
	{

		cout << e[i];

	}
    //逆序输出
}

A*B Problem

题目描述

给出两个非负整数，求它们的乘积。

输入格式

输入共两行，每行一个非负整数。

输出格式

输出一个非负整数表示乘积。

样例 #1

样例输入 #1

1 
2

样例输出 #1

2

提示

每个非负整数不超过 \(10^{2000}\)。

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
char a1[10001],b1[10001];
int a[10001],b[10001],i,x,len,j,c[10001];
int main ()
{
    cin>>a1>>b1;//不解释，不懂看前面
    int lena=strlen(a1);//每个部分都很清楚
	int lenb=strlen(b1);//这只是方便你们复制
    for(i=1;i<=lena;i++)a[i]=a1[lena-i]-'0';
    for(i=1;i<=lenb;i++)b[i]=b1[lenb-i]-'0';
	for(i=1;i<=lenb;i++)
	for(j=1;j<=lena;j++)
	c[i+j-1]+=a[j]*b[i];
    for(i=1;i<lena+lenb;i++)
	if(c[i]>9)
	{
		c[i+1]+=c[i]/10;
		c[i]%=10;
	}
	len=lena+lenb;
    while(c[len]==0&&len>1)len--;
    for(i=len;i>=1;i--)cout<<c[i];
}

//乘法贡献在i+j-1这一位上
//然后进行操作

[NOIP1998 普及组] 阶乘之和

题目描述

用高精度计算出 \(S = 1! + 2! + 3! + \cdots + n!\)（\(n \le 50\)）。

其中 ! 表示阶乘，定义为 \(n!=n\times (n-1)\times (n-2)\times \cdots \times 1\)。例如，\(5! = 5 \times 4 \times 3 \times 2 \times 1=120\)。

输入格式

一个正整数 \(n\)。

输出格式

一个正整数 \(S\)，表示计算结果。

样例 #1

样例输入 #1

3

样例输出 #1

9

提示

【数据范围】

对于 \(100 \%\) 的数据，\(1 \le n \le 50\)。

【其他说明】

注，《深入浅出基础篇》中使用本题作为例题，但是其数据范围只有 \(n \le 20\)，使用书中的代码无法通过本题。

如果希望通过本题，请继续学习第八章高精度的知识。

NOIP1998 普及组 第二题

#include<iostream>
#include<algorithm>
#include<string>
#include<math.h>
#include<cmath>
using namespace std;
int a[1005];
int b[1005];
int main()
{
	int n;
	cin >> n;
	int i, j;
	a[0] = 1;
	b[0] = 1;
	for ( i = 2; i <=n ; i++)
	{
		for ( j = 0; j < 100; j++)
		{
			b[j] *= i;

		}
		for (j = 0; j < 100; j++)
		{
			if (b[j]>9)
			{
				b[j + 1] += b[j] / 10;
				b[j] = b[j] % 10;
			}
		}
		for (j = 0; j < 100; j++) {
			a[j] += b[j];
			if (a[j] > 9) {
				a[j + 1] += a[j] / 10;
				a[j] %= 10;
			}
		}


	}

	for (i = 100; i >= 0 && a[i] == 0; i--);
	for ( j = i; j >=0; j--)
	{
		cout << a[j];
	}
	return 0;
}

[1007] 魔法少女小Scarlet

题目描述

Scarlet 最近学会了一个数组魔法，她会在 \(n\times n\) 二维数组上将一个奇数阶方阵按照顺时针或者逆时针旋转 \(90^\circ\)。

首先，Scarlet 会把 \(1\) 到 \(n^2\) 的正整数按照从左往右，从上至下的顺序填入初始的二维数组中，然后她会施放一些简易的魔法。

Scarlet 既不会什么分块特技，也不会什么 Splay 套 Splay，她现在提供给你她的魔法执行顺序，想让你来告诉她魔法按次执行完毕后的二维数组。

输入格式

第一行两个整数 \(n,m\)，表示方阵大小和魔法施放次数。

接下来 \(m\) 行，每行 \(4\) 个整数 \(x,y,r,z\)，表示在这次魔法中，Scarlet 会把以第 \(x\) 行第 \(y\) 列为中心的 \(2r+1\) 阶矩阵按照某种时针方向旋转，其中 \(z=0\) 表示顺时针，\(z=1\) 表示逆时针。

输出格式

输出 \(n\) 行，每行 \(n\) 个用空格隔开的数，表示最终所得的矩阵

样例 #1

样例输入 #1

5 4
2 2 1 0
3 3 1 1
4 4 1 0
3 3 2 1

样例输出 #1

5 10 3 18 15
4 19 8 17 20
1 14 23 24 25
6 9 2 7 22
11 12 13 16 21

提示

对于50%的数据，满足 \(r=1\)

对于100%的数据 \(1\leq n,m\leq500\)，满足 \(1\leq x-r\leq x+r\leq n,1\leq y-r\leq y+r\leq n\)。

//翻转即是模拟，需要辅助数组
#include<bits/stdc++.h>
using namespace std;
int g[510][510],tot,f[510][510];
int main(){
	int n,m;
cin>>n>>m;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			g[i][j]=++tot;
	for(int i=1;i<=m;i++) {
		int a,b,r,opt;
	cin>>a>>b>>r>>opt;
		if(opt==0) {
			for(int i=a-r;i<=a+r;i++)
				for(int j=b-r;j<=b+r;j++)
					f[a-b+j][a+b-i] = g[i][j];
			for(int i=a-r;i<=a+r;i++)
				for(int j=b-r;j<=b+r;j++)
					g[i][j] = f[i][j];
		}
		else { 
			 for(int i=a-r;i<=a+r;i++)
				for(int j=b-r;j<=b+r;j++)
					f[a+b-j][b-a+i] = g[i][j];
			 for(int i=a-r;i<=a+r;i++)
				for(int j=b-r;j<=b+r;j++)
					g[i][j] = f[i][j];
		}
	}
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=n;j++)
		cout<<g[i][j]<<' ';
cout<<'\n';
	}
	return 0;
} 

[NOIP2014 提高组] 生活大爆炸版石头剪刀布

题目背景

NOIP2014 提高组 D1T1

题目描述

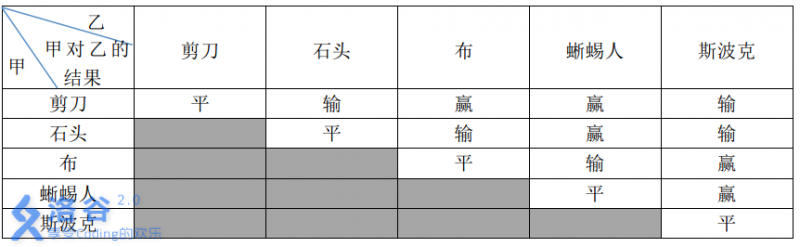
石头剪刀布是常见的猜拳游戏：石头胜剪刀，剪刀胜布，布胜石头。如果两个人出拳一样，则不分胜负。在《生活大爆炸》第二季第 8 集中出现了一种石头剪刀布的升级版游戏。

升级版游戏在传统的石头剪刀布游戏的基础上，增加了两个新手势：

斯波克:《星际迷航》主角之一。

蜥蜴人:《星际迷航》中的反面角色。

这五种手势的胜负关系如表一所示,表中列出的是甲对乙的游戏结果。

现在，小 A 和小 B 尝试玩这种升级版的猜拳游戏。已知他们的出拳都是有周期性规律的，但周期长度不一定相等。例如：如果小 A 以 石头-布-石头-剪刀-蜥蜴人-斯波克 长度为 \(6\) 的周期出拳,那么他的出拳序列就是 石头-布-石头-剪刀-蜥蜴人-斯波克-石头-布-石头-剪刀-蜥蜴人-斯波克-...，而如果小 B 以 剪刀-石头-布-斯波克-蜥蜴人 长度为 \(5\) 的周期出拳,那么他出拳的序列就是 剪刀-石头-布-斯波克-蜥蜴人-剪刀-石头-布-斯波克-蜥蜴人-...。

已知小 A 和小 B 一共进行 \(N\) 次猜拳。每一次赢的人得 \(1\) 分，输的得 \(0\) 分；平局两人都得 \(0\) 分。现请你统计 \(N\) 次猜拳结束之后两人的得分。

输入格式

第一行包含三个整数：\(N,N_A,N_B\)，分别表示共进行 \(N\) 次猜拳、小 A 出拳的周期长度，小 B 出拳的周期长度。数与数之间以一个空格分隔。

第二行包含 \(N_A\) 个整数,表示小 A 出拳的规律,第三行包含 \(N_B\) 个整数，表示小 B 出拳的规律。其中，\(0\) 表示 剪刀，\(1\) 表示 石头，\(2\) 表示 布，\(3\) 表示 蜥蜴人，\(4\) 表示 斯波克。数与数之间以一个空格分隔。

输出格式

输出一行，包含两个整数，以一个空格分隔，分别表示小 A、小 B 的得分。

样例 #1

样例输入 #1

10 5 6
0 1 2 3 4
0 3 4 2 1 0

样例输出 #1

6 2

样例 #2

样例输入 #2

9 5 5
0 1 2 3 4
1 0 3 2 4

样例输出 #2

4 4

提示

对于 \(100\%\) 的数据，\(0 < N \leq 200, 0 < N_A \leq 200, 0 < N_B \leq 200\) 。

#include<bits/stdc++.h>
using ll=unsigned long long;
using namespace std;
#define re register
#define rep(i,a,n) for(re int i=a;i<=n;i++)
#define rep(i,a,n) for(re int i=a;i>=n;i--)
#define r0 return 0;
#define inline in
const int MAXN = 200 + 10;
int n, na, nb, a[MAXN], b[MAXN], cnta, cntb;
int vs[5][5] = {{0,0,1,1,0},{1,0,0,1,0},{0,1,0,0,1},{0,0,1,0,1},{1,1,0,0,0}}; 
int main()
 {
 cin >> n >> na >> nb;
    for(int i = 0; i < na; i++) cin >> a[i];
    for(int i = 0; i < nb; i++) cin >> b[i];
    for(int i = 0; i < n; i++)
    {
        cnta += vs[a[i % na]][b[i % nb]]; 
        cntb += vs[b[i % nb]][a[i % na]];
    }
    cout << cnta << " " << cntb ;
	
	r0
}

[USACO2.4] 两只塔姆沃斯牛 The Tamworth Two

题目描述

两只牛逃跑到了森林里。Farmer John 开始用他的专家技术追捕这两头牛。你的任务是模拟他们的行为（牛和 John）。

追击在 \(10 \times 10\) 的平面网格内进行。一个格子可以是：一个障碍物，两头牛（它们总在一起），或者 Farmer John。两头牛和 Farmer John 可以在同一个格子内（当他们相遇时），但是他们都不能进入有障碍的格子。

一个格子可以是： - . 空地； - * 障碍物； - C 两头牛； - F Farmer John。

这里有一个地图的例子：

*...*.....
......*...
...*...*..
..........
...*.F....
*.....*...
...*......
..C......*
...*.*....
.*.*......

牛在地图里以固定的方式游荡。每分钟，它们可以向前移动或是转弯。如果前方无障碍（地图边沿也是障碍），它们会按照原来的方向前进一步。否则它们会用这一分钟顺时针转 90 度。 同时，它们不会离开地图。

Farmer John 深知牛的移动方法，他也这么移动。

每次（每分钟）Farmer John 和两头牛的移动是同时的。如果他们在移动的时候穿过对方，但是没有在同一格相遇，我们不认为他们相遇了。当他们在某分钟末在某格子相遇，那么追捕结束。

读入十行表示地图。每行都只包含 10 个字符，表示的含义和上面所说的相同。保证地图中只有一个 F 和一个 C。F 和 C 一开始不会处于同一个格子中。

计算 Farmer John 需要多少分钟来抓住他的牛，假设牛和 Farmer John 一开始的行动方向都是正北（即上）。 如果 John 和牛永远不会相遇，输出 0。

输入格式

输入共十行，每行 10 个字符，表示如上文描述的地图。

输出格式

输出一个数字，表示 John 需要多少时间才能抓住牛们。如果 John 无法抓住牛，则输出 0。

样例 #1

样例输入 #1

*...*.....
......*...
...*...*..
..........
...*.F....
*.....*...
...*......
..C......*
...*.*....
.*.*......

样例输出 #1

49

提示

翻译来自NOCOW

USACO 2.4

从题解那学到了顺时针数组存储

以及特征值判重

两个也许有用的地方

#include<bits/stdc++.h>
using namespace std;
bool zt[160005];
char mp[11][11];
int cx,cy,cf,fx,fy,ff,xx[4]={-1,0,1,0},yy[4]={0,1,0,-1},nt,stp;
int main()
{
    for(int i=0;i<10;i++)
    cin>>mp[i];
    for(int i=0;i<10;i++)
    for(int j=0;j<10;j++)
    {
        if(mp[i][j]=='F')//遇到农夫
        fx=i,fy=j;//设定初始坐标
        if(mp[i][j]=='C')//遇到牛
        cx=i,cy=j;//设定初始坐标
    }
    while(1)
    {
        if(fx==cx&&fy==cy)//相遇了
        {
       cout<<stp;
            return 0;//退出
        }
        nt=fx+fy*10+cx*100+cy*1000+ff*10000+cf*40000;//生成特征值
        if(zt[nt])//如果出现过了，则无解
        {
          cout<<0;
            return 0;
        }
        zt[nt]=1;//保存特征值
        if(fx+xx[ff]<0||fx+xx[ff]>=10||fy+yy[ff]<0||fy+yy[ff]>=10||mp[fx+xx[ff]][fy+yy[ff]]=='*')//判断农夫是否还能向前走
        ff=(ff+1)%4;//如果不行，转向
        else fx=fx+xx[ff],fy=fy+yy[ff];//否则继续向前
        if(cx+xx[cf]<0||cx+xx[cf]>=10||cy+yy[cf]<0||cy+yy[cf]>=10||mp[cx+xx[cf]][cy+yy[cf]]=='*')//判断牛是否还能向前走
        cf=(cf+1)%4;//如果不行，转向
        else cx=cx+xx[cf],cy=cy+yy[cf];//否则继续向前
        stp++;//增加步数
    }
    return 0;
}

[NOIP2007 提高组] 字符串的展开

题目描述

在初赛普及组的“阅读程序写结果”的问题中，我们曾给出一个字符串展开的例子：如果在输入的字符串中，含有类似于 d-h 或者 4-8 的字串，我们就把它当作一种简写，输出时，用连续递增的字母或数字串替代其中的减号，即，将上面两个子串分别输出为 defgh 和 45678。在本题中，我们通过增加一些参数的设置，使字符串的展开更为灵活。具体约定如下：

1. 遇到下面的情况需要做字符串的展开：在输入的字符串中，出现了减号 - ，减号两侧同为小写字母或同为数字，且按照 ASCII 码的顺序，减号右边的字符严格大于左边的字符。

2. 参数 \(p_1\)：展开方式。\(p_1=1\) 时，对于字母子串，填充小写字母；\(p_1=2\) 时，对于字母子串，填充大写字母。这两种情况下数字子串的填充方式相同。\(p_1=3\) 时，不论是字母子串还是数字字串，都用与要填充的字母个数相同的星号 * 来填充。

3. 参数 \(p_2\)：填充字符的重复个数。\(p_2=k\) 表示同一个字符要连续填充 \(k\) 个。例如，当 \(p_2=3\) 时，子串d-h 应扩展为 deeefffgggh。减号两边的字符不变。

4. 参数 \(p_3\)：是否改为逆序：\(p_3=1\) 表示维持原来顺序，\(p_3=2\) 表示采用逆序输出，注意这时候仍然不包括减号两端的字符。例如当 \(p_1=1\)、\(p_2=2\)、\(p_3=2\) 时，子串 d-h 应扩展为 dggffeeh。

5. 如果减号右边的字符恰好是左边字符的后继，只删除中间的减号，例如：d-e 应输出为 de，3-4 应输出为 34。如果减号右边的字符按照 ASCII 码的顺序小于或等于左边字符，输出时，要保留中间的减号，例如：d-d 应输出为 d-d，3-1 应输出为 3-1。

输入格式

共两行。

第 \(1\) 行为用空格隔开的 \(3\) 个正整数，依次表示参数 \(p_1,p_2,p_3\)。

第 \(2\) 行为一行字符串，仅由数字、小写字母和减号 - 组成。行首和行末均无空格。

输出格式

共一行，为展开后的字符串。

样例 #1

样例输入 #1

1 2 1
abcs-w1234-9s-4zz

样例输出 #1

abcsttuuvvw1234556677889s-4zz

样例 #2

样例输入 #2

2 3 2
a-d-d

样例输出 #2

aCCCBBBd-d

提示

\(40\%\) 的数据满足：字符串长度不超过 \(5\)。

\(100\%\) 的数据满足：\(1 \le p_1 \le 3,1 \le p_2 \le 8,1 \le p_3 \le 2\)。字符串长度不超过 \(100\)。

NOIP 2007 提高第二题

#include <bits/stdc++.h>
using namespace std;
using ll=long long;
#define r0 return 0;
int p1,p2,p3;
vector<char> ans;
string s;
int main()
{
    cin >> p1 >> p2 >> p3 >> s;
    for(int i=0;i<s.size();i++)
    {
        if(s[i]!='-') ans.push_back(s[i]);
        
        else if((i==0 || i==s.size()-1) && s[i]=='-' ) ans.push_back('-');
        
        else if(s[i]=='-' && (s[i-1]=='-' || s[i+1]=='-')) ans.push_back('-');
        
        else if(s[i]=='-')
        {
            if(s[i-1]>=s[i+1] || (s[i-1]<58 && s[i+1]>96)) ans.push_back('-');
            else if(s[i+1]==s[i-1]+1) continue;
            else
            {
                if(p1==3)
                {
                    for(int k=1;k<=(s[i+1]-s[i-1]-1)*p2;k++) ans.push_back('*');
                }
                //判断*
                else if(s[i+1]<=57 && s[i+1]>=48 && s[i-1]<=57 && s[i-1]>=48)
                {
                    if(p3==1)
                    {
                        for(int k=s[i-1]+1;k<=s[i+1]-1;k++)
                            for(int j=1;j<=p2;j++)
                                ans.push_back(char(k));
                    }
                    else if(p3==2)
                    {
                        for(int k=s[i+1]-1;k>=s[i-1]+1;k--)
                            for(int j=1;j<=p2;j++)
                                ans.push_back(char(k));                        
                    }
                }
                //判断数字
                //正序或逆序，此时可以不用看p1
                  
                else if(s[i+1]<=122 && s[i+1]>=97 && s[i-1]<=122 && s[i-1]>=97)
                {
                    if(p1==1)
                    {
                        if(p3==1)
                        {
                            for(int k=s[i-1]+1;k<=s[i+1]-1;k++)
                                for(int j=1;j<=p2;j++)
                                    ans.push_back(char(k));                            
                        }
                        else if(p3==2)
                        {
                            for(int k=s[i+1]-1;k>=s[i-1]+1;k--)
                                for(int j=1;j<=p2;j++)
                                    ans.push_back(char(k));                                
                        }
                    }
                    else if(p1==2)
                    {
                        if(p3==1)
                        {
                            for(int k=s[i-1]+1;k<=s[i+1]-1;k++)
                                for(int j=1;j<=p2;j++)
                                    ans.push_back(char(k-32));                                
                        }
                        else if(p3==2)
                        {
                            for(int k=s[i+1]-1;k>=s[i-1]+1;k--)
                                for(int j=1;j<=p2;j++)
                                    ans.push_back(char(k-32));                                
                        }
                    }
                    //判断字母，需要加入p1的判断
                }
            }
        }
    }
    for(int i=0;i<ans.size();i++) cout << ans[i];
r0
    
}

[NOIP2006 提高组] 作业调度方案

题目描述

我们现在要利用 \(m\) 台机器加工 \(n\) 个工件，每个工件都有 \(m\) 道工序，每道工序都在不同的指定的机器上完成。每个工件的每道工序都有指定的加工时间。

每个工件的每个工序称为一个操作，我们用记号 j-k 表示一个操作，其中 \(j\) 为 \(1\) 到 \(n\) 中的某个数字，为工件号；\(k\) 为 \(1\) 到 \(m\) 中的某个数字，为工序号，例如 2-4 表示第 \(2\) 个工件第 \(4\) 道工序的这个操作。在本题中，我们还给定对于各操作的一个安排顺序。

例如，当 \(n=3,m=2\) 时，1-1,1-2,2-1,3-1,3-2,2-2 就是一个给定的安排顺序，即先安排第 \(1\) 个工件的第 \(1\) 个工序，再安排第 \(1\) 个工件的第 \(2\) 个工序，然后再安排第 \(2\) 个工件的第 \(1\) 个工序，等等。

一方面，每个操作的安排都要满足以下的两个约束条件。

1. 对同一个工件，每道工序必须在它前面的工序完成后才能开始；

2. 同一时刻每一台机器至多只能加工一个工件。

另一方面，在安排后面的操作时，不能改动前面已安排的操作的工作状态。

由于同一工件都是按工序的顺序安排的，因此，只按原顺序给出工件号，仍可得到同样的安排顺序，于是，在输入数据中，我们将这个安排顺序简写为 1 1 2 3 3 2。

还要注意，“安排顺序”只要求按照给定的顺序安排每个操作。不一定是各机器上的实际操作顺序。在具体实施时，有可能排在后面的某个操作比前面的某个操作先完成。

例如，取 \(n=3,m=2\)，已知数据如下（机器号/加工时间）：

工件号	工序 1	工序 2
\(1\)	\(1/3\)	\(2/2\)
\(2\)	\(1/2\)	\(2/5\)
\(3\)	\(2/2\)	\(1/4\)

则对于安排顺序 1 1 2 3 3 2，下图中的两个实施方案都是正确的。但所需要的总时间分别是 \(10\) 与 \(12\)。

方案 1，用时 \(10\)：

时间	1	2	3	4	5	6	7	8	9	10
机器 1 执行工序	1-1	1-1	1-1	2-1	2-1	3-2	3-2	3-2	3-2	无
机器 2 执行工序	3-1	3-1	无	1-2	1-2	2-2	2-2	2-2	2-2	2-2

方案 2，用时 \(12\)：

时间	1	2	3	4	5	6	7	8	9	10	11	12
机器 1 执行工序	1-1	1-1	1-1	2-1	2-1	无	无	3-2	3-2	3-2	3-2	无
机器 2 执行工序	无	无	无	1-2	1-2	3-1	3-1	2-2	2-2	2-2	2-2	2-2

当一个操作插入到某台机器的某个空档时（机器上最后的尚未安排操作的部分也可以看作一个空档），可以靠前插入，也可以靠后或居中插入。为了使问题简单一些，我们约定：在保证约束条件 \((1.)(2.)\) 的条件下，尽量靠前插入。并且，我们还约定，如果有多个空档可以插入，就在保证约束条件 \((1.)(2.)\) 的条件下，插入到最前面的一个空档。于是，在这些约定下，上例中的方案一是正确的，而方案二是不正确的。

显然，在这些约定下，对于给定的安排顺序，符合该安排顺序的实施方案是唯一的，请你计算出该方案完成全部任务所需的总时间。

输入格式

第 \(1\) 行为两个正整数 \(m\), \(n\)，用一个空格隔开， 其中 \(m(<20)\) 表示机器数，\(n(<20)\) 表示工件数。

第 \(2\) 行：\(m \times n\) 个用空格隔开的数，为给定的安排顺序。

接下来的 \(2n\) 行，每行都是用空格隔开的 \(m\) 个正整数，每个数不超过 \(20\)。

其中前 \(n\) 行依次表示每个工件的每个工序所使用的机器号，第 \(1\) 个数为第 \(1\) 个工序的机器号，第 \(2\) 个数为第 \(2\) 个工序机器号，等等。

后 \(n\) 行依次表示每个工件的每个工序的加工时间。

可以保证，以上各数据都是正确的，不必检验。

输出格式

\(1\) 个正整数，为最少的加工时间。

样例 #1

样例输入 #1

2 3
1 1 2 3 3 2
1 2 
1 2 
2 1
3 2 
2 5 
2 4

样例输出 #1

10

提示

NOIP 2006 提高组 第三题

#include<bits/stdc++.h>
using namespace std;

int m, n;
int _list[501];
struct Information {
    int id;
    // 在第 id 台机器上加工
    int cost;
    // 花费 cost 时间
} a[21][21];
// a[第几个工件][第几步]
int mac[21][100001] = {0};
// mac[机器编号][时间（话说我也不知道时间最大是多少，反正在空间限制内尽量大）]
int step[21] = {0};
// 每个工件加工到了第几步
int las_time[21] = {0};
// 每个工件上次是 las_time[工件编号] 时加工完的
int ans = 0;
int main()
{
  cin>>m>>n;
    for (int i = 1; i <= m * n; i++) {
   cin>>_list[i];
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
         cin>>a[i][j].id;
        }
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
         cin>>a[i][j].cost;
        }
    }

    for (int i = 1; i <= m * n; i++) {
        int now = _list[i];
        step[now]++;
        int id = a[now][step[now]].id, cost = a[now][step[now]].cost;
     
        int s = 0;
        for (int j = las_time[now] + 1; ; j++) {
            if (mac[id][j] == 0) {
                s++;
            } else {
                s = 0;
            }
            if (s == cost) {
                for (int k = j - cost + 1; k <= j; k++) {
                    mac[id][k] = 1;
                }
                if (j > ans) ans = j;
                las_time[now] = j;
                break;
            }
        }
    }
cout<<ans;
}

帮贡排序

题目背景

在 absi2011 的帮派里，死号偏多。现在 absi2011 和帮主等人联合决定，要清除一些死号，加进一些新号，同时还要鼓励帮贡多的人，对帮派进行一番休整。

题目描述

目前帮派内共最多有一位帮主，两位副帮主，两位护法，四位长老，七位堂主，二十五名精英，帮众若干。

现在 absi2011 要对帮派内几乎所有人的职位全部调整一番。他发现这是个很难的事情。于是要求你帮他调整。

他给你每个人的以下数据：

他的名字（长度不会超过 \(30\)），他的原来职位，他的帮贡，他的等级。

他要给帮贡最多的护法的职位，其次长老，以此类推。

可是，乐斗的显示并不按帮贡排序而按职位和等级排序。

他要你求出最后乐斗显示的列表(在他调整过职位后)：职位第一关键字，等级第二关键字。

注意：absi2011 无权调整帮主、副帮主的职位，包括他自己的（这不是废话么..）

他按原来的顺序给你（所以，等级相同的，原来靠前的现在也要靠前，因为经验高低的原因，但此处为了简单点省去经验。）

输入格式

第一行一个正整数 \(n\)，表示星月家园内帮友的人数。

下面 \(n\) 行每行两个字符串两个整数，表示每个人的名字、职位、帮贡、等级。

输出格式

一共输出 \(n\) 行，每行包括排序后乐斗显示的名字、职位、等级。

样例 #1

样例输入 #1

9
DrangonflyKang BangZhu 100000 66
RenZaiJiangHu FuBangZhu 80000 60
absi2011 FuBangZhu 90000 60
BingQiLingDeYanLei HuFa 89000 58
Lcey HuFa 30000 49
BangYou3 ZhangLao 1000 1
BangYou1 TangZhu 100 40
BangYou2 JingYing 40000 10
BangYou4 BangZhong 400 1

样例输出 #1

DrangonflyKang BangZhu 66
RenZaiJiangHu FuBangZhu 60
absi2011 FuBangZhu 60
BingQiLingDeYanLei HuFa 58
BangYou2 HuFa 10
Lcey ZhangLao 49
BangYou1 ZhangLao 40
BangYou3 ZhangLao 1
BangYou4 ZhangLao 1

提示

各种职位用汉语拼音代替。

如果职位剩 \(1\) 个，而有 \(2\) 个帮贡相同的人，则选择原来在前的现在当选此职位。

另： 帮派名号：星月家园

帮主尊号：Dragonfly Kang

帮派ID：2685023

帮派等级：4

帮派人数：101/110

帮派技能：

星月家园资料，欢迎各位豆油加入^_

【数据范围】

对于 \(10\%\) 的数据，保证 \(n=3\)。

对于 \(40\%\) 的数据，保证各个人的帮贡均为 \(0\)。

对于 \(100\%\) 的数据，保证 \(3\leq n\leq 110\)，各个名字长度\(\leq30\)，\(0\leq\) 各个人的帮贡 \(\leq1000000000\)， \(1\leq\) 各个人等级 \(\leq 150\)。

保证职位必定为 \(\texttt{BangZhu}\)，\(\texttt{FuBangZhu}\)，\(\texttt{HuFa}\)，\(\texttt{ZhangLao}\)，\(\texttt{TangZhu}\)，\(\texttt{JingYing}\)，\(\texttt{BangZhong}\) 之中的一个

保证有一名帮主，保证有两名副帮主，保证有一名副帮主叫 absi2011

不保证一开始帮派里所有职位都是满人的，但排序后分配职务请先分配高级职位。例如原来设一名护法现在设两名。

保证名字不重复。

【题目来源】

fight.pet.qq.com

absi2011 授权题目

表面模拟，实则暗含结构体排序（感觉可以放排序题单）

#include<bits/stdc++.h>
using namespace std;
int n;
struct node{
	string na,zw,xzw;
	long long bg;
	int le,h;
}ab[115];
int change(string a){
	if (a=="BangZhu") return 0;
	if (a=="FuBangZhu") return 1;
	if (a=="HuFa") return 2;
	if (a=="ZhangLao") return 3;
	if (a=="TangZhu") return 4;
	if (a=="JingYing") return 5;
	if (a=="BangZhong") return 6;
}
int cmp1(node x,node y){
	if (x.bg==y.bg) return x.h<y.h;
	else return x.bg>y.bg;
}
//这里没有等级排序有点接受不了（），但似乎要这样才能过（）
int cmp2(node x,node y){
	if (change(x.xzw)==change(y.xzw)){
		if (x.le==y.le) return x.h<y.h;
		return x.le>y.le;
	}
	return change(x.xzw)<change(y.xzw);
}

int main(){
	cin>>n;
	for (int i=1;i<=n;i++){
		cin>>ab[i].na>>ab[i].zw>>ab[i].bg>>ab[i].le;
		ab[i].h=i;
	}
	sort(ab+4,ab+1+n,cmp1);
	for (int i=1;i<=n;i++){
		if (i==1) ab[i].xzw="BangZhu";
		else if (i==2||i==3) ab[i].xzw="FuBangZhu";
		else if (i==4||i==5) ab[i].xzw="HuFa";
		else if (i>=6&&i<=9) ab[i].xzw="ZhangLao";
		else if (i>=10&&i<=16) ab[i].xzw="TangZhu";
		else if (i>=17&&i<=41) ab[i].xzw="JingYing";
		else ab[i].xzw="BangZhong";
	}
	sort(ab+1,ab+1+n,cmp2);
	for (int i=1;i<=n;i++){
		cout<<ab[i].na<<" "<<ab[i].xzw<<" "<<ab[i].le<<'\n';
	}

}

阶乘数码

题目描述

求 \(n!\) 中某个数码出现的次数。

输入格式

第一行为 \(t(t \leq 10)\)，表示数据组数。接下来 \(t\) 行，每行一个正整数 \(n(n \leq 1000)\) 和数码 \(a\)。

输出格式

对于每组数据，输出一个整数，表示 \(n!\) 中 \(a\) 出现的次数。

样例 #1

样例输入 #1

2
5 2
7 0

样例输出 #1

1
2

#include<bits/stdc++.h>
using namespace std;
int a[5000];
int main()
{
    int t;
    cin>>t;
    while (t--)
    {
memset(a,0,sizeof a);
        a[1]=1;
        int n,i,j,k,m;
        int p=1,jw=0;
       cin>>n>>m;
        for(i=2;i<=n;i++)
        {
            jw=0;
            for(j=1;j<=p;j++)//高精度*单精度。
            {
                a[j]=a[j]*i+jw;//高精度*单精度+进位。
                jw=a[j]/10;//设置进位。
                a[j]=a[j]%10;
            }
            while(jw>0)
            {
                a[j]=jw%10;
                jw/=10;
                j++;
            }
            p=j-1;
        }
        long long sum=0;
        for (i=p;i>=1;i--)
        {
            if (a[i]==m)
            sum++;
        }
        cout<<sum<<'\n';
    }
 
}

最大乘积

题目描述

一个正整数一般可以分为几个互不相同的自然数的和，如 \(3=1+2\)，\(4=1+3\)，\(5＝1+4=2+3\)，\(6=1+5＝2+4\)。

现在你的任务是将指定的正整数 \(n\) 分解成若干个互不相同的自然数的和，且使这些自然数的乘积最大。

输入格式

只一个正整数 \(n\)，（\(3 \leq n \leq 10000\)）。

输出格式

第一行是分解方案，相邻的数之间用一个空格分开，并且按由小到大的顺序。

第二行是最大的乘积。

样例 #1

样例输入 #1

10

样例输出 #1

2 3 5
30

连续乘积最大

有两种情况

如果刚好连续差1，就最大加一，2扔掉

否则就把刚好差的数字扔掉

高精度写法

#include<iostream>
using namespace std;
int a[10001]={};
int s[10001]={};
int n,len=1;
void mul(int x)
{
	for(int i=1;i<=len;i++)s[i]*=x;
	//乘法
	for(int i=1;i<=len;i++)
	{
		s[i+1]+=s[i]/10;
		s[i]%=10;
	}
	while(s[len+1]>0)
	{
		len++;
		s[len+1]+=s[len]/10;
		s[len]%=10;
	}
}
int main()
{
	cin>>n;
	if(n==3)
	{
		cout<<1<<' '<<2<<'\n';
		cout<<2<<'\n';
		return 0;
	}
	if(n==4)
	{
		cout<<1<<' '<<3<<'\n';
		cout<<3<<'\n';
		return 0;
	}
	s[0]=s[1]=1;
	int Sum=0,tot=0;
	for(int i=2;Sum<n;Sum+=i,i++)a[++tot]=i;
	if(Sum>n+1)a[Sum-n-1]=0;
	else if(Sum==n+1)a[tot]++,a[1]=0;
	
	for(int i=1;i<=tot;i++)
	{
		if(a[i])
		{
			cout<<a[i]<<' ';
			mul(a[i]);
		}
	}
	cout<<'\n';
	for(int i=len;i>=1;i--)
		cout<<s[i];
}

[NOIP2003 普及组] 麦森数

题目描述

形如 \(2^{P}-1\) 的素数称为麦森数，这时 \(P\) 一定也是个素数。但反过来不一定，即如果 \(P\) 是个素数，\(2^{P}-1\) 不一定也是素数。到 1998 年底，人们已找到了 37 个麦森数。最大的一个是 \(P=3021377\)，它有 909526 位。麦森数有许多重要应用，它与完全数密切相关。

任务：输入 \(P(1000<P<3100000)\)，计算 \(2^{P}-1\) 的位数和最后 \(500\) 位数字（用十进制高精度数表示）

输入格式

文件中只包含一个整数 \(P(1000<P<3100000)\)

输出格式

第一行：十进制高精度数 \(2^{P}-1\) 的位数。

第 \(2\sim 11\) 行：十进制高精度数 \(2^{P}-1\) 的最后 \(500\) 位数字。（每行输出 \(50\) 位，共输出 \(10\) 行，不足 \(500\) 位时高位补 \(0\)）

不必验证 \(2^{P}-1\) 与 \(P\) 是否为素数。

样例 #1

样例输入 #1

1279

样例输出 #1

386
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000104079321946643990819252403273640855
38615262247266704805319112350403608059673360298012
23944173232418484242161395428100779138356624832346
49081399066056773207629241295093892203457731833496
61583550472959420547689811211693677147548478866962
50138443826029173234888531116082853841658502825560
46662248318909188018470682222031405210266984354887
32958028878050869736186900714720710555703168729087

提示

【题目来源】

NOIP 2003 普及组第四题

image-20240214165851996

#include<bits/stdc++.h>
using namespace std;

int P;
long long a[510];

long long POW2(int a)
{
    long long res=1;
    for(int i=1;i<=a;i++)
    {
        res*=2;
    }
    return res;
}
int main()
{
    cin>>P;
    cout<<ceil(P*log10(2))<<'\n'; 
    long long tmp=POW2(32);      
    a[500]=1;
    int t32=P/32;                 
	int t1=P-t32*32;            
    for(int T=1;T<=t32;T++)
    {
        for(int i=500;i>=1;i--)
        {
            a[i]*=tmp;            
        }
        for(int i=500;i>=1;i--)
        {
            a[i-1]+=a[i]/10;
            a[i]%=10;             
        }
    }
    for(int T=1;T<=t1;T++)
    {
        for(int i=500;i>=1;i--)
        {
            a[i]*=2;              
        }
        for(int i=500;i>=1;i--)
        {
            a[i-1]+=a[i]/10;
            a[i]%=10;             
        }
    }
    a[500]--;
    //直接减去即可
    for(int i=1;i<=500;i++)
    {
        cout<<a[i];
        if(i%50==0) cout<<'\n';
    }
    

}