模糊综合评价模型

核心在于模糊的概念

概述

数学归纳法

image-20240128192713567

数学的量的划分

确定性

不确定性

image-20240128192829255

模糊数学

image-20240128192918227

经典集合和模糊集合的基本概念

经典集合

image-20240128193114838

模糊集合：描述模糊性概念的集合

image-20240128193422098

表示方法

image-20240128193903017
image-20240128194009677

隶属函数的三种确定方法

模糊统计法

用的比较少的模糊统计法

找特别多人

image-20240128194409356

借助已有的客观尺度

合适的指标，并能收集到数据

image-20240128194540182

指派法

有很多分布，主要是梯形分布

image-20240128195038097
image-20240128195025001

例题一

image-20240128195203066

例题二

image-20240128195305070

梯形分布

image-20240128195426402

应用：模糊综合评价

image-20240128195517785

知识点：

确定因素集：相关性之间要不太强

确定评语集：由于每个指标的评价值不同，形成不同的等级。

image-20240128195716703

确定权重：Delphi法，专家法。

无数据：层次分析法

有数据：熵权法

权重也需要归一化，确定的时候注意

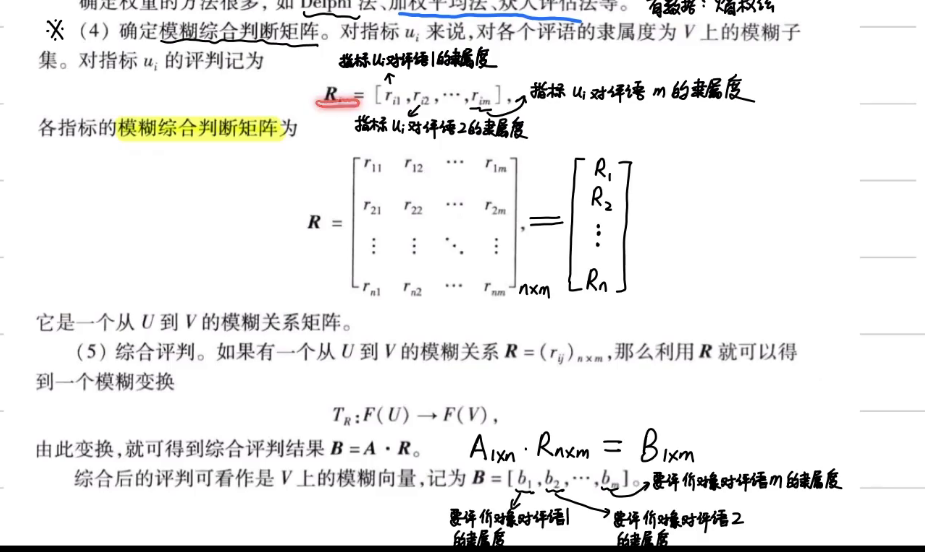
模糊综合判断矩阵

image-20240128200100963image-20240128200131978

解释：第一列表示各个指标对于评语1的隶属度

image-20240128200239957

例题：

image-20240128200407651

层次分析法得到权重

image-20240128200513147
image-20240128200537561

一级模糊综合评价模型例子

一

image-20240128200742371

SO2的隶属度计算

image-20240128200932155

同理：

image-20240128201002529

AR=image-20240128201019735

二

image-20240128201137546
image-20240128201342001
image-20240128201252683

多级模糊综合评价模型的引入

image-20240128202425981
image-20240128202456942
image-20240128202620958
image-20240128202637622

重复1的步骤2遍即可

三极模糊综合评价模型

image-20240128202134589

同理

image-20240128203040666
image-20240128203115836
image-20240128203122965