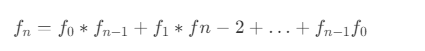ACM-组合数学初步

排列

$ A_n^m=n(n-1)(n-2)(n-m+1)=$

解释：从 n 个中选一个，有 n 种选法，再选第二个，从 n-1 个中选，有 n-1 种选法，以此类推.

组合

$C_n^m=\frac{A_n^m}{m!}=\frac{n!}{m!(n-m)!}$

定义：从 n 个中选择 m 个组成集合其中，不同的集合的数量。

推论

$ +=$

杨辉三角求组合数

#include<cstdio>
const int N = 2000 + 5;
const int MOD = (int)1e9 + 7;
int comb[N][N];//comb[n][m]就是C(n,m)
void init(){
    for(int i = 0; i < N; i ++){
        comb[i][0] = comb[i][i] = 1;
        for(int j = 1; j < i; j ++){
            comb[i][j] = comb[i-1][j] + comb[i-1][j-1];
            comb[i][j] %= MOD;
        }
    }
}
int main(){
    init();
}

二项式定理

$(a+b)^n=\sum_{i=0}^{n}\binom{n}{i}a^{n-i}b^i$

$C_n^0+C_n^1+C_n^2\cdots+C_n^n=(1+1)^n=2^n$

$C_n^0-C_n^1+C_n^2-C_n^3\cdots +C_n^n=(1-1)^n=(0)^n$

Lucas 定理

若 p 是质数，则对于任意整数1≤m≤n有：

$\binom{n}{m} \equiv \binom{n ~ mod ~ p}{m ~ mod ~ p}\binom{n/p}{m/p} (mod~p)$

鸽巢定理

定义：将 n+1 个物体，划分为 n 组，那么有至少一组有两个（或以上）的物体。
推广：将 n 个物体，划分为 k 组，那么至少存在一个分组，含有大于或等于$\lceil \frac{n}{k} \rceil$个物品

例题：给你n个正整数$A=\{a_1,a_2...a_n\}$，和一个正整数 c，问，是否能找到一个 A 的子集 B，B 中元素的和是 c 的倍数，如果能则输出他们的编号。$1 \le c \le n \le 10^5 ,1 \le a_i \le 10^5$

解法：设 A 的前缀和为$sum_i$

若有$若有 sum_l \equiv sum_r~(mod~c)$

即$即 sum_l -sum_r\equiv0 ~(mod~c)$

所以$那么 \sum_{i=l+1}^ra_i\equiv0 ~(mod~c)$即为解

前缀和的个数为n,模c的情况下去除为0的情况，总共有c−1种情况，n>c−1

$根据鸽巢定理一定有 sum_l \equiv sum_r~(mod~c)$

综上所述：$综上所述：该题恒有解，解为\{ a_{l+1},a_{l+2},\cdots ,a_r |sum_l \equiv sum_r~(mod~c) \}$

容斥定理

定义：

设有 n 个集合 $S_i$ , $|S_i|$ 表示 $S_i$ 的大小，有：

$\left| \bigcup_{i=1}^nS_i \right|=\sum_{i=1}^{n}|S_i|-\sum_{1 \le i < j \le n}|S_i\cap S_j|+\sum_{1 \le i < j <k \le n}|S_i\cap S_j\cap S_k|- \cdots$

举例：$|A\cup B\cup C|= |A|+|B|+|C|-|A\cap B|-|A\cap C| -|B\cap C|+|A\cap B\cap C|$

卡特兰(Catalan)数

从零开始，卡特兰数的前几项为1,1,2,5,14,42,132,429,1430,4862,16796,58786,208012,742900,2674440,9694845,35357670,129644790…

定义

递归定义

递推关系

$f_n=\frac{4n-2}{n+1}f_{n-1}$

通项公式

$f_n=\frac{1}{n+1}C_{2n}^{n}$

经化简后可得

$f_n=C_{2n}^{n}-C_{2n}^{n-1}$

只要我们在解决问题时得到了上面的一个关系，那么你就已经解决了这个问题，因为他们都是卡特兰数列

例题1

在一个w×h的网格上，你最开始在(0,0)上，你每个单位时间可以向上走一格，或者向右走一格，在任意一个时刻，你往右走的次数都不能少于往上走的次数，问走到(n,n),0≤n有多少种不同的合法路径。

合法路径个数为$C_{2n}^{n}-C_{2n}^{n-1}$

直接求不好，考虑求有多少种不合法路径

路径总数为在2n次移动中选n次向上移动，即$C_{2n}^{n}$

我们把y=x+1这条线画出来，发现所有的合法路径都是不能碰到这条线的，碰到即说明是一条不合法路径

由于所有的不合法路径一定会与y=x+1有这么一个交点

我们把(a,a+1)之后的路径全部按照y=x+1这条线对称过去这样，最后的终点就会变成(n−1,n+1)

由于所有的不合法路径一定会与y=x+1 我们可以得出，所有不合法路径对称后都唯一对应着一条到(n−1,n+1)的路径且所有到(n−1,n+1)的一条路径都唯一对应着一条不合法路径（只需将其对称回去即可）所以不合法路径总数是

$C_{2n}^{n-1}$

合法：$C_{2n}^{n}-C_{2n}^{n-1}$

01序列

你现在有n个0和n个1，问有多少个长度为2n的序列，使得序列的任意一个前缀中1的个数都大于等于0的个数例如n=2 有1100,10101100,1010两种合法序列而1001,0101,0110,00111001,0101,0110,0011都是不合法的序列

合法的序列个数为$C_{2n}^{n}-C_{2n}^{n-1}$

括号匹配

你有n个左括号，n个右括号，问有多少个长度为2n2的括号序列使得所有的括号都是合法的

合法的序列个数为$C_{2n}^{n}-C_{2n}^{n-1}$

要使所有的括号合法，实际上就是在每一个前缀中左括号的数量都不少于右括号的数量将左括号看做1，右括号看做0，这题又和上面那题一模一样了

进出栈问题

有一个栈，我们有2n次操作，n次进栈，n次出栈，问有多少中合法的进出栈序列

合法的序列个数为$C_{2n}^{n}-C_{2n}^{n-1}$

要使序列合法，在任何一个前缀中进栈次数都不能少于出栈次数……

312排列

一个长度为n的排列a，只要满足i<j<k且$a_j<a_k<a_i$就称这个排列为312排列求n的全排列中不是312排列的排列个数

答案也是卡特兰数

我们考虑312排列有什么样的特征如果考虑一个排列能否被1,2,3,…,n−1,n,排列用进栈出栈来表示那么312排列就是所有不能被表示出来的排列那么这个问题就被转化成进出栈问题了

不相交弦问题

在一个圆周上分布着 2n个点，两两配对，并在这两个点之间连一条弦，要求所得的2n条弦彼此不相交的配对方案数 合法的序列个数为$C_{2n}^{n}-C_{2n}^{n-1}$

这个问题没有上面的问题那么显然，我们规定一个点为初始点，然后规定一个方向为正方向如规定最上面那个点为初始点，逆时针方向为正方向然后我们把一个匹配第一次遇到的点（称为起点）旁边写一个左括号((，一个匹配第二次遇到的点（称为终点）旁边写一个右括号)

在规定了这样的一个顺序后，在任意一个前缀中起点的个数都不能少于终点的个数于是这又是一个卡特兰数列了

凸多边形的三角划分

一个凸的n边形，用直线连接他的两个顶点使之分成多个三角形，每条直线不能相交，问一共有多少种划分方案

答案还是卡特兰数列

我们在凸多边形中随便挑两个顶点连一条边，这个凸多边形就会被分成两个小凸多边形，由于每条直线不能相交，接下来我们就只要求这两个小凸多边形的划分方案然后乘起来即可

和二叉树的构成问题一样，我们枚举大凸多边形被分成的两个小凸多边形的大小即可