编译原理2013

Construct minimum-state DFA for the following regular expression: (a|b)*a

直接画NFA图！

然后NFA转DFA

第一步写空集合

按照a、b、c进行转化，产生新集合！

重复操作，直到没有新集合产生！

然后画出表和图！

img

从NFA到DFA的转换：

	a	b
A={0,1,2,4,7}	B={1,2,3,4,6,7,8}	C={1,2,4,5,6,7}
B={1,2,3,4,6,7,8}	B={1,2,3,4,6,7,8}	C={1,2,4,5,6,7}
C={1,2,4,5,6,7}	B={1,2,3,4,6,7,8}	C={1,2,4,5,6,7}

构造DFA如下图所示：

img

状态	a	b
A={A,C}	B={B}	A={A,C}
B={B}	B={B}	B={C}

最小化

分状态：接收和未接收状态！

然后不断集合内进行判断，看能不能细分！

直到不能细分为止！

img

---

2 [20分] 考虑如下文法：S 是开始符号

Consider the following grammar: S is the start symbol

S → aAbDe  
A → BSD | ε  
B → SAc  
D → De | ε

1. [4pts.] Rewrite the grammar.
2. [6pts.] Construct First and Follow sets for the nonterminals of the grammar.
3. [3pts.] Is the grammar LL(1) ? Give your reason.
4. [7pts.] Construct the LL(1) parsing table for this grammar.

第一问注意左递归

第二问：First集采取左右观察，不要观察少就Ok，有时遇到一些依赖就先写上去，不用慌张！Follow一样采取右观察，看什么时候出现，紧跟在后面的是什么（终结符直接加上去，不是终结符就加上First！），如果是空就要加上左边的Follow！

第三问判断Select会不会相交！（First集加空跟上Follow集）

第四问正常按照Select来画就好了！

---

1) [4pts] 重写文法 / Rewrite the grammar

✅答案：

S → aAbDe  
A → BSD  
A → ε  
B → SAc  
D → D'  
D' → eD'  
D' → ε

🧠解释 Explanation:

为了更清晰地处理 D → De | ε，我们将其左递归改写为右递归形式：

• 把 D → De 改为 D → D'
• 其中 D' → eD' | ε （标准的消除左递归的方法）

---

2) [6pts] 构造 First 和 Follow 集 / Construct First and Follow sets

✅答案：

非终结符	FIRST 集合	FOLLOW 集合
S	{ a }	{ a, b, e, c, $ }
A	{ a, ε }	{ b, c }
B	{ a }	{ a }
D	{ e, ε }	{ b, e, c }
D′	{ e, ε }	{ b, e, c }

产生式 / Production	FIRST 部分	可否推出 ε？	FOLLOW 用于 ε	SELECT 集合
S → aAbDe	FIRST(a) = {a}	否	-	{a}
A → BSD	FIRST(BSD) = FIRST(B) = {a}	否	-	{a}
A → ε	ε	是	FOLLOW(A) = {b, c}	{b, c}
B → SAc	FIRST(S) = {a}	否	-	{a}
D → D′	FIRST(D′) = {e, ε}	是	FOLLOW(D) = {b, c, e}	{e, b, c}
D′ → eD′	FIRST(eD′) = {e}	否	-	{e}
D′ → ε	ε	是	FOLLOW(D′) = {b, c, e}	{b, c, e}

🧠解释 Explanation:

FIRST 集合计算 First Set Explanation:

• FIRST(S) = {a}，因为 S → aAbDe 以终结符 a 开始。
• FIRST(A) = FIRST(BSD) ∪ {ε}。由于 A 有产生式 A → ε，所以 ε ∈ FIRST(A)。而 B → SAc，S → aAbDe，所以最终是 {a, ε}。
• FIRST(B) = FIRST(SAc) = FIRST(S) = {a}
• FIRST(D) = FIRST(De) ∪ {ε}，De 的首符是 e，所以是 {e, ε}
• FIRST(D') = {e, ε}（标准右递归消除左递归形式）

FOLLOW 集合计算 Follow Set Explanation:

• FOLLOW(S) 包括 $（起始符号），也出现在 B 和 A 的产生式中，所以引入了其他非终结符的 First。
• FOLLOW(A) 在 S → aAbDe 中，A 后面是 b，所以 Follow(A) ⊇ {b}，而 bDe 中 D 可空，所以 Follow(A) ⊇ Follow(S)，最终为 {b, c}
• 其他类似推导。

---

3) [3pts] 该文法是 LL(1) 吗？ / Is the grammar LL(1)?

✅答案：

不是 / No

🧠解释 Explanation:

我们计算了每个产生式的 SELECT 集合：

• SELECT(D′ → eD′) = {e}
• SELECT(D′ → ε) = FOLLOW(D′) = {b, c, e}

可以看到它们的交集为 {e}，不为空，违反 LL(1) 要求的 SELECT 集合不相交原则。

所以此文法 不是 LL(1)。

---

4) [7pts] 构造 LL(1) 预测分析表 / Construct the LL(1) parsing table

✅答案：

非终结符	a	b	c	e	$
S	S → aAbDe
A	A → BSD			A → ε
B	B → SAc
D		D → D′	D → D′	D → D′
D′		D′ → ε	D′ → ε	D′ → eD′

🧠解释 Explanation:

• 表中每个条目对应：预测分析表[非终结符][终结符] = 产生式
• 比如 S 遇到 a 时使用产生式 S → aAbDe
• A 在 a 时选 A → BSD，在 e 时选 A → ε
• D′ 的两个产生式 eD′ 和 ε 的 SELECT 集有交集 → 冲突 → 不是 LL(1)

---

LR题

Consider the grammar, E is the start symbol:

(1) E → T * E  
(2) E → a  
(3) T → a

---

✅ 1) [7pts] 构造 LR(0) 项目集的 DFA / Construct the DFA of LR(0) Items

增强文法加画图！

耐心仔细画下去！

我们先加上增强文法（Augmented Grammar）：

(0) E′ → •E
(1) E → •T * E
(2) E → •a
(3) T → •a

img

---

✅ 2) [3pts] 此文法是 LR(0) 文法吗？/ Is this grammar LR(0)?

注意规约-规约冲突！

❌ 答案：不是 / No

🧠 解释 Explanation:

在 状态 I3 中，包含两个归约项：

• E → a• （对应产生式 2）
• T → a• （对应产生式 3）

这两个产生式都将在输入符号为 * 或 $ 时尝试归约，因此发生归约-归约冲突（Reduce-Reduce Conflict）。

👉 因此该文法不是 LR(0)。

---

✅ 3) [5pts] 构造 SLR(1) 分析表 / Construct the SLR(1) Parsing Table

按照上面那个表来构造，有规约的时候看Follow集！

我们使用 FOLLOW 集合来解决 LR(0) 冲突，构造 SLR(1) 表。

---

🔹 FOLLOW 集合计算 / FOLLOW Sets

• FOLLOW(E) = { $ }
• FOLLOW(T) = { * }

---

🔹 分析表（SLR(1) Parsing Table）

状态	a	*	$	E	T	Action
0	S3			1	2
1			acc
2		S4
3		r3	r2			由 FOLLOW(T), FOLLOW(E) 决定
4	S3			5	2
5			r1			FOLLOW(E) = {$}

r1 = E → T * E r2 = E → a r3 = T → a

---

✅ 4) [5pts] 输入串 a*a 的分析过程 / Show the parsing stack for input a*a

按照分析表，给出分析栈，状态栈，符号栈，输入串，动作，GOTO！

我们构建 SLR(1) 分析栈，如课本格式：

步骤	分析栈 (状态+符号)	剩余输入串	动作（Action）	GOTO
1	$0	a * a $	读入 a → S3
2	$0 a3	* a $	归约 T → a → r3	GOTO(0,T)=2
3	$0 T2	* a $	读入 * → S4
4	$0 T2 *4	a $	读入 a → S3
5	$0 T2 *4 a3	$	归约 E → a → r2	GOTO(4,E)=5
6	$0 T2 *4 E5	$	归约 E → T*E→r1	GOTO(0,E)=1
7	$0 E1	$	接受 acc

---

✅ 三地址

给出下列程序的三地址码序列：

Repeat:
    y := y - 1;
    if y > 0 then
        y := y - x
    else
        y := y + x
    end
Until y > x and y < 100;
write y

🚫 不需要给出属性文法（attribute grammar）

---

✅ 2、解答 / Answer

我们将控制结构翻译为三地址码（Three-Address Code）。为方便，我们给每一行编号 100 开始。

---

✅ 三地址码 / Three-Address Code

行号	三地址码 / Three-Address Code	中文说明 / Explanation in Chinese
100	y := y - 1	y 自减 1
101	if y > 0 goto 104	如果 y > 0，跳转执行 then 分支
102	y := y + x	else 分支：y 加上 x
103	goto 105	执行完 else 分支后跳转出 if 语句
104	y := y - x	then 分支：y 减去 x
105	if y <= x goto 100	条件一不满足：y ≤ x，继续 Repeat 循环
106	if y >= 100 goto 100	条件二不满足：y ≥ 100，也继续 Repeat 循环
107	write y	条件都满足，跳出循环，输出 y

---

✅ 结构解释 / Structure Explanation

• Repeat–Until 结构：循环体先执行，再根据条件判断是否继续。用条件反转（if not condition goto Repeat）实现。
• if–then–else：编译为条件跳转（if...goto）+ 无条件跳转（goto）结构。

---

✅ 翻译逻辑说明 / Translation Logic Summary (中英文)

语句 / Statement	三地址码翻译 / Translation
Repeat: y := y - 1	100: y := y - 1
if y > 0 then y := y - x else y := y + x	条件跳转结构（101–104）
Until y > x and y < 100	条件反转为：若 y ≤ x 或 y ≥ 100 则继续循环（105–106）
write y	最后一条语句输出 y（107）

---

✅ 最终三地址码汇总 / Final Three-Address Code

100: y := y - 1
101: if y > 0 goto 104
102: y := y + x
103: goto 105
104: y := y - x
105: if y <= x goto 100
106: if y >= 100 goto 100
107: write y

---

✅ 综合题

The following chart describes what phases are normally found in a compiler. Fill in the blanks from A to E

---

📘 1）[5pts] 编译器阶段填空 / Compiler Phases Fill-in-the-Blanks

图中描述编译器的主要阶段，填空如下：

img

空格 / Blank	答案 / Answer	解释 / Explanation
A	Syntax Analyzer 语法分析器	分析语法结构，如表达式、语句等
B	Syntax Tree 语法树	抽象表示程序结构的树型形式
C	Semantic Analyzer 语义分析器	分析含义，如类型检查、作用域检查等
D	Target-machine Code 目标代码	最终输出的机器指令或汇编代码
E	Symbol Table 符号表	存储变量、函数等标识符的信息

---

📘 2）[5pts] 正则表达式 / Regular Expression

题目：Σ = {a, b, c}，要求生成“只包含一个 b”的所有字符串。

✅ 答案：

(a|c)* b (a|c)*

🧠 解释 Explanation：

• (a|c)* 表示除了 b 以外任意数量的字符；
• 中间放一个 b；
• 结尾再接任意个 a 或 c，确保只有一个 b。

---

📘 3）[5pts] 左因子提取 / Left Factoring

原文法： A → aAd | aAb | ε 左因子提取后：

✅ 答案：

A->aAA’|ε
A’->d|b

---

📘 4）[6pts] 右推导与句柄识别 / Rightmost Derivation & Handles

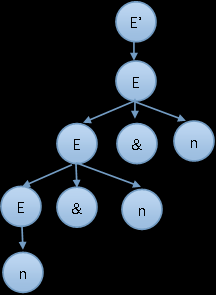
文法： E' → E E → E & n | n

目标串： n & n & n

✅ Rightmost derivation / 右推导：

E'  
⇒ E  
⇒ E & n  
⇒ E & n & n  
⇒ n & n & n

✅ 各步的右句型、可接受前缀（viable prefix）、句柄（handle）：

步骤 / Step	右句型 / Right Sentential Form	Viable Prefix	Handle
1	E		E
2	E & n	E &	E & n
3	E & n & n	E & n &	E & n
4	n & n & n	n & n &	n

🧠 解释 Explanation：

• 每次最右边的 n 是句柄；
• 可接受前缀是栈中内容，即移进过的部分。

---

📘 5）[4pts] 属性文法与依赖图 / Attribute Grammar and Dependency Graph

文法：

S → (L)      {S.h = L.h × 2}  
S → a        {S.h = 1}  
L → L(1), S  {L.h = L(1).h + S.h}  
L → S        {L.h = S.h}

输入串： (a,a)

img