编译原理CH2要点

1. 文法、语法制导翻译方案、语法制导的翻译器

以一个仅支持个位数加减法的表达式为例：

文法：

1 2	list -> list + digit \| list - digit \| digit digit -> 0 \| 1 \| … \| 9

消除了左递归的语法制导翻译方案：

1
2
3

expr -> term rest
rest -> + term { print('+') } rest | - term { print('-') } rest | ε
term -> 0 { print('0') } | 1 { print('1') } | … | 9 { print('9') }

解释：

expr 表示一个表达式，它由一个 term 和可能跟随的加减操作（通过 rest 实现）。
rest 处理加法和减法，并打印相应的操作符（+ 或 -）。
term 对应于单个数字（digit），并打印该数字。

语法制导翻译器：

class Translator {
    void translate(Expr expr) {
        // 具体的翻译过程
    }
}

在 translate 方法中，我们会根据文法规则生成对应的输出。例如，遇到一个加法操作时，会执行相应的打印操作来输出 +。

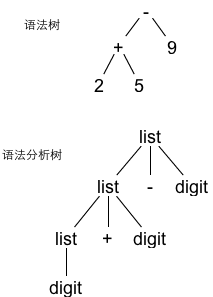
2. 语法树、语法分析树

以 2 + 5 - 9 为例：

3. 正则文法、上下文无关文法、上下文相关文法

文法缩写：

RG：正则文法
CFG：上下文无关文法
CSG：上下文相关文法

正则文法 (RG):

产生式的右手边满足以下形式之一：
- B -> a
- B -> a C
- B -> ε
特点： 只需要记录当前状态即可，适用于有限状态自动机（DFA）。

上下文无关文法 (CFG):

产生式的右手边可以是任意组合的终结符和非终结符。
特点： 适用于下推自动机（PDA），可以匹配更复杂的结构，如括号匹配。

上下文相关文法 (CSG):

产生式左手边可以包含终结符和非终结符，右手边可以是任意组合。
特点： 可以处理需要上下文信息的语言，但更复杂。

总结：

RG：对应有限状态自动机，适合简单的模式匹配。
CFG：对应下推自动机，适合更复杂的结构，如编程语言的语法。
CSG：比 CFG 更灵活，能够处理更复杂的上下文关系。

4. 为什么有 n 个运算符的优先级，就对应 n+1 个产生式？

优先级分析：

在文法中，处理优先级的方式之一是通过引入额外的产生式来“层次化”运算符。
假设有 n 个优先级，则需要 n+1 个产生式来分别处理不同优先级的操作符。
例如，四则运算文法中，乘除法（优先级高）会更早地出现在语法树的底部，而加减法（优先级低）则会靠近根部。

解释：

通过调整产生式的顺序和优先级，可以确保运算符的顺序按照数学规则正确执行。
例如，乘除法的产生式通常在加减法之前，从而保证乘除法优先计算。

5. 避免二义性文法的有效原则

二义性文法：

在上下文无关文法 (CFG) 中，如果一个输入字符串可以通过两种不同的语法树（或推导过程）来生成，那么这个文法就是二义性的。二义性的问题主要出现在选择结构（|）中，特别是多个规则有相同的前缀时，会导致不同的解析方式。

避免二义性的原则：

明确优先级： 在文法中定义明确的优先级，可以避免二义性。一个常见的方法是给不同的操作符设定优先级，并且确保文法的规则能正确区分优先级不同的操作。
避免共同前缀： 如果多个规则的右侧有共同的前缀，可能会导致二义性。解决方法是进行文法改写，将共同前缀提取出来，使用新的规则来消除这种情况。

PEG（Parsing Expression Grammar）：

PEG 是一种类似于 CFG 的文法类型，但它是 无二义性的。在 PEG 中，选择结构（|）是有顺序的，选择的优先级由左到右进行解析，因此不会出现二义性问题。这使得 PEG 的解析更加明确和直接。

总结：

在避免二义性时，首先需要确保文法中没有不必要的选择冲突或共同前缀。通过合理的优先级设计和避免选择的重复前缀，可以使文法变得无二义性。

6. 避免预测分析器因左递归文法造成的无限循环

左递归文法：

左递归 是指文法中某个非终结符在其产生式右边直接或间接地调用自己，导致递归调用无法结束。

例如：
1
A -> A x | y
在这个产生式中，A 会直接或间接调用自己，导致预测分析器进入无限循环。

语法制导翻译伪代码：

void A(){
    switch(lookahead){
        case x:
            A(); match(x); break;
        case y:
            match(y); break;
        default:
            report("syntax error");
    }
}

当输入符合 A -> A x 规则时，调用 A() 会导致死循环，因为 A() 又会再次调用自己。

解决方法：

可以通过消除左递归，将文法改为 非左递归形式。例如，将上面的 A -> A x | y 改写为：
1
2
B -> y C
C -> x C | ε
这样，我们通过引入新的非终结符 B 和 C 来消除左递归，避免了无限循环的问题。

总结：

左递归文法 会导致预测分析器进入死循环，需要将其改写为 非左递归形式。通过引入辅助的非终结符来消除左递归，可以使预测分析器正常工作。

7. 为什么在右递归的文法中，包含了左结合运算符的表达式翻译会比较困难？

右递归与左结合运算符：

右递归 是指文法规则中，非终结符在右侧出现，并且递归地引用自己。与之相对的是左递归，左递归在文法中较容易处理，但右递归如果应用到包含 左结合运算符 的表达式时，可能会导致翻译上的困难。

左结合运算符（例如加法）：

左结合运算符的特点是，多个相同的运算符按从左到右的顺序进行运算。举个例子，在表达式 2 + 3 + 4 中，运算顺序是 (2 + 3) + 4。

问题：

在 右递归 的文法中，运算符的结合顺序是从右到左的，这和左结合运算符的自然顺序不一致。这样，翻译出来的语法树或中间代码的结构就可能和预期不符。

解决办法：

在这种情况下，翻译时需要考虑如何调整递归的方式，或者使用其他方法（例如将文法改写为合适的形式）来保证运算顺序符合预期。

总结：

右递归文法对于左结合运算符的表达式翻译较为复杂，因为右递归会产生从右到左的运算顺序，而左结合运算符通常需要从左到右的顺序。需要调整文法或翻译策略来解决这个问题。

8. 中间代码生成时的左值和右值问题

左值和右值：

左值（lvalue）是可以出现在赋值语句左侧的对象，它表示存储位置，可以被修改。
右值（rvalue）是一个值，它通常出现在赋值语句的右侧，表示一个计算结果或常量。

lvalue() 和 rvalue() 的伪代码：

lvalue() {
    // 处理左值，返回一个可修改的对象
}

rvalue() {
    // 处理右值，返回一个计算结果
}

为什么不能直接用 value()？

lvalue() 和 rvalue() 分别处理左值和右值的不同情况。左值和右值的处理方式不同：左值表示一个存储位置，右值表示一个计算结果或常量。
value() 函数无法区分左值和右值的语法语义差异，因此不能直接使用。我们需要分别处理左值和右值，以保证正确的中间代码生成。

总结：