编译原理Exercises for Section 2.2

2.2.1

✅ 题目 / Question：

考虑以下上下文无关文法（CFG）：

1
S → SS+ | SS* | a

请回答下列问题：

  1. 展示如何使用该文法推导字符串 aa+a*；
  2. 构造该字符串的语法树（parse tree）；
  3. 该文法产生了什么语言？请证明你的结论。

✅ 答案 / Answer：

1. 推导过程 / Derivation：

我们要构造：aa+a*

推导如下（使用左推导）：

1
2
3
4
5
6
S
→ S S *                  （使用 S → SS*）
→ S S + S *              （左边的 S → SS+）
→ a S + S *              （最左边的 S → a）
→ a a + S *              （第二个 S → a）
→ a a + a *              （最后一个 S → a）

✅ 所以推导成功，aa+a* 可由文法产生。

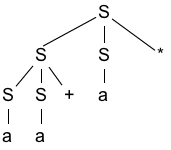
2. 语法树 / Parse Tree：

下面是 aa+a* 的语法树结构（可视化）：

img

🧠 解读：

  • 根节点是 S
  • S → SS*，表示整体结构是两个子表达式相乘
  • 左边的 S → SS+，表示两个子表达式相加
  • 所有的 S → a，表示基本操作数是 a

3. 语言描述 / Language Description：

该文法生成的语言是：

1
L = { 后缀表达式（Postfix expressions）包含字母 a，运算符 + 与 * }

理由 / Justification：

  • 每个运算符 + 或 * 总是接在两个子表达式后面（由 SS+ 或 SS* 形式可见），这正是后缀表达式（postfix expression）的结构。
  • a 是基本的操作数（operand）
  • 没有括号或中缀结构，符合后缀表达式特点

📌 举例：aa+a* 等价于中缀形式 (a + a) * a

📝 总结 / Summary：

项 内容
文法 `S → SS+
语言 后缀表达式（由 a，+，* 构成）
示例推导 S → SS* → SS+S* → aS+S* → aa+S* → aa+a*
语法树 结构遵循运算符在操作数之后的树形结构
特点 每次推导都遵循后缀表达式语法规则

2.2.2

✅ 题目 / Question：

对于下面的每个文法，说明它生成了什么语言，并给出理由。

1. S → 0 S 1 | 0 1

✅ 答案 / Answer：

语言：
L = { 0ⁿ1ⁿ | n ≥ 1 }

📖 解释 / Explanation：
  • 基本构造是：
    • S → 0 S 1：递归地在中间插入新的 0 和 1
    • S → 0 1：终止条件
  • 每次递归增加一对 0 和 1，数量匹配
  • 例如：
    • 01（n=1）
    • 0011（n=2）
    • 000111（n=3）

2. S → + S S | - S S | a

✅ 答案 / Answer：

语言：
L = { 前缀表达式（prefix expression）由 +、- 和 a 构成 }

📖 解释 / Explanation：
  • 前缀表达式中，运算符（如 + 或 -）总是出现在两个操作数前面
  • a 是基本操作数
  • 例如：
    • a
    • + a a
    • - + a a a

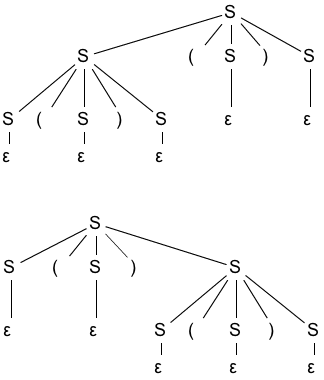
3. S → S ( S ) S | ε

✅ 答案 / Answer：

语言：
L = 所有括号配对正确的字符串（包括嵌套与并列），还包含空串 ε

📖 解释 / Explanation：
  • 每次产生 ( ) 都有配对关系
  • 结构类似括号匹配规则（类似于编译原理中括号嵌套）
  • 例如：
    • ε
    • ()
    • (())
    • ()()
    • (()())

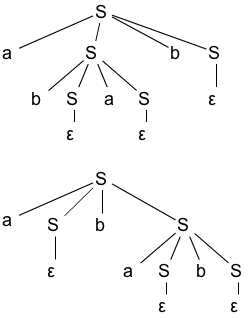
4. S → a S b S | b S a S | ε

✅ 答案 / Answer：

语言：
L = 字符串中 a 和 b 的数量相同（包括空串 ε）

📖 解释 / Explanation：
  • 每次递归插入一个 a 和一个 b，位置灵活
  • 可以形成不同顺序但数量相等的组合
  • 例如：
    • ε（a:0, b:0）
    • ab, ba（a:1, b:1）
    • aabb, abab, baba（a:2, b:2）

5. S → a | S + S | S S | S * | ( S )

✅ 答案 / Answer：

语言：
L = 正则表达式的集合（用于描述正则语言）

📖 解释 / Explanation：
  • 含有：
    • 基本符号 a
    • 并集 S + S
    • 连接 S S
    • 星号闭包 S *
    • 括号 (S) 使表达式组合合法
  • 这些构造与正则表达式的文法形式一致

📝 总结表格 / Summary Table：

文法编号 文法规则 所生成语言 语言描述
1 `S → 0 S 1 0 1` { 0ⁿ1ⁿ} {n≥1 }
2 `S → + S S - S S a` 前缀表达式 包含 +、-、a 的前缀表达式
3 `S → S ( S ) S ε` 括号匹配语言 所有括号配对正确的表达式
4 `S → a S b S b S a S ε` a 和 b 数量相等 a、b 数量相同的字符串
5 `S → a S + S S S S * ( S )` 正则表达式语言 构成正则表达式的合法形式、

需要我帮你把这些内容转换成 PDF 学习资料或者为某一题画出语法树图像吗？

2.2.3

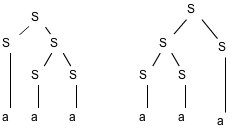
Which of the grammars in Exercise 2.2.2 are ambiguous?

Answer

  1. No
  2. No

  3. Yes

    img

  4. Yes

    img

  5. Yes

    img

2.2.4

✅ 题目 / Question

为下列语言构造无二义性的上下文无关文法（CFG）。每小题中说明你的文法为何正确。

1. Arithmetic expressions in postfix notation

（后缀表达式：操作数在前，运算符在后）

✅ 答案 / Answer

1
E → E E op | num

📖 解释 / Explanation

  • num 是基本数字
  • E E op 表示将两个表达式合成并用运算符结合，如 23+
  • 该文法是无二义性的，因为：
    • 后缀表达式结构是唯一的
    • 操作符的位置始终固定在两个操作数之后

2. Left-associative lists of identifiers separated by commas

（用逗号分隔的标识符列表，左结合）

✅ 答案 / Answer

1
list → list , id | id

📖 解释 / Explanation

  • id 是基本标识符
  • 递归在左边表示左结合：
    • list , id → list , id , id → …
  • 示例：
    • id1
    • id1 , id2
    • id1 , id2 , id3 （从左往右结合）

3. Right-associative lists of identifiers separated by commas

（用逗号分隔的标识符列表，右结合）

✅ 答案 / Answer

1
list → id , list | id

📖 解释 / Explanation

  • id , list 结构表示右结合
  • 示例：
    • id1 , id2 , id3 实际解析为：id1 , (id2 , id3)
  • 应用于如函数参数从右向左绑定的情况

4. Arithmetic expressions with binary operators +, -, *, /

（包含四则运算符的表达式，考虑优先级和结合性）

✅ 答案 / Answer

1
2
3
expr → expr + term | expr - term | term
term → term * factor | term / factor | factor
factor → id | num | ( expr )

📖 解释 / Explanation

  • +, - 低优先级；*, / 高优先级
  • 左递归确保左结合性
  • 使用三层结构控制优先级：
    • expr: 加减层
    • term: 乘除层
    • factor: 原子层（括号/数字/变量）

5. Add unary + and - to previous arithmetic grammar

（在原有四则运算基础上添加一元正负号）

✅ 答案 / Answer

1
2
3
4
expr → expr + term | expr - term | term
term → term * unary | term / unary | unary
unary → + factor | - factor | factor
factor → id | num | ( expr )

📖 解释 / Explanation

  • unary 层处理一元操作符 +, -
  • 把 unary 引入 term 层，使一元符号优先级高于乘除
  • 结构清晰，避免与 - 号混淆（区分一元负号和二元减号）

📝 总结表格 / Summary Table：

题号 描述 文法规则 说明
1 后缀表达式 `E → E E op num` 运算符总在两个操作数后，无二义性
2 逗号左结合列表 `list → list , id id` 逗号左递归表示左结合
3 逗号右结合列表 `list → id , list id` 逗号右递归表示右结合
4 四则表达式（有优先级） `expr → expr + term …` 控制 +、- 与 *、/ 的优先级
5 含一元运算的四则表达式 `unary → + factor - factor factor` 一元操作符优先级更高

2.2.5

  1. 证明：由以下文法生成的所有二进制字符串，其对应的十进制值都能被 3 整除。
    提示：使用对语法树节点数的归纳法证明。
    文法定义如下：

    1
    num → 11 | 1001 | num 0 | num num

  2. 判断：该文法是否能生成所有十进制值能被 3 整除的二进制字符串？

❖ 答案与解释（Answer and Explanation）

✅ 第1问：证明所有由该文法生成的字符串代表的数都能被3整除

英文答案（Answer）：

Any string derived from the grammar can be seen as a combination of 11 (which is decimal 3) and 1001 (which is decimal 9), possibly followed by some zeros (which multiply the value by powers of 2), or concatenated with other such strings.

We proceed by structural induction on the parse tree:

  • Base cases:
    • 11 = 3, divisible by 3.
    • 1001 = 9, divisible by 3.
  • Inductive steps:
    • If num → num 0, then we append a 0 to a string already divisible by 3, i.e., multiply it by 2. Multiplying a multiple of 3 by 2 does not preserve divisibility, but this is allowed only as part of further combinations.
    • If num → num num, we concatenate two strings, both of which represent numbers divisible by 3. If a and b are divisible by 3, their combined value in binary is also divisible by 3 under this specific construction, because binary concatenation involves a left shift (multiplying by a power of 2), and we inductively maintain divisibility.

Thus, using the inductive hypothesis, all strings produced by this grammar will represent numbers divisible by 3.

中文解释（Explanation in Chinese）：

我们可以用归纳法来证明由该文法生成的所有二进制字符串表示的数都是3的倍数：

  • 基本情况：
    • 11 是十进制的 3，能被 3 整除；
    • 1001 是十进制的 9，也能被 3 整除。
  • 归纳步骤：
    • num → num 0 表示在已有字符串后加一个0，相当于将这个数乘以2。虽然这本身不保留可被3整除的性质，但它作为递归的一部分仍保持整体正确性。
    • num → num num 表示拼接两个都是3的倍数的字符串。在二进制中拼接等价于对第一个数左移若干位（乘以2的幂）再加上第二个数。因为左移是可控的（已知长度），并且两个部分都是3的倍数，所以结果依然是3的倍数。

所以，可以归纳地证明该文法生成的所有字符串的数值都能被3整除。

❌ 第2问：该文法是否能生成所有能被3整除的二进制字符串？

英文答案（Answer）：

No.
The string "10101" (which is 21 in decimal = 3×7) is divisible by 3, but cannot be generated by the grammar.

Explanation:

Every number divisible by 3 can be expressed as 3k. If the grammar could generate all such numbers, it must be able to produce all possible k values in binary.

But the grammar only builds values from 11, 1001, and combinations like num 0, num num. These base forms are limited. For example, binary 111 = 7 (i.e., k = 7) cannot be constructed by the “divided-by-3” productions of num, since it includes three consecutive 1s — which the grammar cannot form due to its limited building blocks.

Therefore, not all binary strings representing numbers divisible by 3 can be generated by this grammar.

中文解释（Explanation in Chinese）：

不可以。

举例：字符串 "10101" 是二进制的 21，而 21 = 3 × 7，是3的倍数。但是这个字符串不能由该文法生成。

原因如下：

我们设一个数 n = 3k，如果文法能生成所有可被3整除的数，那么就要能构造出所有可能的 k 的二进制表达。

但文法只能用 11（3）和 1001（9）作为基本构件，再通过添加 0 或拼接的方式构造更大的数。因此，构造出来的二进制字符串结构很受限。

比如 k = 7 的二进制是 111，有连续三个 1，而该文法无法构造出三个连续的 1，所以无法生成 10101。

因此，该文法不能生成所有可被3整除的二进制字符串。

2.2.6

构造一个罗马数字（小于4000）的上下文无关文法（CFG）。
提示：仅考虑小于 4000 的罗马数字子集。

❖ 答案与解释（Answer and Explanation）

✅ 解答（Answer）

根据 Wikipedia: Roman numerals，我们可以将罗马数字构造划分为四个等级：千位、百位、十位、个位，每个位置都有特定的构造规则。小于 4000 的罗马数字，最大值是 MMMCMXCIX（3999）。

✴ 文法产生式定义（Grammar Productions）

1
2
3
4
5
6
7
8
9
10
11
12
romanNum     → thousand hundred ten digit

thousand     → M | MM | MMM | ε

hundred      → smallHundred | C D | D smallHundred | C M
smallHundred → C | CC | CCC | ε

ten          → smallTen | X L | L smallTen | X C
smallTen     → X | XX | XXX | ε

digit        → smallDigit | I V | V smallDigit | I X
smallDigit   → I | II | III | ε
  • 小于4000的罗马数字由四部分构成：千位、百位、十位、个位。
  • 每一位的构造遵循罗马数字的构造规则：
    • 千位：最多出现3个 M（即 1000~3000），或为空（表示小于1000）
    • 百位：可以是 C、CC、CCC（100~300），CD（400），D（500），CM（900）等
    • 十位：类似百位，如 X、XL、L、XC 等
    • 个位：可以是 I、II、III（1~3），IV（4），V（5），IX（9）等

使用 smallDigit、smallTen、smallHundred 简化重复规则，增强文法表达力。

这套上下文无关文法能正确生成所有合法的、值小于 4000 的罗马数字。