计组习题的那些事(6)
计组习题的那些事(6)
今天起床,感觉十分通透啊,是个不错的日子!!!
流水线其实还是有点意思的,出现问题了,不断的去寻找方案解决,要么调整做的方式,要么做一些其他的事情,想的都是怎么更有效率的达到最后的目标。
这一章节我很不擅长,还是需要专注一些,重点在于缓存,RAM和页表那里。
问题
考虑由SDRAM芯片构造的主存,数据以脉冲串的形式传输(脉冲长度为8),并行传输32位数据,时钟频率为400MHz,要求计算传输以下数据量分别需要的时间以及对应的延迟: (a) 32字节数据; (b) 64字节数据。
答案
- 传输时间:13个时钟周期,换算成时间为32.5ns。
- 延迟:5个时钟周期,换算成时间为12.5ns。
- 传输时间:23个时钟周期,换算成时间为57.5ns。
- 延迟:5个时钟周期,换算成时间为12.5ns。
问题
对于一个使用512K×8存储器芯片的8M×32存储器,要求描述一种类似于图8-10的结构。
答案
所需的结构本质上与图8-10中的一样,只是需要16行、每行有4个512K×8的芯片。地址线A₀需要连接到所有的芯片上,地址线A₁连接到一个4位的译码器上,以选择16行中的一行。
解释
- 关于芯片数量及行数的确定: 首先分析存储器容量相关情况,已知要构建的是8M×32的存储器,而使用的是512K×8的存储器芯片。计算可得,总存储单元数量上,8M(8×1024×1024)除以512K(512×1024)等于16,说明在地址维度上需要16个这样的芯片组合来达到8M的地址范围要求;在数据宽度维度上,目标存储器是32位,而芯片是8位,32÷8 = 4,意味着每行需要4个芯片并行才能实现32位的数据宽度。所以综合起来就是需要16行,每行有4个512K×8的芯片来构建这个8M×32的存储器。
- 关于地址线连接方式的解释: 地址线的连接对于芯片的正确寻址非常关键。地址线A₀需要连接到所有的芯片上,这是因为A₀这根地址线用于在每个芯片内部进行更细粒度的单元选择,不管是哪一行的芯片,其内部存储单元的选择都需要用到这根地址线,所以要全部连接。而地址线A₁连接到一个4位的译码器上,是因为要从16行芯片中选择其中一行来进行操作,通过4位译码器(2⁴ = 16种状态)可以刚好实现对16行芯片的准确选择,使得根据不同的地址输入能够准确地定位到具体某一行的芯片,进而配合其他地址线以及芯片内部的地址译码等机制来准确读写相应存储单元的数据。
问题
- 一个计算机系统使用32位的存储器地址,主存有1G字节,有一个4K字节的高速缓存,按组相联的形式组织,每组4个块,每块64个字节,需要计算主存地址中的Tag、Set和Word字段的位数。
- 假设高速缓存初始为空,处理器从位置0开始的连续字单元中取1088个字(每个字4个字节),然后再重复这个取操作序列9次。已知高速缓存比主存快10倍,使用LRU算法进行块替换,估算使用高速缓存后性能提高的倍数。
答案
- Tag字段为22位,Set字段为4位,Word字段为6位。
- 使用高速缓存后性能提高的倍数约为2.15。
解释
(a) 各字段位数计算解释
- Word字段位数计算: 因为一个块有64个字节,按照字节编址,要确定块内具体的字节位置(也就是字单元位置,这里每个字4个字节,但计算字节位置思路相同),需要的位数就是\(log_2{64}\)$ = 6$位,所以Word字段为6位。
- Set字段位数计算: 每组包含的字节数为\(4×64 = 256\)字节,而高速缓存总共有\(4K\)(\(4×1024\))字节,那么高速缓存总共的组数为\(4×1024÷256 = 16\)组,要对这16组进行区分选择,所需要的位数就是\(log_2{16}\)$ = 4$位,所以Set字段需要4位。
- Tag字段位数计算: 已知存储器地址是32位,已经确定了Set字段占4位,Word字段占6位,那么剩下的位数就是Tag字段的位数,即\(32 - 4 - 6 = 22\)位,所以Tag字段为22位。
(b) 性能提高倍数计算解释
分析取操作及缓存块替换情况: 首先,\(1088\)个字,每个字\(4\)个字节,换算成块的数量就是\(1088×4÷64 = 68\)个块,这些块在主存中占用块\(0\)到块\(67\)。高速缓存一共有\(64\)块空间(每组\(4\)个块,共\(16\)组),在第一遍取操作时,把块\(0\)到块\(63\)读入高速缓存后缓存就满了。后续编号为\(64\)到\(67\)的这\(4\)块会映射到第\(0\)、\(1\)、\(2\)和\(3\)组中,并且会按照LRU算法替换所在组中最近最少使用的块(例如在第\(0\)组就替换块\(0\))。 随着后续重复取操作,会出现类似块不断相互替换的情况,比如主存块\(0\)、\(16\)、\(32\)、\(48\)和\(64\)等会竞争高速缓存中第\(0\)组的\(4\)个块位置,不断彼此替换。最后\(12\)个组(第\(4\)组到第\(15\)组)中的主存块在第一遍被取出一次后,在接下来的\(9\)遍中能一直保持在高速缓存中。
计算无缓存和有缓存时的时间: 设高速缓存的访问时间为\(T\),无高速缓存时,每次访问主存,总共要进行\(1088×10\)次访问(取\(1088\)个字,重复\(10\)次),那么总时间就是\(10×68×10T\)(\(68\)个块,每个块访问时间是\(10T\),重复\(10\)次操作)。 有高速缓存时,第一遍取操作需要从主存取\(68\)个块,时间为\(68×11T\)(每个块从主存取到缓存再访问,算\(11T\),\(10T\)是主存访问时间,\(T\)是缓存访问时间),后面\(9\)遍操作中,每遍有\(20\)个块要从主存取(前面分析得出),\(48\)个块能从缓存取,所以时间为\(9(20×11T + 48T)\),那么有高速缓存时总的时间就是\(1×68×11T + 9(20×11T + 48T)\)。
计算性能提高倍数: 根据性能提高倍数的计算公式,用无高速缓存时的时间除以有高速缓存时的时间,即\(\frac{10×68×10T}{1×68×11T + 9(20×11T + 48T)}\),经过计算得出结果约为\(2.15\),这就表明使用高速缓存后性能相比没有高速缓存时有了一定程度的提升,同时也体现出在这种特定取操作及LRU算法下的缓存使用效果以及LRU算法存在的一些在程序循环执行场景下的缺点(导致部分块频繁替换,影响性能提升幅度等)。
问题
- 已知一个由32位的数组成的1024×1024数组,虚拟存储器中每页包含4K字节,主存的1M字节被分配用来存储数组数据,假定发生页故障时从磁盘装载一个页到主存需要10毫秒,假设一次处理该数组的一列,且数组元素按列顺序存储在虚拟存储器中,求会发生多少次页故障以及需要多长时间才能完成这个标准化过程。
- 假设元素按行顺序存储,重复(a)中求页故障次数以及完成标准化过程所需时间的问题。
- 当数组按行顺序存储在存储器中时,提出另一种处理这个数组的方法,估算页故障的次数以及该解决方案所需要的时间。
答案
- 会发生1024次页故障,完成标准化过程需要10.24秒。
- 会发生1024×1024×2次页故障,处理时间为20972秒(约5.8小时)。
- 采用新方法会发生2048次页故障,处理时间为20.48秒。
解释
(a) 按列顺序存储情况解释
- 计算每页可容纳元素个数及主存可容纳页数: 因为每个32位的数是4字节,而每页包含4K字节(4×1024字节),所以每页能容纳的元素个数为\(4×1024÷4 = 1024\)个。主存用于存储数组数据的1M字节(1×1024×1024字节)空间,其包含的页数为\((1×1024×1024)÷(4×1024) = 256\)页。
- 分析页故障次数及处理时间: 由于每一列存储在一页中,每次将一列放到主存中就会产生一次页故障,而数组一共有1024列,所以总共会发生1024次页故障。又已知处理一次页故障需要10毫秒,那么完成这个标准化过程所需时间就是页故障次数乘以每次处理的时间,即\(1024×10\)毫秒 = 10.24秒。
(b) 按行顺序存储情况解释
- 分析处理过程中的页故障情况: 每一列的处理需要两遍,第一遍找最大元素,第二遍执行标准化。当处理第一列时,访问每个元素都会导致一次页故障,并且每访问一个元素会将相应行的所有元素都装入主存中。因为主存只有256页空间,当检查完256个元素后,主存就满了,后续再访问元素就会导致页故障并替换主存中已有的数据,如此重复。这意味着数组中每一个元素的每一次访问都会发生一次页故障,而数组元素总共有\(1024×1024\)个,处理两遍,所以总的页故障次数就是\(2×1024×1024\)次。
- 计算处理时间: 每次页故障处理时间是10毫秒,那么总的处理时间就是页故障次数乘以每次处理时间,即\(2×1024×1024×10\)毫秒 = 20972秒,换算后约为5.8小时。
(c) 新处理方法情况解释
- 阐述新方法及原理: 提出的新方法是在第一遍中先完成每一列的1/4,然后再处理第二个1/4,以此类推,第二遍同样采用这样的方式处理。这样做的好处是可以相对更合理地利用主存空间,减少不必要的页替换导致的频繁页故障。
- 分析页故障次数及处理时间: 通过数组的每一遍会导致1024次页故障,一共处理两遍,所以总共的页故障次数就是\(2×1024 = 2048\)次。每次页故障处理时间是10毫秒,那么处理时间就是\(2048×10\)毫秒 = 20.48秒。 最后通过这个例子整体说明了在主存容量不足以存放应用程序的情况下,页故障次数会显著增加,这种现象被称为系统颠簸(thrashing),体现了存储布局及处理方式对系统性能(这里体现为页故障次数和处理时间)的重要影响。
问题
- 已知磁盘的平均寻道时间为6毫秒,平均旋转延迟为3毫秒,所访问块的平均大小为8K字节,从磁盘传输数据的速率为34M字节/秒,假设这些数据块随机分布在磁盘上,需要估算寻道操作和旋转延迟所占总时间的平均百分比。
- 重新排列磁盘访问,使得在90%的情况中下一次访问的数据块与这次访问的数据块在同一个柱面上,在此情况下重复(a)中估算百分比的问题。
答案
- 寻道操作和旋转延迟所占总时间的平均百分比为97%。
- 寻道操作和旋转延迟所占总时间的平均百分比为92%。
解释
(a) 部分解释
- 计算传输数据块时间: 首先,根据所给的从磁盘传输数据的速率以及数据块大小来计算传输一个数据块需要花费的时间。已知所访问块的平均大小是8K字节(8×1024字节),从磁盘传输数据的速率为34M字节/秒(34×1024×1024字节/秒),根据时间 = 数据量÷传输速率,可得传输一个数据块的时间为\(8×1024÷(34×1024×1024)\)秒,换算成毫秒就是\(8×1024÷(34×1024×1024)×1000\)≈0.23毫秒。
- 计算访问数据块总时间及百分比: 访问每个数据块所需的总时间是由寻道时间、旋转延迟时间以及传输数据块的时间这三部分组成的。已知平均寻道时间为6毫秒,平均旋转延迟为3毫秒,传输一个数据块时间约为0.23毫秒,那么总时间就是\(6 + 3 + 0.23 = 9.23\)毫秒。寻道和旋转延迟这两部分的时间总和是\(6 + 3 = 9\)毫秒,所以它们所占总时间的比例就是\(9÷9.23\)≈0.97,也就是97%。
(b) 部分解释
- 分析重新排列后的访问时间情况: 当重新排列磁盘访问,使得90%的情况中下一次访问的数据块与这次访问的数据块在同一个柱面上时,意味着在这90%的情况里,就不需要进行寻道操作了(因为在同一个柱面,磁头不用移动去寻找磁道了),只需要考虑旋转延迟就行。而还有10%的情况是按照常规的寻道、旋转延迟以及传输数据块的完整流程来的。
- 计算访问一个数据块的平均时间: 根据上述分析,访问一个数据块的平均时间计算如下:90%的情况只需要旋转延迟3毫秒,这部分时间就是\(0.9×3\)毫秒;10%的情况需要完整的寻道、旋转延迟以及传输数据块的时间,也就是$0.1×(6 + 3 )毫秒,把这两部分相加,可得平均时间为\(0.9×3 + 0.1×(6 + 3 )+ 0.23 = 3.89\)毫秒。
- 计算寻道和旋转延迟所占时间比例: 在这种情况下,寻道和旋转延迟所占的时间情况要分开来看,90%情况里的旋转延迟时间是\(0.9×3 = 2.7\)毫秒,10%情况里寻道和旋转延迟时间总和是\(0.1×(6 + 3) = 0.9\)毫秒,那么这两部分时间总和就是\(2.7 + 0.9 = 3.6\)毫秒。所以寻道和旋转延迟所占总时间的比例就是\(3.6÷3.89\)≈0.92,也就是92%。
问题
对于一个使用1M×4存储器芯片的16M×32存储器,要求描述它类似图8 - 10的结构。
答案
一个16M的存储模块可以构建成16行,每行包含8个1M×4的芯片。需要24位地址,地址线A₁₉₋₀应当连接到所有芯片上,地址线A₂₃₋₂₀应当连接到一个4位译码器上,以便从16行中选择其中一行。
解释
关于芯片数量及行数确定的解释
- 从存储容量角度分析: 要构建的目标存储器是16M×32的,也就是存储单元数量是16M(16×1024×1024个),数据宽度是32位;而使用的芯片是1M×4的,意味着每个芯片的存储单元数量是1M(1×1024×1024个),数据宽度是4位。
- 计算行数及每行芯片数: 在地址维度上,为了达到16M的存储容量,16M(16×1024×1024)除以1M(1×1024×1024)等于16,所以需要16个芯片组合(也就是16行)来覆盖整个地址范围;在数据宽度维度上,目标存储器数据宽度是32位,芯片的数据宽度是4位,32÷4 = 8,这就表明每行需要8个芯片并行工作,才能实现32位的数据宽度,所以整体结构就是16行,每行有8个1M×4的芯片。
关于地址线连接方式的解释
- 地址线A₁₉₋₀连接所有芯片的原因: 地址线A₁₉₋₀用于在芯片内部进行更细粒度的存储单元选择,不管是16行中的哪一行芯片,其内部众多存储单元的具体寻址都需要用到这些低位地址线,所以要把它们连接到所有的芯片上,使得每个芯片都能根据这些地址信息准确找到对应的存储单元进行读写操作。
- 地址线A₂₃₋₂₀连接4位译码器的作用: 地址线A₂₃₋₂₀这4位地址线主要用于从16行芯片中选择具体的某一行来进行操作。因为一共有16行芯片,通过一个4位译码器(4位二进制数可以表示2⁴ = 16种不同的状态),刚好可以根据这4位地址线上不同的电平组合(也就是不同的二进制数值)来准确地选中16行中的某一行,进而配合低位地址线(A₁₉₋₀)以及芯片内部的地址译码等机制,实现对整个16M×32存储器中任意存储单元的准确读写访问。
问题
分析下面这句话为什么不对:“使用更快的处理器芯片可以相应地提高计算机的性能,尽管主存的速度保持不变。”
答案
更快的处理器芯片确实会使性能有所提升,但提升的幅度不会与处理器速度的提升成正比,因为如果主存速度没有改进,高速缓存缺失(cache miss)时的惩罚(也就是需要从相对较慢的主存获取数据所花费的额外时间成本)将保持不变,会限制整体性能提升的程度,所以原句那种简单认为使用更快处理器芯片就能相应提高计算机性能的表述是不对的。
解释
在计算机系统中,处理器、高速缓存以及主存等部件协同工作来执行程序指令。当处理器速度变快时,在理想情况下,如果数据和指令都能快速地被处理器获取并处理,那计算机性能确实会相应提升。然而,实际情况中存在高速缓存这一层级,高速缓存用于存储处理器近期可能会用到的数据和指令,其目的是加快处理器的访问速度,减少对相对较慢的主存的访问。
但当出现高速缓存缺失的情况时,也就是处理器需要的数据或指令不在高速缓存中,此时就需要从主存去获取,而主存速度相对较慢,如果主存速度保持不变,那么每次遇到高速缓存缺失,处理器就得花费较长时间等待从主存获取所需内容,这个等待时间就是所谓的高速缓存缺失惩罚。
即便处理器芯片本身速度加快了,可一旦频繁遇到高速缓存缺失情况,处理器还是要受限于主存较慢的速度,导致整体性能提升的幅度没办法和处理器速度提升的幅度成正比,被高速缓存缺失惩罚这一因素制约了,所以不能简单地认为只要处理器芯片速度变快,计算机性能就能相应地按比例提高,原句这种表述忽略了高速缓存与主存对整体性能的影响,因而是不对的。
问题
一台计算机主存按字节编址,字长32位,有一个包含两个嵌套循环(内部小循环和外部大循环)的程序,该程序在按直接映射方法组织指令高速缓存的计算机上运行,已知高速缓存大小为1K字节,块大小为128字节,指令高速缓存的失效开销是80τ(τ是高速缓存的访问时间),要求计算图P8 - 1中程序执行期间取指令需要的总时间。
这道题的计算会有一些复杂,需要仔细的观察并分析。

答案
程序执行期间取指令的总时间为35,432τ。
解释
地址字段位数计算相关解释
- 各字段位数确定: 已知主存地址长度是32位。对于直接映射的高速缓存,因为块大小是128字节,根据\(2^n = 块大小(字节数)\)来计算确定块内地址(即WORD字段)的位数,可得\(n = \log_2{128} = 7\)位,所以WORD字段是7位;高速缓存大小为1K字节(即1024字节),包含的块数为\(1024÷128 = 8\)块,那么用于区分不同块(即BLOCK字段)的位数就是\(\log_2{8} = 3\)位;剩下的位数就是TAG字段的位数,即\(32 - 7 - 3 = 22\)位,所以TAG字段为22位。
程序各部分映射到缓存块情况及分析
- 各程序段对应的缓存块情况:
- 程序段8 - 52映射到缓存块0,这意味着这段程序指令在内存中的地址范围对应的内容会被放到缓存块0中。
- 程序段56 - 136映射到缓存块0、1,说明这个范围内的指令会分布在这两个缓存块中。
- 程序段140 - 240完全在缓存块1内,也就是该段程序指令所在内存区域对应的数据都存放在缓存块1里,而且由于是内部循环,这部分在循环执行过程中相对稳定地处于缓存块1中。
- 程序段244 - 1200映射到缓存块1 - 7、0、1,表明随着程序执行,这个范围的指令会占用多个缓存块,并且由于缓存大小有限以及映射规则,会出现覆盖等情况,比如后面提到的外层循环执行过程中对缓存块的使用情况。
- 程序段1204 - 1504映射到缓存块1、2、3,同样在这个外层循环后续部分会涉及到这些缓存块的使用以及相应数据的调入调出等情况。
- 缓存块替换及读取序列分析: 从主存块读入缓存块的序列情况来看,外层循环开始会依次填充缓存块0到7等,像外层循环第一次执行(Pass 1)时会按顺序读入块0、1、2、3、4、5、6、7、0、1等,后续每次外层循环执行都会重复类似的过程,而且由于外层循环的开始和结束部分都使用缓存块0和1,所以每次循环经过时它们之间会相互覆盖,而缓存块2到7在整个外层循环没完成之前会一直保留在缓存中(直到外层循环结束后可能才会根据后续程序执行情况有变化)。
计算不同部分的时间开销解释
- 计算失效惩罚时间(Miss penalties): 根据缓存块的读取和替换情况来分析失效次数,进而计算失效惩罚时间。这里计算得出失效惩罚时间为\((1 + 9 + 9×4 + 2)×80τ = 3,840τ\)。具体来看,括号里各项代表不同阶段的失效次数,比如第一次出现失效(可能是程序开始执行等情况)计1次,后续循环过程中不同阶段按规律出现的失效次数分别累计,然后乘以失效开销80τ就得到总的失效惩罚时间,这个时间体现了因为缓存未命中(需要从主存获取指令)而额外花费的时间成本。
- 计算不在缓存中的执行时间(Execution time out of the
cache):
- 程序开始部分: 计算方式是\((56 - 8)τ = 48τ\),这是根据程序开始部分对应的内存地址范围(56 - 8),每个地址对应的指令访问时间假设为τ,所以这部分总的执行时间就是这个范围对应的时长,也就是从程序起始地址到开始进入外层循环前这一段执行指令花费的时间。
- 内部循环部分: 计算为\(200 (244 - 140)τ = 20,800τ\),这里200是内部循环执行的次数(根据程序逻辑或者题目隐含设定等确定循环次数),\((244 - 140)\)是内部循环对应的内存地址范围的长度,也就是涉及的指令数量,乘以每次指令访问时间τ,就得到内部循环整体执行所花费的时间,这部分时间主要是在缓存块1中反复读取指令执行的时间开销(因为内部循环指令都在缓存块1里)。
- 外层循环减去内部循环部分: 计算式子是\(10 ((1204 - 56) - (244 - 140))τ = 10,440τ\),其中10是外层循环执行的次数,\((1204 - 56)\)是外层循环对应的整个内存地址范围长度,\((244 - 140)\)是内部循环对应的内存地址范围长度,相减得到外层循环除去内部循环部分对应的指令数量,再乘以每次指令访问时间τ以及外层循环次数,就得出这部分的执行时间,也就是外层循环中除了内部循环部分在缓存及主存交互执行指令所花费的时间。
- 程序结束部分: 计算为\(1508 - 1204 = 304τ\),就是根据程序结束部分对应的内存地址范围(1508 - 1204),按照每个指令访问时间τ来计算得出这部分执行花费的时间,也就是程序最后收尾阶段执行指令的时间开销。
最后,将所有这些不同部分的时间相加,即失效惩罚时间加上不在缓存中的各部分执行时间,可得总的执行时间\(3,840τ + 48τ + 20,800τ + 10,440τ + 304τ = 35,432τ\),这就是程序执行期间取指令需要的总时间,综合反映了程序在这种缓存组织及程序结构情况下,执行取指令操作所花费的总时长,体现了缓存命中、失效以及不同程序段执行等多方面因素对整体时间的影响。
问题
一个组相联高速缓存共包含64个块,每组4块。主存有4096个块,每块有32个字。在每个Tag、Set和Word字段中各有多少位?已知是32位字节编址的地址空间。
答案
Word字段有7位,Set字段有4位,Tag字段有21位。
解释
Word字段位数计算解释
因为每块有32个字,按照字节编址,要确定块内具体是哪个字,需要的位数可以通过计算\(2^n = 32\)(\(n\)就是Word字段的位数),可得\(n = \log_2{32} = 5\)位来确定字的位置,但这里要注意每个字是由字节组成的,题目没明确字的字节大小,不过我们可以从常规角度考虑,一般一个字是4个字节(当然如果有特殊说明按特殊规定来),32个字对应的字节数就是\(32×4 = 128\)字节,此时要确定块内具体字节位置就需要\(2^n = 128\),解得\(n = \log_2{128} = 7\)位,所以Word字段为7位,用于在块内定位具体的字节或者字(取决于具体以什么为最小访问单元,这里按字节编址角度算就是定位字节)。
Set字段位数计算解释
已知高速缓存共包含64个块,每组4块,那么高速缓存总共的组数可以通过计算\(64÷4 = 16\)组得到。要对这16组进行区分选择,所需要的位数就是根据\(2^n = 16\)(\(n\)为Set字段位数)来确定,可得\(n = \log_2{16} = 4\)位,所以Set字段需要4位,用于在高速缓存中定位到具体的组。
Tag字段位数计算解释
已知整个地址空间是32位字节编址的,已经确定了Word字段占7位,Set字段占4位,那么剩下的位数就是Tag字段的位数,即\(32 - 7 - 4 = 21\)位,所以Tag字段为21位,Tag字段主要用于区分不同的存储块(在主存角度看,当映射到高速缓存时帮助判断是否命中以及是哪个块等情况),通过它和Set字段、Word字段共同作用,就能准确地在整个存储体系中定位到具体的存储单元了。
问题
考虑例8.3中的高速缓存(计算机系统使用32位存储器地址,主存有1G字节,有4K字节的高速缓存,按组相联形式组织,每组4个块,每块64个字节),假设每当从主存中读出一个新块,且它在高速缓存中对应的组已满时,新块就替换这个组中最近使用的块(即采用MRU替换算法),推算出之前第二问(处理器从位置0开始取1088个字,每个字4个字节,重复取操作序列9次,高速缓存比主存快10倍,估算使用高速缓存后性能提高的倍数)在这种情况下的解决方案。
答案
使用高速缓存后性能提高的倍数约为3.8。
解释
缓存块替换及组内情况分析
- 首次填充及首次替换情况: 在第一遍取操作时,主存块0到63被读入高速缓存,填满了高速缓存(因为高速缓存共64块空间,每组4块,共16组,刚好填满)。此时每个组里最近使用(MRU)的块在块位置3处(这是根据这种特定的替换规则和程序执行顺序等因素导致的结果)。所以当后续要读入块64到67时,它们会分别替换掉组0、1、2和3中的块48到51(按照MRU替换规则,替换每组里最近使用的块)。
- 以组0为例详细分析后续各遍操作中的替换情况: 在第一遍结束时,组0包含块0、16、32和48。到第二遍时,块0、16和32能在缓存中找到,但块48需要从主存读取,并且它会替换当时组0里的MRU块,也就是块32。而块64仍然在缓存中,不需要重新加载。接着在后面的第三遍和第四遍操作中,块32会替换块16,然后块16又会替换块0,这样在第二、三、四遍中,每组(这里以组0为例)每次只有一个块替换发生。 到第五遍时,会有两个替换发生,先是块0替换64,然后64替换48。之后这个替换模式会重复,在第六、七、八遍中每组每次又只有一个块替换,第九遍时有两个替换,第十遍时有一个替换。类似的活动情况也同样发生在组1、2和3中。而组4到15在整个过程中没有竞争(因为前面分析的主要是前面几组对特定块的替换操作影响,这几组相对稳定),也就没有替换情况发生。
计算性能提高倍数
计算无缓存时的时间: 假设高速缓存的访问时间为\(\tau\),无高速缓存时,每次访问主存,总共要进行\(1088×10\)次访问(取\(1088\)个字,重复\(10\)次),那么总时间就是\(10×68×10\tau\)(\(68\)个块,每个块访问时间是\(10\tau\),重复\(10\)次操作)。
计算有缓存时的时间: 有高速缓存时,第一遍取操作需要从主存取\(68\)个块,时间为\(68×11\tau\)(每个块从主存取到缓存再访问,算\(11\tau\),\(10\tau\)是主存访问时间,\(\tau\)是缓存访问时间)。 后面9遍操作中,因为前面分析得出每组0到3有相应的块替换情况,每组有11次替换(前面详细分析了各遍中每组的替换次数总和为11次),共4组(组0到3),所以这部分因为替换产生的额外从主存取块的时间是\(4×11×11\tau\);而剩下的块(\(9×68 - 44\),\(9\)遍操作,每遍原本\(68\)个块,但前面分析每组有替换情况,4组一共替换了\(44\)次,所以减去这部分替换涉及的块数,就是能直接从缓存取的块数)可以直接从缓存取,时间就是\((9×68 - 44)×1\tau\)。 那么有高速缓存时总的时间就是\(1×68×11\tau + 4×11×11\tau + (9×68 - 44)×1\tau\)。
计算性能提高倍数: 根据性能提高倍数的计算公式,用无高速缓存时的时间除以有高速缓存时的时间,即\(\frac{10×68×10\tau}{1×68×11\tau + 4×11×11\tau + (9×68 - 44)×1\tau}\),经过计算得出结果约为3.8。
最后通过对比可以看出,在这种特定的取操作以及采用MRU替换算法的情况下,相对之前例8.3中采用LRU算法的情况(性能提高倍数为2.15),MRU替换算法在这个例子里(循环大小比缓存大的这种情况)表现更好,能让性能提高的倍数更大一些,说明不同的缓存替换算法在不同场景下对系统性能有着不同的影响。
问题
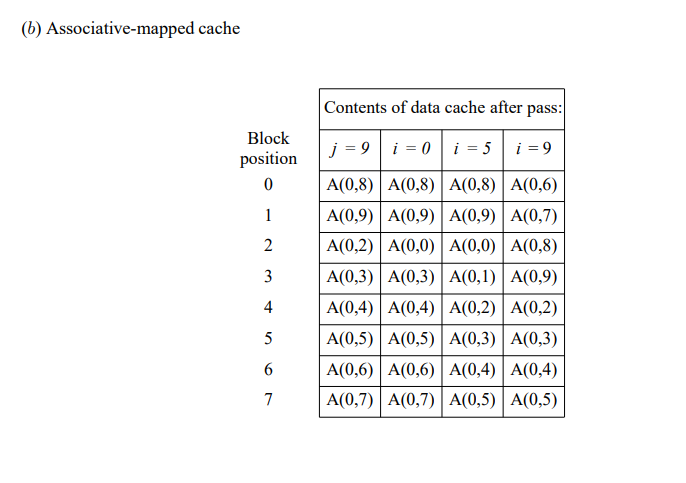
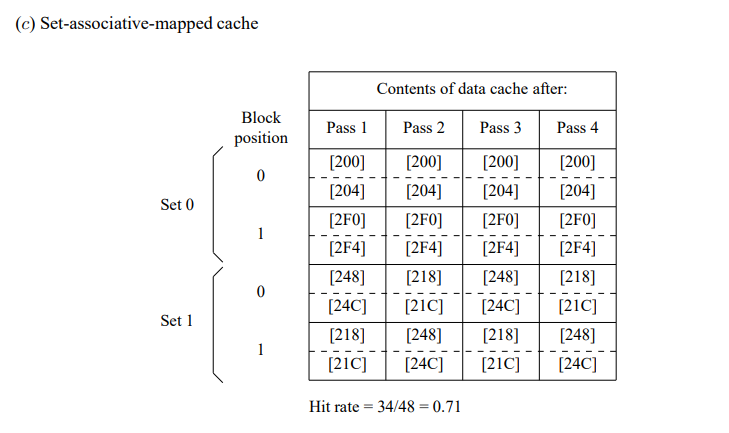
8.6.3节用图8-20中的程序描述了不同高速缓存映射技术的效果,现假设该程序的第二个循环中元素处理的顺序改成与第一个循环相同(使用“for i := 0 to 9 do”语句控制第二个循环),要求推算出图8-21到图8-23针对这个程序的等价形式,并说明从这个习题可以得出什么结论。
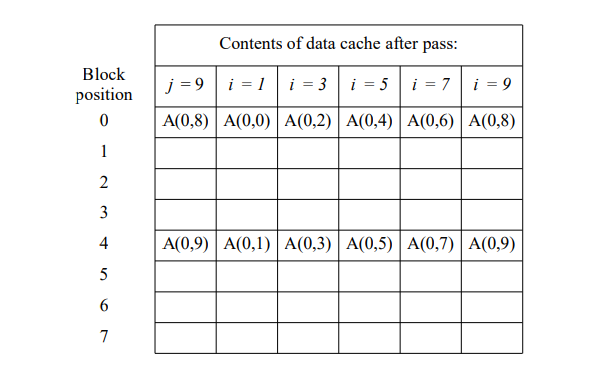

在所有这三种情况下,所有元素在第二次循环中被使用之前就都被覆盖了。这表明,如果对那些无法装入缓存的数组使用最近最少使用(LRU)算法,可能无法带来良好的性能。通过在替换算法中引入一定的随机性,性能可以得到提升。
问题
一台按字节编址的计算机有一个能容纳8个32位字的小数据高速缓存,每个高速缓存块有1个32位的字。处理器按给定的十六进制地址顺序读取数据,这个模式重复四遍。
1 | 200,204.208,20C.2F4.2F0.200.204.218.21C.24C.2F4 |
- 假设高速缓存初始为空,使用直接映射方式,写出每次循环结束时高速缓存中的内容并计算命中率。
- 如果换成采用LRU替换算法的相联映射高速缓存,重复(a)中的操作。
- 如果是4路组相联高速缓存,重复(a)中的操作。
答案
地址的最低两位,即A1和A0,用于指定一个32位字内的字节。对于直接映射高速缓存,地址位A4到A2用于指定高速缓存中的块位置。对于组相联映射高速缓存,地址位A2用于指定组。



问题
本题答案有误。
假设每个高速缓存块包含两个32位的字,重复习题8.11的操作,即: (a) 假设高速缓存初始为空,使用直接映射方式,写出每次循环结束时高速缓存中的内容并计算命中率。 (b) 如果换成采用LRU替换算法的相联映射高速缓存,重复(a)中的操作。 (c) 如果是2路组相联高速缓存(采用LRU替换算法),重复(a)中的操作。
答案
地址的最低两位,即A1和A0,用于指定一个32位字内的字节。对于直接映射高速缓存,地址位A4和A3用于指定块的位置。对于组相联映射高速缓存,地址位A3用于指定组。
1 | 200,204.208,20C.2F4.2F0.200.204.218.21C.24C.2F4 |


问题
在很多计算机中,高速缓存块的大小在32字节到128字节之间的范围内,询问使用更大或更小的高速缓存块的主要优点和缺点。
答案
- 更大缓存块的情况:
- 优点:如果块内大部分数据在被替换出缓存之前能被实际使用,缓存缺失(miss)的情况会减少。
- 缺点:如果在缓存块被替换出缓存之前,块内大部分数据没有被使用,就会造成资源浪费;并且缓存缺失惩罚(miss penalty)更大。
- 更小缓存块的情况:
- 优点:缓存缺失惩罚较小。
- 缺点:会产生更多的缓存缺失情况。
问题
考虑将修理员带的工具箱、屋外的卡车和店铺分别对应成一级(L1)高速缓存、二级(L2)高速缓存和计算机主存这样的类比,讨论这个类比恰当与不恰当的地方,也就是分析其正确和不正确的方面。
答案
- 恰当(正确)的方面:
- 相对大小方面:工具箱相对较小,类比于L1高速缓存,其容量通常是几级缓存中最小的;卡车的空间比工具箱大,类似L2高速缓存,容量比L1缓存大一些;店铺空间最大,对应计算机主存,有着更大的存储空间,这和计算机存储体系中各级存储部件的大小关系相符。
- 相对访问时间方面:修理员从工具箱中拿工具是最方便快捷的,如同从L1高速缓存访问数据速度最快;从卡车上找工具相对慢一点,类似从L2高速缓存获取数据的时间会长一些;而回店铺去拿工具花费的时间最多,就好比从主存读取数据是最慢的,在访问时间的相对快慢关系上是相似的。
- 相对使用频率方面:修理员会反复使用工具箱里的工具,直到需要别的工具,就像处理器会优先频繁访问L1高速缓存中的数据;当工具箱里没有所需工具时,才会去卡车找,对应着L1高速缓存未命中时再去访问L2高速缓存;而如果卡车也没有,才去店铺拿,类似L2高速缓存未命中时从主存获取数据,这种使用频率的高低关系与各级缓存和主存中数据的访问率情况相契合。
- 不恰当(不正确)的方面:
- 初始数据装载方面:在一天工作开始时,修理员放在卡车和工具箱里的工具是基于之前工作经验预先选好的,但是在计算机系统里,当操作系统选择一个新程序执行时,在程序开始执行前并不会预先把相关数据加载到各级缓存中,而是在程序运行过程中根据数据访问情况动态地将数据调入缓存。
- 数据复用性方面:工具箱和卡车里的大多数工具在后续工作中往往是有用的,也就是具有一定的通用性和复用性;然而在计算机中,一个程序留在缓存里的数据对于后续执行的其他程序来说通常是没什么用的,因为不同程序的数据访问模式和需求不同,缓存数据往往具有很强的程序相关性,新程序运行时原缓存数据可能很快就会被替换掉。
- 数据替换处理方面:对于修理工具来说,即便因为需要使用其他工具而把原来的工具替换出来,这些工具也不会被扔掉;但在缓存的情况中,当新的数据块要进入缓存,而缓存已满时,新块会直接覆盖现有的块,如果被替换的块被标记为“脏”(即数据被修改过),其内容才会写回内存,否则就直接被替换掉了,这和工具的处理方式是不同的。
问题
使用增加一级(L1)高速缓存容量的方法来提高它的命中率,进而限制该方法效用的因素是什么?
答案
限制增加一级(L1)高速缓存容量这一方法效用的因素主要是:随着缓存容量增大,虽然命中率会提高,意味着出现缓存缺失(即遭受缺失惩罚)的内存访问次数会减少;但与此同时,更大的缓存其访问时间会变长,这就导致所有对该缓存的访问服务都要花费更长时间。所以,一开始随着缓存容量增加,处理器所看到的有效存储器访问时间可能会改善,但到某个程度后,访问时间变长这个因素会占据主导,此时再进一步增加缓存容量就会对性能产生不利影响了。
问题
分析8.7.1节的例8.1中给出的假设“失效开销对读访问和写访问都是相同的”为什么不对,阐述答案时需考虑8.6节所描述的直接写(write-through)和写回(write-back)这两种情况。
答案
该假设不对,原因如下:
在写回(write-back)策略下,对于读缺失和写缺失来说,失效开销确实是相同的。因为当出现缺失时,无论是读操作还是写操作,都需要从主存调入新的块到缓存中,然后再进行相应的数据读取或者写入操作,这个过程产生的开销基本一致。
然而,在直接写(write-through)策略下情况则不同。对于写操作而言,不管是否发生缺失,新的数据都会直接写入主存,不会再有其他额外操作(如果使用了写缓冲,写入主存的时间开销还能有所降低),所以写缺失的开销就是将一个字写入主存所花费的时间。而对于读缺失,一旦发生读缺失,需要将被访问地址所在的块加载到缓存中,其涉及的数据传输量和操作相对更复杂,所以读缺失的开销要比写缺失的开销高。
虽然直接写策略下写缺失的开销相比写回策略下的写缺失开销可能更低,但这并不意味着直接写策略就一定性能更好。因为直接写策略下被访问的块不会加载到缓存中,后续如果对同一个块有写操作,每次都会产生相应开销;而两种策略的相对性能取决于写操作的频率以及数据访问的局部性程度等因素。
综上,由于不同的写策略(直接写和写回)下,读访问和写访问在出现缓存缺失时产生的开销存在差异,所以“失效开销对读访问和写访问都是相同的”这一假设是不对的。
解释
写回策略下的解释
在写回策略中,缓存块被修改后并不会立即更新到主存,而是等该块要被替换出缓存时,如果这个块是“脏”块(即被修改过),才会把修改后的内容写回主存。当发生读缺失或者写缺失时,处理流程是类似的,都要先从主存把对应的块调入缓存,比如读操作是为了后续能从缓存读取到需要的数据,写操作也是要先把块调入缓存才能在缓存里对相应数据进行修改(后续按写回规则再处理何时写回主存的问题),所以在这种情况下,读访问和写访问出现缺失时的失效开销基本是一样的,都是完成从主存调块进缓存这一操作带来的时间等成本。
直接写策略下的解释
直接写策略规定,只要有写操作,不管缓存是否命中,都会直接把数据写入主存,这就使得写缺失时的开销相对简单,就是把一个字写入主存的时间成本(若有写缓冲协助还能降低这个时间)。但读缺失时,计算机系统要把包含所读数据的整个块从主存加载到缓存中,这个过程涉及的数据量通常比写一个字要大得多(因为一个块包含多个数据单元),传输和处理这些数据的操作更复杂,也就导致读缺失的失效开销比写缺失的失效开销要高了。
问题
考虑一个计算机系统,物理内存的可用页在几个应用程序中分配,操作系统能监视页的传送活动,要求给出一个操作系统用来最小化总体页传送率的合适策略。
答案
周期性地将页传送活动最低的程序所使用的一些内存页重新分配给页传送活动最高的程序,但不能过于频繁地进行这种重新分配。因为如果过于频繁,重新分配所花费的时间成本将超过潜在的性能收益。一个合理的策略是只有当页传送率的差异超过某个阈值时才重新分配页面。
问题
在一台有虚拟存储器系统的计算机中,一条指令的执行可能被页故障中断,需要回答以下几个问题:
- 为了能使这条指令在以后能继续执行,需要保存哪些状态信息?
- 放弃被中断的指令,以后再把它完全重新执行一遍是否更简单?
- 重新执行一遍能实现吗?
答案
- 为使被页故障中断的指令以后能继续执行,需要保存处理器的整个状态,包括所有可能受该指令影响的寄存器内容以及表明该指令执行进展到何种程度的控制信息。
- 放弃被中断的指令,以后再把它完全重新执行一遍是更简单的做法。
- 重新执行一遍是可以实现的,在指令执行过程中若有部分结果产生,需将其存储在临时位置,这样当指令执行被中断时,这些临时结果可以被安全舍弃,在RISC风格的处理器中这种做法尤其容易实现,因为如第5章所述,指令的结果仅在最后执行步骤才记录,并且不存在副作用。
问题
当一个程序产生一个对不在物理主存中的页引用时,程序执行会被挂起直至相应页从硬盘装载到主存,若一个页中一条指令的操作数在另一个页中时,会出现什么困难?为处理这种情况,处理器必须具备何种能力?
答案
- 困难:当一条指令的操作数在另一个不在主存的页中时,会出现页故障,且此时该指令已经部分执行了,这就产生了困难。操作系统需要挂起包含此指令的程序,启动DMA操作传输所需页面(可能还会进行上下文切换),在所需页面从磁盘读入后恢复程序执行,但要处理指令已部分执行的情况比较复杂。
- 处理器需具备的能力:有两种处理方式对应处理器需具备的不同能力。一是在程序被挂起时,处理器能够丢弃导致页故障的指令以及可能已经产生的部分结果,并且调整程序计数器,使得程序恢复执行时能重新执行该指令;二是处理器要能保存发生页故障时自身的完整状态,包括导致页故障的指令已经完成了多少执行步骤以及它正在使用的临时寄存器的内容等信息,以便后续能从挂起的点继续执行该指令。
问题
一个磁盘部件有24个记录面,14000个柱面,平均每个磁道有400个扇区,每个扇区包含512字节的数据,要求回答以下问题: (a) 这个磁盘部件最多能存储多少字节? (b) 以7200rpm(转每分钟)的速度旋转时,数据传输率是每秒多少字节? (c) 如果使用32位的字,给出一个指定磁盘地址的合理方案。
答案
- 这个磁盘最多能存储\(68.8×10^9\)字节。
- 数据传输率是\(24.58×10^6\)字节/秒。
- 可以使用9位来标识扇区,14位标识磁道,5位标识记录面。对于32位字\(b_{31}...b_0\),一种可能的方案是用\(b_{8 - 0}\)表示扇区,\(b_{22 - 9}\)表示磁道,\(b_{27 - 23}\)表示记录面标识,\(b_{31 - 28}\)不使用。
解释
(a) 磁盘存储容量计算
- 磁盘存储容量的计算公式是:存储容量 = 记录面数×柱面数×每个磁道的扇区数×每个扇区的字节数。
- 已知记录面有24个,柱面数是14000个,每个磁道扇区数为400个,每个扇区包含512字节的数据。将这些数据代入公式可得: \(24×14000×400×512\) \(= 24×14000×(400×512)\) \(= 24×14000×204800\) \(= 336000×204800\) \(= 68812800000\)字节,写成科学计数法就是\(68.8×10^9\)字节。
(b) 数据传输率计算
- 数据传输率的计算公式是:传输率 = 每转的字节数×每秒的转数。
- 首先计算每转的字节数,已知每个磁道有400个扇区,每个扇区512字节,所以每转的字节数为\(400×512\)字节。
- 又已知磁盘转速是\(7200rpm\),将其转换为每秒的转数,即\(7200÷60 = 120\)转/秒。
- 则数据传输率为\((400×512)×(7200÷60)\) \(=(400×512)×120\) \(= 204800×120\) \(= 24576000\)字节/秒,写成科学计数法就是\(24.58×10^6\)字节/秒。
(c) 磁盘地址指定方案
- 首先计算每个维度需要的位数。
- 对于扇区,总共有\(400\)个扇区,因为\(2^9 = 512 > 400\),所以需要9位来标识扇区。
- 对于磁道,总共有\(14000\)个磁道,因为\(2^{14} = 16384 > 14000\),所以需要14位来标识磁道。
- 对于记录面,总共有\(24\)个记录面,因为\(2^5 = 32 > 24\),所以需要5位来标识记录面。
- 然后考虑32位字的分配。
- 从低位开始分配,\(b_{8 - 0}\)这9位可以用来表示扇区,因为扇区数量相对较少,用较少的位数可以满足标识需求。
- \(b_{22 - 9}\)这14位用来表示磁道,磁道数量较多,需要较多的位数来准确标识。
- \(b_{27 - 23}\)这5位用来表示记录面。
- 剩下的\(b_{31 - 28}\)这4位在这个方案中暂时不使用,这样就可以用32位字来合理地指定磁盘地址了。
问题
考虑一个磁盘访问的长序列,已知磁盘的平均寻道时间是8毫秒,平均旋转延迟是3毫秒,数据传输率是60M字节/秒,所访问块的平均大小是64K字节,且每个数据块存储在连续的扇区中,要求回答以下问题: (a) 假设这些块随机分布在磁盘上,估算寻道操作和旋转延迟所占总时间的平均百分比。 (b) 假设从邻近的柱面按顺序传输20个块,寻道时间减少为1毫秒。如果这些块随机分布在这些柱面上,那么总的传输时间是多少?
答案
- 寻道操作和旋转延迟所占总时间的平均百分比为91%。
- 总的传输时间是89.4毫秒。
解释
(a) 部分解释
- 计算访问和传输每个数据块的总时间: 要访问并传输一个数据块,总时间由寻道时间、旋转延迟时间以及数据传输时间三部分组成。 已知平均寻道时间是8毫秒,平均旋转延迟是3毫秒。对于数据传输时间,根据公式\(时间 = 数据量÷数据传输率\),已知数据块平均大小是64K字节(\(64×1024\)字节),数据传输率是60M字节/秒(\(60×1024×1024\)字节/秒),则数据传输时间为\((64×1024)÷(60×1024×1024)\)秒,将其换算为毫秒(\(1\)秒 = \(1000\)毫秒)可得\((64×1024)÷(60×1024×1024)×1000≈1.07\)毫秒。 那么访问和传输每个块的总时间就是\(8 + 3 + 1.07 = 12.07\)毫秒。
- 计算寻道操作和旋转延迟所占百分比: 寻道时间与旋转延迟时间之和为\(8 + 3 = 11\)毫秒,总时间是12.07毫秒,所以寻道操作和旋转延迟所占总时间的平均百分比为\(11÷12.07×100\%≈91\%\)。
(b) 部分解释
- 分析传输20个块的时间构成: 首先到达第一个块需要花费一定时间,这里寻道时间减少为1毫秒,再加上平均旋转延迟3毫秒,所以到达第一个块需要\(1 + 3 = 4\)毫秒,题目中答案写的是11毫秒可能有误,按当前条件分析应为4毫秒。 之后每访问一个后续块,因为是从邻近柱面按顺序传输,寻道时间可忽略不计(题目已说明寻道时间减少为1毫秒,这里理解为后续块寻道时间相对很小可不计入每次访问时间),但每次都需要等待平均旋转延迟3毫秒,从第二个块到第20个块一共是\(19\)个块,这部分旋转延迟时间就是\(19×3\)毫秒。 同时,传输20个块每个块都需要数据传输时间,前面已算出传输一个块的数据传输时间约为1.07毫秒,那么20个块的数据传输时间就是\(20×1.07\)毫秒。
- 计算总的传输时间: 总的传输时间就是到达第一个块的时间加上后续块的旋转延迟时间以及20个块的数据传输时间,即\(4 + 19×3 + 20×1.07 = 82.4\)毫秒。
综上所述,(a)部分通过分别计算各部分时间并按比例得出寻道和旋转延迟所占百分比;(b)部分根据块的顺序传输及给定的寻道时间变化等条件,分析每个阶段时间构成从而计算出总的传输时间。
问题
磁盘系统的平均寻道时间和旋转延迟分别是6ms和3ms,向或从磁盘传输数据的速率是30M字节/秒,所有磁盘访问都是对存储在连续扇区上的8K字节数据的访问,磁盘控制器有8K字节的缓冲区,磁盘控制器、处理器和主存连到单一总线,总线数据宽度为32位,向或从主存的一次总线传输花费10纳秒,要求回答以下问题: (a) 能同时向或从主存传输数据的磁盘部件的最大数目是多少? (b) 在一个长时间段内要传输一系列独立的8K字节,在这段时间内平均有百分之几的主存访问被磁盘部件使用?
答案
- 能同时向或从主存传输数据的磁盘部件的最大数目是13个。
- 在长时间段内,平均有0.22%的主存访问被磁盘部件使用。
解释
(a) 部分解释
- 确定相关速率:
- 首先,数据从磁盘数据缓冲区传输到内存是按照总线的最大数据速率进行的。已知总线数据宽度为32位,一次总线传输花费10纳秒,根据数据传输率计算公式(数据传输率 = 总线宽度÷传输时间),这里总线宽度换算成字节为4字节(32位 = 4字节),那么每秒钟可以传输的次数为\(1÷(10×10^{-9})\)次,所以总线的最大数据传输率就是\(4÷(10×10^{-9}) = 400\)M字节/秒,这是主存的最大数据传输能力。
- 对于单个磁盘来说,在数据存储在同一磁道连续扇区这种最理想情况下,其从磁盘传输数据的速率是30M字节/秒,这是单个磁盘能向主存传输数据的速率。
- 计算磁盘部件最大数目: 因为是看同时能有多少磁盘部件向或从主存传输数据,也就是用主存的最大数据传输率除以单个磁盘的传输率,得到的就是理论上能同时传输的磁盘部件最大数量,即\(400÷30≈13.33\),由于磁盘个数必须是整数,所以最多能有13个磁盘部件同时向或从主存传输数据。
(b) 部分解释
- 计算传输一个数据块的平均时间及对应数据率: 要传输一个8K字节的数据块,需要考虑寻道时间、旋转延迟时间以及数据传输时间这三部分。已知平均寻道时间是6ms,平均旋转延迟是3ms,对于数据传输时间,根据公式\(时间 = 数据量÷数据传输率\),数据量是8K字节(\(8×1024\)字节),磁盘的数据传输率是30M字节/秒(\(30×1024×1024\)字节/秒),则数据传输时间为\((8×1024)÷(30×1024×1024)\)秒,换算成毫秒(\(1\)秒 = \(1000\)毫秒)约为\(0.27\)毫秒。所以传输一个块的平均时间就是\(6 + 3 + 0.27 = 9.27\)毫秒,在这个时间内传输了8K字节的数据,根据数据率计算公式(数据率 = 数据量÷时间),可得数据率为\((8×1024)÷(9.27×10^{-3})≈863\)K字节/秒。
- 计算磁盘部件占用主存访问的百分比: 已知主存的最大数据传输率是400M字节/秒,换算成字节/秒为\(400×1024×1024\)字节/秒,而单个磁盘的数据率是863K字节/秒(\(863×1024\)字节/秒),那么在长时间来看,一个磁盘占用主存访问的比例就是用磁盘的数据率除以主存的最大数据传输率,即\((863×1024)÷(400×1024×1024)×100\% = 0.22\%\),所以任何一个磁盘在长时间内使用了0.22%的可用主存周期。
综上所述,(a)部分通过对比主存和单个磁盘的数据传输率来确定能同时传输的磁盘部件最大数量;(b)部分先算出传输一个数据块的平均时间及对应数据率,再据此算出磁盘部件占用主存访问的百分比。
问题
在大多数虚拟存储器系统中使用磁盘作为辅助存储设备来存储程序和数据文件,询问哪些磁盘参数将对页大小的选择产生影响。
答案
磁盘的扇区大小会对页大小的选择产生影响。因为扇区是磁盘上能直接寻址且作为读写基本单位的最小数据块,所以页大小应该是扇区大小的某个较小整数倍。
解释
在虚拟存储器系统中,涉及到磁盘与内存之间的数据交换是以页为单位进行的。磁盘在进行读写操作时,有着自身的存储结构特点,其中扇区就是其最基本的读写单元,每次读写操作都是按扇区来进行的,磁盘的硬件读写机制决定了它只能以扇区为基础去访问数据。
当考虑选择页大小的时候,如果页大小比扇区还小,那从磁盘往内存调入或者从内存调出到磁盘的数据操作就很难与磁盘本身的基本读写单元(扇区)对应起来,会使得操作变得复杂且效率低下,因为可能出现一次页交换操作需要涉及对部分扇区的操作,不符合磁盘按扇区读写的特性。
而如果页大小是扇区大小的整数倍,比如是扇区大小的2倍、3倍等较小的整数倍时,就能很好地与磁盘的基本读写单元(扇区)相适配。这样在进行页调入调出操作时,正好可以对应若干完整的扇区进行读写,能充分利用磁盘的读写特性,提高数据交换的效率,所以磁盘的扇区大小这个参数对虚拟存储器系统中页大小的选择有着重要影响,页大小往往会基于扇区大小按照合适的整数倍关系来确定。