计组习题的那些事(7)
计组习题的那些事(7)
今天起床,感觉十分通透啊,是个不错的日子!!!
今天已经快过去了,确实,今天是个不错的日子,至少我收获颇丰。
问题:Booth算法

问题
将十进制小数 0.1 转换为二进制小数。若转换不精确,运用 9.7.2 节中讨论的三种截取方法(截断方法、冯·诺依曼舍入方法、舍入方法)将二进制小数近似为二进制小数点后 8 位。
答案
- 通过截断方法截取得到 0.00011001。
- 通过冯·诺依曼舍入方法截取得到 0.00011001。
- 通过舍入方法截取得到 0.00011010。
解释
按照 9.8 节给出的转换方法,把十进制小数 0.1 乘以 2,然后将所得乘积的小数部分再乘以 2,如此不断重复操作。每次乘积中,小数点左边的部分就生成相应的位序列,在这个例子里,生成的位序列是 0,0,0,1,1,0,0,1,1,0,0,1,1,… ,可以发现这个序列会无限循环下去,其重复模式为 0,0,1,1,这也就表明将十进制小数 0.1 转换为二进制小数是不精确的转换。
问题
考虑一种 12 位的浮点数表示格式,其中第 1 位是数的符号,接下来的 5 位表示比例因子(隐含的基数为 2)的余 15 格式的指数,最后 6 位表示尾数的小数部分,其二进制小数点的左边有一个隐含的 1。对于给定的操作数 A 和 B,A 表示为 1.011011×2⁰,对应的二进制表示为 10001 01111 011011;B 表示为 -1.101010×2⁰,对应的二进制表示为 101010 01111 101010。要求对操作数 A 和 B 执行减法和乘法操作,并给出相应结果。
答案



问题
- (a) 要求采用二级与或电路设计一个半加器,半加器有两个输入 \(x\) 与 \(y\),以及两个输出 \(s\)(\(x\) 与 \(y\) 相加所得的和)与 \(c\)(进位输出)。
- (b) 说明怎样使用两个半加器以及必要的外部逻辑门实现图 9-2a 中的全加器。
- (c) 比较 (b) 部分设计的网络和图 9-2a 中的加法器网络的最长逻辑延迟路径。
答案
- (a) 半加器实现如下(具体电路实现未给出详细内容,可能需结合相关逻辑电路知识进一步明确具体的与或门连接等情况)。
- (b) 未给出具体实现描述内容,无法确切知晓如何利用两个半加器及外部逻辑门实现全加器的详细步骤。
- (c) (b) 部分的电路在产生 \(s_i\) 时最长逻辑延迟路径是 4 个门延迟(不包括输入反相);而图 9-2a 中的加法器网络相关最长逻辑延迟路径情况未完整给出,无法直接对比两者具体差异,仅能知道 (b) 部分这一结果相关信息。
解释
(a) 部分解释
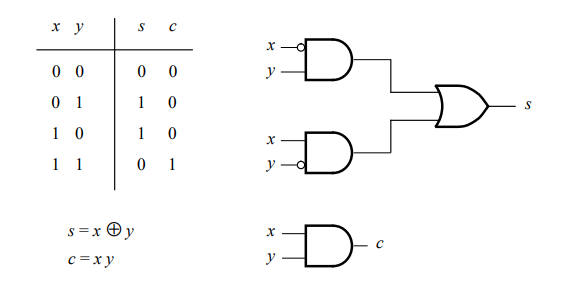

(c) 部分解释
在(b)部分的电路中,产生\(s_{i}\)的最长路径(不包括输入反相)有4个门延迟;而在图9.2a所示的电路中,假设\(s_{i}\)是以两级“与 - 或”电路来实现的,那么产生\(c_{i + 1}\)或者\(s_{i}\)的最长路径(不包括输入反相)有2个门延迟。
Booth

乘法


浮点数




本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Totoroの旅!
评论





