评价类模型

层次分析法

背景：

层次分析法作为一种主观权重设计方法，一般不需要大量的数据，适合应用于那些比较难以用定量方法解决的问题。

是在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上，利用较少的定量信息使决策的思维过程数学化，从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法

层次分析法的应用

img

Matlab 小知识

%% Matlab基本的小常识
% (1)在每一行的语句后面加上分号(一定要是英文的哦;中文的长这个样子；)表示不显示运行结果
a = 3;
a = 5

% (2)多行注释:选中要注释的若干语句,快捷键Ctrl+R
% a = 3;
% a = 5

% (3)取消注释:选中要取消注释的语句,快捷键Ctrl+T
% 我想要取消注释下面这行
% 还有这一行

% clear可以清楚工作区的所有变量
clear

% clc可以清除命令行窗口中的所有文本,让屏幕变得干净
clc

% 所以大家在很多代码开头，都会见到:
clear;clc   % 分号也用于区分行。
% 这两条一起使用，起到“初始化”的作用，防止之前的结果对新脚本文件（后缀名是 .m）产生干扰。

%% 输出和输入函数(disp 和 input)
% disp函数
% matlab中disp()就是屏幕输出函数，类似于c语言中的printf（）函数
disp('我是清风，大家好鸭~~~记得投币关注我哦')
a = [1,2,3]    %同一行中间用逗号分隔，也可以不用逗号，直接用空格
a = [1 2 3]
disp(a) 
% 注意，disp函数比较特殊，这里可要分号，可不要分号哦
disp(a);
% matlab中两个字符串的合并有两种方法
% （1）strcat(str1,str2……,strn) 
 strcat('字符串1','字符串2') 
% （2）[str 1,str 2，……, str n]或[str1  str2  ……  strn]
['字符串1'  '字符串2']
['字符串1','字符串2']
% 一个有用的字符串函数：num2str  将数字转换为字符串
c = 100
num2str(c)
disp(['c的取值为' num2str(c)])
disp(strcat('c的取值为', num2str(c)))

% input函数
% 一般我们会将输入的数、向量、矩阵、字符串等赋给一个变量，这里我们赋给A
A = input('请输入A：');
B = input('请输入B：')
% 注意观察工作区，并体会input后面加分号和不加分号的区别

%% sum函数
% （1）如果是向量（无论是行向量还是列向量），都是直接求和
E = [1,2,3]
sum(E)
E = [1;2;3]
sum(E)
% （2）如果是矩阵，则需要根据行和列的方向作区分
clc
E = [1,2;3,4;5,6]
% a=sum(x); %按列求和(得到一个行向量）
a = sum(E)
a = sum(E,1)
% a=sum(x,2); %按行求和(得到一个列向量）
a = sum(E,2)
% a=sum(x(:));%对整个矩阵求和
a = sum(sum(E))
a = sum(E(:))

%% 基础：matlab中如何提取矩阵中指定位置的元素？
% （1）取指定行和列的一个元素（输出的是一个值）
clc;A=[1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1];
A
A(2,1)
A(3,2)
% （2）取指定的某一行的全部元素（输出的是一个行向量）
clc;A
A(2,:)
A(5,:)
% （3）取指定的某一列的全部元素（输出的是一个列向量）
clc;A
A(:,1)
A(:,3)
% （4）取指定的某些行的全部元素（输出的是一个矩阵）
clc;A
A([2,5],:)      % 只取第二行和第五行（一共2行）
A(2:5,:)        % 取第二行到第五行（一共4行）
A(2:2:5,:)     % 取第二行和第四行 （从2开始，每次递增2个单位，到5结束）
1:3:10
10:-1:1
A(2:end,:)      % 取第二行到最后一行
A(2:end-1,:)    % 取第二行到倒数第二行
% （5）取全部元素(按列拼接的，最终输出的是一个列向量)
clc;A
A(:)

%% size函数
clc;
A = [1,2,3;4,5,6]
B = [1,2,3,4,5,6]
size(A)
size(B)
% size(A)函数是用来求矩阵A的大小的,它返回一个行向量，第一个元素是矩阵的行数，第二个元素是矩阵的列数
[r,c] = size(A)
% 将矩阵A的行数返回到第一个变量r，将矩阵的列数返回到第二个变量c
r = size(A,1)  %返回行数
c = size(A,2) %返回列数

%% repmat函数
% B = repmat(A,m,n):将矩阵A复制m×n块，即把A作为B的元素，B由m×n个A平铺而成。
A = [1,2,3;4,5,6]
B = repmat(A,2,1)
B = repmat(A,3,2)

%% Matlab中矩阵的运算
% MATLAB在矩阵的运算中，“*”号和“/”号代表矩阵之间的乘法与除法(A/B = A*inv(B))
A = [1,2;3,4]
B = [1,0;1,1]
A * B
inv(B)  % 求B的逆矩阵
B * inv(B)
A * inv(B)
A / B

% 两个形状相同的矩阵对应元素之间的乘除法需要使用“.*”和“./”
A = [1,2;3,4]
B = [1,0;1,1]
A .* B
A ./ B

% 每个元素同时和常数相乘或相除操作都可以使用
A = [1,2;3,4]
A * 2
A .* 2
A / 2 
A ./ 2

% 每个元素同时乘方时只能用 .^
A = [1,2;3,4]
A .^ 2
A ^ 2 
A * A

%% Matlab中求特征值和特征向量
% 在Matlab中，计算矩阵A的特征值和特征向量的函数是eig(A),其中最常用的两个用法：
A = [1 2 3 ;2 2 1;2 0 3]
% （1）E=eig(A)：求矩阵A的全部特征值，构成向量E。
E=eig(A)
% （2）[V,D]=eig(A)：求矩阵A的全部特征值，构成对角阵D，并求A的特征向量构成V的列向量。（V的每一列都是D中与之相同列的特征值的特征向量）
[V,D]=eig(A)

%% find函数的基本用法
% 下面例子来自博客：https://www.cnblogs.com/anzhiwu815/p/5907033.html 博客内有更加深入的探究
% find函数，它可以用来返回向量或者矩阵中不为0的元素的位置索引。
clc;X = [1 0 4 -3 0 0 0 8 6]
ind = find(X)
% 其有多种用法，比如返回前2个不为0的元素的位置：
ind = find(X,2)

%上面针对的是向量（一维），若X是一个矩阵（二维，有行和列），索引该如何返回呢？
clc;X = [1 -3 0;0 0 8;4 0 6]
ind = find(X)
% 这是因为在Matlab在存储矩阵时，是一列一列存储的，我们可以做一下验证：
X(4)
% 假如你需要按照行列的信息输出该怎么办呢？
[r,c] = find(X)
[r,c] = find(X,1) %只找第一个非0元素


%% 矩阵与常数的大小判断运算
% 共有三种运算符：大于> ;小于< ;等于 ==  （一个等号表示赋值；两个等号表示判断）
clc
X = [1 -3 0;0 0 8;4 0 6]
X > 0
X == 4

%% 判断语句
% Matlab的判断语句，if所在的行不需要冒号，语句的最后一定要以end结尾 ；中间的语句要注意缩进。
a = input('请输入考试分数:')
if a >= 85  
    disp('成绩优秀')
elseif a >= 60 
    disp('成绩合格')
else
    disp('成绩挂科')
end

A = [1,2,4;
    1/2,1,2;
    1/4,1/2,1]
[V,D] = eig(A)  % 求出A的特征值和特征向量
A*[1;1/2;1/4] - 3*[1;1/2;1/4]   % 验证[1;1/2;1/4]是否为特征值3对应的特征向量
% A X = /lamba X

第一步

建立层次结构模型 简述：

将决策的目标、考虑的因素(决策准则)和决策方案，按它们之间的相互关系分为最高层、中间层和最低层，绘出层次结构图。

最高层：决策的目的、要解决的问题。

中间层：考虑的因素、决策的准则。

最低层：决策时的备选方案。

对于相邻的两层，称高层为目标层，低层为因素层。

如图：

image-20240129161333080

image-20240129161346001

第二步

构造判断矩阵 从层次结构模型的第2层开始，对于从属于(或影响)上一层每个因素的同一层诸因素，构造判断矩阵，直到最下层。

在确定各层次各因素之间的权重时，如果只是定性的结果，则常常不容易被别人接受，因而Saaty等人提出：一致矩阵法，即：

1.不把所有因素放在一起比较，而是两两相互比较。

2.对此时采用相对尺度，以尽可能减少性质不同的诸因素相互比较的困难，以提高准确度。

判断矩阵是表示本层所有因素针对上一层某一个因素的相对重要性的比较。判断矩阵的元素���用Saaty的1-9标度方法给出。

心理学家认为成对比较的因素不宜超过9个，即每层不要超过9个因素。

image-20240129161357280

image-20240129161419855

image-20240129161445463

image-20240129161505143

第三步

计算单层权向量并做一致性检验

能否确认层次单排序，需要进行一致性检验，所谓一致性检验是指对A确定不一致的允许范围。

定理1：n阶一致阵的唯一非零特征根为n

定理2：n阶正互反阵A的最大特征根λ≥n，当且仅当λ=n时A为一致阵

image-20240129161525745

image-20240129161542137

image-20240129161552150

第四步

image-20240129161610809

局限性

image-20240129161633027

代码：

%% 注意：在论文写作中，应该先对判断矩阵进行一致性检验，然后再计算权重，因为只有判断矩阵通过了一致性检验，其权重才是有意义的。
%% 在下面的代码中，我们先计算了权重，然后再进行了一致性检验，这是为了顺应计算过程，事实上在逻辑上是说不过去的。
%% 因此大家自己写论文中如果用到了层次分析法，一定要先对判断矩阵进行一致性检验。
%% 而且要说明的是，只有非一致矩阵的判断矩阵才需要进行一致性检验。
%% 如果你的判断矩阵本身就是一个一致矩阵，那么就没有必要进行一致性检验。


%% 输入判断矩阵
clear;clc
disp('请输入判断矩阵A： ')
% A = input('判断矩阵A=')
A =[1 1 4 1/3 3;
 1 1 4 1/3 3;
 1/4 1/4 1 1/3 1/2;
 3 3 3 1 3;
 1/3 1/3 2 1/3 1]
% matlab矩阵有两种写法，可以直接写到一行:
% [1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]
% 也可以写成多行:
[1 1 4 1/3 3;
 1 1 4 1/3 3;
 1/4 1/4 1 1/3 1/2;
 3 3 3 1 3;
 1/3 1/3 2 1/3 1]
% 两行之间以分号结尾（最后一行的分号可加可不加），同行元素之间以空格（或者逗号）分开。

%% 方法1：算术平均法求权重
% 第一步：将判断矩阵按照列归一化（每一个元素除以其所在列的和）
Sum_A = sum(A)

[n,n] = size(A)  % 也可以写成n = size(A,1)
% 因为我们的判断矩阵A是一个方阵，所以这里的r和c相同，我们可以就用同一个字母n表示
SUM_A = repmat(Sum_A,n,1)   %repeat matrix的缩写
% 另外一种替代的方法如下：
    SUM_A = [];
    for i = 1:n   %循环哦，这一行后面不能加冒号（和Python不同），这里表示循环n次
        SUM_A = [SUM_A; Sum_A]
    end
clc;A
SUM_A
Stand_A = A ./ SUM_A
% 这里我们直接将两个矩阵对应的元素相除即可

% 第二步：将归一化的各列相加(按行求和)
sum(Stand_A,2)

% 第三步：将相加后得到的向量中每个元素除以n即可得到权重向量
disp('算术平均法求权重的结果为：');
disp(sum(Stand_A,2) / n)
% 首先对标准化后的矩阵按照行求和，得到一个列向量
% 然后再将这个列向量的每个元素同时除以n即可（注意这里也可以用./哦）

%% 方法2：几何平均法求权重
% 第一步：将A的元素按照行相乘得到一个新的列向量
clc;A
Prduct_A = prod(A,2)
% prod函数和sum函数类似，一个用于乘，一个用于加  dim = 2 维度是行

% 第二步：将新的向量的每个分量开n次方
Prduct_n_A = Prduct_A .^ (1/n)
% 这里对每个元素进行乘方操作，因此要加.号哦。  ^符号表示乘方哦  这里是开n次方，所以我们等价求1/n次方

% 第三步：对该列向量进行归一化即可得到权重向量
% 将这个列向量中的每一个元素除以这一个向量的和即可
disp('几何平均法求权重的结果为：');
disp(Prduct_n_A ./ sum(Prduct_n_A))

%% 方法3：特征值法求权重
% 第一步：求出矩阵A的最大特征值以及其对应的特征向量
clc
[V,D] = eig(A)    %V是特征向量, D是由特征值构成的对角矩阵（除了对角线元素外，其余位置元素全为0）
Max_eig = max(max(D)) %也可以写成max(D(:))哦~
% 那么怎么找到最大特征值所在的位置了？ 需要用到find函数，它可以用来返回向量或者矩阵中不为0的元素的位置索引。
% 那么问题来了，我们要得到最大特征值的位置，就需要将包含所有特征值的这个对角矩阵D中，不等于最大特征值的位置全变为0
% 这时候可以用到矩阵与常数的大小判断运算
D == Max_eig
[r,c] = find(D == Max_eig , 1)
% 找到D中第一个与最大特征值相等的元素的位置，记录它的行和列。

% 第二步：对求出的特征向量进行归一化即可得到我们的权重
V(:,c)
disp('特征值法求权重的结果为：');
disp( V(:,c) ./ sum(V(:,c)) )
% 我们先根据上面找到的最大特征值的列数c找到对应的特征向量，然后再进行标准化。

%% 计算一致性比例CR
clc
CI = (Max_eig - n) / (n-1);
RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];  %注意哦，这里的RI最多支持 n = 15
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
    disp('因为CR < 0.10，所以该判断矩阵A的一致性可以接受!');
else
    disp('注意：CR >= 0.10，因此该判断矩阵A需要进行修改!');
end

例题展示

img

img

img

img

img

img

模糊综合评价模型

核心在于模糊的概念

概述

数学归纳法

image-20240128192713567

数学的量的划分

确定性

不确定性

image-20240128192829255

模糊数学

image-20240128192918227

经典集合和模糊集合的基本概念

经典集合

image-20240128193114838

模糊集合：描述模糊性概念的集合

image-20240128193422098

表示方法

image-20240128193903017

image-20240128194009677

隶属函数的三种确定方法

模糊统计法

用的比较少的模糊统计法

找特别多人

image-20240128194409356

借助已有的客观尺度

合适的指标，并能收集到数据

image-20240128194540182

指派法

有很多分布，主要是梯形分布

image-20240128195038097

image-20240128195025001

例题一

image-20240128195203066

例题二

image-20240128195305070

梯形分布

image-20240128195426402

应用：模糊综合评价

image-20240128195517785

知识点：

确定因素集：相关性之间要不太强

确定评语集：由于每个指标的评价值不同，形成不同的等级。

image-20240128195716703

确定权重：Delphi法，专家法。

无数据：层次分析法

有数据：熵权法

权重也需要归一化，确定的时候注意

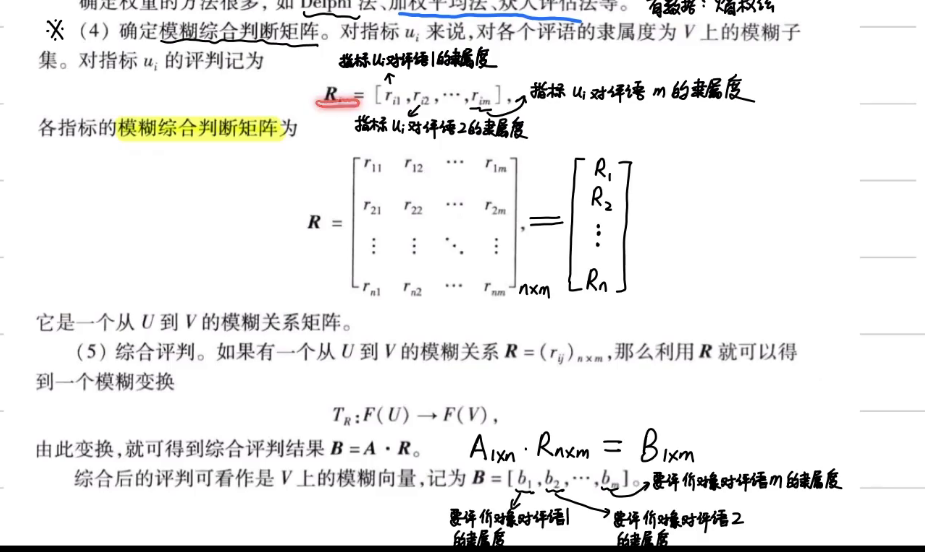
模糊综合判断矩阵

解释：第一列表示各个指标对于评语1的隶属度

image-20240128200239957

例题：

image-20240128200407651

层次分析法得到权重

image-20240128200513147

image-20240128200537561

一级模糊综合评价模型例子

一

image-20240128200742371

SO2的隶属度计算

image-20240128200932155

同理：

image-20240128201002529

AR=

二

image-20240128201137546

image-20240128201342001

image-20240128201252683

多级模糊综合评价模型的引入

image-20240128202425981

image-20240128202456942

image-20240128202620958

image-20240128202637622

重复1的步骤2遍即可

三极模糊综合评价模型

image-20240128202134589

同理

image-20240128203040666

image-20240128203115836

image-20240128203122965

基于熵权法对Topsis模型的修正

image-20240129163013762

找出最优与最最差，比较程度

常用的综合评价方法，充分利用原始数据

指标很多数据已知的评分问题

层次分析不适合指标太多的，都是主观的，没数据

指标的处理（正向化）

效益类

极小类

中间型

区间型

指标的处理

img

标准化

image-20240129163301619

image-20240129163316013

计算距离与得分

image-20240129163340888

例子：

image-20240129163405891

image-20240129163431275

第一步

image-20240129163513843

image-20240129163522594

image-20240129163529473

image-20240129163536903

第二步

image-20240129163548186

第三步

计算各评价对象与最优方案的贴近程度。正其中

的取值范围为[0,1]，越接近1表明样本评分越好。

image-20240129163558967

第四步

进行排序即可

代码

%%  第一步：把数据复制到工作区，并将这个矩阵命名为X
% （1）在工作区右键，点击新建（Ctrl+N)，输入变量名称为X
% （2）在Excel中复制数据，再回到Matlab中右键，点击粘贴Excel数据（Ctrl+Shift+V）
% （3）关掉这个窗口，点击X变量，右键另存为，保存为mat文件（下次就不用复制粘贴了，只需使用load命令即可加载数据）
% （4）注意，代码和数据要放在同一个目录下哦，且Matlab的当前文件夹也要是这个目录。
clear;clc
load data_water_quality.mat
%% 注意：如果提示: 错误使用 load，无法读取文件 'data_water_quality.mat'。没有此类文件或目录。
% 那么原因是因为你的Matlab的当前文件夹中不存在这个文件
% 可以使用cd函数修改Matlab的当前文件夹
% 比如说，我的代码和数据放在了: D:第2讲.TOPSIS法（优劣解距离法）/代码和例题数据
% 那么我就可以输入命令：
% cd 'D:第2讲.TOPSIS法（优劣解距离法）/代码和例题数据'
% 也可以看我更新的视频：“更新9_Topsis代码为什么运行失败_得分结果怎么可视化以及权重的确定如何更加准确”，里面有介绍

%%  第二步：判断是否需要正向化
[n,m] = size(X);
disp(['共有' num2str(n) '个评价对象, ' num2str(m) '个评价指标']) 
Judge = input(['这' num2str(m) '个指标是否需要经过正向化处理，需要请输入1 ，不需要输入0：  ']);

if Judge == 1
    Position = input('请输入需要正向化处理的指标所在的列，例如第2、3、6三列需要处理，那么你需要输入[2,3,6]： '); %[2,3,4]
    disp('请输入需要处理的这些列的指标类型（1：极小型， 2：中间型， 3：区间型） ')
    Type = input('例如：第2列是极小型，第3列是区间型，第6列是中间型，就输入[1,3,2]：  '); %[2,1,3]
    % 注意，Position和Type是两个同维度的行向量
    for i = 1 : size(Position,2)  %这里需要对这些列分别处理，因此我们需要知道一共要处理的次数，即循环的次数
        X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));
    % Positivization是我们自己定义的函数，其作用是进行正向化，其一共接收三个参数
    % 第一个参数是要正向化处理的那一列向量 X(:,Position(i))   回顾上一讲的知识，X(:,n)表示取第n列的全部元素
    % 第二个参数是对应的这一列的指标类型（1：极小型， 2：中间型， 3：区间型）
    % 第三个参数是告诉函数我们正在处理的是原始矩阵中的哪一列
    % 该函数有一个返回值，它返回正向化之后的指标，我们可以将其直接赋值给我们原始要处理的那一列向量
    end
    disp('正向化后的矩阵 X =  ')
    disp(X)
end

%% 第三步：对正向化后的矩阵进行标准化
Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);
disp('标准化矩阵 Z = ')
disp(Z)

%% 第四步：计算与最大值的距离和最小值的距离，并算出得分
D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ],2) .^ 0.5;   % D+ 与最大值的距离向量
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ],2) .^ 0.5;   % D- 与最小值的距离向量
S = D_N ./ (D_P+D_N);    % 未归一化的得分
disp('最后的得分为：')
stand_S = S / sum(S)
[sorted_S,index] = sort(stand_S ,'descend')

% function [输出变量] = 函数名称(输入变量）  
% 函数的中间部分都是函数体
% 函数的最后要用end结尾
% 输出变量和输入变量可以有多个，用逗号隔开
% function [a,b,c]=test(d,e,f)
%     a=d+e;
%     b=e+f;
%     c=f+d;
% end
% 自定义的函数要单独放在一个m文件中，不可以直接放在主函数里面（和其他大多数语言不同）

function [posit_x] = Positivization(x,type,i)
% 输入变量有三个：
% x：需要正向化处理的指标对应的原始列向量
% type： 指标的类型（1：极小型， 2：中间型， 3：区间型）
% i: 正在处理的是原始矩阵中的哪一列
% 输出变量posit_x表示：正向化后的列向量
    if type == 1  %极小型
        disp(['第' num2str(i) '列是极小型，正在正向化'] )
        posit_x = Min2Max(x);  %调用Min2Max函数来正向化
        disp(['第' num2str(i) '列极小型正向化处理完成'] )
        disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~')
    elseif type == 2  %中间型
        disp(['第' num2str(i) '列是中间型'] )
        best = input('请输入最佳的那一个值： ');
        posit_x = Mid2Max(x,best);
        disp(['第' num2str(i) '列中间型正向化处理完成'] )
        disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~')
    elseif type == 3  %区间型
        disp(['第' num2str(i) '列是区间型'] )
        a = input('请输入区间的下界： ');
        b = input('请输入区间的上界： '); 
        posit_x = Inter2Max(x,a,b);
        disp(['第' num2str(i) '列区间型正向化处理完成'] )
        disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~')
    else
        disp('没有这种类型的指标，请检查Type向量中是否有除了1、2、3之外的其他值')
    end
end



最大值
Intermax
function [posit_x] = Inter2Max(x,a,b)
    r_x = size(x,1);  % row of x 
    M = max([a-min(x),max(x)-b]);
    posit_x = zeros(r_x,1);   %zeros函数用法: zeros(3)  zeros(3,1)  ones(3)
    % 初始化posit_x全为0  初始化的目的是节省处理时间
    for i = 1: r_x
        if x(i) < a
           posit_x(i) = 1-(a-x(i))/M;
        elseif x(i) > b
           posit_x(i) = 1-(x(i)-b)/M;
        else
           posit_x(i) = 1;
        end
    end
end

MId2max
function [posit_x] = Mid2Max(x,best)
    M = max(abs(x-best));
    posit_x = 1 - abs(x-best) / M;
end




min2max
function [posit_x] = Min2Max(x)
    posit_x = max(x) - x;
     %posit_x = 1 ./ x;    %如果x全部都大于0，也可以这样正向化
end

例题

image-20240129164107645

image-20240129164125974

image-20240129164135640

熵权法新鲜出炉

image-20240131172123873

image-20240131172131388

image-20240131172140403

image-20240131172154180

%%  第一步：把数据复制到工作区，并将这个矩阵命名为X
% （1）在工作区右键，点击新建（Ctrl+N)，输入变量名称为X
% （2）在Excel中复制数据，再回到Matlab中右键，点击粘贴Excel数据（Ctrl+Shift+V）
% （3）关掉这个窗口，点击X变量，右键另存为，保存为mat文件（下次就不用复制粘贴了，只需使用load命令即可加载数据）
% （4）注意，代码和数据要放在同一个目录下哦。
clear;clc
load data_water_quality.mat

%%  第二步：判断是否需要正向化
[n,m] = size(X);
disp(['共有' num2str(n) '个评价对象, ' num2str(m) '个评价指标']) 
Judge = input(['这' num2str(m) '个指标是否需要经过正向化处理，需要请输入1 ，不需要输入0：  ']);

if Judge == 1
    Position = input('请输入需要正向化处理的指标所在的列，例如第2、3、6三列需要处理，那么你需要输入[2,3,6]： '); %[2,3,4]
    disp('请输入需要处理的这些列的指标类型（1：极小型， 2：中间型， 3：区间型） ')
    Type = input('例如：第2列是极小型，第3列是区间型，第6列是中间型，就输入[1,3,2]：  '); %[2,1,3]
    % 注意，Position和Type是两个同维度的行向量
    for i = 1 : size(Position,2)  %这里需要对这些列分别处理，因此我们需要知道一共要处理的次数，即循环的次数
        X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));
    % Positivization是我们自己定义的函数，其作用是进行正向化，其一共接收三个参数
    % 第一个参数是要正向化处理的那一列向量 X(:,Position(i))   回顾上一讲的知识，X(:,n)表示取第n列的全部元素
    % 第二个参数是对应的这一列的指标类型（1：极小型， 2：中间型， 3：区间型）
    % 第三个参数是告诉函数我们正在处理的是原始矩阵中的哪一列
    % 该函数有一个返回值，它返回正向化之后的指标，我们可以将其直接赋值给我们原始要处理的那一列向量
    end
    disp('正向化后的矩阵 X =  ')
    disp(X)
end
%% 作业：在这里增加是否需要算加权
% 补充一个基础知识：m*n维的矩阵A 点乘 n维行向量B，等于这个A的每一行都点乘B
% （注意：2017以及之后版本的Matlab才支持，老版本Matlab会报错）
% % 假如原始数据为：
%   A=[1, 2, 3;
%        2, 4, 6] 
% % 权重矩阵为：
%   B=[ 0.2, 0.5 ,0.3 ] 
% % 加权后为：
%   C=A .* B
%     0.2000    1.0000    0.9000
%     0.4000    2.0000    1.8000
% 类似的，还有矩阵和向量的点除， 大家可以自己试试计算A ./ B
% 注意，矩阵和向量没有 .- 和 .+ 哦 ，大家可以试试，如果计算A.+B 和 A.-B会报什么错误。

%% 这里补充一个小插曲
% % 在上一讲层次分析法的代码中，我们可以优化以下的语句：
% % Sum_A = sum(A);
% % SUM_A = repmat(Sum_A,n,1);
% % Stand_A = A ./ SUM_A;
% % 事实上，我们把第三行换成：Stand_A = A ./ Sum_A; 也是可以的哦 
% % (再次强调，新版本的Matlab才能运行哦)

%% 第三步：对正向化后的矩阵进行标准化
Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);
disp('标准化矩阵 Z = ')
disp(Z)


%% 让用户判断是否需要增加权重
disp("请输入是否需要增加权重向量，需要输入1，不需要输入0")
Judge = input('请输入是否需要增加权重： ');
if Judge == 1
    Judge = input('使用熵权法确定权重请输入1，否则输入0： ');
    if Judge == 1
        if sum(sum(Z<0)) >0   % 如果之前标准化后的Z矩阵中存在负数，则重新对X进行标准化
            disp('原来标准化得到的Z矩阵中存在负数，所以需要对X重新标准化')
            for i = 1:n
                for j = 1:m
                    Z(i,j) = [X(i,j) - min(X(:,j))] / [max(X(:,j)) - min(X(:,j))];
                end
            end
            disp('X重新进行标准化得到的标准化矩阵Z为:  ')
            disp(Z)
        end
        weight = Entropy_Method(Z);
        disp('熵权法确定的权重为：')
        disp(weight)
    else
        disp(['如果你有3个指标，你就需要输入3个权重，例如它们分别为0.25,0.25,0.5, 则你需要输入[0.25,0.25,0.5]']);
        weight = input(['你需要输入' num2str(m) '个权数。' '请以行向量的形式输入这' num2str(m) '个权重: ']);
        OK = 0;  % 用来判断用户的输入格式是否正确
        while OK == 0 
            if abs(sum(weight) -1)<0.000001 && size(weight,1) == 1 && size(weight,2) == m  % 注意，Matlab中浮点数的比较要小心
                OK =1;
            else
                weight = input('你输入的有误，请重新输入权重行向量: ');
            end
        end
    end
else
    weight = ones(1,m) ./ m ; %如果不需要加权重就默认权重都相同，即都为1/m
end


%% 第四步：计算与最大值的距离和最小值的距离，并算出得分
D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ] .* repmat(weight,n,1) ,2) .^ 0.5;   % D+ 与最大值的距离向量
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ] .* repmat(weight,n,1) ,2) .^ 0.5;   % D- 与最小值的距离向量
S = D_N ./ (D_P+D_N);    % 未归一化的得分
disp('最后的得分为：')
stand_S = S / sum(S)
[sorted_S,index] = sort(stand_S ,'descend')

% A = magic(5)  % 幻方矩阵
% M = magic(n)返回由1到n^2的整数构成并且总行数和总列数相等的n×n矩阵。阶次n必须为大于或等于3的标量。
% sort(A)若A是向量不管是列还是行向量，默认都是对A进行升序排列。sort(A)是默认的升序，而sort(A,'descend')是降序排序。
% sort(A)若A是矩阵，默认对A的各列进行升序排列
% sort(A,dim)
% dim=1时等效sort(A)
% dim=2时表示对A中的各行元素升序排列
% A = [2,1,3,8]
% Matlab中给一维向量排序是使用sort函数：sort（A），排序是按升序进行的，其中A为待排序的向量；
% 若欲保留排列前的索引，则可用 [sA,index] = sort(A,'descend') ，排序后，sA是排序好的向量，index是向量sA中对A的索引。
% sA  =  8     3     2     1
% index =  4     3     1     2

灰色关联分析（美赛不用）

完结撒花