集合

题单简介

有时候，我们并不关心数据之间的前后关系，也不关心数据的层次关系。一些确定元素只是单纯的聚集在一起，这样的元素聚集体被称为集合。

当希望知道某个数据是否存在一个集合中，或者两个元素是否在同一个集合中时，就需要使用一些集合数据结构来维护集合元素之间的关系。

亲戚

题目背景

若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。

题目描述

规定：\(x\) 和 \(y\) 是亲戚，\(y\) 和 \(z\) 是亲戚，那么 \(x\) 和 \(z\) 也是亲戚。如果 \(x\)，\(y\) 是亲戚，那么 \(x\) 的亲戚都是 \(y\) 的亲戚，\(y\) 的亲戚也都是 \(x\) 的亲戚。

输入格式

第一行：三个整数 \(n,m,p\)，（\(n,m,p \le 5000\)），分别表示有 \(n\) 个人，\(m\) 个亲戚关系，询问 \(p\) 对亲戚关系。

以下 \(m\) 行：每行两个数 \(M_i\)，\(M_j\)，\(1 \le M_i,~M_j\le n\)，表示 \(M_i\) 和 \(M_j\) 具有亲戚关系。

接下来 \(p\) 行：每行两个数 \(P_i,P_j\)，询问 \(P_i\) 和 \(P_j\) 是否具有亲戚关系。

输出格式

\(p\) 行，每行一个 Yes 或 No。表示第 \(i\) 个询问的答案为“具有”或“不具有”亲戚关系。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6

样例输出 #1

1
2
3
Yes
Yes
No
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
/*
并查集，主要用于解决一些元素分组的问题。它管理一系列不相交的集合，并支持两种操作：

合并（Union）：把两个不相交的集合合并为一个集合。
查询（Find）：查询两个元素是否在同一个集合中。
*/
#include<iostream>
using namespace std;
int f[1000000];
int find(int x)
{
	if (x==f[x])
	{
		return x;
	}
	return f[x]=find(f[x]);
}
int main()
{
	int n, m, p,x,y;
	cin >> n >> m >> p;

	for (int i = 1; i <=n; i++)
	{
		f[i] = i;
	}
    /*
  对于只有一个元素的集合，代表元素自然是唯一的那个元素
    */
	for (int i = 1; i <=m ; i++)
	{
		cin >> x >> y;
		int fx = find(x);
		int fy = find(y);
		if (fx!=fy)
		{
			f[fx] = fy;//合并操作
		}
	}
	for (int i = 1; i <=p ; i++)
	{
		cin >> x >> y;
		int fx = find(x);
		int fy = find(y);
		if (fx==fy)
		{
			cout << "Yes" << "\n";
		}
		else
		{
			cout << "No" << "\n";
		}
	}
}

村村通

题目描述

某市调查城镇交通状况，得到现有城镇道路统计表。表中列出了每条道路直接连通的城镇。市政府 "村村通工程" 的目标是使全市任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要相互之间可达即可）。请你计算出最少还需要建设多少条道路？

输入格式

输入包含若干组测试数据，每组测试数据的第一行给出两个用空格隔开的正整数，分别是城镇数目 \(n\) 和道路数目 \(m\) ；随后的 \(m\) 行对应 \(m\) 条道路，每行给出一对用空格隔开的正整数，分别是该条道路直接相连的两个城镇的编号。简单起见，城镇从 \(1\) 到 \(n\) 编号。

注意：两个城市间可以有多条道路相通。

在输入数据的最后，为一行一个整数 \(0\)，代表测试数据的结尾。

输出格式

对于每组数据，对应一行一个整数。表示最少还需要建设的道路数目。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
10
11
12
4 2
1 3
4 3
3 3
1 2
1 3
2 3
5 2
1 2
3 5
999 0
0

样例输出 #1

1
2
3
4
1
0
2
998

提示

数据规模与约定

对于 \(100\%\) 的数据，保证 \(1 \le n < 1000\) 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<iostream>
using namespace std;
int f[1000000];
int find(int x)
{
	if (f[x]==x)
	{
		return x;
	}
	else
	{
		return f[x]=find(f[x]);
	}
}
int main()
{
	int n, m, x, y;
	cin >> n;
	while (n!=0)
	{
		cin >> m;
		int ans = -1;
		for (int i = 1; i <= n; i++)
		{
			f[i] = i;
		}
		for (int i = 1; i <=m ; i++)
		{
			cin >> x >> y;
			int fx = find(x);
			int fy = find(y);
			if (fx!=fy)
			{
				f[fx] = fy;
			}
		}
		for (int i = 1; i <=n ; i++)
		{
			if (f[i]==i)
			{
				ans++;
			}
		}
		cout << ans << '\n';
		cin >> n;
	}
}

【模板】字符串哈希

题目描述

如题，给定 \(N\) 个字符串（第 \(i\) 个字符串长度为 \(M_i\)，字符串内包含数字、大小写字母，大小写敏感），请求出 \(N\) 个字符串中共有多少个不同的字符串。

友情提醒：如果真的想好好练习哈希的话，请自觉。

输入格式

第一行包含一个整数 \(N\)，为字符串的个数。

接下来 \(N\) 行每行包含一个字符串，为所提供的字符串。

输出格式

输出包含一行，包含一个整数，为不同的字符串个数。

样例 #1

样例输入 #1

1
2
3
4
5
6
5
abc
aaaa
abc
abcc
12345

样例输出 #1

1
4

提示

对于 \(30\%\) 的数据：\(N\leq 10\)，\(M_i≈6\)，\(Mmax\leq 15\)。

对于 \(70\%\) 的数据：\(N\leq 1000\)，\(M_i≈100\)，\(Mmax\leq 150\)。

对于 \(100\%\) 的数据：\(N\leq 10000\)，\(M_i≈1000\)，\(Mmax\leq 1500\)。

样例说明：

样例中第一个字符串(abc)和第三个字符串(abc)是一样的，所以所提供字符串的集合为{aaaa,abc,abcc,12345}，故共计4个不同的字符串。

Tip： 感兴趣的话，你们可以先看一看以下三题：

BZOJ3097：http://www.lydsy.com/JudgeOnline/problem.php?id=3097

BZOJ3098：http://www.lydsy.com/JudgeOnline/problem.php?id=3098

BZOJ3099：http://www.lydsy.com/JudgeOnline/problem.php?id=3099

如果你仔细研究过了（或者至少仔细看过AC人数的话），我想你一定会明白字符串哈希的正确姿势的_

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include<map>
#include<iostream>
#include<string>
using namespace std;
int ans, n;
map<string,int>m;

int main()
{
	cin >> n;
	string s;

	for (int i = 1; i <=n ; i++)
	{
		cin >> s;
		m[s] = 1;

	}
	cout << m.size();
}


//或者说
    #include<bits/stdc++.h>
using namespace std;
set<string> a;
int main()
{
    string p;
    int n,i;
    cin>>n;
    for(i=0;i<n;i++)
    {
    	cin>>p;
    	a.insert(p);
	}
	cout<<a.size();
}

//或者说
#include<bits/stdc++.h>
using namespace std;
list<string>q;//链表
int n;
int main()
{
	cin >> n;
	for (int i=1; i<=n; i++)
	{
		string s;
		cin >> s;//输入
		q.push_front(s);//加入链表
	}
	q.sort();//排序
	q.unique();//去重
	cout << q.size();//输出
}

//又或者说
#include<iostream>
using namespace std;
typedef unsigned long long ull;
ull base=131;
ull a[10010];
char s[10010];
int n,ans=1;
int prime=233317; 
ull mod=212370440130137957ll;
ull hashe(char s[])
{
 int len=strlen(s);
 ull ans=0;
 for (int i=0;i<len;i++)
 ans=(ans*base+(ull)s[i])%mod+prime;
 return ans;
}
int main()
{
cin>>n;
 for(int i=1;i<=n;i++)
 {
 cin>>s;
 	a[i]=hashe(s);
 }
 sort(a+1,a+n+1);
 for(int i=1;i<n;i++)
 {
 	if(a[i]!=a[i+1])
 	ans++;
 }
cout<<ans;
}

[USACO16DEC] Cities and States S

题目描述

Farmer John 有若干头奶牛。为了训练奶牛们的智力，Farmer John 在谷仓的墙上放了一张美国地图。地图上表明了每个城市及其所在州的代码（前两位大写字母）。

由于奶牛在谷仓里花了很多时间看这张地图，他们开始注意到一些奇怪的关系。例如，FLINT 的前两个字母就是 MIAMI 所在的 FL 州，MIAMI 的前两个字母则是 FLINT 所在的 MI 州。
确切地说，对于两个城市，它们的前两个字母互为对方所在州的名称。

我们称两个城市是一个一对「特殊」的城市，如果他们具有上面的特性，并且来自不同的州。对于总共 \(N\) 座城市，奶牛想知道有多少对「特殊」的城市存在。请帮助他们解决这个有趣的地理难题！

输入格式

输入共 \(N + 1\) 行。

第一行一个正整数 \(N\)，表示地图上的城市的个数。
接下来 \(N\) 行，每行两个字符串，分别表示一个城市的名称（\(2 \sim 10\) 个大写字母）和所在州的代码（\(2\) 个大写字母）。同一个州内不会有两个同名的城市。

输出格式

输出共一行一个整数，代表特殊的城市对数。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
6
MIAMI FL
DALLAS TX
FLINT MI
CLEMSON SC
BOSTON MA
ORLANDO FL

样例输出 #1

1
1

提示

数据规模与约定

对于 \(100\%\) 的数据，\(1 \leq N \leq 2 \times 10 ^ 5\)，城市名称长度不超过 \(10\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<bits/stdc++.h>
using namespace std;
map<int,int>mmp[100005];
int n,ans;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++){
        string a,b;
        cin>>a>>b;
        int A=a[0]*26+a[1];
        int B=b[0]*26+b[1];
        ans+=mmp[B][A];
        if(A==B)ans-=mmp[A][B];
        mmp[A][B]++;
    }
  cout<<ans;
}

【深基17.例5】木材仓库

题目描述

博艾市有一个木材仓库，里面可以存储各种长度的木材，但是保证没有两个木材的长度是相同的。作为仓库负责人，你有时候会进货，有时候会出货，因此需要维护这个库存。有不超过 100000 条的操作：

  • 进货，格式1 Length：在仓库中放入一根长度为 Length(不超过 \(10^9\)) 的木材。如果已经有相同长度的木材那么输出Already Exist。
  • 出货，格式2 Length：从仓库中取出长度为 Length 的木材。如果没有刚好长度的木材，取出仓库中存在的和要求长度最接近的木材。如果有多根木材符合要求，取出比较短的一根。输出取出的木材长度。如果仓库是空的，输出Empty。

输入格式

输出格式

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
7
1 1
1 5
1 3
2 3
2 3
2 3
2 3

样例输出 #1

1
2
3
4
3
1
5
Empty
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
begin()     　　 返回set容器的第一个元素

end() 　　　　 返回set容器的最后一个元素

clear()   　　  删除set容器中的所有的元素

empty() 　　　判断set容器是否为空

max_size() 　 返回set容器可能包含的元素最大个数

size() 　　　　 返回当前set容器中的元素个数

rbegin　　　　 返回的值和end()相同

rend()　　　　 返回的值和rbegin()相同
    
    
count() 用来查找set中某个某个键值出现的次数。这个函数在set并不是很实用，因为一个键值在set只可能出现0或1次，这样就变成了判断某一键值是否在set出现过了。

erase(iterator)  ,删除定位器iterator指向的值
    
find()  ，返回给定值值得定位器，如果没找到则返回end()。
    
insert(key_value); 将key_value插入到set中 ，返回值是pair<set<int>::iterator,bool>，bool标志着插入是否成功，而iterator代表插入的位置，若key_value已经在set中，则iterator表示的key_value在set中的位置。    

lower_bound(key_value) ，返回第一个大于等于key_value的定位器

upper_bound(key_value)，返回最后一个大于等于key_value的定位器    
    
#include<bits/stdc++.h> 
using namespace std;
int n, op, t;
set<int>::iterator lwb, l2, l3;
set<int> s;
int main(){
	cin >> n;
	for (int i = 1;i <= n;i ++){
		cin >> op >> t;
		if (op == 1){
			if (!s.insert(t).second) 
            {
                cout << "Already Exist\n";
            }
		}
		else {
			if (s.empty())
            {
				cout << "Empty\n";
				continue;
			}
			if (s.find(t) != s.end()) 
            {
                cout << t;
                s.erase(s.find(t));
            }
			else 
            {
				lwb = l2 = l3 = s.lower_bound(t);
				if (lwb == s.begin()) cout << *lwb, s.erase(lwb);//开端
				else if (lwb == s.end()) cout << *(-- l3), s.erase(l3);//终止
				else if (*lwb - t < t - *(-- l2)) cout << *(l3), s.erase(l3);//中间，需要斟酌
				else cout << *(-- l3), s.erase(l3);
			}
			cout <<'\n';
		}
	}
}

【深基17.例6】学籍管理

题目描述

您要设计一个学籍管理系统，最开始学籍数据是空的，然后该系统能够支持下面的操作（不超过 \(10^5\) 条）：

  • 插入与修改，格式1 NAME SCORE：在系统中插入姓名为 NAME(由字母和数字组成不超过 20 个字符的字符串，区分大小写) ，分数为 \(\texttt{SCORE}\)（\(0<\texttt{SCORE}<2^{31}\)） 的学生。如果已经有同名的学生则更新这名学生的成绩为 SCORE。如果成功插入或者修改则输出OK。
  • 查询，格式2 NAME：在系统中查询姓名为 NAME 的学生的成绩。如果没能找到这名学生则输出Not found，否则输出该生成绩。
  • 删除，格式3 NAME：在系统中删除姓名为 NAME 的学生信息。如果没能找到这名学生则输出Not found，否则输出Deleted successfully。
  • 汇总，格式4：输出系统中学生数量。

输入格式

输出格式

样例 #1

样例输入 #1

1
2
3
4
5
6
5
1 lxl 10
2 lxl
3 lxl
2 lxl
4

样例输出 #1

1
2
3
4
5
OK
10
Deleted successfully
Not found
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
map是一种描述“对应关系”的存储结构，就像函数一样
a.count(x)	判断x为下标的元素是不是在a中，是就返回1，不是就返回0
a.erase(x)	删除a中x为下标的元素
a.size()	返回a中元素的个数
a.clear()	清空a


#include<iostream>
#include<map>
#include<string>
using namespace std;
map< string, int > m;

int opt, score, n;
string name;
int main()
{
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> opt;
		if (opt==1)
		{
			cin >> name >> score;
			m[name] = score;
			cout << "OK" << "\n";
		}
		else if (opt==2)
		{
			cin >> name;
			if (m.find(name)==m.end())
			{
				cout << "Not found" << "\n";
			}
			else
			{
				cout << m[name] << "\n";
			}
		}
		else if (opt==3)
		{
			cin >> name;
			if (m.find(name)==m.end())
			{
				cout << "Not found" << "\n";
			}
			else
			{
				m.erase(name);
				cout << "Deleted successfully" << "\n";
			}
		}
		else
		{
			cout << m.size()<<"\n";
		}
	}
}

A-B 数对

题目背景

出题是一件痛苦的事情！

相同的题目看多了也会有审美疲劳，于是我舍弃了大家所熟悉的 A+B Problem，改用 A-B 了哈哈！

题目描述

给出一串正整数数列以及一个正整数 \(C\)，要求计算出所有满足 \(A - B = C\) 的数对的个数（不同位置的数字一样的数对算不同的数对）。

输入格式

输入共两行。

第一行，两个正整数 \(N,C\)。

第二行，\(N\) 个正整数，作为要求处理的那串数。

输出格式

一行，表示该串正整数中包含的满足 \(A - B = C\) 的数对的个数。

样例 #1

样例输入 #1

1
2
4 1
1 1 2 3

样例输出 #1

1
3

提示

对于 \(75\%\) 的数据，\(1 \leq N \leq 2000\)。

对于 \(100\%\) 的数据，\(1 \leq N \leq 2 \times 10^5\)，\(0 \leq a_i <2^{30}\)，\(1 \leq C < 2^{30}\)。

2017/4/29 新添数据两组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
//这里用的是滑动窗口
#include<bits/stdc++.h>
using namespace std;
const int N=1e7;
int a[N];
using ll=long long;
#define rep(i,a,n) for(int i=a;i<=n;i++)
int main()
{
int n;
cin>>n;
int  c;
cin>>c;
rep(i,1,n)
{
    cin>>a[i];
}
sort(a+1,a+1+n);
int l=0;
int r=0;
ll ans=0;
rep(i,1,n)
{
    while(a[i]>a[l]-c&&l<=n )
    {
        l++;
    }
    while(a[i]>=a[r]-c&&r<=n)
   {
    r++;
   }
   if(a[l]-a[i]==c)
   {
       ans += r - l;
   }

}
cout<<ans;
}

//想看映射可以看第一篇题解（）这里贴出来（）
      #include <iostream>
    #include <map>
    using namespace std;
    typedef long long LL;
    LL a[200001];
    map<LL,LL> m;//建立一个数字到出现次数的映射 map<num,times>
    //A-B=C --> A-C=B
    int main() {
        int n;
        LL c;
        LL ans=0;
        cin >> n >> c;
        for(int i=1;i<=n;i++) {
            cin >> a[i];
            m[a[i]]++;
            a[i]-=c;    
        } 
        for(int i=1;i<=n;i++) ans+=m[a[i]];
        cout << ans << endl;
        return 0;
}

保龄球

题目描述

DL 算缘分算得很烦闷，所以常常到体育馆去打保龄球解闷。因为他保龄球已经打了几十年了，所以技术上不成问题，于是他就想玩点新花招。

DL 的视力真的很不错，竟然能够数清楚在他前方十米左右每个位置的瓶子的数量。他突然发现这是一个炫耀自己好视力的借口——他看清远方瓶子的个数后从某个位置发球，这样就能打倒一定数量的瓶子。

  1. \(\bigcirc \bigcirc \bigcirc\)

  2. \(\bigcirc \bigcirc \bigcirc\ \bigcirc\)

  3. \(\bigcirc\)

  4. \(\bigcirc\ \bigcirc\)

如上图，每个 “\(\bigcirc\)” 代表一个瓶子。如果 DL 想要打倒 \(3\) 个瓶子就在 \(1\) 位置发球，想要打倒 \(4\) 个瓶子就在 \(2\) 位置发球。

现在他想要打倒 \(m\) 个瓶子。他告诉你每个位置的瓶子数，请你给他一个发球位置。

输入格式

第一行包含一个正整数 \(n\)，表示位置数。

第二行包含 \(n\) 个正整数 \(a_i\) ，表示第 \(i\) 个位置的瓶子数，保证各个位置的瓶子数不同。

第三行包含一个正整数 \(Q\)，表示 DL 发球的次数。

第四行至文件末尾，每行包含一个正整数 \(m\)，表示 DL 需要打倒 \(m\) 个瓶子。

输出格式

共 \(Q\) 行。每行包含一个整数，第 \(i\) 行的整数表示 DL 第 \(i\) 次的发球位置。若无解，则输出 \(0\)。

样例 #1

样例输入 #1

1
2
3
4
5
5
1 2 4 3 5
2
4
7

样例输出 #1

1
2
3
0

提示

【数据范围】

对于 \(50\%\) 的数据，\(1 \leq n, Q \leq 1000, 1 \leq a_i, m \leq 10^5\)。

对于 \(100\%\) 的数据，\(1 \leq n,Q \leq 100000, 1 \leq a_i, m \leq 10^9\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<algorithm>	
#include<string>
#include<iostream>
#include<map>
using namespace std;
map<int, int>m;
int n, t;
int main()
{
	cin >> n;
	for (int i = 1; i <=n ; i++)
	{
		cin >> t;
		m[t] = i;
	}
	cin >> n;
	for (int i = 0; i <n; i++)
	{
		cin >> t;
		if (m.find(t)==m.end())
		{
			cout << "0" << '\n';
		}
		else
		{
			cout << m[t] << '\n';
		}
	}
}

[NOIP2010 提高组] 关押罪犯

题目背景

NOIP2010 提高组 T3

题目描述

S 城现有两座监狱，一共关押着 \(N\) 名罪犯，编号分别为 \(1\sim N\)。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久，如果客观条件具备则随时可能爆发冲突。我们用“怨气值”（一个正整数值）来表示某两名罪犯之间的仇恨程度，怨气值越大，则这两名罪犯之间的积怨越多。如果两名怨气值为 \(c\) 的罪犯被关押在同一监狱，他们俩之间会发生摩擦，并造成影响力为 \(c\) 的冲突事件。

每年年末，警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表，然后上报到 S 城 Z 市长那里。公务繁忙的 Z 市长只会去看列表中的第一个事件的影响力，如果影响很坏，他就会考虑撤换警察局长。

在详细考察了 \(N\) 名罪犯间的矛盾关系后，警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配，以求产生的冲突事件影响力都较小，从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨，那么他们一定会在每年的某个时候发生摩擦。

那么，应如何分配罪犯，才能使 Z 市长看到的那个冲突事件的影响力最小？这个最小值是多少？

输入格式

每行中两个数之间用一个空格隔开。第一行为两个正整数 \(N,M\)，分别表示罪犯的数目以及存在仇恨的罪犯对数。接下来的 \(M\) 行每行为三个正整数 \(a_j,b_j,c_j\)，表示 \(a_j\) 号和 \(b_j\) 号罪犯之间存在仇恨，其怨气值为 \(c_j\)。数据保证 \(1<a_j\leq b_j\leq N, 0 < c_j\leq 10^9\)，且每对罪犯组合只出现一次。

输出格式

共一行，为 Z 市长看到的那个冲突事件的影响力。如果本年内监狱中未发生任何冲突事件，请输出 0。

样例 #1

样例输入 #1

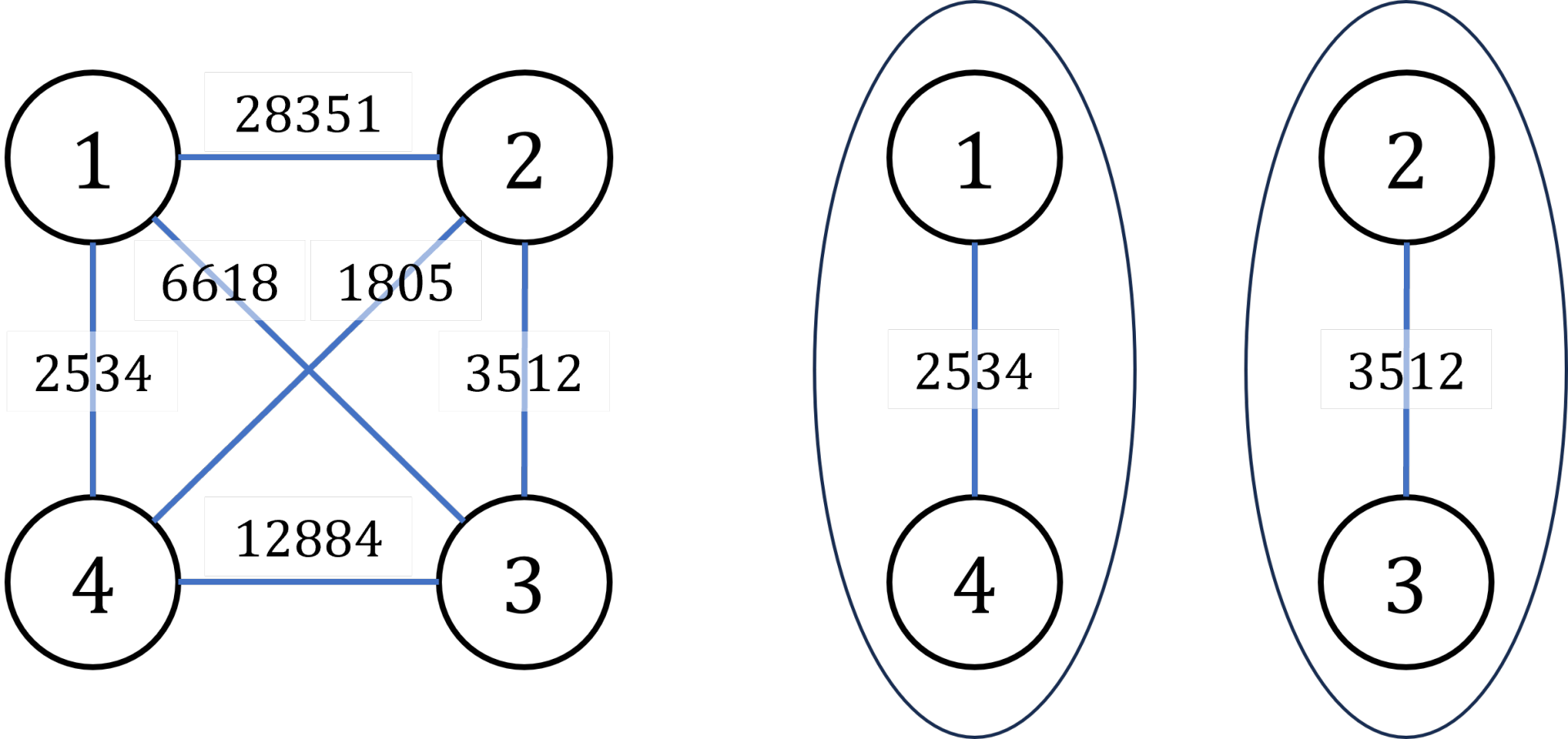
1
2
3
4
5
6
7
4 6
1 4 2534
2 3 3512
1 2 28351
1 3 6618
2 4 1805
3 4 12884

样例输出 #1

1
3512

提示

输入输出样例说明

罪犯之间的怨气值如下面左图所示，右图所示为罪犯的分配方法，市长看到的冲突事件影响力是 \(3512\)（由 \(2\) 号和 \(3\) 号罪犯引发）。其他任何分法都不会比这个分法更优。

数据范围

对于 \(30\%\) 的数据有 \(N\leq 15\)。

对于 \(70\%\) 的数据有 \(N\leq 2000,M\leq 50000\)。

对于 \(100\%\) 的数据有 \(N\leq 20000,M\leq 100000\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
//先排序
//当两个人出现问题时候再弄走
#include<bits/stdc++.h>
using namespace std;
int n,m,f[40001],x,y;
struct data
{
    int a,b,c;
} e[100001];
int gz( data a,data b)
{
    if(a.c>b.c)return 1;
    else return 0;
}
int find(int x)
{
    return f[x]==x?x:f[x]=find(f[x]);
}
int main()
{
  cin>>n>>m;
    for(int i=1; i<=m; i++)
      cin>>e[i].a>>e[i].b>>e[i].c;
    for(int i=1; i<=n*2; i++)
        f[i]=i;
    sort(e+1,e+m+1,gz);
    for(int i=1; i<=m; i++)
    {
        x=find(e[i].a);
        y=find(e[i].b);
        if(x==y)
        {
          cout<<e[i].c<<'\n';
            return 0;
        }
        f[y] = find(e[i].a + n);
        f[x] = find(e[i].b + n);
    }
 cout<<0;
 }

集合

集合

题目描述

Caima 给你了所有 \([a,b]\) 范围内的整数。一开始每个整数都属于各自的集合。每次你需要选择两个属于不同集合的整数，如果这两个整数拥有大于等于 \(p\) 的公共质因数，那么把它们所在的集合合并。

重复如上操作，直到没有可以合并的集合为止。

现在 Caima 想知道，最后有多少个集合。

输入格式

一行，共三个整数 \(a,b,p\)，用空格隔开。

输出格式

一个数，表示最终集合的个数。

样例 #1

样例输入 #1

1
10 20 3

样例输出 #1

1
7

提示

样例 1 解释

对于样例给定的数据，最后有 \(\{10,20,12,15,18\},\{13\},\{14\},\{16\},\{17\},\{19\},\{11\}\) 共 \(7\) 个集合，所以输出应该为 \(7\)。

数据规模与约定

  • 对于 \(80\%\) 的数据，\(1 \leq a \leq b \leq 10^3\)。
  • 对于 \(100%\) 的数据，\(1 \leq a \leq b \leq 10^5,2 \leq p \leq b\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <bits/stdc++.h>
using namespace std;
const int N=100010;
int f[N],a,b,p,ans;
bool np[N];
int find(int x)
{
	return x==f[x]?x:f[x]=find(f[x]);
}
int main()
{
	int i,j;
	cin>>a>>b>>p;
	ans=b-a+1; 
	for (i=a;i<=b;++i)
	{
		f[i]=i;
	}	
	for (i=2;i<=b;++i) //埃氏筛
	{
		if (!np[i])
		{
			if (i>=p) //如果当前质数大于p才合并
			{
				for (j=i*2;j<=b;j+=i)
				{
					np[j]=true;
					if (j-i>=a&&find(j)!=find(j-i)) 
					{
						f[find(j)]=find(j-i);
						--ans;
					}
				}
			}
			else
			{
				for (j=i*2;j<=b;j+=i)
				{
					np[j]=true;
				}
			}
		}
	}	
	cout<<ans;
}

[BOI2003] 团伙

题目描述

现在有 \(n\) 个人，他们之间有两种关系：朋友和敌人。我们知道：

  • 一个人的朋友的朋友是朋友
  • 一个人的敌人的敌人是朋友

现在要对这些人进行组团。两个人在一个团体内当且仅当这两个人是朋友。请求出这些人中最多可能有的团体数。

输入格式

第一行输入一个整数 \(n\) 代表人数。

第二行输入一个整数 \(m\) 表示接下来要列出 \(m\) 个关系。

接下来 \(m\) 行，每行一个字符 \(opt\) 和两个整数 \(p,q\)，分别代表关系（朋友或敌人），有关系的两个人之中的第一个人和第二个人。其中 \(opt\) 有两种可能：

  • 如果 \(opt\) 为 F，则表明 \(p\) 和 \(q\) 是朋友。
  • 如果 \(opt\) 为 E，则表明 \(p\) 和 \(q\) 是敌人。

输出格式

一行一个整数代表最多的团体数。

样例 #1

样例输入 #1

1
2
3
4
5
6
6
4
E 1 4
F 3 5
F 4 6
E 1 2

样例输出 #1

1
3

提示

对于 \(100\%\) 的数据，\(2 \le n \le 1000\)，\(1 \le m \le 5000\)，\(1 \le p,q \le n\)。

如果a和b是敌人，合并n+b和a，n+a和b

如果c和a是敌人，合并n+c和a，n+a和c

那么b和c就并在一起了

这样就符合了题目敌人的敌人是朋友的规则

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
//并查集与反集
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for(int i=a;i<=n;i++)
const int N=5e6;
using ll=long long;
int n,m;
int f[N];
int find(int x)
{
	if (x==f[x])
	{
		return x;
	}
	return f[x]=find(f[x]);
}
int main()
{
cin>>n>>m;
rep(i,1,2*n)
{
	f[i]=i;
}
		char c;
		int a,b;
rep(i,1,m)
	{
		cin>>c>>a>>b;
		if(c=='F')
		{
			f[find(a)]=find(b);
            //朋友
		}
		else
		{
			f[find(a+n)]=find(b);
			f[find(b+n)]=find(a);
            //敌人
		}
	}
	int ans=0;
	rep(i,1,n)
	{
		if(f[i]==i)
		{
			ans++;
		}
	}
	cout<<ans;
}

[NOI2015] 程序自动分析

题目描述

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设 \(x_1,x_2,x_3,\cdots\) 代表程序中出现的变量，给定 \(n\) 个形如 \(x_i=x_j\) 或 \(x_i\neq x_j\) 的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：\(x_1=x_2,x_2=x_3,x_3=x_4,x_4\neq x_1\)，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

输入格式

输入的第一行包含一个正整数 \(t\)，表示需要判定的问题个数。注意这些问题之间是相互独立的。

对于每个问题，包含若干行：

第一行包含一个正整数 \(n\)，表示该问题中需要被满足的约束条件个数。接下来 \(n\) 行，每行包括三个整数 \(i,j,e\)，描述一个相等/不等的约束条件，相邻整数之间用单个空格隔开。若 \(e=1\)，则该约束条件为 \(x_i=x_j\)。若\(e=0\)，则该约束条件为 \(x_i\neq x_j\)。

输出格式

输出包括 \(t\) 行。

输出文件的第 \(k\) 行输出一个字符串 YES 或者 NO（字母全部大写），YES 表示输入中的第 \(k\) 个问题判定为可以被满足，NO 表示不可被满足。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
2
2
1 2 1
1 2 0
2
1 2 1
2 1 1

样例输出 #1

1
2
NO
YES

样例 #2

样例输入 #2

1
2
3
4
5
6
7
8
9
10
2
3
1 2 1
2 3 1
3 1 1
4
1 2 1
2 3 1
3 4 1
1 4 0

样例输出 #2

1
2
YES
NO

提示

【样例解释1】

在第一个问题中，约束条件为：\(x_1=x_2,x_1\neq x_2\)。这两个约束条件互相矛盾，因此不可被同时满足。

在第二个问题中，约束条件为：\(x_1=x_2,x_1 = x_2\)。这两个约束条件是等价的，可以被同时满足。

【样例说明2】

在第一个问题中，约束条件有三个：\(x_1=x_2,x_2= x_3,x_3=x_1\)。只需赋值使得 \(x_1=x_2=x_3\)，即可同时满足所有的约束条件。

在第二个问题中，约束条件有四个：\(x_1=x_2,x_2= x_3,x_3=x_4,x_4\neq x_1\)。由前三个约束条件可以推出 \(x_1=x_2=x_3=x_4\)，然而最后一个约束条件却要求 \(x_1\neq x_4\)，因此不可被满足。

【数据范围】

所有测试数据的范围和特点如下表所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
//P1955[NOI2015] 程序自动分析
//本题考查并查集和离散化
/*
把所有e==1的操作放在前面，然后再进行e==0的操作，在进行e==1的操作的时候，我们只要把它约束的两个变量放在同一个集合里面即可。在e==0，即存在一条不相等的约束条件，对于它约束的两个变量，如果在一个集合里面，那就不可能满足！如不相等的约束条件都满足，那就YES。
*/
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define frep(i, a, n) for (int i = a; i >= n; i--)
const int N=1e6;
struct node{
    int x,y,z;
}a[N];
int b[N];
int c[N];
int fa[N];
int find(int x)
{
    if(fa[x]==x)
    {
        return x;
    }
    return fa[x]=find(fa[x]);
}
void merge(int x,int y)
{
    x=find(x);
    y=find(y);
    if(x!=y)
{
    fa[x]=y;
}
}
int n;
int main()
{
int t;
cin>>t;
while(t--)
{
    cin>>n;
    int btop=0;
    int ctop=0;
    rep(i,1,n)
{
    cin>>a[i].x>>a[i].y>>a[i].z;
    b[++btop]=a[i].x;
    b[++btop]=a[i].y;
}
sort(b+1,b+1+btop);
rep(i,1,btop)
{
    if(b[i]!=b[i-1]||i==1)
    {
        c[++ctop]=b[i];
    }
}
rep(i,1,n)
{
    a[i].x=lower_bound(c+1,c+1+ctop,a[i].x)-c;
    a[i].y=lower_bound(c+1,c+1+ctop,a[i].y)-c;
}
    //以上都是离散化
rep(i,1,ctop)
{
    fa[i]=i;
}
rep(i,1,n)
{
    if(a[i].z)
    {
        merge(a[i].x,a[i].y);
    }
}
bool mk=1;
rep(i,1,n)
{
    if(!a[i].z)
    {
        if(find(a[i].x)==find(a[i].y))
        {
            mk=0;
        }
    }
}
    //并查集部分
    //先真再看假的部分能不能反驳真
if(mk)
{
    cout<<"YES"<<'\n';
}
else
{
    cout<<"NO"<<'\n';
}

}
return 0;

}

[JLOI2011] 不重复数字

题目描述

给定 \(n\) 个数，要求把其中重复的去掉，只保留第一次出现的数。

输入格式

本题有多组数据。

第一行一个整数 \(T\)，表示数据组数。

对于每组数据：

第一行一个整数 \(n\)。

第二行 \(n\) 个数，表示给定的数。

输出格式

对于每组数据，输出一行，为去重后剩下的数，两个数之间用一个空格隔开。

样例 #1

样例输入 #1

1
2
3
4
5
2
11
1 2 18 3 3 19 2 3 6 5 4
6
1 2 3 4 5 6

样例输出 #1

1
2
1 2 18 3 19 6 5 4
1 2 3 4 5 6

提示

对于 \(30\%\) 的数据，\(n \le 100\)，给出的数 \(\in [0, 100]\)。

对于 \(60\%\) 的数据，\(n \le 10^4\)，给出的数 \(\in [0, 10^4]\)。

对于 \(100\%\) 的数据，\(1 \le T\le 50\)，\(1 \le n \le 5 \times 10^4\)，给出的数在 \(32\) 位有符号整数范围内。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<bits/stdc++.h>
using namespace std;
struct node{
	int val;
	int id;
		inline bool operator <(const node &rhs)const {
		return val<rhs.val||val==rhs.val&&id<rhs.id;
	}
	inline bool operator ==(const node &rhs)const {
		return val==rhs.val;
	}
    //unique的必须判定
}a[1000000];
bool cmp(node x,node y)
{
	return x.id<y.id;
}
//按照顺序排序，满足题意
int main()
{
	int t;
	cin>>t;
	while(t--)
	{
		int n;
		cin>>n;
		
		for(int i=1;i<=n;i++)
		{
			cin>>a[i].val;
			a[i].id=i;	
		}
		sort(a+1,a+1+n);
		int x=unique(a+1,a+1+n)-1-a;
		sort(a+1,a+1+x,cmp);
		for(int i=1;i<=x;i++)
		{
			cout<<a[i].val<<" ";
		}
		
		cout<<'\n';
	}	
}

[TJOI2010] 阅读理解

题目描述

英语老师留了 \(N\) 篇阅读理解作业，但是每篇英文短文都有很多生词需要查字典，为了节约时间，现在要做个统计，算一算某些生词都在哪几篇短文中出现过。

输入格式

第一行为整数 \(N\) ，表示短文篇数，其中每篇短文只含空格和小写字母。

按下来的 \(N\) 行，每行描述一篇短文。每行的开头是一个整数 \(L\) ，表示这篇短文由 \(L\) 个单词组成。接下来是 \(L\) 个单词，单词之间用一个空格分隔。

然后为一个整数 \(M\) ，表示要做几次询问。后面有 \(M\) 行，每行表示一个要统计的生词。

输出格式

对于每个生词输出一行，统计其在哪几篇短文中出现过，并按从小到大输出短文的序号，序号不应有重复，序号之间用一个空格隔开（注意第一个序号的前面和最后一个序号的后面不应有空格）。如果该单词一直没出现过，则输出一个空行。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
10
3
9 you are a good boy ha ha o yeah
13 o my god you like bleach naruto one piece and so do i
11 but i do not think you will get all the points
5
you
i
o
all
naruto

样例输出 #1

1
2
3
4
5
1 2 3
2 3
1 2
3
2

提示

对于 \(30\%\) 的数据， \(1\le M\le 10^3\) 。

对于 \(100\%\) 的数据，\(1\le M\le 10^4\)，\(1\le N\le 10^3\) 。

每篇短文长度（含相邻单词之间的空格）\(\le 5\times 10^3\) 字符，每个单词长度 \(\le 20\) 字符。

每个测试点时限 \(2\) 秒。

感谢@钟梓俊添加的一组数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<bits/stdc++.h>
using namespace std;
const int N = 1000010;
int n, m, num, cnt[N];
string s;
map<string,vector<int> >a;
int main()
{	
	cin>>n;
	for(int i = 1; i <= n; i++)
	{
		cin>>num;
		for(int j = 1; j <= num; j++)
		{
			cin>>s;
			a[s].push_back(i);
		}
	}
	cin>>m;
	for(int i = 1; i <= m; i++)
	{
		cin>>s;
		memset(cnt,0,sizeof(cnt));
		for(int j = 0; j < a[s].size(); j++)
		if(cnt[a[s][j]] == 0)
		{
			cout<<a[s][j]<<" ";
			cnt[a[s][j]]++;
            //去重的桶
		}
		cout<<'\n';
	}
}

家谱

题目背景

现代的人对于本家族血统越来越感兴趣。

题目描述

给出充足的父子关系，请你编写程序找到某个人的最早的祖先。

输入格式

输入由多行组成，首先是一系列有关父子关系的描述，其中每一组父子关系中父亲只有一行，儿子可能有若干行，用 #name 的形式描写一组父子关系中的父亲的名字，用 +name 的形式描写一组父子关系中的儿子的名字；接下来用 ?name 的形式表示要求该人的最早的祖先；最后用单独的一个 $ 表示文件结束。

输出格式

按照输入文件的要求顺序，求出每一个要找祖先的人的祖先，格式为：本人的名字 \(+\) 一个空格 \(+\) 祖先的名字 \(+\) 回车。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
10
11
12
#George
+Rodney
#Arthur
+Gareth
+Walter
#Gareth
+Edward
?Edward
?Walter
?Rodney
?Arthur
$

样例输出 #1

1
2
3
4
Edward Arthur
Walter Arthur
Rodney George
Arthur Arthur

提示

规定每个人的名字都有且只有 \(6\) 个字符，而且首字母大写，且没有任意两个人的名字相同。最多可能有 \(10^3\) 组父子关系，总人数最多可能达到 \(5 \times 10^4\) 人，家谱中的记载不超过 \(30\) 代。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<iostream>
#include<map>
using namespace std;
map<string,string>p;
string find(string x)
{
    if(x!=p[x]) 
        p[x]=find(p[x]);
    return  p[x];
}
//类似于不断查祖先罢
string s,s1;
int main()
{
    char ch;
    cin>>ch;
    while(ch!='')
    {
        cin>>s;
        if(ch=='#')
        {
            s1=s;
            if(p[s]=="") p[s]=s;
        }
        else if(ch=='+')
            p[s]=s1;
        else 
            cout<<s<<' '<<find(s)<<'\n';    
        cin>>ch;
    }

}