KMP

KMP算法——通俗易懂讲好KMP算法：实例图解分析+详细代码注解 --》你的所有疑惑在本文都能得到解答_kmp算法例子-CSDN博客

"字符串A是否为字符串B的子串?如果是的话出现在B的哪些位置?"该问题就是字符串匹配问题，字符串A称为模式串，字符串B称为主串。

暴力算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 暴力匹配
int i = 0, j = 0;
while (i < s.length())
{
    if (s[i] == p[j])
        ++i, ++j;
    else
        i = i - j + 1, j = 0;
    if (j == p.length())  // 匹配成功
    {
        // 对s[i - j .. i - 1]进行一些操作
        cout << i - j << endl;
        i = i - j + 1;
        j = 0;
    }
}

KMP 方法算法就利用之前判断过的信息，通过一个 next 数组，保存模式串中前后最长公共子序列的长度，每次回溯时，通过 next 数组找到，前面匹配过的位置，省去了大量的计算时间。

所以：

前置知识

字符串的前缀

是指不包含最后一个字符的所有以第一个字符（索引为0）开头的连续子串

比如字符串 “ABABA” 的前缀有：A，AB，ABA，ABAB

字符串的后缀

是指不包含第一个字符的所有以最后一个字符结尾的连续子串

比如字符串 “ABABA” 的后缀有：BABA，ABA，BA，A

公共前后缀：

一个字符串的 所有前缀连续子串 和 所有后缀连续子串 中相等的子串

上述字符串则是：A ，ABA

最长公共前后缀：

所有公共前后缀 的 长度最长的 那个子串：ABA

举例：ABCA的最长公共前后缀 为 1

ABCAB的最长公共前后缀 为 2

Next表的构建

子串 “A”：最后一个字符是 A，该子串的最长公共前后缀长度是 0，因此对应关系就是 A - 0 子串 “AB”：最后一个字符是 B，该子串的最长公共前后缀长度是 0，因此对应关系就是 B - 0 子串 “ABC”：最后一个字符是 C，该子串的最长公共前后缀长度是 0，因此对应关系就是 C - 0 子串 “ABCA”：最后一个字符是 A，该子串的最长公共前后缀长度是 1，因此对应关系就是 A - 1 子串 “ABCAB”：最后一个字符是 B，该子串的最长公共前后缀长度是 2，因此对应关系就是 B - 2 子串 “ABCABD”：最后一个字符是 D，该子串的最长公共前后缀长度是 0，因此对应关系就是 D - 0 则得到表next = [0, 0, 0, 1, 2, 0]

简单地说，next[i]就是，从a[0]往后数、同时从a[i]往前数相同的位数，在保证前后缀相同的情况下，最多能数多少位。

它是真前缀与真后缀的集合之交集中，最长元素的长度。

深入解释一下

1
2
3
4
5
6
7
8
9
10
11
//有两个字符串
abababcabaa
ababcabaa
//一开始进行匹配
//匹配到
ababa
ababc
//时候出现问题
//这时候如果是暴力，已经i移动到第二位，j回到0开始匹配了
//但kmp有next啊，我们可以看前面4个字母的最长公共前后缀，就是2
//于是j回到2，也就是a的位置，继续与c匹配，这就是回跳，令j=next[j-1](保证正确性)

转换为代码，这是主串与模式串的匹配

其中p是要匹配的短串，s是被匹配的长串

1
2
3
4
5
6
7
8
9
10
for (int i = 0, j = 0; i < s.length(); ++i)
{
    while (j && s[i] != p[j]) j = pmt[j - 1]; // 不断前移j指针，直到成功匹配或移到头为止
    if (s[i] == p[j]) j++;  // 当前位匹配成功，j指针右移
    if (j == p.length())
    {
        // 对s[i - j + 1 .. i]进行一些操作
        j = pmt[j - 1];
    }
}

自己与自己匹配，得到pmi数组

1
2
3
4
5
6
7
8
9
// pmt[0] = 0;
//由于p串第一位的pmt肯定是0，所以我们把他移动一位，进行匹配，就可以求解出
//就是在错开一位后，让p自己匹配自己（这相当于是用前缀去匹配后缀）。
for (int i = 1, j = 0; i < plen; ++i)
{
    while (j && p[i] != p[j]) j = pmt[j - 1];
    if (p[i] == p[j]) j++;
    pmt[i] = j;
}

【模板】KMP

题目描述

给出两个字符串 \(s_1\) 和 \(s_2\)，若 \(s_1\) 的区间 \([l, r]\) 子串与 \(s_2\) 完全相同，则称 \(s_2\) 在 \(s_1\) 中出现了，其出现位置为 \(l\)。
现在请你求出 \(s_2\) 在 \(s_1\) 中所有出现的位置。

定义一个字符串 \(s\) 的 border 为 \(s\) 的一个非 \(s\) 本身的子串 \(t\)，满足 \(t\) 既是 \(s\) 的前缀，又是 \(s\) 的后缀。
对于 \(s_2\)，你还需要求出对于其每个前缀 \(s'\) 的最长 border \(t'\) 的长度。

输入格式

第一行为一个字符串，即为 \(s_1\)。
第二行为一个字符串，即为 \(s_2\)。

输出格式

首先输出若干行，每行一个整数，按从小到大的顺序输出 \(s_2\) 在 \(s_1\) 中出现的位置。
最后一行输出 \(|s_2|\) 个整数，第 \(i\) 个整数表示 \(s_2\) 的长度为 \(i\) 的前缀的最长 border 长度。

样例 #1

样例输入 #1

1
2
ABABABC
ABA

样例输出 #1

1
2
3
1
3
0 0 1

提示

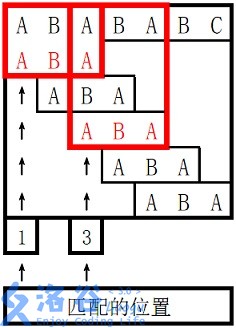
样例 1 解释

对于 \(s_2\) 长度为 \(3\) 的前缀 ABA，字符串 A 既是其后缀也是其前缀，且是最长的，因此最长 border 长度为 \(1\)。

数据规模与约定

本题采用多测试点捆绑测试，共有 3 个子任务。

  • Subtask 1（30 points）：\(|s_1| \leq 15\)，\(|s_2| \leq 5\)。
  • Subtask 2（40 points）：\(|s_1| \leq 10^4\)，\(|s_2| \leq 10^2\)。
  • Subtask 3（30 points）：无特殊约定。

对于全部的测试点，保证 \(1 \leq |s_1|,|s_2| \leq 10^6\)，\(s_1, s_2\) 中均只含大写英文字母。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<bits/stdc++.h>
const int  N= 1000010;
using namespace std;
int kmp[N];
int la,lb,j; 
string a;
string b;
int main()
{
    cin>>a;
    cin>>b;
    a=" "+a;
    b=" "+b;
    la=a.length()-1;
    lb=b.length()-1;
    for (int i=2;i<=lb;i++)
	   {     
	   while(j&&b[i]!=b[j+1])
        j=kmp[j];    
       if(b[j+1]==b[i])j++;    
        kmp[i]=j;
       }
    j=0;
    for(int i=1;i<=la;i++)
	   {
          while(j>0&&b[j+1]!=a[i])
           j=kmp[j];
          if (b[j+1]==a[i]) 
           j++;
          if (j==lb) 
		  {
		  cout<<i-lb+1<<'\n';
		  j=kmp[j];
		  }
       }

    for (int i=1;i<=lb;i++)
    cout<<kmp[i]<<" ";

}