SCUT数据结构2008年考试
SCUT数据结构2008年考试
选择题
(1) 算法必须满足以下所有条件,除了:
- 正确 (B) 有限 (C) 模糊 (D) 具体步骤
答案:C
解释: 一个算法应该是正确的(给出正确的结果)、有限的(在有限时间内完成)、并且具有具体步骤(清晰的执行过程)。然而,算法不应该是模糊的,模糊性会导致不确定性和错误。
(2) 选择对应于当 $ n $ 增大时最有效算法的增长率:
- $ 2n^3 $ (B) $ 2^n $ (C) $ n! $ (D) $ 20n^2 n $
答案:D
解释: 当 $ n $ 较大时, $ n! $ 增长速度最快,接下来是 $ 2n^3 $,而 $ 20n^2 n $ 的增长率则相对较慢。在给定选项中,$ 20n^2 n $ 是最有效率的,因为其增长速度比 $ n! $ 和 $ 2n^3 $ 要慢,适用于大规模数据。
(3) 如果一个数据元素需要 8 字节,而一个指针需要 2 字节,则当非空元素的比例低于以下值时,链表表示会比标准数组表示更节省空间:
- $ $ (B) $ $ (C) $ $ (D) $ $
答案:B
解释: 在数组中,每个元素都占用 8 字节,而在链表中,每个非空元素需要 8 字节和 2 字节的指针,总共 10 字节。因此,当非空元素的比例低于 $ $ 时,链表表示比数组更有效。
(4) 以下四个陈述中哪一个是不正确的:
- 堆排序是一种不稳定的排序算法。
- 簇是文件分配的最小单元,因此所有文件都占用簇大小的整数倍。
- 我算法的最坏情况是 $ n $ 变得越来越大,因为那是最慢的。
- 在非空二叉树中,空子树的数量比树中的节点数量多一个。
答案:B
解释: 堆排序确实是不稳定的,空子树的数量等于节点数加一。在文件系统中,簇是文件分配的最小单元,因此所有文件的大小通常是簇大小的整数倍。选项B是不正确的,因为并不是所有文件都一定会占用完整的簇大小,尤其是在文件大小小于一个簇时。
(5) 以下哪项是正确的陈述:
- 一般树可以转换为具有左子节点和右子节点的二叉树。
- 在二叉搜索树中,可以通过前序遍历对节点进行排序。
- 在二叉搜索树中,任何节点的左子节点小于右子节点,但在堆中,任何节点的左子节点可以小于或大于右子节点。
- 堆的形状类似于完全二叉树。
答案:C
解释: 一般树不能简单地转换为具有左右子节点的二叉树,前序遍历不能用于对二叉搜索树进行排序。在二叉搜索树中,左子节点总是小于右子节点,而在堆中,左右子节点的值没有严格的大小关系。选项C正确描述了这两种数据结构的特性。D应该不能够说成是类似,就是完全二叉树的结构。
(6) 减少基于磁盘的程序所需时间的最有效方法是:
(A) 改善基本操作。
(B) 最小化磁盘访问次数。
(C) 消除递归调用。
(D) 减少主存使用。
答案:B
解释:
磁盘访问是程序性能的主要瓶颈之一。最小化磁盘访问次数可以显著提高程序效率,因为每次访问磁盘都会消耗大量时间。通过有效利用缓存和优化数据结构,可以减少对磁盘的访问,从而加快程序运行速度。
(7) 通过键序列 (54, 32, 45, 63, 76, 84) 构造的最大堆是:
(A) 84, 63, 54, 76, 32, 45
(B) 84, 76, 45, 63, 54, 32
(C) 84, 63, 76, 32, 45, 54
(D) 84, 76, 54, 63, 32, 45
答案:D
解释:
在最大堆中,父节点的值总是大于或等于其子节点的值。构造最大堆时,首先将所有元素插入,然后调整结构以满足最大堆性质。根据给定的键序列,最终得到的最大堆为
84(根节点),76(左子节点),54(右子节点),63,32 和 45。
(8) 如果工作内存为1MB,块大小为8KB,则工作内存可以容纳128个块。通过外部排序中的多路归并,平均运行大小和在一次多路归并中的排序大小分别是:
(A) 1MB, 128 MB
(B) 2MB, 512MB
(C) 2MB, 256 MB
(D) 1MB, 256MB
答案:C
解释:
在多路归并过程中,平均运行大小通常是工作内存的两倍(即
2MB),而在一次多路归并中可以排序的大小是工作内存和块数的乘积,这里为
256MB。这个计算的基础是:每个块可以在一次归并中处理。
(9) 树索引方法旨在克服哈希中的什么缺陷?
(A) 无法处理范围查询。
(B) 无法处理最大查询。
(C) 无法按键顺序处理查询。
(D) 以上全部。
答案:D
解释:
哈希表在处理特定类型的查询时存在局限性,如范围查询和有序查询等。树索引能够支持这些操作,因此树索引方法被用来克服哈希表的这些缺陷。
(10) 假设我们有八个记录,键值从 A 到 H,并且它们最初按字母顺序放置。现在,考虑应用以下访问模式:F D F G E G F A D F G E,如果使用前移启发式组织列表,则最终列表将是:
(A) E G F D A C H B
(B) E G F D A B C H
(C) F D G A E C B H
(D) F D G E A B C H
答案:B
解释:
前移启发式策略的基本思路是,当访问某个元素时,将其移动到列表的最前面。根据给定的访问模式,元素
F、D、G 和 E 被多次访问,因此它们会不断向前移动,最终形成新的顺序:E G F
D A B C H。
填空题
(1) 给定一个按值排序的整数数组,修改二分查找例程以返回第一个值大于 K 的整数的位置,当 K 本身不出现在数组中时。如果数组中的最小值大于 K,则返回 ERROR。
代码如下:
1 | // 返回最大值 <= K 的元素位置 |
解释:
- 这个
newbinary函数使用二分查找算法来寻找数组中第一个大于 K 的整数的索引。 - 初始化
l为 -1 和r为数组长度n,这使得l和r超出数组的边界。 - 在循环中,计算中间索引
i,并通过与 K 比较来调整l和r的值:- 如果 K 小于
array[i],则搜索范围缩小到左半部分,将r设置为i。 - 如果 K 等于
array[i],返回当前索引i。 - 如果 K 大于
array[i],则在右半部分继续搜索,将l设置为i。
- 如果 K 小于
- 最后,如果 K 大于数组的最小值(
array[0])或l不等于 -1(表示存在小于 K 的元素),则返回l。否则返回 ERROR,表示数组中的最小值大于 K。
(2) 一个拥有 100 个内部顶点的完全 6-叉树有多少个顶点?
答案:601
解释:
在一个完全 $ k $-叉树中,若有 $ I $ 个内部顶点,则树中总顶点数 $ N $ 可以用以下公式计算:
$ N = I + (k-1) I + 1 $
这里,$ I $ 是内部顶点的数量,$ k $ 是每个内部节点的孩子数量。在这个例子中:
- $ I = 100 $
- $ k = 6 $
将这些值代入公式中:
$ N = 100 + (6 - 1) + 1 = 100 + 500 + 1 = 601 $
因此,完全 6-叉树的总顶点数为 601。
给定某个二叉树的前序遍历和中序遍历,绘制该二叉树并给出后序遍历。
前序遍历: ABECDFGHIJ 中序遍历: EBCDAFHIGJ

Postorder enumeration: EDCBIHJGFA
题目:代码复杂度分析
代码片段 1:
1 | sum = 0; |
- 外层循环从
i = 0到i < 3,总共执行 3次。 - 内层循环从
j = 0到j < n,每次执行n次操作。
总的操作次数为:
$ 3 n = 3n $ 忽略常数系数,时间复杂度为 Θ(n)。
答案: Θ(n)
代码片段 2:
1 | sum = 0; |
- 外层循环从
i = 1到i = n,总共执行 n次。 - 内层循环对于每个
i,执行i次操作。
总的操作次数为:
$ 1 + 2 + 3 + + n = $ 忽略常数系数,时间复杂度为
Θ(n^2)。
答案: Θ(n²)
代码片段 3:
1 | sum = 0; |
- 如果
n是偶数,for循环将执行 n次,总操作次数为 n。 - 如果
n是奇数,则只进行一次加法操作,时间复杂度为 常数时间(Θ(1))。
但在平均情况下,无论 n
是偶数还是奇数,主导操作是 n 的循环操作,因此时间复杂度是
Θ(n)。
答案: Θ(n)
总结:
- 代码片段 1:Θ(n)
- 代码片段 2:Θ(n²)
- 代码片段 3:Θ(n)
这三个代码片段的时间复杂度分析依据循环结构和分支条件推导而来,忽略常数系数和非主导项。
题目:
使用闭合哈希和双重哈希来解决碰撞,将以下键插入一个有11个插槽(编号从0到10)的哈希表中。使用的哈希函数H1和H2如下所示。请在插入所有八个键后显示哈希表,并清楚说明如何使用H1和H2进行哈希。
哈希函数:
- $ H1(k) = 3k $
- $ H2(k) = 7k + 1 $
键:22, 41, 53, 46, 30, 13, 1, 67。(8分)
解答过程:
步骤 1: 插入键 22
- 计算 $ H1(22) \(:\) H1(22) = 3 = 66 = 0 $
- 插入到位置 0:
- 哈希表:
[22, -, -, -, -, -, -, -, -, -, -]
- 哈希表:
步骤 2: 插入键 41
- 计算 $ H1(41) \(:\) H1(41) = 3 = 123 = 2 $
- 插入到位置 2:
- 哈希表:
[22, -, 41, -, -, -, -, -, -, -, -]
- 哈希表:
步骤 3: 插入键 53
- 计算 $ H1(53) \(:\) H1(53) = 3 = 159 = 5 $
- 插入到位置 5:
- 哈希表:
[22, -, 41, -, -, 53, -, -, -, -, -]
- 哈希表:
步骤 4: 插入键 46
- 计算 $ H1(46) \(:\) H1(46) = 3 = 138 = 6 $
- 插入到位置 6:
- 哈希表:
[22, -, 41, -, -, 53, 46, -, -, -, -]
- 哈希表:
步骤 5: 插入键 30
- 计算 $ H1(30) \(:\) H1(30) = 3 = 90 = 2 $
- 位置 2 已经被 41 占用,因此需要使用 $ H2(30) $ 来寻找新的位置: $ H2(30) = 7 + 1 = 210 + 1 = 0 + 1 = 1 $
- 使用 $ H2(30) $ 计算新的位置: $ = (H1(30) + i H2(30)) (i = 1, 2, ) $ $ i = 1: (2 + 1 ) = 3 (位置 3 空) $
- 插入到位置 3:
- 哈希表:
[22, -, 41, 30, -, 53, 46, -, -, -, -]
- 哈希表:
步骤 6: 插入键 13
- 计算 $ H1(13) \(:\) H1(13) = 3 = 39 = 6 $
- 位置 6 已经被 46 占用,因此需要使用 $ H2(13) \(:\) H2(13) = 7 + 1 = 91 + 1 = 1 + 1 = 2 $
- 使用 $ H2(13) $ 计算新的位置: $ i = 1: (6 + 1 ) = 8 (位置 8 空) $
- 插入到位置 8:
- 哈希表:
[22, -, 41, 30, -, 53, 46, -, 13, -, -]
- 哈希表:
步骤 7: 插入键 1
- 计算 $ H1(1) \(:\) H1(1) = 3 = 3 $
- 位置 3 已经被 30 占用,因此需要使用 $ H2(1) \(:\) H2(1) = 7 + 1 = 7 + 1 = 7 + 1 = 8 $
- 使用 $ H2(1) $ 计算新的位置: $ i = 1: (3 + 1 ) = 11 = 0 (位置 0 已占) $ $ i = 2: (3 + 2 ) = 19 = 8 (位置 8 已占) $ $ i = 3: (3 + 3 ) = 27 = 5 (位置 5 已占) $ $ i = 4: (3 + 4 ) = 35 = 2 (位置 2 已占) $ $ i = 5: (3 + 5 ) = 43 = 9 (位置 9 空) $
- 插入到位置 9:
- 哈希表:
[22, -, 41, 30, -, 53, 46, -, 13, 1, -]
- 哈希表:
步骤 8: 插入键 67
- 计算 $ H1(67) \(:\) H1(67) = 3 = 201 = 3 $
- 位置 3 已经被 30 占用,因此需要使用 $ H2(67) \(:\) H2(67) = 7 + 1 = 469 + 1 = 9 + 1 = 10 $
- 使用 $ H2(67) $ 计算新的位置: $ i = 1: (3 + 1 ) = 13 = 2 (位置 2 已占) $ $ i = 2: (3 + 2 ) = 23 = 1 (位置 1 空) $
- 插入到位置 1:
- 哈希表:
[22, 67, 41, 30, -, 53, 46, -, 13, 1, -]
- 哈希表:
最终哈希表:
1 | [22, 67, 41, 30, -, 53, 46, -, 13, 1, -] |
结果:
- 哈希表经过插入操作后如下所示:
- 位置 0: 22
- 位置 1: 67
- 位置 2: 41
- 位置 3: 30
- 位置 4: -
- 位置 5: 53
- 位置 6: 46
- 位置 7: -
- 位置 8: 13
- 位置 9: 1
- 位置 10: -
- 所有键都已成功插入哈希表,碰撞已通过双重哈希解决。
题目:
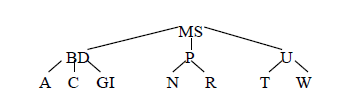
给定一系列整数键的记录,记录按以下顺序到达:C, S, D, T, A, M, P, I, B, W, N, G, U, R。请展示插入这些记录后得到的2-3树。并要求展示解决过程。(7分)
答案:
题目:
答案 1. 使用 Dijkstra 算法找出从顶点 C 到所有其他顶点的最短路径。(4分) 2. 使用 Kruskal 算法找出最小生成树。(3分) 3. 展示从顶点 A 开始的深度优先搜索树。(3分)