lec4 Trees(3)

image-20241119170227426AVL树已经彻底掌握了！欢迎来到还没掌握完全的Splay，之后的数据结构内容都很简单，很快就可以解决。

Splay Trees

自调整树 (Self-Adjusting Trees)

  1. 普通二叉搜索树没有平衡条件
    • 普通的二叉搜索树（BST）没有强制要求树的平衡。它的结构完全依赖于插入顺序。如果插入顺序不理想，树可能会退化为链表结构，导致操作性能低下。
  2. 平衡树（如AVL树）通过强制平衡条件来确保树在节点变化时始终保持平衡
    • 平衡树（如AVL树）在每次插入或删除时会调整树的结构，确保树的高度平衡，使得查找、插入和删除操作的时间复杂度维持在对数级别。
  3. 自调整树随着节点的访问而重新组织
    • 自调整树的特点是，在节点被访问时，树会根据访问的顺序进行自我调整。这样做的目的是在一段时间内保持树的局部平衡，而不是始终强制保持完全平衡。
    • 树的结构会根据访问顺序不断调整，以使得访问频繁的节点靠近树的根部，从而提高后续访问的效率。
  4. 自调整树的调整方式
    • 自调整树通过插入、删除或查找操作来进行调整。这种调整方式使得树根据节点的访问模式逐步趋于更合理的结构。
    • 例如，访问某个节点时，通过一系列的旋转操作将该节点调整到树的根部。

Splay树简介

  1. Splay树并不是一个完全平衡的树
    • Splay树是一种自调整二叉搜索树，它在每次节点访问后进行“splaying”操作，将访问的节点移动到树的根部。这种树并不总是保持完美的平衡，而是根据访问模式动态调整。
  2. Splay树的特点：
    • 最近访问的数据会靠近树的根部。
    • 这遵循局部性原理（Locality Principle），即最近访问的数据会在未来的操作中被再次访问，因此将其靠近根部可以提高未来操作的效率。
    • 这种机制也与80-20规则相符，即80%的访问集中在20%的节点上，Splay树通过将常访问的节点移动到树的根部，利用这一规律提高查找效率。
  3. Splaying操作
    • 当访问到节点X时，Splay树会执行一系列的旋转操作，确保X节点最终成为树的根节点。通过这些旋转操作，树的结构会被调整，使得树的整体平衡性得到改善。
  4. Splay树的调整方式：
    • Splay树不是在每次插入或删除时自动调整，而是在每次查找操作后对树进行调整。这样，树在后续操作中可能会变得更加平衡，有助于提高查找效率。
  5. Splay树的优缺点：
    • 优点：
      • 在频繁访问某些节点时，Splay树能够通过自调整机制有效提高这些节点的访问速度。
      • 它不需要额外的存储空间来维护平衡因子，因此节省了空间开销。
    • 缺点：
      • Splay树在插入和删除操作时可能会产生较大的树结构变化，导致某些情况下的操作时间较慢。
      • 由于它不是总保持平衡，极端情况下可能会退化为链表结构，导致操作效率下降。

怎么进行Splaying

基本思路

  • 单旋转：在执行Splaying时，可以从底部到顶部进行单旋转操作，逐步将目标节点调整到树的根部。
  • 底部到顶部的策略：这种策略虽然简单，但可能不够高效，特别是在多次操作后，性能不如预期。

性能分析

  • 问题：单个操作的时间复杂度为O(n)，这是因为每次旋转都会向树的上方逐步推进，可能涉及多个节点的调整。
  • 旋转的总数：对于N个节点的树，插入键（N, N-1, ..., 1）时，旋转次数的总和为： $ (n - 1) + (n - 2) + ... + 1 = O(n^2) $ 这意味着每个操作可能需要O(n)的时间，尤其是在最坏情况下，整个序列的操作总共可能需要Ω(n²)的时间。

目标

  • 局部性原理（Principle of Locality）：通过让最常访问的节点靠近树的根部，可以提高后续操作的效率。Splay树的设计目标之一是利用这一原理，确保常访问的节点总是快速可达。
  • 每次操作的摊销时间：Splay树的目标是使得每次操作的摊销时间达到O(log N)，即使某些操作可能需要较长时间，但通过多次操作平均分摊后，整体时间复杂度依然保持在对数级别。

如何执行 Splaying 操作？

除了使用单旋转进行调整外，双旋转（Double Rotation）策略也被用于优化Splaying操作。

术语说明

在Splay树中，我们定义了一些重要的术语和操作：

  • X：一个非根节点，它有两个或更多的祖先节点。
  • P：X的父节点。
  • G：X的祖父节点。

旋转类型

在执行Splay操作时，我们需要使用不同的旋转方式，这些旋转有助于将节点X移到树的根部。旋转的类型有：

  1. Zig-Zig（字形旋转）：
    • 描述：当父节点和祖父节点在同一方向时，我们执行Zig-Zig旋转。
    • 操作：如果父节点和祖父节点都位于树的左侧或者都位于右侧时，就执行一次Zig-Zig旋转。
  2. Zig-Zag（之字形旋转）：
    • 描述：当父节点和祖父节点在不同方向时，我们执行Zig-Zag旋转。
    • 操作：如果父节点在树的左侧而祖父节点在树的右侧，或者反之，就执行一次Zig-Zag旋转。

Splay树操作：

需要的条件：

  • 父节点指针：如果节点包含指向父节点的指针，Splay操作会更容易实现。

旋转操作：

当访问节点X时，我们根据X的父节点P和祖父节点G的关系，选择适当的旋转类型。Splay操作分为单旋转和双旋转。

单旋转（Single Rotations）

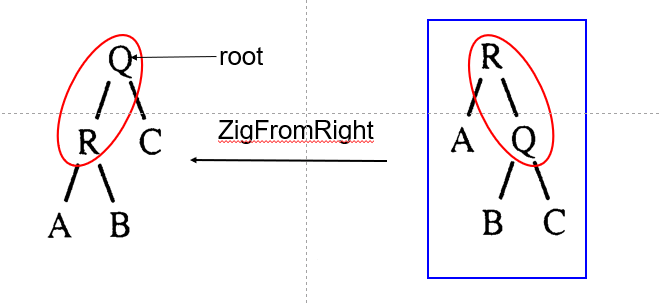
如果X有一个父节点P，但没有祖父节点G，则执行单旋转操作。此时，我们有两种旋转操作：

  • ZigFromLeft：如果P是X的左孩子，执行单旋转。
image-20241119195045785
  • ZigFromRight：如果P是X的右孩子，执行单旋转。
image-20241119195101743

双旋转（Double Rotations）

如果X有父节点P且祖父节点G，则执行双旋转操作。根据父节点和祖父节点的关系，选择合适的旋转类型。双旋转有以下六种情况：

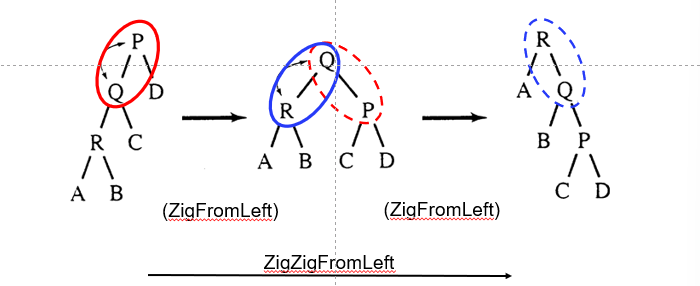
  1. ZigZigFromLeft：当父节点和祖父节点都在左边时，执行一次双旋转。
  2. ZigZigFromRight：当父节点和祖父节点都在右边时，执行一次双旋转。
  3. ZigZagFromLeft：当父节点在左边，祖父节点在右边时，执行一次双旋转。
  4. ZigZagFromRight：当父节点在右边，祖父节点在左边时，执行一次双旋转。

图示：

image-20241119195219158image-20241119195335096

image-20241119195800548

总结一下：如果在同一个方向，就先旋转父节点，后旋转子节点。

如果不在同一个方向，就按照AVL树的方法正常旋转。

注意一定要旋转到根节点。

Splay树的插入与删除操作

插入操作 (Insert x)

  1. 插入 x：按照普通的二叉搜索树（BST）插入方法将元素x插入到树中。
  2. Splay x：插入完成后，将节点x通过Splay操作移动到树的根部。

删除操作 (Delete x)

  1. Splay x：首先，通过Splay操作将要删除的节点x移动到树的根部。
  2. 删除节点：从树中移除节点x。此时，删除节点不需要像二叉搜索树那样是叶子节点或只有一个子节点。
  3. 处理两个子树：删除后，树会分为两个部分——x的左子树和右子树。
  4. Splay最大节点到根：接下来，将x的左子树中的最大节点通过Splay操作移动到根部。
  5. 合并子树：将原右子树附加到新的根节点（即原左子树中的最大节点）的右子树上。
image-20241119200409037

插入顺序为1, 2, 3, ..., 8的情况

  • 没有自调整的情况：如果插入顺序是1, 2, 3, ..., 8，并且没有进行自调整（即没有Splay操作），那么插入n个元素的时间复杂度是O(n²)，因为每次插入都需要遍历树的高度（对于递增的顺序，树会退化成链表）。

  • 使用自调整（Splay）操作的情况：如果使用Splay操作，那么每次插入的时间复杂度是O(1)，因此n个插入的总时间复杂度为O(n)。

Splay树的优势

  • 平衡性：Splay树倾向于保持平衡。每次操作（如插入或查找）后，最近访问的节点会被移动到树的根部，这样可以优化后续操作。

  • 局部性原则：Splay树具有良好的局部性特性，最近访问的节点会靠近树的根部。与访问过的节点相邻的节点也会被拉向根部，因此Splay树特别适合于访问频繁的操作。

  • 时间复杂度：对于M次操作，时间复杂度为O(M log N)，其中N是树中节点的数量。Splay树的操作具有摊销O(log n)的时间复杂度，这意味着在多次操作中，每次操作的平均时间是O(log n)。