Codeforces Round 820 (Div. 3)

Two Elevators

题面翻译

现在 Vlad 在一楼，他需要等电梯。公寓有两台电梯。第一台在 \(a\) 楼，第二台在 \(b\) 楼驶向 \(c\) 楼。（若 \(b\) \(=\) \(1\) ，Vlad 也上不了电梯）此时呼叫第一台电梯可以使电梯立刻从 \(a\) 楼下来，呼叫第二台电梯可以使电梯先上 \(c\) 楼，再下来。已知他们速度均为每秒一层楼，求哪辆电梯来得快。

【输入格式】

有 \(t\) 组数据，每组有 \(a\) \(b\) \(c\) 三个变量（数据 \(\le\) \(10^{8}\)）

【输出格式】

共 \(t\) 行，每行输出 \(1\) \(2\) \(3\) 中的一个，\(1\) 代表第一个电梯较快，\(2\) 代表第二个电梯较快，\(3\) 代表两个电梯一样快。

题目描述

Vlad went into his appartment house entrance, now he is on the $ 1 $ -th floor. He was going to call the elevator to go up to his apartment.

There are only two elevators in his house. Vlad knows for sure that:

  • the first elevator is currently on the floor $ a $ (it is currently motionless),
  • the second elevator is located on floor $ b $ and goes to floor $ c $ ( $ b c $ ). Please note, if $ b=1 $ , then the elevator is already leaving the floor $ 1 $ and Vlad does not have time to enter it.

If you call the first elevator, it will immediately start to go to the floor $ 1 $ . If you call the second one, then first it will reach the floor $ c $ and only then it will go to the floor $ 1 $ . It takes $ |x - y| $ seconds for each elevator to move from floor $ x $ to floor $ y $ .

Vlad wants to call an elevator that will come to him faster. Help him choose such an elevator.

输入格式

The first line of the input contains the only $ t $ ( $ 1 t ^4 $ ) — the number of test cases.

This is followed by $ t $ lines, three integers each $ a $ , $ b $ and $ c $ ( $ 1 a, b, c ^8 $ , $ b c $ ) — floor numbers described in the statement.

输出格式

Output $ t $ numbers, each of which is the answer to the corresponding test case. As an answer, output:

  • $ 1 $ , if it is better to call the first elevator;
  • $ 2 $ , if it is better to call the second one;
  • $ 3 $ , if it doesn't matter which elevator to call (both elevators will arrive in the same time).

样例 #1

样例输入 #1

1
2
3
4
3
1 2 3
3 1 2
3 2 1

样例输出 #1

1
2
3
1
3
2

提示

In the first test case of the example, the first elevator is already on the floor of $ 1 $ .

In the second test case of the example, when called, the elevators would move as follows:

  • At the time of the call, the first elevator is on the floor of $ 3 $ , and the second one is on the floor of $ 1 $ , but is already going to another floor;
  • in $ 1 $ second after the call, the first elevator would be on the floor $ 2 $ , the second one would also reach the floor $ 2 $ and now can go to the floor $ 1 $ ;
  • in $ 2 $ seconds, any elevator would reach the floor $ 1 $ .

In the third test case of the example, the first elevator will arrive in $ 2 $ seconds, and the second in $ 1 $ .

直接计算即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <bits/stdc++.h>
 
using namespace std;
 
int main() 
{
	int t;cin>>t;
	while (t--)
	{
		int a,b,c;cin>>a>>b>>c;
		int ta=a-1;//计算出a楼到1楼的时间
		int tbc=abs(c-b)+(c-1);//计算出b楼到c楼再到1楼的时间
		if(ta>tbc) puts("2");//判断快慢
		if(tbc>ta) puts("1");//puts自带换行
		if(tbc==ta) puts("3");
	}
	return 0;
}

Decode String

题面翻译

题目大意

Polycarp将一个全小写字母的字符串 s 做了以下编码：

  1. 如果这个字符在字母表中的编号 ( 如 字符 \('a'\) 的编号为 \(1\)，字符 \('z'\) 为 \(26\) ) 为个位数 \((< 10)\)，则直接输出其编号；
  2. 如果这个字符在字母表中的编号为两位数 \((\geqslant 10)\)，则在输出他的编号的基础上在其之后再输出一个 \(0\)。

现给出编码后的字符串 \(t\) ，请求出他对应的原串。

输入格式

第一行一个整数 \(q \; (1 \leqslant q \leqslant 10^4)\) 表示测试样例组数。

对于每组测试样例，第一行一个整数 \(n \; (1 \leqslant n \leqslant 50)\) 表示编码后的字符串长度。

第二行包含一个字符串 \(t\) 表示编码后的字符串。

输出格式

对于每组测试样例，输出一行一个字符串 \(s\) 表示原串

\(Translated \; by \; Zigh\)

题目描述

Polycarp has a string $ s $ consisting of lowercase Latin letters.

He encodes it using the following algorithm.

He goes through the letters of the string $ s $ from left to right and for each letter Polycarp considers its number in the alphabet:

  • if the letter number is single-digit number (less than $ 10 $ ), then just writes it out;
  • if the letter number is a two-digit number (greater than or equal to $ 10 $ ), then it writes it out and adds the number 0 after.

For example, if the string $ s $ is code, then Polycarp will encode this string as follows:

  • 'c' — is the $ 3 $ -rd letter of the alphabet. Consequently, Polycarp adds 3 to the code (the code becomes equal to 3);
  • 'o' — is the $ 15 $ -th letter of the alphabet. Consequently, Polycarp adds 15 to the code and also 0 (the code becomes 3150);
  • 'd' — is the $ 4 $ -th letter of the alphabet. Consequently, Polycarp adds 4 to the code (the code becomes 31504);
  • 'e' — is the $ 5 $ -th letter of the alphabet. Therefore, Polycarp adds 5 to the code (the code becomes 315045).

Thus, code of string code is 315045.

You are given a string $ t $ resulting from encoding the string $ s $ . Your task is to decode it (get the original string $ s $ by $ t $ ).

输入格式

The first line of the input contains an integer $ q $ ( $ 1 q ^4 $ ) — the number of test cases in the input.

The descriptions of the test cases follow.

The first line of description of each test case contains one integer $ n $ ( $ 1 n $ ) — the length of the given code.

The second line of the description of each test case contains a string $ t $ of length $ n $ — the given code. It is guaranteed that there exists such a string of lowercase Latin letters, as a result of encoding which the string $ t $ is obtained.

输出格式

For each test case output the required string $ s $ — the string that gives string $ t $ as the result of encoding. It is guaranteed that such a string always exists. It can be shown that such a string is always unique.

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
9
6
315045
4
1100
7
1213121
6
120120
18
315045615018035190
7
1111110
7
1111100
5
11111
4
2606

样例输出 #1

1
2
3
4
5
6
7
8
9
code
aj
abacaba
ll
codeforces
aaaak
aaaaj
aaaaa
zf

提示

The first test case is explained above.

In the second test case, the answer is aj. Indeed, the number of the letter a is equal to $ 1 $ , so 1 will be appended to the code. The number of the letter j is $ 10 $ , so 100 will be appended to the code. The resulting code is 1100.

There are no zeros in the third test case, which means that the numbers of all letters are less than $ 10 $ and are encoded as one digit. The original string is abacaba.

In the fourth test case, the string $ s $ is equal to ll. The letter l has the number $ 12 $ and is encoded as 120. So ll is indeed 120120.

从后往前枚举即可

遇到0的话就直接取前面两位数即可

不然的话就取一位数

注意最后翻转

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <bits/stdc++.h>

using namespace std;

int T;

int main () {
	cin >> T;
	while (T --) {
		int n;
		string s;
		cin >> n;
		cin >> s;
		string ans = "";
		int i = s.size () - 1;
		while (i >= 0) {
			if (s[i] == '0' && i - 2 >= 0) {//与前面是两位数 
				ans += 'a' + (s[i - 1] - '0') + (s[i - 2] - '0') * 10 - 1;//转化为字母 
				i = i - 3;//结束这个两位数 
			}
			else {
				ans += 'a' + (s[i] - '0') - 1;//直接添加 
				i --;
			}
		}
		reverse (ans.begin (), ans.end ());//颠倒答案字符串 
		cout << ans << endl;
	}

	return 0;
}

Jumping on Tiles

题面翻译

题目大意

给定一个字符串 \(s\)，polycarp 欲从字符串首跳到字符串末 (\(s_1\) → \(s_n\)，其中 \(n\) 表示该字符串长度)。

假设 polycarp 现从 \(a_i\) 跳到了 \(a_j\) 我们定义这一次跳跃的权值为 \(|\operatorname{index}(a_i) - \operatorname{index}(a_j)|\)，其中 \(\operatorname{index}\) 表示该字符在字母表中的序号 ( 如 \(\operatorname{index}('a') = 1, \; \operatorname{index}('z') = 26\) )。

请构造出一种在保证权值和最小的情况下经过的字符最多的跳跃方案 ( 当然，同一个字符只能经过一次，其中同一个仅指在字符串中的位置相同 )。

### 输入格式

第一行包含一个整数 \(t \; (1 \leqslant t \leqslant 10^4)\) ，表示测试样例组数。

对于每组测试样例，包含一行一个字符串 \(s \; (2 \leqslant |s| \leqslant 2 \cdot 10^5)\)，意义见题面。

### 输出格式

对于每组测试样例，第一行包含两个用空格隔开的整数 \(cost\) 和 \(m\) 分别表示 最小权值和 和 最大经过的字符数。

第二行包含 \(m\) 个整数，分别表示沿途经过的所有字符位置。( 例如输出 \(1 \; 4 \; 3 \; 5\) 表示跳跃路径为 \(s_1\) → \(s_4\) → \(s_3\) → \(s_5\) ) 数与数之间用空格隔开。

\(Translated \; by \; Zigh\)

题目描述

Polycarp was given a row of tiles. Each tile contains one lowercase letter of the Latin alphabet. The entire sequence of tiles forms the string $ s $ .

In other words, you are given a string $ s $ consisting of lowercase Latin letters.

Initially, Polycarp is on the first tile of the row and wants to get to the last tile by jumping on the tiles. Jumping from $ i $ -th tile to $ j $ -th tile has a cost equal to $ |index(s_i) - index(s_j)| $ , where $ index(c) $ is the index of the letter $ c $ in the alphabet (for example, $ index( $ 'a' $ )=1 $ , $ index( $ 'b' $ )=2 $ , ..., $ index( $ 'z' $ )=26 $ ) .

Polycarp wants to get to the $ n $ -th tile for the minimum total cost, but at the same time make maximum number of jumps.

In other words, among all possible ways to get to the last tile for the minimum total cost, he will choose the one with the maximum number of jumps.

Polycarp can visit each tile at most once.

Polycarp asks you to help — print the sequence of indices of string $ s $ on which he should jump.

输入格式

The first line of the input contains an integer $ t $ ( $ 1 t ^4 $ ) — the number of test cases in the test.

Each test case is given by the string $ s $ ( $ 2 |s| ^5 $ ), where $ |s| $ — is the length of string $ s $ . The string $ s $ consists of lowercase Latin letters.

It is guaranteed that the sum of string lengths $ s $ over all test cases does not exceed $ 2 ^5 $ .

输出格式

The answer to each test case consists of two lines.

In the first line print two integers $ cost $ , $ m $ , where $ cost $ is the minimum total cost of the path, and $ m $ is the maximum number of visited tiles Polycarp can make to get to $ n $ -th tiles for the minimum total cost $ cost $ (i.e. the number of jumps is $ m-1 $ ).

In the next line print $ m $ different numbers $ j_1, j_2, , j_m $ ( $ 1 j_i |s| $ ) — the sequence of indices of the tiles Polycarp will jump on. The first number in the sequence must be $ 1 $ (that is, $ j_1=1 $ ) and the last number must be the value of $ |s| $ (that is, $ j_m=|s| $ ).

If there are multiple answers, print any of them.

样例 #1

样例输入 #1

1
2
3
4
5
6
7
6
logic
codeforces
bca
aaaaaaaaaaa
adbaadabad
to

样例输出 #1

1
2
3
4
5
6
7
8
9
10
11
12
9 4
1 4 3 5
16 10
1 8 3 4 9 5 2 6 7 10
1 2
1 3
0 11
1 8 10 4 3 5 7 2 9 6 11
3 10
1 9 5 4 7 3 8 6 2 10
5 2
1 2

提示

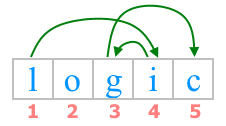
In the first test case, the required path corresponds to the picture:

In this case, the minimum possible total cost of the path is achieved. Since $ index( $ 'l' $ )=12 $ , $ index( $ 'o' $ )=15 $ , $ index( $ 'g' $ )=7 $ , $ index( $ 'i' $ )=9 $ , $ index( $ 'c' $ )=3 $ , then the total cost of the path is $ |12-9|+|9-7|+|7-3|=3+2+4=9 $ .

如果首大，就逆序排序，一直跳

不然就是正序排序，一直跳

记录下标即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <bits/stdc++.h>
#define ll long long
 
using namespace std;
 
 
bool solve() {
    string s;
    cin >> s;
    int n = s.length();
    s = "?" + s;
    vector<vector<int>> v(26);
    for (int i = 1;i <= n;i++) {
        v[s[i] - 'a'].push_back(i);
    }
    int x = s[1] - 'a', y = s[n] - 'a';
    if (x < y) 
    {
        int cnt = 0;
        for (int i = x;i <= y;i++) {
            cnt += v[i].size();
        }
        cout << abs(s[n] - s[1]) << ' ' << cnt << '\n';
        for (int i = x;i <= y;i++)
            for (auto j : v[i]) cout << j << ' ';
    }
    else {
        int cnt = 0;
        for (int i = x;i >= y;i--) {
            cnt += v[i].size();
        }
        cout << abs(s[n] - s[1]) << ' ' << cnt << '\n';
        for (int i = x;i >= y;i--)
            for (auto j : v[i]) cout << j << ' ';
    }
    cout << '\n';
    return true;
}
 
int main() {
    std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--) {
        if (!solve()) cout << -1 << '\n';
    }
    return 0;
}

Friends and the Restaurant

题面翻译

给出长度为 \(n\) 的数组 \(x\) 和 \(y\)，你可以从中选出一些数，且将这些数分为若干组，求最大组数满足每组的数量至少为 \(2\) 且每组中 \(x\) 的总和不大于 \(y\) 的总和。

By BotDand

题目描述

A group of $ n $ friends decide to go to a restaurant. Each of the friends plans to order meals for $ x_i $ burles and has a total of $ y_i $ burles ( $ 1 i n $ ).

The friends decide to split their visit to the restaurant into several days. Each day, some group of at least two friends goes to the restaurant. Each of the friends visits the restaurant no more than once (that is, these groups do not intersect). These groups must satisfy the condition that the total budget of each group must be not less than the amount of burles that the friends in the group are going to spend at the restaurant. In other words, the sum of all $ x_i $ values in the group must not exceed the sum of $ y_i $ values in the group.

What is the maximum number of days friends can visit the restaurant?

For example, let there be $ n = 6 $ friends for whom $ x $ = [ $ 8, 3, 9, 2, 4, 5 $ ] and $ y $ = [ $ 5, 3, 1, 4, 5, 10 $ ]. Then:

  • first and sixth friends can go to the restaurant on the first day. They will spend $ 8+5=13 $ burles at the restaurant, and their total budget is $ 5+10=15 $ burles. Since $ 15 $ , they can actually form a group.
  • friends with indices $ 2, 4, 5 $ can form a second group. They will spend $ 3+2+4=9 $ burles at the restaurant, and their total budget will be $ 3+4+5=12 $ burles ( $ 12 $ ).

It can be shown that they will not be able to form more groups so that each group has at least two friends and each group can pay the bill.

So, the maximum number of groups the friends can split into is $ 2 $ . Friends will visit the restaurant for a maximum of two days. Note that the $ 3 $ -rd friend will not visit the restaurant at all.

Output the maximum number of days the friends can visit the restaurant for given $ n $ , $ x $ and $ y $ .

输入格式

The first line of the input contains an integer $ t $ ( $ 1 t ^4 $ ) — the number of test cases in the test.

The descriptions of the test cases follow.

The first line of each test case contains a single integer $ n $ ( $ 2 n ^5 $ ) — the number of friends.

The second line of each test case contains exactly $ n $ integers $ x_1, x_2, , x_n $ ( $ 1 x_i ^9 $ ). The value of $ x_i $ corresponds to the number of burles that the friend numbered $ i $ plans to spend at the restaurant.

The third line of each test case contains exactly $ n $ integers $ y_1, y_2, , y_n $ ( $ 1 y_i ^9 $ ). The value $ y_i $ corresponds to the number of burles that the friend numbered $ i $ has.

It is guaranteed that the sum of $ n $ values over all test cases does not exceed $ 10^5 $ .

输出格式

For each test case, print the maximum number of days to visit the restaurant. If friends cannot form even one group to visit the restaurant, print 0.

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
6
6
8 3 9 2 4 5
5 3 1 4 5 10
4
1 2 3 4
1 1 2 2
3
2 3 7
1 3 10
6
2 3 6 9 5 7
3 2 7 10 6 10
6
5 4 2 1 8 100
1 1 1 1 1 200
6
1 4 1 2 4 2
1 3 3 2 3 4

样例输出 #1

1
2
3
4
5
6
2
0
1
3
1
3

提示

The first test case in explained in the problem statement.

In the second test case, friends cannot form at least one group of two or more people.

In the third test case, one way to visit the restaurant in one day is to go in a group of all three friends ( $ 1+3+10 +3+7 $ ). Note that they do not have the option of splitting into two groups.

两个数组可以变成一个

然后求解大于0的部分

如果最大的和最小的两个人一组就可以最大化分组数量，不然就跳过最小的数量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <bits/stdc++.h>
#define ll long long
 
using namespace std;
 
int diff[100007];
bool solve() {
    int n;
    cin >> n;
    for (int i = 1;i <= n;i++) cin >> diff[i];
    for (int i = 1;i <= n;i++) {
        int y;
        cin >> y;
        diff[i] = y - diff[i];
    }
    sort(diff + 1, diff + n + 1);
    int ans = 0;
    int l = 1, r = n;
    while (l < r) {
        if (diff[l] + diff[r] >= 0) ans++, r--;
        l++;
    }
    cout << ans << '\n';
    return true;
}
 
int main() {
    std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--) {
        if (!solve()) cout << -1 << '\n';
    }
    return 0;
}

Guess the Cycle Size

题面翻译

题意简述

现有一个有 \(n\) 个结点的无向图,这个图是一个循环图(圈状)：这个循环图的边数恰好是 \(n\) ,这个图的点从 \(1\) 到 \(n\)编号 ,点的顺序是任意的.你可以以这种方式

\(?\) \(a\) \(b\)

以询问 \(a\) 和 \(b\) 之间的距离,如果 \(a\) 或者 \(b\) 超过了 \(n\) ,则给你返回\(-1\),给你最多50次询问机会,你需要以如下方式

\(!\) \(n\)

回答你判断的图中点的个数 注意 , \(?\) \(a\) \(b\) 与 \(?\) \(b\) \(a\) 的值可能不同.交互器会以相同的概率选择两个顶点之间路径之一. 图中的顶点是随机放置的,点的位置是固定的

数据范围

\(1\leq a,b\leq10^{18} , 3\leq n\leq10^{18}\)

题目描述

This is an interactive problem.

I want to play a game with you...

We hid from you a cyclic graph of $ n $ vertices ( $ 3 n ^{18} $ ). A cyclic graph is an undirected graph of $ n $ vertices that form one cycle. Each vertex belongs to the cycle, i.e. the length of the cycle (the number of edges in it) is exactly $ n $ . The order of the vertices in the cycle is arbitrary.

You can make queries in the following way:

  • "? a b" where $ 1 a, b ^{18} $ and $ a b $ . In response to the query, the interactor outputs on a separate line the length of random of two paths from vertex $ a $ to vertex $ b $ , or -1 if $ (a, b) > n $ . The interactor chooses one of the two paths with equal probability. The length of the path —is the number of edges in it.

You win if you guess the number of vertices in the hidden graph (number $ n $ ) by making no more than $ 50 $ queries.

Note that the interactor is implemented in such a way that for any ordered pair $ (a, b) $ , it always returns the same value for query "? a b", no matter how many such queries. Note that the "? b a" query may be answered differently by the interactor.

The vertices in the graph are randomly placed, and their positions are fixed in advance.

Hacks are forbidden in this problem. The number of tests the jury has is $ 50 $ .

输入格式

输出格式

You can make no more than $ 50 $ of queries. To make a query, output on a separate line:

  • "? a b", where $ 1 a, b ^{18} $ and $ a b $ . In response to the query, the interactor will output on a separate line the length of a random simple path from vertex $ a $ to vertex $ b $ (not to be confused with the path from $ b $ to $ a $ ), or $ -1 $ if $ (a, b) > n $ . The interactor chooses one of the two paths with equal probability.

If your program gets a number 0 as a result of a query, it means that the verdict for your solution is already defined as "wrong answer" (for example, you made more than $ 50 $ queries or made an invalid query). In this case, your program should terminate immediately. Otherwise, in this scenario you may get a random verdict "Execution error", "Exceeded time limit" or some other verdict instead of "Wrong answer".

The answer, like queries, print on a separate line. The output of the answer is not counted as a query when counting them. To print it, use the following format:

  • "! n": the expected size of the hidden graph ( $ 3 n ^{18} $ ).

After that, your program should terminate.

After the output of the next query, be sure to use stream cleaning functions so that some of your output is not left in some buffer. For example, in C++ you should use function flush(stdout), in Java call System.out.flush(), in Pascal flush(output) and stdout.flush() for Python.

Note that the interactor is implemented in such a way that for any ordered pair $ (a, b) $ , it always returns the same value for query "? a b", no matter how many such queries. Note that the "? b a" query may be answered differently by the interactor.

The vertices in the graph are randomly placed, and their positions are fixed in advance.

Hacks are forbidden in this problem. The number of tests the jury has is $ 50 $ .

样例 #1

样例输入 #1

1
2
3
4
5
1

2

-1

样例输出 #1

1
2
3
4
5
6
7
? 1 2

? 1 3

? 1 4

! 3

提示

In the first example, the graph could look like this

The lengths of the simple paths between all pairs of vertices in this case are $ 1 $ or $ 2 $ .

  • The first query finds out that one of the simple paths from vertex $ 1 $ to vertex $ 2 $ has a length of $ 1 $ .

  • With the second query, we find out that one of the simple paths from vertex $ 1 $ to vertex $ 3 $ has length $ 2 $ .

  • In the third query, we find out that vertex $ 4 $ is not in the graph. Consequently, the size of the graph is $ 3 $ .

    可以发现，对任意两个点a,b，我们查询（a,b）与（b,a），只要返回的数值不同，就能确定长度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <bits/stdc++.h>
#define ll long long
 
using namespace std;
 
ll query(ll a, ll b) 
{
    cout << "? " << a << ' ' << b << endl;
    ll ans;
    cin >> ans;
    return ans;
} 
void answer(ll x) 
{
    cout << "! " << x << endl;
    exit(0);
} 
int main() {
    std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    for (int i = 2;i;i++) {
        ll ans1 = query(1, i);
        if (ans1==-1) answer(i - 1);
        ll ans2 = query(i, 1);
        if (ans1 != ans2) 
            answer(ans1 + ans2);
    }
    return 0;
}