Lec8 Disjoint Set Class

欢迎来到并查集，被称为最简洁好用的数据结构。😎

等价关系（Equivalence Relations）

等价关系的定义

  • 关系 \(R\) 定义在集合 \(S\) 上，意味着对于集合 \(S\) 中的任意一对元素 \(a, b \in S\)，\(a \, R \, b\) 要么为真，要么为假。

等价关系的三大性质

一个关系 \(R\) 是等价关系，当且仅当它满足以下三条性质：

  1. 自反性（Reflexive）：对于所有的 \(a \in S\)，都有 \(a \, R \, a\)。
  2. 对称性（Symmetric）：如果 \(a \, R \, b\)，那么 \(b \, R \, a\)，对于所有 \(a, b \in S\)。
  3. 传递性（Transitive）：如果 \(a \, R \, b\) 且 \(b \, R \, c\)，则有 \(a \, R \, c\)，对于所有 \(a, b, c \in S\)。

等价关系的示例

  • “≤” 和 “≥” 并不是等价关系，因为它们不满足对称性。
  • “=（等于）” 是等价关系，因为它满足自反性、对称性和传递性。
  • “属于同一类” 和 “电连接性” 是等价关系，因为它们满足上述三条性质。

等价类（Equivalence Class）

  • 等价类：给定一个元素 \(a \in S\)，它的等价类是集合 \(S\) 中所有与 \(a\) 有关系的元素的子集。

  • 等价类的性质：

    • \(S\) 中不同的等价类是不相交的。image-20241120142715471

    • 每个元素 \(a \in S\) 都恰好属于一个等价类。

等价问题（Equivalence Problem）

  • 问题描述：给定一个等价关系 \(R\)，决定集合 \(S\) 中一对元素 \(a, b \in S\) 是否满足 \(a \, R \, b\)，即它们是否属于同一个等价类。
  • 解决方案：可以通过检查 \(a\) 和 \(b\) 是否在同一个等价类来判断它们是否有关联。

动态等价问题（Dynamic Equivalence Problem）

问题描述

  • 策略：
    • 从每个元素的单元素集合开始，这些单元素集合是不相交的。
    • 进行两种操作：
      1. Find：查找给定元素的等价类（集合）。
      2. Union：合并两个集合。
    • 这是一个动态（在线）问题，因为集合会在操作过程中发生变化，而 Find 操作必须能够应对这些变化。

不相交集的并查集（Disjoint Union/Find）

  • 目标：实现对集合的查找（Find）和合并（Union）操作。

两种策略实现 Find 和 Union

  1. 优化 Find 操作：确保 Find 操作在最坏情况下的时间复杂度为常数时间（即 O(1)）。这通常通过路径压缩（Path Compression）技术实现。路径压缩可以减少树的深度，从而加速后续的查找操作。

  2. 优化 Union 操作：确保 Union 操作在最坏情况下的时间复杂度为常数时间（即 O(1)）。这通常通过按秩合并（Union by Rank 或 Union by Size）来实现，按秩合并总是将较小的树合并到较大的树下，从而避免树的深度过大。

约束

  • 不可能同时优化 Find 和 Union 操作的时间复杂度：在实际应用中，无法同时保证 Find 和 Union 操作都在常数时间内完成。通常是通过优化其中一个操作，而另一个操作的时间复杂度会有所妥协。

Up-Tree for D-U/F（并查集的树结构表示）

1. Up-Tree 结构介绍

  • 并查集（Disjoint Set Union/Find，简称 D-U/F）利用树形结构表示每个集合，每个元素通过父链接（parent link）指向其父节点。
  • 如果元素是根节点，则该元素的父节点值为 -1。
image-20241120143355151

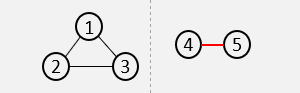
2. 树结构示例

  • 初始状态（森林）：每个元素都是一个独立的集合，根节点指向自己（父链接为 -1）。
  • 中间状态：通过合并操作（union），集合之间会形成树状结构，根节点指向其他元素，元素之间通过父链接连接。

3. 操作介绍

  • Find(x)：从元素 x 开始，沿着父链接一直查找，直到找到根节点。返回根节点即为该元素所在的集合。(Find(x) follow x to the root and return the root )
image-20241120143603587
  • Union(i, j)：假设元素 i 和 j 是两个集合的根节点，通过将 j 的根节点指向 i 来合并这两个集合。(Union(i,j) - assuming i and j roots, point j to i.)
image-20241120143636411

4. 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class DisjSets {
public:
    explicit DisjSets(int numElements);
    int find(int x) const;
    int find(int x);
    void unionSets(int root1, int root2);
private:
    vector<int> s;
};

/**
 * 构造不相交集合对象。
 * numElements 是初始的不相交集合的数量。
 */
DisjSets::DisjSets(int numElements) : s{numElements, -1} {
}

/**
 * 合并两个不相交集合。
 * 假设 root1 和 root2 是两个集合的根节点。
 * root1 是集合 1 的根节点。
 * root2 是集合 2 的根节点。
 */
void DisjSets::unionSets(int root1, int root2) {
    s[root2] = root1;  // 将 root2 的父节点指向 root1
}

/**
 * 执行查找操作。
 * 返回包含元素 x 的集合的根节点。
 */
int DisjSets::find(int x) const {
    if (s[x] < 0)
        return x;  // 如果 x 是根节点，返回 x
    else
        return find(s[x]);  // 否则，递归查找父节点
}

5. Up-Tree 的特点

  • Union 操作：每次合并两个集合时，都是将其中一个集合的根节点指向另一个集合的根节点，从而使得树的高度增加。
  • Find 操作：查找操作从一个元素开始，通过递归的方式逐层向上查找父节点，直到找到根节点。

6. 复杂度分析

  • Union 操作：在最坏情况下，Union 操作的时间复杂度为 O(1)，因为每次合并只是简单地将一个根指向另一个根。
  • Find 操作：查找操作的时间复杂度可能较高，但通过优化（如路径压缩），可以将其优化为接近常数时间。

坏情况与加权并查集优化

1. 坏情况示例

  • Union(2, 1)
  • Union(3, 2)
  • Union(n, n-1)
  • Find(1) —— 需要 n 步。

这表明在最坏情况下，如果每次都进行简单的合并操作（不做优化），查找一个元素的操作可能需要遍历整棵树，从而导致时间复杂度为 O(n)，即 n 步操作。

image-20241120144221700

2. 加权并查集（Weighted Union）

  • 加权并查集：为了避免树的高度过大，我们可以采用按树的大小（节点数）加权来合并集合。即每次合并时，总是将较小的树合并到较大的树下面，从而保持树的平衡。
  • Union-by-Size（按大小合并）：始终将较小的树连接到较大的树上，这样能有效减少树的高度。
image-20241120144241254

3. 加权并查集的性质

  • 加权并查集的树高度（h）与树的权重（n）之间的关系：
    • 一个加权并查集的上树（Up-Tree）高度为 h 时，它的权重至少为 \(2^h\)。
    • 证明：通过归纳法证明该关系。
      • 基础情况：当高度 h = 0 时，上树只有一个节点，权重为 \(2^0 = 1\)，符合条件。
      • 归纳步骤：假设对于所有高度小于 h 的上树，树的权重都至少为 \(2^{h-1}\)，现在考虑一个高度为 h 的上树。最小的加权并查集树在高度为 h 时，至少需要合并两个权重为 \(2^{h-1}\) 的子树，因此其权重至少为 \(2^h\)。

4. 时间复杂度分析

  • 对于加权并查集，通过按大小合并，可以保证树的高度不会过高。具体来说，假设树的权重为 n，则其高度 h 满足：
    • \(n \geq 2^h\)
    • 通过对数转换：\(\log_2 n \geq h\)
  • Find(x) 操作的时间复杂度：在树 T 中查找元素 x 需要经过的步数与树的高度成正比，因此其时间复杂度为 O(log n)。

关于空间上的问题

image-20241120144312914
image-20241120144320138

加权并查集最坏情况分析与优化

1. 最坏情况：N/2 次加权并查集操作

  • 加权并查集（Weighted Union）的最坏情况可能发生在树的高度增长过快的情况下。假设进行的加权并查集操作数量为 \(N - 1\)，其中每次合并的操作依次将树的高度增加一倍。具体来说，可以有如下的加权操作：

    • 第一次操作：\(N/2\) 次加权并查集操作。
    • 第二次操作：\(N/4\) 次加权并查集操作。
    • …依此类推，直到 \(1\) 次加权并查集操作。
    image-20241120150025572

    如果树的深度过高，可能导致查找操作需要沿着树的路径进行多次，增加时间复杂度。

2. 树的高度与最坏情况

  • 假设有 \(N = 2^k\) 个节点，经过多次加权并查集操作后，树的高度将达到 \(k\)，即最长路径从叶节点到根节点的长度为 \(k\)。
  • 这意味着，查找操作（Find）可能需要 \(O(k) = O(\log N)\) 的时间。

3. 替代实现：按高度合并（Union-by-Height）

  • 为了避免树的高度增长过快，我们可以使用按高度合并（Union-by-Height）策略。这个策略与按大小合并（Union-by-Size）不同，按高度合并关注的是合并树时，始终将高度较小的树合并到高度较大的树中，从而确保树的高度增长较慢。

Union-by-Height 代码示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/**
 * 合并两个不相交的集合。
 * 假设 root1 和 root2 是两个不同集合的根节点。
 * root1 是集合 1 的根，root2 是集合 2 的根。
 */
void DisjSets::unionSets( int root1, int root2 )
{
    if( s[ root2 ] < s[ root1 ] ) // root2 的高度更深
        s[ root1 ] = root2; // 使 root2 成为新的根
    else {
        if( s[ root1 ] == s[ root2 ] )
            --s[ root1 ]; // 如果高度相同，更新高度（注意：高度是负数）
        s[ root2 ] = root1; // 使 root1 成为新的根
    }
}

4. 按高度合并的效果

  • 在按高度合并的策略下，树的深度始终不会超过 $ _2 N $，从而避免了树的高度过大，确保了查找操作的时间复杂度始终维持在 $ O(N) $。
  • 树的深度：每次合并时，较低的树将被附加到较高的树上，这保证了树的高度始终保持在 $ O(N) $ 级别，从而避免了最坏情况的发生。

5. 总结

  • 使用加权并查集（无论是按大小合并还是按高度合并）都能有效减少树的高度，从而提高查找操作的效率。
  • 按高度合并（Union-by-Height）策略比简单的加权并查集（按树的大小合并）在实际应用中更常用，因为它保证了树的高度始终保持较小，进一步优化了查找操作的时间复杂度。
  • 最坏情况发生时，即使经过多次合并操作，树的高度也只会是 $ O(N) $，从而避免了树的深度过大导致查找效率低下的问题。

路径压缩（Path Compression）与加权并查集（Weighted Union）结合的优化

1. 路径压缩 (Path Compression) 的原理

  • 目标：在执行 Find 操作时，将查找路径上的所有节点直接指向树的根节点，从而扁平化树的结构，减少后续查找操作的路径长度。
  • 实现：通过递归实现路径压缩，在返回根节点的同时更新路径上的每个节点，使它们直接指向根节点。

路径压缩的代码实现

1
2
3
4
5
6
7
8
9
10
11
/**
 * 执行带路径压缩的 Find 操作。
 * 查找并返回包含元素 x 的集合的根。
 */
int DisjSets::find( int x )
{
    if( s[ x ] < 0 )
        return x; // 如果 x 是根节点，直接返回
    else
        return s[ x ] = find( s[ x ] ); // 路径压缩，将 x 直接连接到根
}
  • 如果节点 \(x\) 不是根节点，递归调用 find(s[x]) 查找根节点，并将路径上的所有节点直接连接到根节点。

2. 加权并查集与路径压缩结合的优化

  • 加权并查集 (Weighted Union)：
    • 将节点较少的树合并到节点较多的树上，减少树的高度。
    • 保证合并操作的最坏时间复杂度为 \(O(1)\)。
  • 路径压缩 (Path Compression)：
    • 在每次查找操作中扁平化树的结构，降低后续操作的路径长度。
    • 查找操作的最坏时间复杂度为 \(O(\log N)\)。
  • 结合后的特点：
    • 单次操作的时间复杂度可能较高，但 m 次操作的总时间复杂度为 \(O(m \cdot \log^* N)\)。
    • \(\log^* N\) 是一个增长极其缓慢的函数，在实际应用中，几乎是常量时间。

3. \(\log^* N\) 的定义与意义

  • \(\log^* N\) 是迭代对数函数，表示在对数操作下，达到 1 所需的最少迭代次数：
    • \(\log^* 2 = 1\)
    • \(\log^* 4 = 2\) （因为 \(\log_2(4) = 2\)）
    • \(\log^* 16 = 3\) （因为 \(\log_2(16) = 4 \rightarrow \log_2(4) = 2 \rightarrow \log_2(2) = 1\)）
    • \(\log^* 65536 = 4\) （因为 \(65536 = 2^{16}\)）
    • \(\log^* 2^{65536} = 5\)
  • 意义：即使对于非常大的 \(N\)，\(\log^* N\) 依然是一个很小的值，通常小于 5。

4. 性能分析

  • 最坏情况分析：
    • Find 操作：\(O(\log N)\)，因为路径压缩可能需要多次递归直到找到根节点。
    • Union 操作：\(O(1)\)，通过加权合并树可以在常数时间完成。
  • 整体时间复杂度：
    • \(m \geq N\) 次操作的总时间复杂度为 \(O(m \cdot \log^* N)\)，这对于实际应用来说可以近似看作常数时间。

5. 路径压缩与加权并查集的优点

  • 高效性：操作的平均时间复杂度接近常数。
  • 可扩展性：适用于处理动态集合问题，例如图的连通性问题。
  • 实际应用：即使面对大规模数据，结合路径压缩的加权并查集也能保持高效。